現狀數據下帶測量誤差的半參數加速風險模型的估計

摘要：基于現狀數據提出一種帶有測量誤差的半參數加速風險回歸模型.首先，用I樣條近似未知累積基線風險函數，并基于Sieve極大似然估計方法獲得模型的參數估計；其次，用模擬外推方法修正協變量的測量誤差帶來的估計誤差；再次，通過數值模擬驗證該方法的有效性以及忽略協變量誤差對估計的影響；最后將該方法應用到心腦血管病死亡率的研究中獲得心腦血管病發死亡的風險函數估計，實驗結果表明，該方法有效。

關鍵詞：加速風險模型；模擬外推；測量誤差；極大似然估計；I樣條

中圖分類號：O212文獻標志碼：A文章編號：1671-5489（2024）05-1122-07

Estimation for Semi-parametric Accelerated Hazard Model with Measurement Error under Current Status Data

PEI Yifan，ZHAOBo，WANG Chunjie

（School of Mathematics and Statistics，Changchun University of Technology，Changchun 130012，China）

Abstract：We proposed a semi-parametric accelerated hazard regression model with measurement errors based on the current status data.Firstly，the unknown baseline cumulative hazard function was approximated by using I-spline，and parameter estimates of the model were obtained based on Sieve maximum likelihood estimation method.Secondly，a simulation extrapolation method was used to correct estimation error caused by measurement errors in covariates.Thirdly，the numerical simulations were carried out to verify the effectiveness of the proposed method as well as the impact of ignoring measurement error in covariates.Finally，the proposed method was applied to study cardiovascular and cerebrovascular disease mortality，we obtained estimation of hazard function for cardiovascular and cerebrovascular disease mortality.The experimental results show that the proposed method is effective.

Keywords：accelerated hazard model;simulationextrapolation;measurementerror;maximum likelihood estimate;I-spline

僅已知個體在當前狀態下感興趣事件是否發生，確切的發生時間不能被觀測到，這時得到的數據即為現狀數據[4].例如，在對心腦血管病死亡率的研究中，病人準確的死亡時間不能被準確觀察到，只知道個體在隨訪期間內是否發生死亡，這類數據即為經典的現狀數據，在這項研究中選取6個變量對死亡率進行預測，其中血液中血小板數量和血清鈉的水平經常存在測量誤差，如果忽略測量誤差的影響可能會使估計結果存在偏差，因此針對帶有測量誤差的現狀數據建立模型并提出誤差修正方法非常必要.

近年來，關于對協變量帶有測量誤差的模型研究已有許多結果，特別是對在右刪失數據下帶測量誤差的加速失效時間模型的研究.例如：He等用模擬外推方法對參數加速失效時間模型進行了分析，并將所提出的方法應用到冠心病死亡率的研究中；Yu等[6]使用回歸校正]的方法對帶測量誤差的協變量進行修正，并將所提出的方法應用到抑郁癥死亡率的研究中；在實際應用中，隨機誤差項的分布形式通常是未知的，Zhang等在文獻[5]的基礎上將參數加速失效時間模型推廣到了半參數加速失效時間模型；Chen9]在長度偏差數據下對帶有測量誤差的加速失效時間模型進行了估計，用模擬外推方法對測量誤差進行修正，并對其理論性質進行了證明。此外，在其他模型假設下討論帶測量誤差數據的分析方法也取得了一些研究成果.例如：Cao等對協變量帶有誤差的Cox比例風險模型進行研究，使用回歸校正的方法對帶有誤差的協變量進行誤差修正；Pan等對具有時依協變量的部分線性Cox比例風險模型進行研究，使用Bayes平滑方法對帶有誤差的協變量進行修正；Ghapani等]提出了一種雙參數加權混合估計方法對線性測量誤差模型的參數進行估計，并對其理論性質進行了證明；Dong等提出了一個半參數估計方法對存在測量誤差的變系數模型進行估計.

加速風險模型是基于加速失效時間模型推廣得到的一種半參數模型[+]，因其靈活性而備受關注.在特殊情形下，該模型可退化為比例風險模型、比例優勢模型和加速失效模型.因此，本文在加速風險模型下討論協變量帶有測量誤差的現狀數據的半參數回歸分析問題，利用1樣條近似未知基準累積基線風險函數，同時引入模擬外推方法修正測量誤差導致的估計誤差，數值模擬結果驗證了所提方法的有效性.

1數據及模型

設T為個體的失效時間，C為個體的觀測時間.當T≤C時只知在C時刻已發生感興趣事件，具體的發生時間觀測不到，這時便出現了左刪失；當Tgt;C時只知在C時刻未發生感興趣事件，具體的發生時間不能準確觀測到，這時便出現了右刪失，通常這類只知個體當前所處狀態的數據稱為現狀數據.設X是受測量誤差影響的q1維協變量，Z是不受測量誤差影響的q2維協變量，δ為一個示性函數，當T≤C時，8=1，當Tgt;C時，8=0.則數據可表示為（C，8，X，Z）.

當給定協變量時，加速風險模型可表示為

其中A（·）為分布形式未知的累積基線風險函數，X和Z為觀測到的協變量，β和a為待估參數，exp{BTX+aTZ}為加速因子.當A（s）=exp{s}時，加速風險模型可退化為比例風險模型.加速風險模型的生存函數可表示為

在實際應用中的一些變量通常帶有測量誤差，本文假設帶誤差的協變量滿足經典測量誤差模型

其中W為協變量的實際觀測值，e為測量誤差，e與X和W相互獨立，E（e）=0，Var（e）=∑.

2極大似然估計

假設（C1，8，X1，Z1）是（C，8，X，Z）的第i（i=1，2，·，n）個觀測樣本，假設刪失時間C與失效時間T；相互獨立，則似然函數可通過下式給出：

將似然函數取對數，可寫為

由于A。（·）為分布形式未知的累積基線風險函數，直接對似然函數求極大值較困難，因此本文通過構建一個有限維的線性函數去逼近分布形式未知的無限維累積基線風險函數.目前常用的方法有B樣條、I樣條、M樣條、Bernstein多項式等近似方法[2]，本文根據累積基線風險函數單調非遞減的性質以及I樣條的單調性，使用文獻[21]中的1條對累積基線風險函數進行逼近，只需控制樣條系數大于0便可保證累積基線風險函數估計量的非負性和單調性，因此未知函數可近似為

其中K=m+p+1，m為樣條基函數內部節點的個數，通常取百分位點作為樣條節點的位置，p為樣條基函數的自由度.本文參考文獻[21]，選擇三次樣條（p=3），5個內部節點數（m=5），則在樣條近似的情況下可得如下對數似然：

使用極大似然估計方法對感興趣參數求解，在用極大似然估計時首先通過對感興趣參數求偏導得到得分方程，然后對得分方程求根進而得到感興趣參數的估計值.通過對似然函數求偏導得到得分方程：

其中-（）導數

對上述得分方程求根，即可得到感興趣參數a，B，y的估計值.由于協變量W；帶有測量誤差，直接對得分方程進行求根得到的參數估計值可能有偏差，因此需要選擇合適的方法對帶誤差的協變量進行誤差校正.常用的誤差校正方法有回歸校正和模擬外推兩種方法，由于本文的模型形式較復雜，因此使用模擬外推方法對誤差進行校正，分為以下3個步驟.

1）模擬步.

在該步使用重抽樣的方法對帶有測量誤差的協變量進行重新測量得到一組新的協變量，得到的新協變量與之前帶測量誤差的協變量有以下關系：

其中：隨機變量u～N（0，1），i=1，2，··，n，g=1，2，·，G，u。與觀測數據獨立同分布；h∈H={h1，··，hM}，h的取值范圍為[0，2]；G和M為給定的正整數.

2）估計步.

對于給定的h和g，用估計步得到的W（h）去代替實際觀測到的W，得到新樣本數據{C1，81，W（h），Z1}1，將得到的新樣本數據代入似然函數中，則似然函數可寫為以下形式：

其中=exp｛（h）W（h）+a（h）ZC.當h給定時，對每個g都可得到6=（B，a）的估計值，進面得到一列關于的估計值然后將所得到的信計值取均值得到（當取H中給定的數時即可得到{h，0（h），h∈H}.

3）外推步.

該步需要通過外推函數去尋求給定h與估計步中得到的估計值0（h）之間的關系，定義外推函數為f（h）=a+bh+ch2.基于給定的ん與估計出的（h）可得目標函數∑（h）-f（h）2.極小化該目標函數，即可得外推函數參數的估計值.最后根據模擬外推方法5可知，當h=-1時，即可得到修正后的參數估計值0SMEX=f（-1）.

下面討論估計的大樣本性質.設0。表示模型參數0的真值，根據文獻[5，9]中參數估計的理論性質可知，當樣本容量n→∞時，模擬外推修正后獲得的參數估計值0SIMEX具有相合性和漸近正態性，即n（sux-O）→N（0，D-1）.在實際分析中對D進行計算較復雜，因此本文采用Bootstrap抽樣方法[22]近似計算參數估計值的方差.假設{C，8，W，Z}（j=1，2，·，J）表示樣本{C，8，W，Z}中有放回抽取容量為n的樣本，參數估計值0agx（j=1，2，··，J）表示第j個樣本下獲得的模擬外推修正估計，則0SIMEX的方差可表示為

3模擬研究

下面進行數值模擬以驗證本文方法的有效性.考慮不帶誤差的協變量服從概率為0.5的二項分布B（0.5），帶有誤差的協變量X分別服從標準正態分布N（0，1），取值范圍為0～3.5的均勻分布U（0，3.5），均值為1的指數分布Exp{1}，協變量的誤差服從正態分布e～N（0，o2），e的標準差為0=0.3或a2=0.4，可靠性比由02/（02+02）給出，本文可靠性比為0.9和0.85，刪失時間C～Exp（10）.失效時間T由以下模型生成：

其中A0（s）=0.25s.δ為一個示性函數，當T≤C時δ=1，當Tgt;C時δ=0.

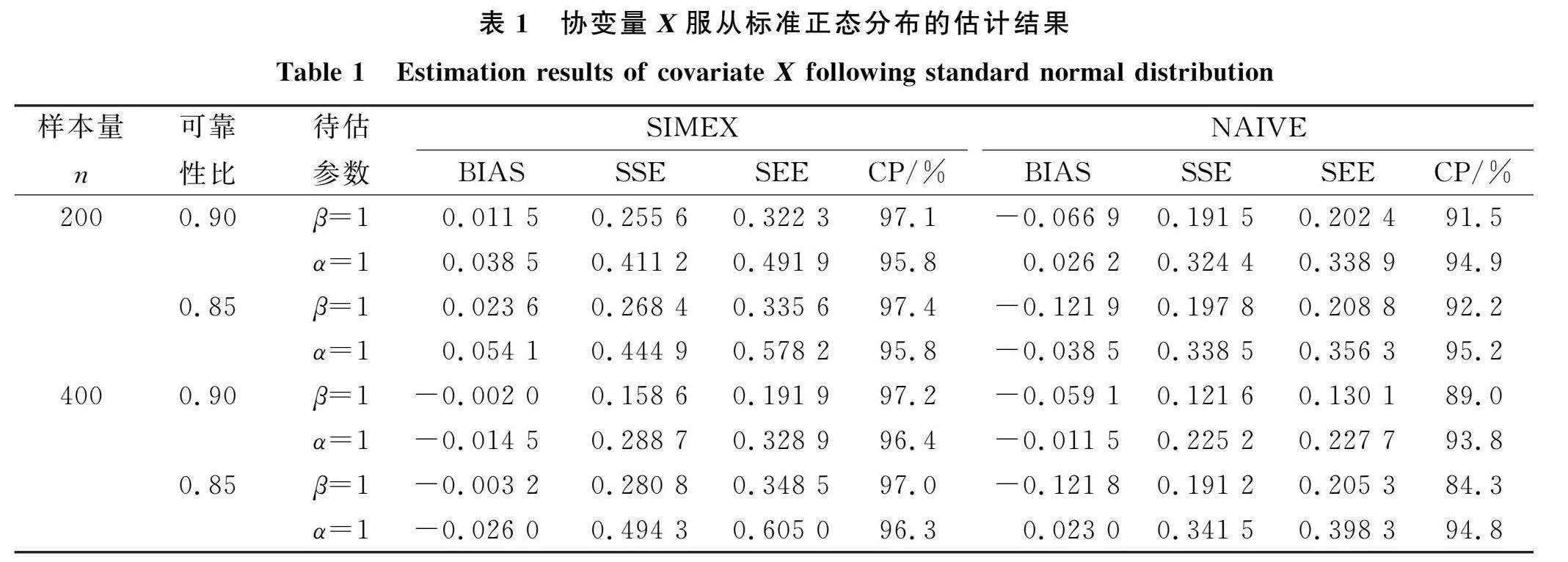
模擬計算分別產生了200個和400個獨立同分布的樣本，Bootstrap次數設為50次，并進行500次循環.在模擬外推中，G=30，M=5，H={0，0.5，1，1.5，2}，在外推步中使用二次外推函數.用NAIVE表示不考慮測量誤差的估計結果；SIMEX表示使用模擬外推的估計方法對帶有誤差的協變量進行誤差修正后的估計結果.用BIAS表示估計結果的偏差；SSE表示樣本估計值的標準差；SEE表示用Bootstrap方法得到的標準差估計的平均值；CP表示待估參數的95%經驗覆蓋率，表1為協變量X服從標準正態分布時參數的估計結果.

由表1可見，與未修正的估計結果相比，使用SIMEX方法修正后的估計結果在大多數情況下都有更小的偏差和更好的CP，且隨著樣本量的增大，估計的偏差也隨之減小，估計結果具有相合性.當增加測量誤差的幅度時，測量誤差的影響也隨之增大.

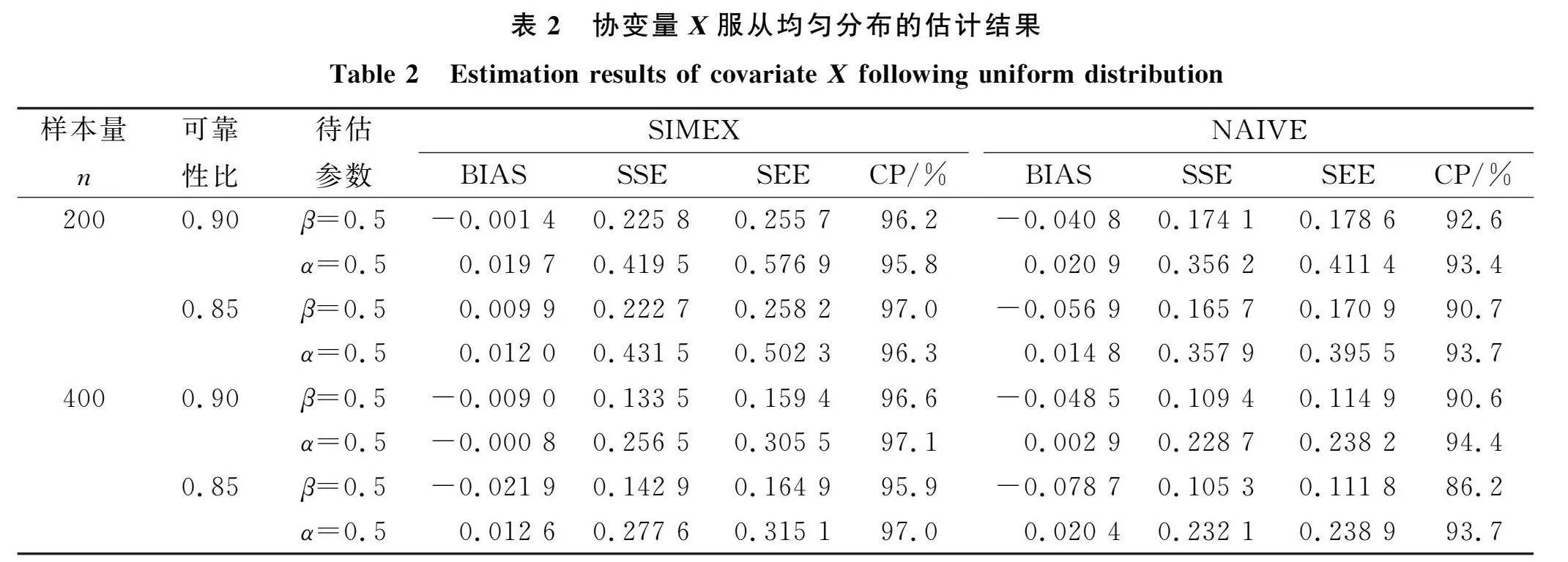
表2為協變量X服從均勻分布時參數的估計結果.由表2可見：協變量服從均勻分布和協變量服從指數分布性質相同；對帶誤差的協變量進行修正后的偏差小于沒有修正前的偏差，且隨著樣本量的增大，估計值的偏差有減小的趨勢；樣本估計值的標準差與標準差估計的平均值之間相差較小，且修正后的CP值也較好.

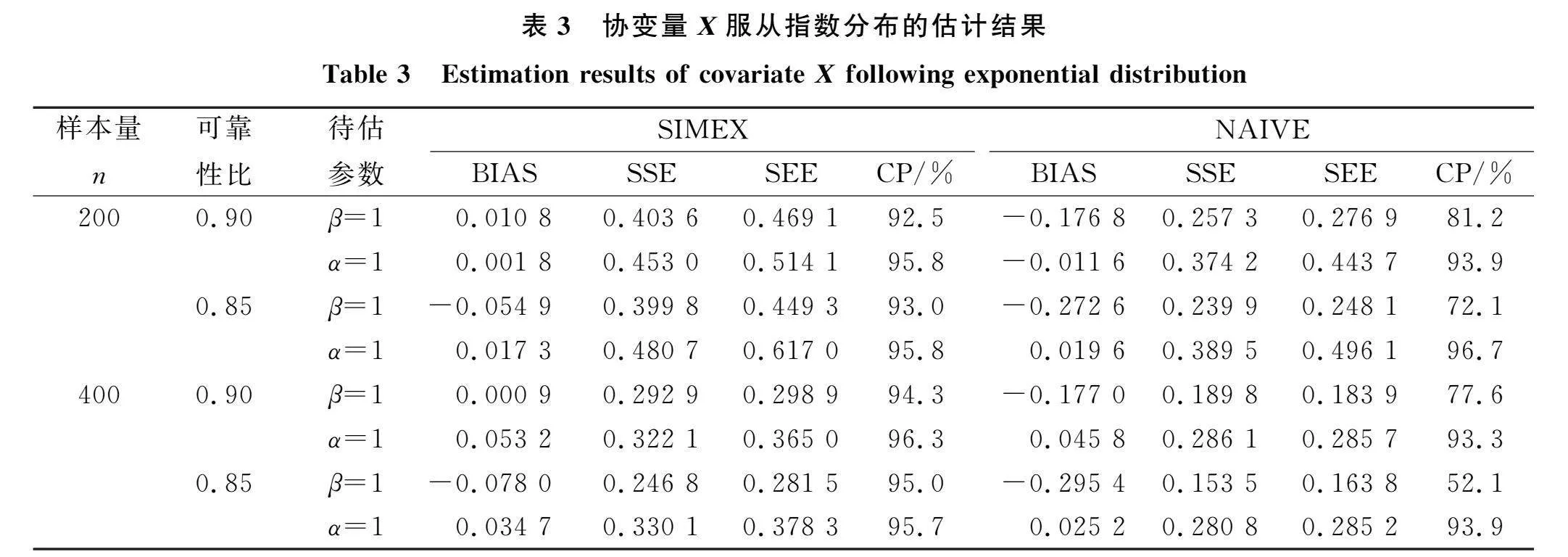
表3為協變量X服從指數分布時參數的估計結果.由表3可見：對帶誤差的協變量進行誤差修正后減少了參數估計值的偏差，與表1和表2具有相同的性質；隨著樣本量的增大，估計的偏差隨之減少，隨著誤差幅度的增大，估計的偏差也隨之增大，且修正后比修正前的CP值更接近95%.

上述模擬結果表明，協變量在不同分布形式下有相同的性質，證明了本文方法的有效性.由模擬結果可知，測量誤差對參數的估計效果有較大影響，若不對測量誤差進行修正，則估計結果將會產生巨大偏差.因此對帶有誤差的協變量進行誤差修正十分必要.

4實例分析

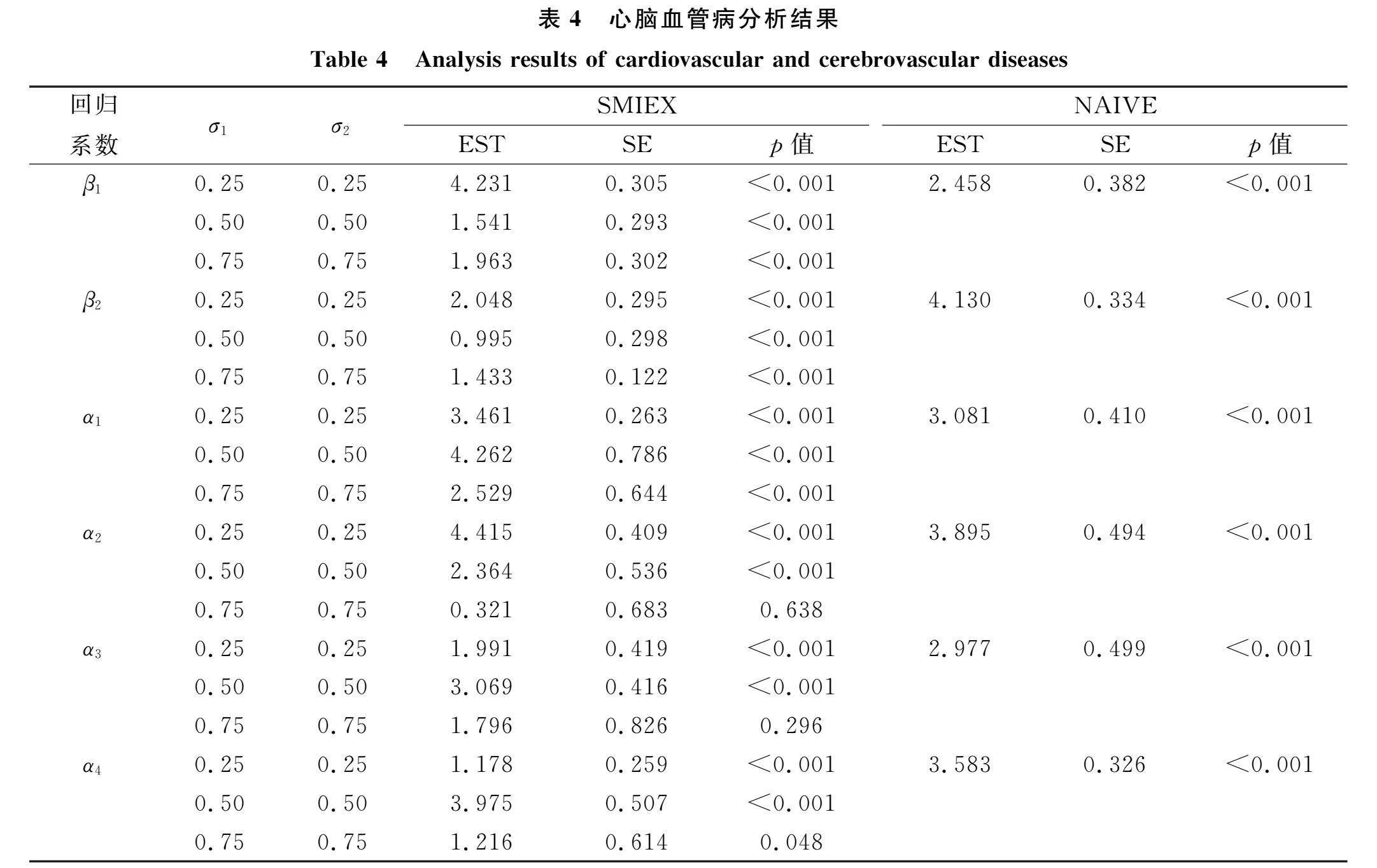
下面將本文提出的半參數加速風險模型應用于心腦血管病死亡率的研究中，所用數據集來源于巴基斯坦費薩拉巴德心臟病學研究所和費薩拉巴德聯合醫院[23].該數據集是為研究哪些指標對患心腦血管病病人的死亡率有影響，在這項研究中個體的死亡時間不能被直接觀察到，只知道個體在隨訪期間是否發生死亡，因此該數據為現狀數據.該數據集共收集了299個樣本，用6個變量對死亡時間進行預測，其中T表示死亡時間，C表示觀察時間，x1表示血液中血小板數量，x2表示血液中血清鈉水平，1表示是否有高血壓，2表示是否吸煙，3表示是否患有糖尿病，z4表示個體的性別.在血液中血小板數量和血清鈉水平的測量中，由于儀器設備的因素，常會存在一定程度的測量誤差.因此，用本文方法對帶有誤差的協變量進行誤差修正，為獲得模型的估計結果，設模擬外推常數G=30，M=5，H={0，0.5，1，1.5，2}.根據文獻[8]，將測量誤差的標準差設為o1，02=0.25，0.5，0.75.

表4列出了數據集中心腦血管病的分析結果，其中EST表示回歸系數的估計值，SE表示標準誤差，p值為檢驗回歸系數等于0的最小顯著性水平.由表4可見，當測量誤差較小時，所有變量的參數估計值均大于0且對應的p值都小于0.05，表明這些變量對心腦血管病死亡率都具有顯著性的正向影響.在一定范圍內，隨著血液中血小板數量的增加或血液中血清鈉水平的升高均會增加心腦血管病死亡的風險，因此控制血液中血小板數量和血清鈉水平有助于降低心腦血管病死亡的風險；男性患有心腦血管病的死亡率高于女性；患有高血壓、吸煙以及患有糖尿病都會增加心腦血管病死亡的風險，因此對患有心腦血管病的人群需要做到健康飲食，并進行適當的體育鍛煉，進而降低個體患高血壓和糖尿病的風險，吸煙人群也需要盡量戒煙，進而降低死亡的風險。

當測量誤差增大時，系數的估計方向與測量誤差較小時的估計方向一致，即隨著血液中血小板數量的增高或血液中血清鈉水平的升高均會增加心腦血管病死亡的風險，因此患有心腦血管病的病人需要定期到醫院進行檢查或者通過服用一些藥物將這兩個變量控制在一定范圍內，從而降低死亡的風險.男性患有心腦血管病死亡的風險高于女性.患有高血壓將會增加心腦血管病死亡的風險，因此對患有心腦血管病的人群需要關注自身血壓的情況，進而降低死亡風險.但隨著測量誤差的增大，吸煙和患有糖尿病對應的p值大于0.05，表明在實際應用中當血液中血小板數量和血液中血清鈉水平存在較大誤差時，會導致吸煙和患有糖尿病對心腦血管病死亡率的影響在統計學意義上是不顯著的，因此在實例數據分析中對帶有測量誤差的協變量進行誤差修正非常必要.

綜上所述，本文在現狀數據下，對協變量帶有測量誤差的加速風險模型進行了分析，其中隨機誤差項的分布形式未知.先使用I樣條對分布形式未知的累積基線風險函數進行逼近，再使用模擬外推方法對帶誤差的協變量進行修正，最后將本文方法應用到心腦血管病的研究中，數值模擬結果表明，使用模擬外推方法對帶誤差的變量進行修正可以減小參數估計值的偏差.

參考文獻

[1]PUNEKAR S R，VELCHETI V，NEEL.B G，etal.The Current State of the Art and Future Trends in RAS-Targeted Cancer Therapies[J].Nature Reviews Clinical Oncology，2022，19（10）：637-655.

[2]LIU T Q，YUAN X H，SUN J G.Weighted Rank Estimation of Nonparametric Transformation Models withCase-1 and Case-2 Interval-Censored Failure Time Data[J].Journal of Nonparametric Statistics，2021，33（2）：225-248.

[3]ABOUBAKAR M.KELLIL M，ROUX P.A Review of IoT Network Management：Current Status andPerspectives[J].Journal of King Saud University：Computer and Information Sciences，2022，34（7）：4163-4176.

[4]ZAWACKI-RICHTER O.The Current State and Impact of Covid-19 on Digital Higher Education in Germany[J].Human Behavior and Emerging Technologies，2021，3（1）：218-226.

[5]HE WQ，YI G Y，XIONG J.Accelerated Failure Time Models with Covariates Subject to Measurement Error[J].Statistics in Medicine，2007，26：4817-4832.

[6]YU M G，NANB.Regression Calibration in Semiparametric Accelerated Failure Time Models[J].Biometrics，2010，66（2）：405-414.

[7]WANG C Y，HSU L，FENG Z D，etal.Regression Calibration in Failure Time Regression[J].Biometrics，1997，53（1）：131-145.

[8]ZHANG J J，HE W Q，LI H F.A Semiparametric Approach for Accelerated Failure Time Models with CovariatesSubject to Measurement Error[J].Communications in Statistics：Simulation and Computation，2014，43（2）：329-341.

[9]CHEN L.P.Semiparametric Estimation for the Accelerated Failure Time Model with Length-Biased Sampling and Covariate Measurement Error[J].Stat，2018，7（1）：e209-1-e209-8.

[10]CAO Z Q，WONG M Y.Approximate Profile Likelihood Estimation for Cox Regression with Covariate Measurement Error[J].Statistics in Medicine，2022，41（5）：910-931.

[11]PAN A Q，SONG X，HUANG H W.Bayesian Analysis for Partly Linear Cox Model with Measurement Error and Time-Varying Covariate Effect[J].Statistics in Medicine，2022，41（23）：4666-4681.

[12]GHAPANI F，BABADI B.Two Parameter Weighted Mixed Estimator in Linear Measurement Error Models[J].Communications in Statistics：Simulation and Computation，2022，51（12）：6936-6946.

[13]DONG H，OTSU T，TAYLOR L.Estimation of Varying Coefficient Models with Measurement Error[J].Journal of Econometrics，2022，230（2）：388-415.

[14]LIN X Y.A Bayesian Semiparametric Accelerated Failure Time Model for Arbitrarily Censored Data with Covariates Subject to Measurement Error[J].Communications in Statistics：Simulation and Computation，2017，46（1）：747-756.

[15]SHEN J S，LI Z N，YU H J，etal.Semiparametric Bayesian Inference for Accelerated Failure Time Models with Errors-in-Covariates and Doubly Censored Data[J].Journal of Systems Science and Complexity，2017，30（5）：1189-1205.

[16]YI G Y，HE W Q.Methods for Bivariate Survival Data with Mis measured Covariates under an Accelerated Failure Time Model[J].Communications in Statistics：Theory and Methods，2006，35（7/8/9）：1539-1554.

[17]USOL'TSEVA O S.A Consistent Estimator in the Accelerated Failure Time Model with Censored Observations and Measurement Errors[J].Theory of Probability and Mathematical Statistics，2011，82：161-169.

[18]LI Y.LIANG M X，MAO L，etal.Robust Estimation and Variable Selection for the Accelerated Failure Time Model[J].Statistics in Medicine，2021，40（20）：4473-4491.

[19]DONG XX，KONG L，WAHED A S.Accelerated Failure Time Model for Case-Cohort Design with LongitudinalCovariates Subject to Measurement Error and Detection Limits[J].Statistics in Medicine，2016，35（8）：1327-1339.

[20]PERPEROGLOU A，SAUERBREI W，ABRAHAMOWICZ M，etal.A Review of Spline Function Procedures inR[J/OL].BMC Medical Research Methodology，（2019-03-06）[2024-03-10].https：//doi.org/10.1186/s12874-019-0666-3.

[21]RAMSAY J O.Monotone Regression Splines in Action[J].Statistical Science，1988，3（4）：425-441.

[22]JOHNSON R W.An Introduction to the Bootstrap[J].Teaching Statistics，2001，23（2）：49-54.

[23]CHICCO D.JURMAN G.Machine Learning Can Predict Survival of Patients with Heart Failure from Serum Creatinine and Ejection Fraction Alone[J/OL].BMC Medical Informatics and Decision Making，（2020-02-03）[2023-11-20].https：/doi.org/10.1186/s12911-020-1023-5.

（責任編輯：趙立芹）