動態多尺度決策信息系統局部最優尺度的更新規律

摘要： 在對象動態增加的情況下，對多尺度決策信息系統（MDIS）保持局部決策類不確定性的最優尺度更新規律進行研究。首先，介紹決策信息系統和多尺度決策信息系統決策類不確定性的基本知識，以及MDIS保持局部決策類不確定性的最優尺度定義。然后，在增加一個對象的條件下，分析MDIS局部決策類不確定性的更新規律。最后，采用增量學習方法，給出增加一個對象條件下MDIS局部最優尺度不變和變大的充分必要條件。結果表明：文中方法可以快速地確定更新系統局部最優尺度。

關鍵詞： 粒計算； 多尺度決策信息系統； 局部最優尺度選擇； 不確定性； 動態更新

中圖分類號： TP 18文獻標志碼： A"" 文章編號： 1000-5013（2024）06-0800-08

Updating Law of Local Optimal Scale of Dynamic Multi-Scale Decision Information System

CHEN Yingsheng1， LI Jinjin1，2

（1. School of Mathematical Sciences， Huaqiao University， Quanzhou 362021， China；

2. School of Mathematics Sciences and Statistics， Minnan Normal University， Zhangzhou 363000， China）

Abstract：

Research on the updating law of optimal scale of multi-scale decision information system （MDIS） to keep local decision class uncertainty under the condition of dynamic increase of objects. Firstly， the basic knowledge of decision class uncertainty of decision information system and multi-scale decision information system are introduced， and the definition of optimal scale of MDIS to keep local decision class uncertainty is given. Then， the updating law of local decision class uncertainty of MDIS is analyzed under the condition of adding one object. Finally， using the incremental learning method， the sufficient and necessary conditions are given for the local optimal scale of MDIS to remain invariant or increase under the condition of adding an object. The results show that the proposed method can quickly determine the local optimal scale of the update system.

Keywords：

granular computing； multi-scale decision information system； local optimal scale selection； uncertainty； dynamic update

粒計算是模仿人類思維方式的一種處理信息的計算范式［1］。隨著人工智能和信息科學的發展，粒計算已廣泛應用于人工智能、知識發現、決策分類、醫療診斷等領域， 成為進行海量數據挖掘、不確定性分析等復雜問題的強有力工具［2-5］。多粒度是粒計算的一種顯著特征，多尺度分析是處理復雜信息的一

種重要方法。Wu等［6］首先提出多尺度決策信息系統（MDIS）模型，隨后許多學者對這一模型進行大量的研究，主要包含粗糙近似與協調性的傳遞規律［7］、決策規則［8］、粗糙度和信息熵［9］、最優尺度問題［7-14］等。最優尺度是MDIS的核心問題，它研究以最小的條件信息達到最優的決策效果。Wu等［6］討論MDIS的8種協調性的最優尺度，并對其進行綜合分析和比較。She等［8］利用決策樹，引入裁剪方法，以決策規則為標準，研究最優尺度與屬性約簡同步的具體算法。Li等［9］將系統推廣到廣義多尺度決策信息系統，采用分步優化的方法設計了一種最優尺度搜索算法。Huang等［10］將該模型推廣到多尺度決策的情況下，并討論最優尺度選擇問題。陳應生等［11］構建多尺度集值信息系統，引入尺度重要度，給出系統的最優尺度選擇算法。關于局部最優尺度的研究，顧沈明等［12］，馬周明等［13］研究多尺度決策信息系統的局部最優尺度選擇問題；吳偉志等［14］ 研究不協調廣義多尺度決策系統的局部最優尺度組合選擇問題。

動態變化是大數據的一個重要特征，增量學習是處理動態數據的一種重要方法，它主要研究更新的信息而不是重新計算，從而顯著地提高效率。增量學習方法在粒計算中得到了應用，Yang等［15］提出一種動態概念更新方法；Zhang等［16］提出一個概率粗糙集的動態框架，并使用增量算法更新不確定區域；He等［17］通過矩陣的更新策略設計一種增量算法，并研究模糊概率粗糙集三支區域的更新規則。

在MDIS領域，Deng等［18］在MDIS上定義了一個模糊隸屬度，并采用三支決策理論和增量學習方法探索最優尺度；Luo等［19］研究不完全MDIS中具有動態尺度變化的三支決策更新問題。然而，這些研究知識采用增量學習方法進行尺度間的信息更新，并未考慮到由于對象或屬性的增刪引起的動態變化因素。目前，只有少量學者研究對象動態增加的情況下MDIS最優尺度的更新問題，Hao等［20］運用三支決策理論研究MDIS在對象增加時系統最優尺度的更新算法；Chen等［21］研究在對象動態增加條件下系統最優尺度減小的充要條件；Li等［22］進一步研究在增加一個對象時，系統最優尺度相等和增加的充要條件。由于在具體的應用中有時只需要考慮局部決策的問題，故Chen等［23］研究保持系統局部決策類不確定性的最優尺度更新問題。

基于此，本文對局部決策類的最優尺度問題展開研究，給出最優尺度不變和變大的充分必要條件，提出增加對象條件下最優尺度更新判斷的快捷方法。

1 基礎知識

1.1 決策信息系統決策類的不確定性

定義1［6］ S=（U，A∪g0gggggg）稱為一個決策信息系統，其中，U={x1，x2，…，xn}是一個非空有限集合，稱為論域，A={a1，a2，…，am}是一個非空有限屬性集，對于任意的a∈A，a：U→Va是一個單值映射，其中，Va={a（x）x∈U}是屬性a的值域。

dA稱為一個決策屬性，d：U→Vd是一個單值映射，其中，Vd={d（x）x∈U}是屬性d的值域。

對于任意的屬性子集BA，定義等價關系

RB={（x，y）∈U×Ua（x）=a（y），a∈B}。

［x］B={y∈Ua（x）=a（y），a∈B}為對象x關于屬性子集B的等價類。對于BA，XU，X關于屬性子集B的上下近似分別定義為

RB（X）={x∈U［x］B∩X≠}，" RB（X）={x∈U［x］BX}。

由屬性d誘導的等價關系為

Rd={（x，y）∈U×Ud（x）=d（y）}。

［x］d={y∈U（x，y）∈Rd}為x關于d的等價類，U/Rd={Rd（x）x∈U}稱為Rd的商集。

對于任意的決策類D∈U/Rd，U被分成3個互不相交的區域，即

PosB（D）=RB（D）={［x］B［x］BD，x∈U}，

NegB（D）=U-RB（D）={［x］B［x］B∩D=，x∈U}，

BndB（D）=RB（D）-RB（D）={［x］B［x］BX，［x］B∩D≠，x∈U}。

式中：PosB（D）是可以完全確定屬于D的信息粒，稱為接受域；NegB（D）是完全不屬于D的信息粒，稱為拒絕域；BndB（D）是不能確定屬于D或不屬于D的信息粒，稱為邊界域；PosB（D）與NegB（D）是完全可以決策的區域，而BndB（D）是不確定性區域。

定義2［20］ 設S=（U，A∪g0gggggg）是一個決策信息系統，D∈U/Rd，令

UNC（A，D）={［x］B［x］BD，［x］B∩D≠，x∈U}，

則稱UNC（A，D）為D關于B的不確定性。

容易得到引理1。

引理1［22］ 設S=（U，A∪g0gggggg）稱為一個決策信息系統，D∈U/Rd，x∈U，則有

x∈UNC（A，D）［x］AUNC（A，D），

xUNC（A，D）［x］A∩UNC（A，D）=。

1.2 多尺度決策信息系統保持不確定性的最優尺度選擇

定義3［6］ 設S=（U，A）為多尺度信息系統，其中，U={x1，x2，…，xn}是一個非空有限集合，A={a1，a2，…，am}是一個非空條件屬性集，每個屬性aj都有s個尺度，并且對任意的1≤r≤s-1，1≤j≤m，存在一個滿射gr，r+1j：Vrj→Vr+1j，使ar+1j=gr，r+1j·arj，即對任意的x∈U，有ar+1j（x）=gr，r+1j（arj（x）），Vrj={arj（x）x∈U}是aj關于第r尺度的屬性arj的值域，gr，r+1j稱為條件屬性aj從第r尺度到第r+1的粒度轉換函數。

根據定義3，S關于第k尺度的信息系統為（U，Ak）=（U，{ak1，ak2，…，akm}），并且對任意的x∈U，有［x］A1［x］A2…［x］As，即信息粒是隨著尺度的減少而逐漸變細。

不失一般性，為方便表達，與定義3相反，文獻［20-23］規定信息粒是隨著尺度的增加而逐漸變細，以下的討論也遵循這個規定，故有

［x］As［x］As-1…［x］A1。

定義4［7］ 設S=（U，A∪g0gggggg）為多尺度決策信息系統，S=（U，A）是一個多尺度信息系統，dA是一個決策屬性，由決策屬性d誘導的等價關系為

Rd={（x，y）∈U×Ud（x）=d（y）}。

根據信息粒是隨著尺度的增加而逐漸變細，對任意的D∈U/Rd，有

RA1（D）RA2（D）…RAs（D），" RA1（D）RA2（D）…RAs（D）。

根據上下近似定義，U被分成3個互不相交的區域，即

ACP（Ak，D）=RAk（D）={［x］Ak［x］AkD，x∈U}，

REJ（Ak，D）=U-RAk（D）={［x］Ak［x］Ak∩D=，x∈U}，

UNC（Ak，D）=RAk（D）-RAk（D）={［x］Ak［x］AkD，［x］Ak∩D≠，x∈U}，

且有UNC（As，D）UNC（As-1，D）…UNC（A1，D）。

根據序貫三支決策理論，有

ACP（Ak+1，D）=ACP（Ak，D）∪K，

REJ（Ak+1，D）=REJ（Ak，D）∪J，

UNC（Ak+1，D）=UNC（Ak，D）-L。

式中：K={x∈UNC（Ak，D）［x］AkD}；J={x∈UNC（Ak，D）［x］Ak∩D=}；L={x∈UNC（Ak，D）［x］AkD∧［x］Ak∩D≠}。

多尺度決策信息系統不同尺度間的信息粒化程度不一樣，較細尺度的粒化精度較高，但認識知識需花費的精力較多，較粗尺度的粒化精度較低，而認識知識需花費的精力較少。人類的認知過程是一個由淺入深逐步推進的過程，面對具體的認識目標，人們希望以最小的精力獲取決策目標，即以最粗的尺度獲取決策目的，由于不確定性是衡量決策能力的重要指標，而決策目標有時針對具體的某個決策類，因此，提出定義5。

定義5 設S=（U，A∪g0gggggg）為MDIS，D∈U/Rd，如果存在一個1≤k≤s， 使得UNC（As，D）=UNC（Ak，D），但任意的llt;k，有UNC（As，D）UNC（Al，D）成立，則稱k是D的局部最優尺度。

根據定義5，對于D∈U/Rd，由UNC（As，D）UNC（As-1，D）…UNC（A1，D），決策類D針對最高尺度的不確定性最小，即最高尺度的決策能力最好。因此，k是保持局部決策類不確定性的最粗尺度，即保持局部決策能力不變的最優尺度。

2 增加對象條件下多尺度決策信息系統最優尺度的更新規律

對于一個多尺度決策信息系統S=（U，A∪g0gggggg），當信息系統添加一個對象y時，系統決策類的不確定性和最優尺度可能發生改變，故討論增加一個對象y是不確定性和最優尺度的更新規律。為方便表達，把增加一個對象前后對應的時刻分別記為t，t+1；

S（t）=（Ut，A∪g0gggggg），S（t+1）=（Ut+1，A∪g0gggggg）分別為時刻t，t+1對應的多尺度決策信息系統；

Ut={x1，x2，…，xn}，Ut+1={x1，x2，…，xn，y}分別為時刻t，t+1系統對應的論域；

［x］tAk，［x］t+1Ak分別為對象x第k尺度下在時刻t，t+1的等價類。

下文都是針對更新前后的系統S（t），S（t+1）開展的。因此，引理或定理的表述中不再強調更新前后的系統，也不再強調添入的對象y。

假設添入的對象y不自成一類，即存在x∈Ut，使［y］tAs=［x］tAs∪{y}。

對于Dt∈Ut/Rd，添加對象y后，Dt+1∈Ut+1/Rd是Dt的更新，則有

Dt+1=Dt∪{y}，" d（y）=d（x）， x∈Dt，Dt，" 其他。

引理2［20］ 對于任意的Dt∈Ut/Rd，Dt+1∈Ut+1/Rd是Dt的更新，1≤k≤s，則有

UNC（Ak，Dt+1）=UNC（Ak，Dt）∪［y］t+1Ak，" y∈UNC（Ak，Dt+1），UNC（Ak，Dt），" 其他。

根據引理2，顯然，有UNC（Ak，Dt）UNC（Ak，Dt+1）。

更進一步，容易得到引理3。

引理3 對Dt∈Ut/Rd，Dt+1∈Ut+1/Rd是Dt的更新，［y］t+1Ak=［x］t+1Ak∪{y}，1≤k≤s，有以下2個結論成立。

1） 如果Dt+1=Dt∪{y}，則有

UNC（Ak，Dt+1）=UNC（Ak，Dt），" ［x］tAkD，UNC（Ak，Dt）∪［x］tAk∪{y}，" ［x］tAk∩D=，UNC（Ak，Dt）∪{y}，" 其他。

2） 如果Dt+1=Dt，則有

UNC（Ak，Dt+1）=UNC（Ak，Dt）∪［x］tAk∪{y}， ［x］tAkD，

UNC（Ak，Dt），" ［x］tAk∩D=，

UNC（Ak，Dt）∪{y}，" 其他。

文獻［23］中給出最優尺度變小的充分必要條件。

定理1［23］ 設Dt∈Ut/Rd，Dt+1∈Ut+1/Rd是Dt的更新，r，R分別是Dt，Dt+1的最優尺度，［y］tAs=［x］tAs∪{y}，則Rlt;r當且僅當以下3個條件成立：

1） y∈UNC（As，Dt+1）；

2） xUNC（As，Dt）；

3） UNC（Ar-1，Dt）-UNC（As，Dt）=［x］tAs。

定理2 設Dt∈Ut/Rd，Dt+1∈Ut+1/Rd是Dt的更新，r，R分別是Dt，Dt+1的最優尺度，若［y］tAs=［x］tAs∪{y}，yUNC（As，Dt+1），則r=R。

證明：由于yUNC（As，Dt+1），根據引理1，有［y］As∩UNC（As，Dt+1）=，故［x］As∩UNC（As，Dt）=成立，又因r是決策類Dt的最優尺度，有UNC（As，Dt）=UNC（Ar，Dt），故［x］Ar∩UNC（Ar，Dt）=，分兩種情況證明yUNC（Ar，Dt+1）。

1） 當Dt+1=Dt∪［y］時，由yUNC（As，Dt+1）及［y］tAs=［x］tAs∪{y}，有

［x］tAsDt，故［x］tArDt，否則與UNC（As，Dt）=UNC（Ar，Dt）矛盾，故

［y］tAr=［x］tAr∪{y}Dt+1，即yUNC（Ar，Dt+1）。

2） 當Dt+1=Dt∪［y］時，由yUNC（As，Dt+1）及［y］tAs=［x］tAs∪{y}，有

［x］tAs∩Dt=，［x］tAr∩Dt=，否則與UNC（As，Dt）=UNC（Ar，Dt）矛盾，所以［y］tAr∩Dt+1=，即yUNC（Ar，Dt+1）。

根據引理2，UNC（As，Dt+1）=UNC（As，Dt），UNC（Ar，Dt+1）=UNC（Ar，Dt），故有UNC（As，Dt+1）=UNC（Ar，Dt+1）。

另一方面，因為r是決策類Dt的最優尺度，所以UNC（As，Dt）UNC（Ar-1，Dt），從而UNC（As，Dt+1）=UNC（As，Dt）UNC（Ar-1，Dt）UNC（Ar-1，Dt+1），所以r=R。

定理3 設Dt∈Ut/Rd，Dt+1∈Ut+1/Rd是Dt的更新，r，R分別是Dt，Dt+1的最優尺度，［y］tAs=［x］tAs∪{y}，若x∈UNC（As，Dt），則r=R。

證明：如果x∈UNC（As，Dt），那么y∈UNC（As，Dt+1），因為UNC（As，Dt）=

UNC（Ar，Dt），所以有x∈UNC（Ar，Dt），y∈UNC（Ar，Dt+1），根據引理2，可得

UNC（As，Dt+1）=UNC（As，Dt）∪{y}，且UNC（Ar，Dt+1）=UNC（Ar，Dt）∪{y}。

因此，有UNC（As，Dt+1）=UNC（Ar，Dt+1），因UNC（As，Dt）UNC（Ar+1，Dt），有

x∈UNC（Ar+1，Dt），y∈UNC（Ar+1，Dt+1），從而有UNC（A1，Dt+1）=UNC（A1，Dt）∪{y}

UNC（Ar+1，Dt）∪{y}=UNC（Ar+1，Dt+1），所以R=r。

根據定理2與定理3，添加對象y后，如果yUNC（As，Dt+1）或者x∈UNC（As，Dt），則Dt+1的最優尺度也是r，因此，只討論y∈UNC（As，Dt+1）且xUNC（As，Dt）的情況。因為r是Dt的最優尺度，故UNC（As，Dt）=UNC（Ar，Dt），從而xUNC（Ar，Dt），y∈UNC（Ar，Dt+1），根據引理1與引理3，容易得到引理4。

引理4 設r是Dt的最優尺度，y∈UNC（As，Dt+1）且xUNC（As，Dt），則有

［x］tAs∩UNC（As，Dt）=，

［x］tAr∩UNC（Ar，Dt）=，

UNC（As，Dt+1）=UNC（As，Dt）∪［x］tAs∪{y}，

UNC（Ar，Dt+1）=UNC（Ar，Dt）∪［x］tAr∪{y}。

證明：y∈UNC（As，Dt+1），xUNC（As，Dt），根據引理1可得［y］AsUNC（As，Dt+1）且［x］As∩UNC（As，Dt）=。根據引理3，可得UNC（As，Dt+1）=UNC（As，Dt）∪［x］tAs∪{y}。

由于設r是Dt的最優尺度，所以UNC（As，Dt）=UNC（Ar，Dt），從而有

［x］tAs∩UNC（As，Dt）=，

UNC（Ar，Dt+1）=UNC（Ar，Dt）∪［x］tAr∪{y}。

給出最優尺度不變與變大的充分必要條件（定理4，5）。

定理4 設Dt∈Ut/Rd，Dt+1∈Ut+1/Rd是Dt的更新，r，R分別是Dt，Dt+1的最優尺度，［y］tAs=［x］tAs∪{y}，y∈UNC（As，Dt+1），且xUNC（As，Dt），則R=r當且僅當以下兩個條件成立：

1） ［x］tAs=［x］tAr；

2） UNC（Ar-1，Dt+1）-UNC（As，Dt）［x］tAs。

證明：根據引理4，有

UNC（As，Dt+1）=UNC（Ar，Dt+1）［x］tAs=［x］tAr。

又因為UNC（As，Dt）UNC（Ar-1，Dt），所以有

UNC（As，Dt+1）UNC（Ar-1，Dt+1）UNC（As，Dt）∪［x］tAs∪{y}UNC（Ar-1，Dt+1）UNC（Ar-1，Dt+1）-UNC（As，Dt）［x］tAs。因此，有

R=rUNC（As，Dt+1）=UNC（Ar，Dt+1），

UNC（As，Dt+1）UNC（Ar-1，Dt+1）［x］tAs=［x］tAr，

UNC（Ar-1，Dt+1）-UNC（As，Dt）［x］tAs。

定理5 設Dt∈Ut/Rd，Dt+1∈Ut+1/Rd是Dt的更新，r，R分別是Dt，Dt+1的最優尺度，［y］tAs=［x］tAs∪{y}，y∈UNC（As，Dt+1），xUNC（As，Dt），則Rgt;r當且僅當

［x］tAs［x］tAr。

證明：根據引理4，有

Rgt;rUNC（As，Dt+1）UNC（Ar，Dt+1）UNC（As，Dt）∪［x］tAs∪{y}UNC（Ar，Dt）∪［x］tAr∪{y}［x］tAs［x］tAr。

例1

動態多尺度決策信息系統（例1），如表1所示。更新動態MDSI決策類的局部最優尺度。

設Ut={x1，x2，…，x8}，當對象y，z被添加到系統后，對最優尺度的更新進行研究。經計算可得

Ut/Rd={Dt，Et}={{x1，x2，x3，x4}，{x5，x6，x7，x8}}，

Ut/RA3={{x1}，{x2}，{x3}，{x4，x5}，{x6}，{x7}，{x8}}，

Ut/RA2={{x1}，{x2，x3}，{x4，x5}，{x6}，{x7，x8}}，

Ut/RA1={{x1}，{x2，x3，x4，x5}，{x6，x7，x8}}，

UNC（A3，Dt）=UNC（A3，Et）={x4，x5}，

UNC（A2，Dt）=UNC（A2，Et）={x4，x5}，

UNC（A1，Dt）=UNC（A1，Et）={x2，x3，x4，x5}。

因此，Dt，Et的局部最優尺度都是2。

當添入對象y時，有Et+1=Et∪{y}，經計算可得，［y］t+1A3=［x8］tA3∪{y}，

UNC（A3，Dt+1）={x4，x5，x8，y}，UNC（A3，Et+1）={x4，x5，x8，y}，故

［y］t+1A3=［x8］tA3∪{y}，y∈UNC（A3，Dt+1），x8UNC（A3，Dt），［x8］tA3［x8］tA2，

根據定理5，Dt+1的最優尺度大于Dt的最優尺度，

由［y］t+1A3=［x8］tA3∪{y}，y∈UNC（A3，Et+1），x8UNC（A3，Et），［x8］tA3［x8］tA2，Et+1的最優尺度大于Et的最優尺度。經計算Dt+1，Et+1的最優尺度都為3。

當添入對象z時，有Dt+1=Dt∪{z}，經過計算可得到［z］t+1A3=［x1］tA3∪{z}，

UNC（A3，Dt+1）=UNC（A3，Et+1）={x4，x5}，zUNC（A3，Dt+1），zUNC（A3，Et+1），

由定理2，Dt+1與Et+1的最優尺度都不變，都為2。

由于［x2］tA3=x2，［x3］tA3=x3，所以

UNC（A1，Dt+1）-UNC（A3，Dt）UNC（A1，Dt）-UNC（A3，Dt）={x2，x3}≠［x2］tA3，

UNC（A1，Et+1）-UNC（A3，Et）UNC（A1，Et）-UNC（A3，Et）={x2，x3}≠［x3］tA3。

根據定理1，無論加入何對象，最優尺度都不會變小。

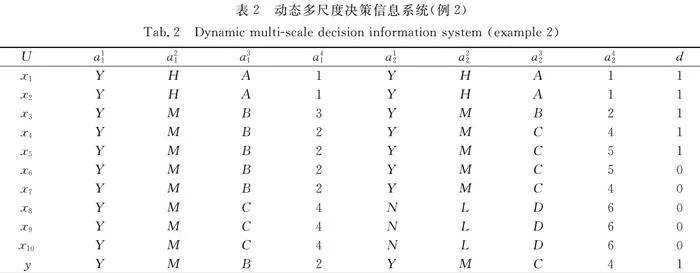
例2 動態多尺度決策信息系統（例2），如表2所示。更新動態MDSI決策類的局部最優尺度。

經計算可得

Ut/Rd={Dt，Et}={{x1，x2，x3，x4，x5}，{x6，x7，x8，x9，x10}}，

Ut/RA4={{x1，x2}，{x3}，{x4，x7}，{x5，x6}，{x8，x9，x10}}，

Ut/RA3={{x1，x2}，{x3}，{x4，x5，x6，x7}，{x8，x9，x10}}，

Ut/RA2={{x1，x2}，{x3，x4，x5，x6，x7}，{x8，x9，x10}}，

Ut/RA1={{x1，x2，x3，x4，x5，x6，x7}，{x8，x9，x10}}，

UNC（A4，Dt）=UNC（A4，Et）={x4，x5，x6，x7}，

UNC（A3，Dt）=UNC（A3，Et）={x4，x5，x6，x7}，

UNC（A2，Dt）=UNC（A2，Et）={x3，x4，x5，x6，x7}，

UNC（A1，Dt）=UNC（A1，Et）={x1，x2，x3，x4，x5，x6，x7}。

因此，Dt，Et的最優尺度都是3，

添入對象y時，由表2可得，Dt+1=Dt∪{y}，Et+1=Et，且［y］t+1A4=［x4］tA4∪{y}，

由x4∈UNC（A4，Dt），x4∈UNC（A4，Et），根據定理3，Dt+1與Et+1的最優尺度都不變，仍為2。

3 結束語

尋找最優尺度是多尺度決策信息系統的一個核心問題，決策類的不確定性是系統決策能力的一個重要的衡量標準。在最細尺度下，系統的決策能力最優。以局部決策類在最細尺度下的不確定性作為度量指標，采用增量學習方法，在對象動態增加的環境下，研究多尺度的決策信息系統保持局部決策類不確定性的最優尺度的更新規律，給出在添加一個對象條件下，最優尺度不變和變大的充分必要條件。文中給出了添加對象后系統最優尺度更新的一種判別方法，進一步完善了這一課題的研究，具有一定的理論價值和實踐價值。

今后，將進一步研究對象動態增加環境下多尺度覆蓋決策信息系統和集值決策信息系統的最優尺度更新規律，并探索將所得的結果推廣到模糊集的情形。

參考文獻：

［1］ 王國胤，張清華，胡軍.粒計算研究綜述［J］.智能系統學報，2007，2（6）：8-26.DOI：10.3969/j.issn.1673-4785.2007.06.002.

［2］ LI Jinhai，HUANG Chenchen，QI Jianjun，et al.Three way cognitive concept learning via multi-granularity［J］.Information Sciences，2017，378：244-263.DOI：10.1016/j.ins.2016.04.051.

［3］ HUANG Zhenhuang，LI Jinjin，QUAN Yuhua.Noise-tolerant fuzzy β covering based multigranulation rough sets and feature subset selection［J］.IEEE Transactions Fuzzy Systems，2022，30（7）：2721-2735.DOI：10.1109/TFUZZ.2021.3093202.

［4］ YAO Yiyu.Three-way decisions with probabilistic rough sets［J］.Information Sciences，2010，180：341-353.DOI：10.1016/j.ins.2009.09.021.

［5］ 王志煥，游小英，李偉康，等.模糊廣義決策信息系統的證據特征與信任約簡［J］.華僑大學學報（自然科學版），2020，41（5）：683-689.DOI：10.11830/ISSN.1000-5013.202003026.

［6］ WU Weizhi，LEUNG Yi.Theory and applications of granular labelled partitions in multi-scale decision tables［J］.Information Sciences，2011，181：3878-3897.DOI：10.1016/j.ins.2011.04.047.

［7］ WU Weizhi，LEUNG Yi.A comparison study of optimal scale combination selection in generalized multi-scale decision tables［J］.International Journal of Machine Learning and Cybernetics，2020，11：961-972.DOI：101007/s13042-019-00954-1.

［8］ SHE Yanhong，QIAN Zhuohao，HE Xiaoli，et al.On generalization reducts in multi-scale decision tables［J］.Information Sciences，2021，555：104-124.DOI：10.1016/j.ins.2020.12.045.

［9］ LI Feng，HU Baoqing.Stepwise optimal scale selection for multi-scale decision tables via attribute significance［J］.Knowledge-Based Systems，2017，129：4-16.DOI：10.1016/j.knosys.2017.04.005.

［10］ HUANG Zhenhuang，LI Jinjin，DAI Weizhong，et al.Generalized multi-scale decision tables with multi-scale decision attributes［J］.International Journal of Approximate Reasoning，2019，115：194-208.DOI：10.1016 /j.ijar.2019.09.010.

［11］ 陳應生，李進金，林榮德，等.多尺度集值決策信息系統［J］.控制與決策，2002，37（2）：455-462.DOI：10.13195/j.kzyjc.2020.0882.

［12］ 顧沈明，陸瑾璐，吳偉志.廣義多尺度決策系統的局部最優粒度選擇［J］.山東大學學報（理學版），2018，53（8）：1-8.DOI：10.6040/j.issn.1671-9352.4.2018.184.

［13］ 馬周明，黃閩，林國平，等.基于超圖的多尺度決策信息系統最優尺度選擇［J］.閩南師范大學學報（自然科學版），2023，36（4）：1-15.DOI：10.16007/j.cnki.issn2095-7122.2023.04.001.

［14］ 吳偉志，孫鈺，王霞，等.不協調廣義多尺度決策系統的局部最優尺度組合選擇［J］.模式識別與人工智能，2021，34（8）：689-700.DOI：10.16451/j.cnki.issn1003-6059.202108002.

［15］ YANG Xin，LI Tianrui，LIU Dun.A unified framework of dynamic three-way probabilistic rough sets［J］.Information Sciences，2017，420：126-147.DOI：10.1016/j.ins.2017.08.053.

［16］ ZHANG Qinghua，LV Gongxun，CHEN Yuhong，et al.A dynamic three-way decision model based on the updating of attribute values［J］.Knowledge-Based Systems，2018，142：71-84.DOI：10.1016/j.knosys.2017.11.026.

［17］ HE Shifan，WANG Yangming，PAN Xiaohong，et al.A novel behavioral three-way decision model with application to the treatment of mild symptoms of COVID-19［J］.Applied Soft Computing，2022，124：109055.DOI：10.1016/j.asoc.2022.109055.

［18］ DENG Jiang，ZHAN Jianming，WU Weizhi.A three-way decision methodology to multi-attribute decision-making in multi-scale decision information systems［J］.Information Sciences，2021，568：175-198.DOI：10.1016/j.ins.2021.03.058.

［19］ LUO Chuan，LI Tianrui，HUANG Yanhong，et al.Updating three-way decisions in incomplete multi-scale information systems［J］.Information Sciences，2019，476：274-289.DOI：10.1016/j.ins.2018.10.012.

［20］ HAO Chen，LI Jinhai，FAN Min，et al.Optimal scale selection in dynamic multi-scale decision tables based on sequential three-way decisions［J］.Information Sciences，2017，415/416：213-232.DOI：10.1016/j.ins.2017.06.032.

［21］ CHEN Yingsheng，LI Jinhai，LI Jinjin，et al.A further study on optimal scale selection in dynamic multi-scale decision information systems based on sequential three-way decisions［J］.International Journal of Machine Learning amp; Cybernetics，2022，13：1505-1515.DOI：10.1007/s13042-021-01474-7.

［22］ LI Jinhai，FENG Ye.Update of optimal scale in dynamic multi-scale decision information systems［J］.International Journal of Approximate Reasoning，2023，152：310-324.DOI：10.1016/j.ijar.2022.10.020.

［23］ CHEN Yingsheng，LI Jinhai，LI Jinjin，et al.Sequential 3WD-based local optimal scale selection in dynamic multi-scale decision information systems［J］.International Journal of Approximate Reasoning，2023，152：221-235.DOI：10.1016/j.ijar.2022.10.017.

（責任編輯： "錢筠" 英文審校： 黃心中）

通信作者： 李進金（1960-），男，教授，博士，博士生導師，主要從事一般拓撲學與不確定性分析的研究。E-mail：jinjinlimnu@126.com。

基金項目： 國家自然科學基金資助項目（12271191， 11871259）； 福建省自然科學基金資助項目（2022J01306）https：//hdxb.hqu.edu.cn/