狹義相對論中量子泊松括號的變換及其物理意義

摘要：將泊松括號從分析力學過渡到量子力學，其物理意義是很深刻的；進一步變換到狹義相對論四維時空中，其四維的量子力學泊松括號所具有的對稱性和洛倫茲不變性是非常有趣的，由此給出時空光錐上四維量子力學矢量的非對易泊松括號，推導出新的物理創意和結果，探索物理量之間新的量子非對易關系。以此將量子力學與狹義相對論力學結合起來，思考近代物理中的對稱性與守恒量問題，并通過非對易關系溝通物質與時空的物理圖像及其聯系，這些創新性工作在物理層面上具有重要的意義。

關鍵詞：狹義相對論；量子泊松括號；四維量子力學矢量；量子非對易關系

中圖分類號：O412文獻標志碼：A泊松括號最先是在哈密頓分析力學中出現，狄拉克將其與量子力學聯系起來，引入量子力學泊松括號，并解釋其量子力學中深刻的物理意義[1-6]。將量子力學泊松括號變換到狹義相對論四維時空中是非常有趣的，我們注意到四維時空中物理量的對稱性和洛倫茲不變性，愛因斯坦從四維動量的對稱性和洛倫茲不變性推出了質量與能量的關系，給出了著名的質能方程[7]，其劃時代的成果指導了人類對于核能的研發和應用。沿此思路，將量子力學泊松括號引入狹義相對論的四維形式，并探索其對稱性和洛倫茲不變性，發現一些有趣的性質和有用的結果，特別是可以從狹義相對論量子力學泊松括號的對稱性和洛倫茲不變性探索與尋找新的量子非對易關系。

1 經典泊松括號

2 量子力學泊松括號

3 狹義相對論量子力學泊松括號

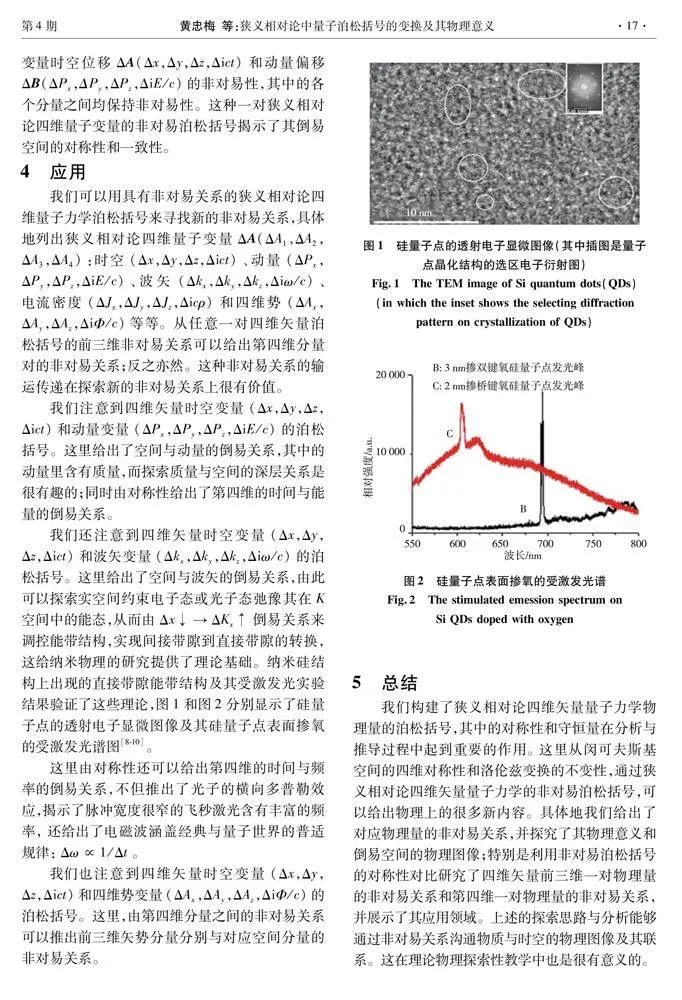
4 應用

5 總結

我們構建了狹義相對論四維矢量量子力學物理量的泊松括號，其中的對稱性和守恒量在分析與推導過程中起到重要的作用。 這里從閔可夫斯基空間的四維對稱性和洛倫茲變換的不變性，通過狹義相對論四維矢量量子力學的非對易泊松括號，可以給出物理上的很多新內容。具體地我們給出了對應物理量的非對易關系，并探究了其物理意義和倒易空間的物理圖像；特別是利用非對易泊松括號的對稱性對比研究了四維矢量前三維一對物理量的非對易關系和第四維一對物理量的非對易關系，并展示了其應用領域。上述的探索思路與分析能夠通過非對易關系溝通物質與時空的物理圖像及其聯系。這在理論物理探索性教學中也是很有意義的。參考文獻：

[1]DIRAC P A M. 狄拉克量子力學原理［M］. 凌東波， 譯. 北京： 機械工業出版社， 2018： 86-99.

［2］ П. Д. 朗道， Е. М. 栗弗席茲. 力學［M］. 李俊峰， 譯. 5版. 北京： 高等教育出版社， 2007： 137-140.

［3］ 曾謹言，喀興林. 對應原理在量子論發展中所起的作用［J］. 大學物理，1985， 1（9）： 10-14.

［4］ 林靜， 胡化凱. 對應原理在矩陣力學建立過程中的作用［J］. 安徽大學學報（自然科學版）， 1996， 20（4）： 99-105.

［5］ 黃永義，量子力學的基本對易關系［J］. 物理與工程， 2021， 31（1）： 8-15.

［6］ 郭艷輝. 對易關系在量子力學中的重要討論［J］. 高等函授學報（自然科學版）， 2011， 24（1）： 31-33.

［7］ 劉遼， 費保俊， 張允中. 狹義相對論［M］. 北京： 科學出版社， 2018： 123， 141.

［8］ HUANG W Q， HUANG Z M， MIAO X J， et al. An all-silicon laser by coupling between electronic localized states and defect states of photonic crystal［J］. Applied Surface Science， 2012， 258： 3033-3038.

［9］ HUANG W Q， HUANG Z M， CHENG H Q，et al. Electronic states and curved surface effect of silicon quantum dots［J］. Applied Physics Letters， 2012， 101： 171601.

［10］HUANG W Q， LIU S R， HUANG Z M， et al. Lasing with pumping levels of si nanocrystals on silicon wafer［J］. Nanoscale Research Letters， 2016， 11： 500.

（責任編輯：曾晶）

Poisson Brackets in Four-Dimensional Vector of Special Relativity

HUANG Zhongmei HUANG Weiqi

（1.Institute of Nanophotonic Physics， College of Materials and Metallurgy， Guizhou University， Guiyang 550025， China；

2.State Key Laboratory of Surface Physics， Key Laboratory of Micro and Nano Photonic Structures

（Ministry of Education）， Department of Physics， Fudan University， Shanghai 200433， China）Abstract： In the special relativity， there is the inherent symmetry of the four-dimensional continuous domain of time and space， which is called Minkowski space. It is of great significance for classical mechanics and quantum mechanics to study the Poisson brackets of four-dimensional vector of special relativity. Classical Poisson bracket is an important operation in Hamiltonian mechanics， which is mainly used in classical mechanics and mathematics. It is more interesting that the symmetry and the Lorentz invariance of the Poisson brackets in four-dimensional vectors occur in the special relativity. We use the correspondence principle to transfer the classical Poisson bracket into the quantum form of Poisson bracket， which leads to the Heisenberg uncertainty relation. The four-dimensional Poisson brackets of special relativity in quantum mechanics will lead to some wonderful physical phenomena， in which some new uncertainty principle will be explored.

Key words： special relativity; Poisson bracket; four-dimensional vector; uncertainty principle