基于GA-BP神經網絡的列車輪對振動信號研究
云善起,薛鑫,牟茂源,劉媛媛
(青島杰瑞工控技術有限公司,山東 青島 266520)
0 引言
隨著我國鐵路運輸行業的迅速發展,列車運行經歷了多次提速,運行中的安全性愈發受到重視[1]。輪對作為與軌道直接接觸的走行部件,其工作環境惡劣,在列車高速行駛過程中極易受到沖擊造成損傷[2],從而影響列車運行的安全性。
列車在高速運行過程中,輪對不僅會因為正常行駛產生振動,還會由于道岔、鋼軌不平等影響而受到沖擊,輪對的踏面損傷現象比較普遍。因此,對輪對故障監測和診斷關鍵性技術進行研究,及時準確地對輪對故障做出預報,對列車的安全運行意義重大[3]。
本文針對輪對振動信號復雜、故障難以準確診斷的問題,對輪對故障信號進行特征分析,以此為基礎,建立相應的故障診斷模型,以滿足列車運行過程中及時、準確地診斷輪對故障的要求。
1 小波包分解原理
輪對與鋼軌發生沖擊時產生的振動為非穩態振動,將振動信號進行小波包分解可以對其頻域特征與時域特征進行同步分析[3],從而提取出相應的輪對故障特征。
小波分析具有多分辨率分析的特點,且在時頻兩域都能夠表征信號局部特征[4]。但此種方法只能對信號低頻進行再分解,對高頻部分不做任何處理。小波包分解在小波分析的基礎上,能夠對信號進行更加精細的分析,第一次分解后得到信號的高頻部分和低頻部分[5],再次分解時可以將兩個部分同時進行再分解。
令輪對振動信號為S,可將信號進行分解得S=T(1,0)?T(1,1)=T(2,0)?T(2,1)?T(2,2)?T(2,3)=…=T(I,J),其中,I=1,2,3,…,J=2I-1。
2 輪對振動信號處理
2.1 故障信號的小波包分解
使用一個正常輪對與一個踏面故障輪對進行模擬實驗,選擇1 000個采樣點進行振動信號的采集。兩組輪對振動信號如圖1所示,對比可觀察到踏面故障輪對的振動幅度更大。
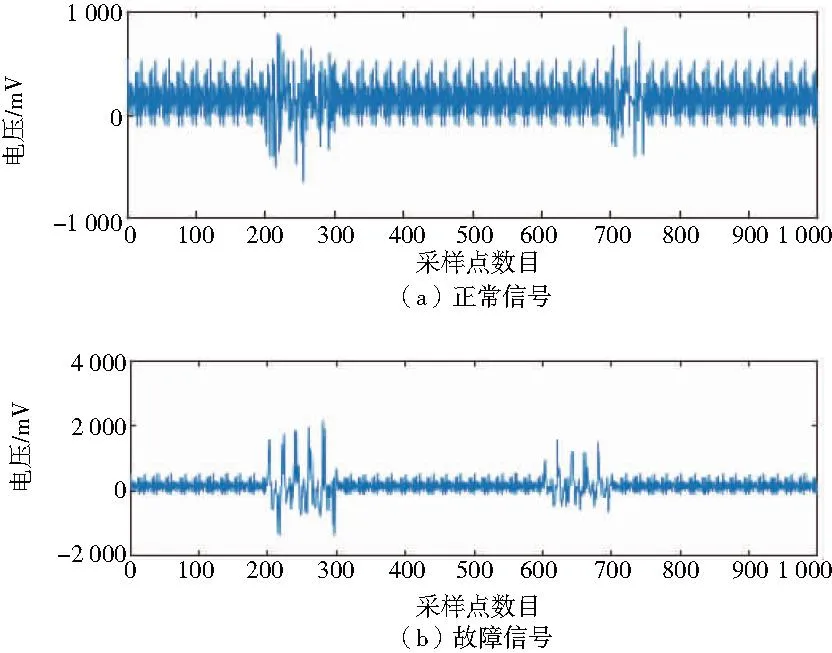
圖1 正常輪對信號與故障輪對信號
將2組信號分別使用小波包算法進行3層分解,得到不同頻域信號特征如圖2、圖3所示。
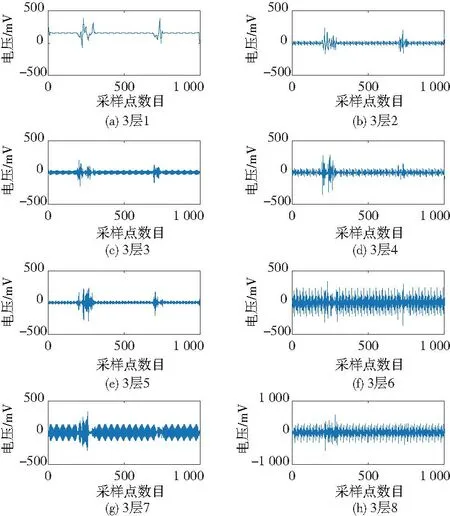
圖2 正常輪對信號分解結果
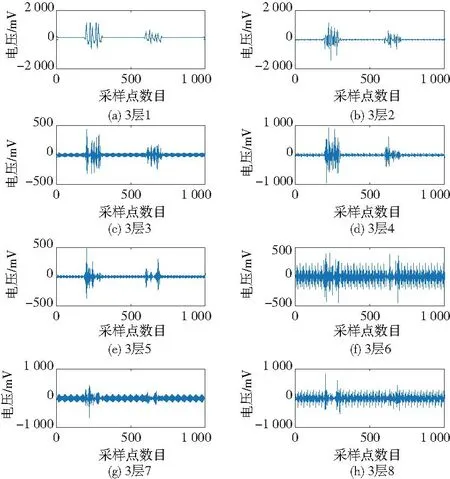
圖3 故障輪對信號分解結果
2.2 故障信號特征提取
輪對振動信號經過小波包3層分解之后,將不同分解尺度上的信號能量計算出來,即得到了分解后的信號空間能量特征[6]。具體過程如下:
1)將各節點的小波包系數進行重構,重構系數為Mjk;
2)計算分解后各子信號的能量:
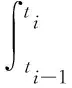
(1)
3)計算信號總能量:
(2)
4)計算子信號能量在整個信號總能量中所占的比重:
(3)
根據上述步驟將故障信號進行3層小波包分解后,計算出各子信號能量所占信號總能量比值,并繪制柱狀圖如圖4所示。
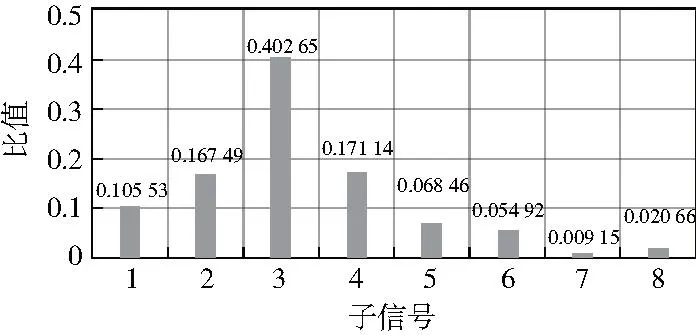
圖4 分解故障信號能量分布柱狀圖
分析圖4可知整個信號的能量主要分布在1—5層,所占比重達到91.5%左右,6—8層占比不足10%,所以可將1—5層作為故障信號的特征向量,可表示為
P=[Q31,Q32,Q33,Q34,Q35]
(4)
經過小波包分解得到的故障信號特征向量可以為下一步的輪對故障診斷提供理論依據。
3 輪對故障診斷算法
3.1 GA-BP算法原理
BP神經網絡是解決非線性問題的一種常見方法,其本質是求解函數的最優解問題,根據誤差改變下次迭代的權值和閾值,使得實際輸出不斷趨近期望輸出。但這種方法存在收斂性慢、易陷入局部極值的缺點[7],難以實現輪對故障的精確診斷。
遺傳算法模擬生物遺傳的方式,通過對編碼群體進行一定的遺傳操作,評估適應度保留最優個體,具有較好的收斂性和較高的魯棒性。因此,考慮采用遺傳算法對BP神經網絡的權值和閾值進行優化,避免陷入局部最優。同時,優化過程不會影響神經網絡的拓撲結構[8]。改進的GA-BP神經網絡算法流程如圖5所示。
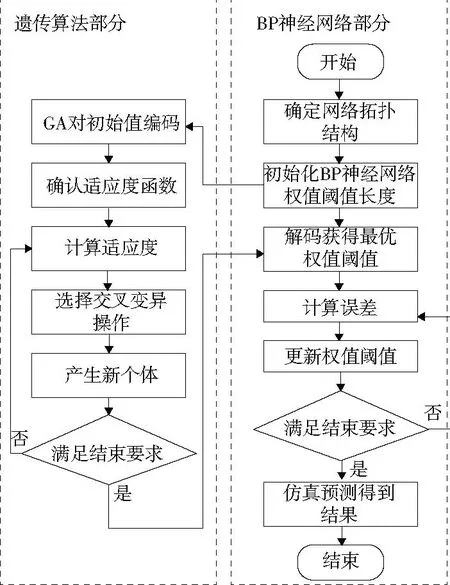
圖5 GA-BP神經網絡算法流程圖
初始化BP神經網絡的權值閾值長度作為遺傳算法的輸入,通過遺傳算法適應度函數計算個體適應度,循環執行交叉變異操作直到獲得最優權值閾值[9],進行神經網絡訓練,從而建立輪對故障神經網絡診斷模型。
3.2 基于GA-BP的輪對故障診斷模型
將故障信號的特征向量P作為輸入構建神經網絡,其拓撲結構為5-3-1,即輸入層神經元數目為5,隱含層神經元數目為3,輸出層神經元數目為1。
遺傳算法的基本步驟如下[10]。
1)個體編碼
本文利用遺傳算法求BP神經網絡最優權值閾值,采用實數編碼,其編碼方式為
L=n×h+h×m+h+m
(5)
式中:L為編碼長度;n為輸入層神經元數目;h為隱含層神經元數目;m為輸出層神經元數目。易知編碼長度為22。
2)初始群體的產生
遺傳算法通過對初始群體數據的進化獲得最優解。一般來說群體規模越大,最優解越容易獲得。遺傳迭代次數表示算法滿足結束標志的參數。本文將群體規模設為50,迭代次數為100。
3)適應度計算
遺傳算法中通過個體適應度值評定其優劣程度,決定個體遺傳概率,以此得到最優解。適應度決定了群體的進化方向。本文選擇適應度函數為
(6)
式中:m為BP神經網絡輸出層節點數量;dk、yk分別為輸出層第k個節點的期望輸出和實際輸出。
4)選擇運算
選擇運算通過某種規律篩選出進化群體中適應度較高的個體將其遺傳至下一代群體中。選擇公式為
(7)
式中fi表示個體i的適應度。
5)交叉運算
交叉運算選擇適當的交叉概率以相互交換某兩個體之間的部分染色體,以產生新個體。算法收斂速度隨交叉概率提高而提高。本文選擇交叉概率為0.6。
6)變異運算
變異運算是指對個體的某個或某些基因座上的基因值按照一較小的概率進行改變,從而產生新個體。本文選擇變異概率為0.1。
4 輪對故障診斷實驗
4.1 仿真實驗結果
將輪對故障診斷模型的各個參數確定后,即可以信號特征向量作為輸入,對診斷模型進行訓練。實驗采集300組正常振動信號、300組踏面擦傷振動信號以及300組踏面剝離振動信號,對其進行小波包分解后得到特征向量。選取部分特征向量如表1所示。
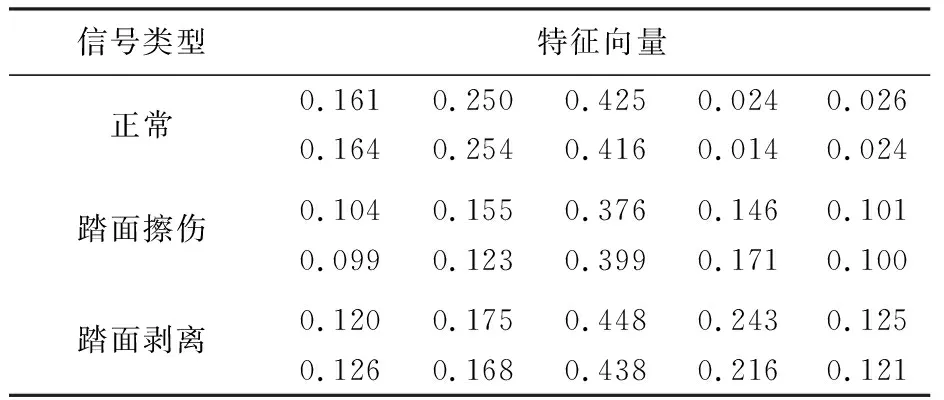
表1 3組信號部分特征向量
3種信號分別取200組作為訓練樣本輸入故障診斷模型,正常信號編碼為0,踏面擦傷信號編碼為1,踏面剝離信號編碼為2,設置改進后的BP神經網絡學習速率為0.01,迭代次數為5 000,期望誤差為0.000 01。遺傳算法適應度曲線如圖6所示。
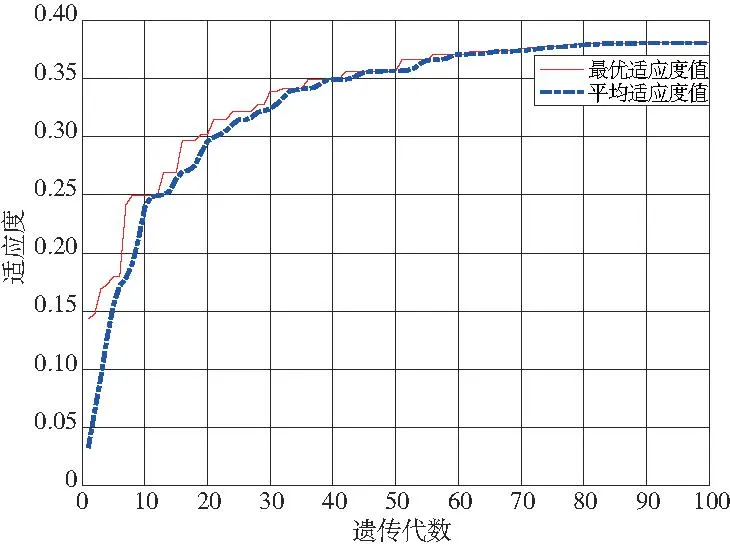
圖6 遺傳算法適應度曲線
由圖6可以看出,在開始的位置種群的平均適應度很低,遺傳代數達到80代左右,最優適應度與平均適應度趨于穩定且較高的位置,約為0.38。
GA-BP故障診斷模型訓練好之后,為了驗證其診斷效果,選取20組正常振動信號、15組踏面擦傷振動信號以及15組踏面剝離振動信號,分別采用未優化的BP神經網絡模型與優化后的GA-BP神經網絡模型進行診斷實驗,結果如圖7、圖8所示。
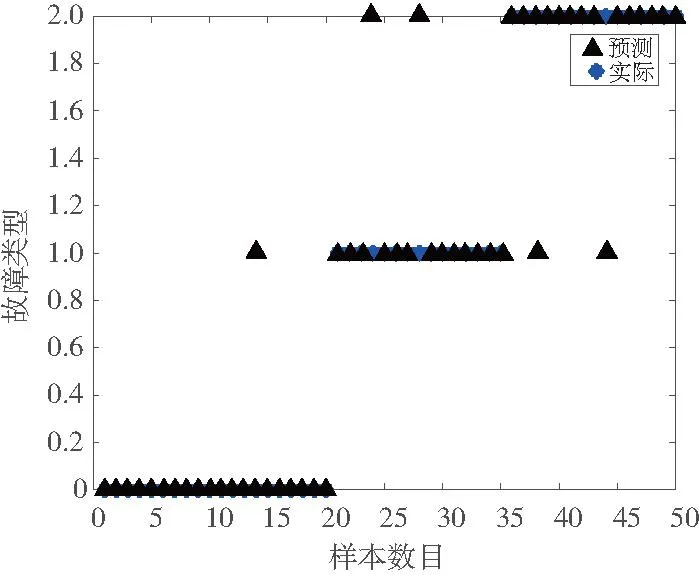
圖7 BP神經網絡模型診斷結果
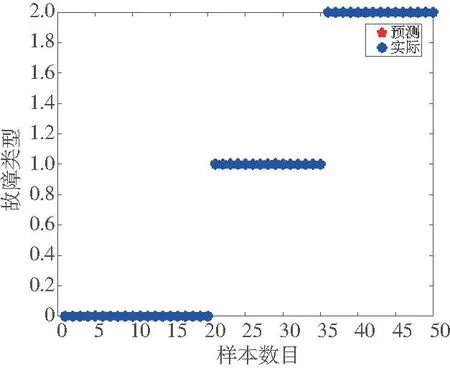
圖8 GA-BP神經網絡模型診斷結果
由圖7和圖8對比可以看出,采用未優化的BP神經網絡進行故障診斷準確率為90%,采用GA-BP神經網絡模型進行故障診斷準確率達到了100%。試驗結果表明:經遺傳算法優化的BP神經網絡故障診斷模型準確率更高,診斷結果更加準確,為振動監控系統提供了診斷算法理論基礎,可以更好地應用于列車輪對故障診斷之中。
4.2 輪對故障監控系統軟件設計
針對輪對故障診斷系統的需要,設計了上位機監控軟件。軟件的主要開發環境為Visual Studio 2019,在.Net平臺下采用C#語言編程來實現,核心診斷算法采用MATLAB編程封裝成庫函數,嵌入到系統中,二者混合編程實現系統全部功能的開發。軟件的主要功能包括輪對信息的采集、數據的傳輸、數據的存儲和分析、故障的診斷、結果的實時展示等。軟件主界面如圖9所示。
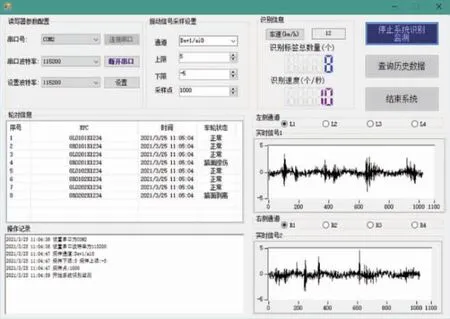
圖9 監控軟件工作界面
進入系統后將讀寫器參數以及振動信號采樣參數設置完成,點擊“開始系統識別”按鈕,系統自動開始識別經過監測區域的列車輪對信息和振動信號,頁面開始實時顯示左、右兩側車輪傳感器振動信號,并存入到系統數據庫中,通過調用診斷算法判斷輪對狀態,并將結果顯示到頁面上的輪對信息中。
通過實驗對識別系統軟件的各項功能進行測試,結果表明上位機軟件可以實現輪對振動信號的實時監控與輪對故障的準確判斷,能夠實現輪對信息的有效管理與追溯。
5 結語
本文針對列車輪對故障診斷問題,采用小波包算法對輪對振動信號進行分解與重構,得到輪對振動信號特征向量,以此作為輸入建立GA-BP神經網絡診斷模型,采集不同故障下的輪對振動信號,對診斷模型進行訓練和測試,驗證了GA-BP神經網絡診斷模型故障識別準確率更高,并設計了上位機監控軟件,實現輪對信息監測的實時化與可視化,對于實現列車輪對狀態的動態監測具有重要意義。

