考慮凈負荷不確定性的梯級水電站日前調峰模型構建

石魏敏

(廣州市水務科學研究院有限公司，廣東 廣州 510220)

1 基于凈負荷不確定性的梯級水電站日前調峰模型研究

1.1 考慮凈負荷不確定性的調峰模型研究

近些年，我國社會用電量持續增長且峰谷差不斷增大，伴隨著新能源的高速發展，其在一定程度上降低了傳統化石能源的消耗并減少了環境污染，然而風、光等新能源功率的波動和間歇影響使得電網凈負荷的精準預測出現困難，這種情況較難保證電網運行的安全性和經濟性[1]。新能源電力會因為干旱、雨雪等異常天氣影響電力系統對用電負荷的準確預測，除此之外，清潔能源具備的波動性、間歇性和不確定性等顯著特征也會對用電負荷的準確預測產生影響。因此而存在的負荷預測誤差會打亂電網計劃的電力平衡，進而增加了電網的控制負擔[2]。與此同時，調峰電源會面臨著預測峰谷和實際峰谷之間出現差異的風險，此時進行調峰有可能反而會拉大系統負荷峰谷差。因此，關于凈負荷的不確定性和合理安排電力資源成為研究重點，凈負荷數據的表現形式是與歷史時刻相關的時序序列，可用滯后相關性來體現凈負荷的數據關聯性，如式(1)：

(1)

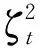
圖1 DDPMM概率模型

凈負荷的隨機參數包含在總功率平衡約束和支路潮流約束中，可被歸結為節點上的凈負荷不確定量。常規發電機都具備一定的調節能力，使其能夠在合理分擔系統功率不平衡量的同時也能應對負荷的預測誤差和波動，在一定程度上實現功率平衡和新能源功率的完全接納。發電系統的所有在線發電機在應對凈負荷波動時的調節能力以仿射形式與凈負荷的波動程度相匹配[3]。對于支路潮流約束中的隨機參數可以通過魯棒線性化方法來消除。凈負荷的擾動會對電力系統的運行成本造成影響，因為，其中會涉及因凈負荷而調用設備的情況，此舉會影響電力系統的啟停成本、運行成本、備用成本、期望停電損失等，然而，并非所有凈負荷擾動都需要調用設備，在其波動較小的情況下產生的影響較小，不需要做太多調整，隨著波動的增加系統的各類運行成本也在增加，此時則需要酌情調整總備用。圖2表示不同凈負荷波動范圍的總備用調整變化趨勢，從圖中可以清楚地反映出凈負荷的波動對調整備用的影響。

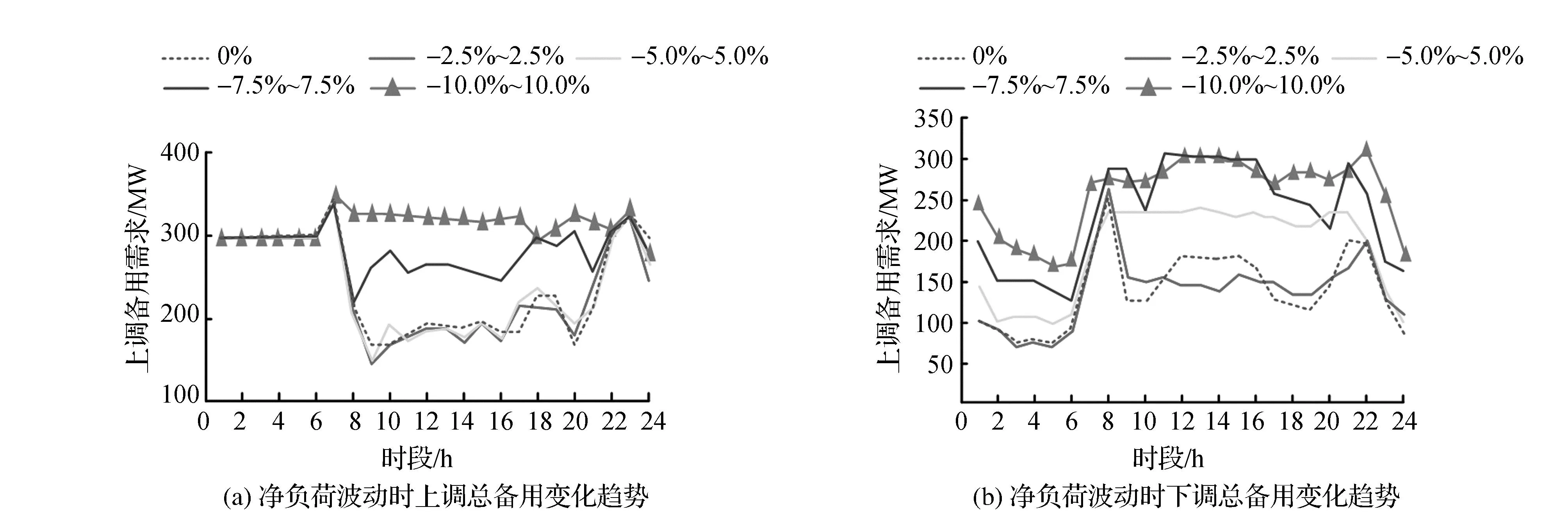
圖2 不同凈負荷波動范圍的總備用調整變化趨勢

電能具有不能大量儲存的特點，因此，發電部門會根據用電的需求發出電量，電負荷會因為用電需求而發生變化，在此過程中，發電部門為維持功率平衡而改變發電機的出力以適應用電負荷的變化。調峰則是一種在用電高峰時期為解決電網超負荷的情況而投入正常運行以外的發電機組，以此來滿足正常需求的改變電負荷的手段。調峰也是我國電力系統一直面臨的重要調度難題，作為我國能源巨頭的火電裝機因調峰不靈活且調峰費用高而面臨的調峰壓力較為嚴峻；風光等能源則有著較大的波動性和預測困難性，這些客觀因素使其調峰過程面臨著較大的挑戰。考慮凈負荷不確定性的調峰模型可以更準確地對系統電負荷進行預測，進而便于電力系統進行電力調度。

1.2 結合凈負荷不確定性的梯級水電站日前調峰模型

與火電、風光等能源相比，水電具備清潔低耗、啟用靈活等特點，是一種優質的調峰電源，能夠在一定程度上保證電力的穩定運行。我國水電調峰凈負荷的不確定性主要來自光伏出力預測不確定性、風電出力預測不確定性和負荷預測的不確定性。因此，在水電參與調峰時也應當考慮到風電出力時的不確定性和反調峰性，避免出現進一步拉大負荷峰谷而增加調峰壓力的情況。圖3表示水電調峰偏差示意圖，如圖3(a)所示，若按照預測凈負荷，其余荷在33 h時段已經趨于平穩，但實際的凈負荷卻與此存在偏差，如圖3(b)所示，此時若按照預測凈負荷進行調峰則會出現兩個新峰，表明此舉未達到調峰目的，反而會威脅到電網的安全運行。

圖3 調峰偏差示意圖

由上述可知，本文旨在充分考慮水電調峰凈負荷的不確定性，及時應對梯級水電站復雜的水利關系，以此制定更合理的調峰計劃來滿足電網電力平衡的需求。本次模型的構建選擇場景分析法來描述凈負荷的不確定性，利用多場景期望值優化來量化不確定風險，同時以余荷平均距平絕對值最小為調峰目標，如式(2)：

(2)

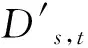
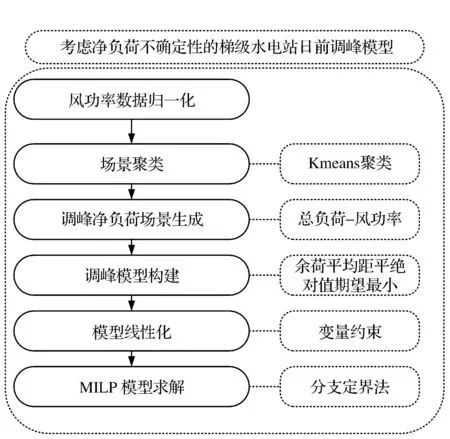
圖4 考慮凈負荷不確定性的梯級水電站日前調峰模型流程

2 考慮凈負荷不確定性的調峰模型試驗結果分析

試驗首先將一整天劃分為24個時段，選取某地區某月兩日不同預測和實際風電出力過程，分別記為A、B組，A、B組的場景同屬于枯期，出力變幅和梯級日總電量均保持一致，A組的日出水位略高于B組。兩組風電出力的過程如圖5所示，從圖中不難發現兩組的預測與實際都存在一定的誤差，其中，A組實際與預測風功率形狀在峰谷時段存在巨大差異，后針對兩組風功率采用多場景期望模型對調峰結果進行分析。多場景相比單場景的計算需要添加額外變量及約束，隨著聚類場景的增加，其模型的求解難度也會增加。

圖5 A、B兩組風功率預測和實際過程

針對風功率引起的凈負荷不確定性展開研究，利用Kmeans算法聚類某月風電出力的4類場景，該4種場景在大小和形狀上存在著明顯差異，能夠充分描述該地區該月關于風電出力的不確定性，其出現的概率分別為14%、33%、30%、27%。表1表示在不同的風電滲透率下多場景的凈負荷峰谷差，從表中數據可以看出，在接入風電出力后，場景a、b、c增大了凈負荷峰谷差，并且凈負荷峰谷差隨著滲透率的增加而增大，呈現出反調峰出力過程的特點；場景d減小了凈負荷峰谷差，不過隨著滲透率的增加，峰谷差先減小后增大。實際場景和預測場景兩者均減小了凈負荷峰谷差，但同樣的隨著滲透率的增加，凈負荷峰谷差先減小后增大。

表1 不同風電滲透率多場景下的凈負荷峰谷差

選擇15%的風電滲透率作為研究背景，對上述A、B兩組采用多場景分析法進行計算并分析凈負荷不確定性對調峰的影響。表2表示A、B兩組在實際、預測和多場景期望下的調峰指標統計值。從表中數據可以看出，處于三種場景下的水電對實際凈負荷調節之后的余荷峰谷差的減小率無顯著差別，但是，對于多場景期望目標函數，兩組均優于預測單場景，由此可以表明，多場景期望模型下的水電調峰過程與實際場景下的出力過程更為相似，同時也驗證了提出的模型對考慮凈負荷不確定性的適用性。

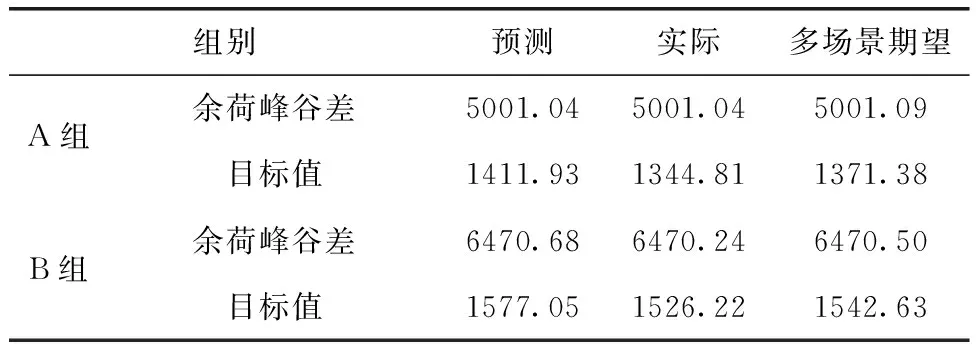
表2 調峰結果指標統計 MW

圖6表示A、B兩組在不同場景下的調峰效果情況，從圖中可以看出，其預測結果與實際結果沒有顯著差異。表明處于三種場景下水電對實際凈負荷調節之后的余荷峰谷差減小率沒有顯著區別。與單場景預測進行對比，發現處于多場景期望模型下的水電調峰過程與實際場景下的出力過程更為相似。同時也能表明所提出的考慮凈負荷不確定性的水電站日前調峰模型的有效性和適用性。試驗采用Kmeans算法對某地區某月的風功率場景進行聚類，場景之間存在著顯著差異，調度結果也驗證了聚類結果的有效性；本文構建的考慮凈負荷的調峰模型主要通過多場景方法描述了由風電出力的不確定性引起的水電凈負荷的不確定性，該方法增加了模型的魯棒性的同時也能降低因風電不確定性導致的水電錯位調峰風險。由此可證明，本文所提出的模型在考慮凈負荷不確定性的梯級水電站日前調峰的應用上具有重要的實際意義。

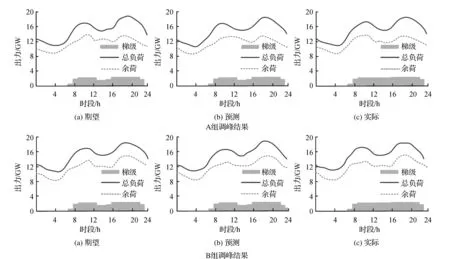
圖6 A、B兩組調峰結果圖

3 結 論

為了改善凈負荷不確定性的梯級水電站日前調峰問題，研究提出一種考慮凈負荷不確定性的梯級水電站日前調峰模型。針對此模型，試驗選取了某地區某月兩日不同預測和實際風電出力過程，首先，對其單場景風功率的調峰結果進行分析，試驗結果表明，實際結果與預測結果都存在一定的誤差。隨后采用Kmeans算法對顯著差異的不同場景進行聚類，驗證了聚類結果的有效性。試驗針對風功率引起的凈負荷不確定性的試驗結果顯示，所提模型能夠充分描述該地區該月關于風電出力的不確定性，且顯示出現的概率分別為14%、33%、30%、27%。試驗構建的模型通過多場景的方法來描述由風電出力的不確定性而引起的凈負荷不確定性，在一定程度上增加了模型的魯棒性，降低了水電錯位調峰的風險。本次試驗所提出的模型在考慮凈負荷不確定性的梯級水電站日前調峰方面具有廣闊的應用前景，基本達到了試驗目的，未來可考慮擴展不確定性因素的范疇以展開進一步研究。