基于交互多模型的機動目標定位濾波方法

任雪峰,張卓偉,胡 喆

(1.海裝上海局駐南京地區第二軍事代表室,南京 211153;2.中國船舶集團有限公司第八研究院,南京 211153)

0 引 言

在多平臺雷達系統中,利用多個觀測雷達獲取的位置和速度信息可以對高機動目標進行無源雷達協同定位。無源雷達協同定位技術因其隱蔽性好、探測距離遠等優點,已成為海上無源定位常用的技術之一。傳統的最小二乘擬合定位方法[1]和標準卡爾曼濾波[2-3]定位方法無法滿足高動態條件下無源定位的需求,而交互多模型[4]由于可以在目標運動過程中對目標的運動狀態進行預測,從而自適應改變定位的匹配模型,因此在高機動目標定位中有較好的應用前景。

王剛等[4]采用慣導輔助推算目標的運動狀態,分析高動態條件下的衛星導航運動模型,在高動態條件下取得了更好的定位性能。馮濟洲[5]針對交互多模型算法在目標跟蹤實際運用時所出現的一些問題,在線性與非線性條件下對交互多模型算法進行了改善,實現了對高機動目標準確有效的跟蹤濾波。茅玉龍等[6]分析了對典型運動目標雙站協同測距理論的定位精度,具體給出了提高雙站定位精度優化算法的計算機仿真結果,完善了高機動目標定位濾波方法。王康[7]針對水下環境,在線性高斯動態系統中采用交互多模型卡爾曼濾波算法對水下機動目標進行跟蹤定位,大大提高了水下高機動目標跟蹤性能。在現有的定位技術中,一般僅通過標準卡爾曼濾波方法對高機動目標的航跡數據進行濾波,難以獲得較高的定位精度。

本文提出一種基于交互多模型的高機動目標定位濾波方法,并將其應用于無源雷達的定位算法中。首先給出幾種常見的運動模型,并介紹交互多模型算法的基本原理;然后圍繞交互多模型算法在高機動目標定位中的具體應用,對算法做進一步推導;最后在幾種運動條件下對算法進行仿真。

1 高機動條件下的目標模型

按定位需求可以將高機動目標的運動狀態分為3種運動模型的組合:勻速直線模型、勻加速運動模型、轉彎模型。

1.1 勻速直線運動模型

目標勻速直線運動的運動狀態可以用CV模型表示為

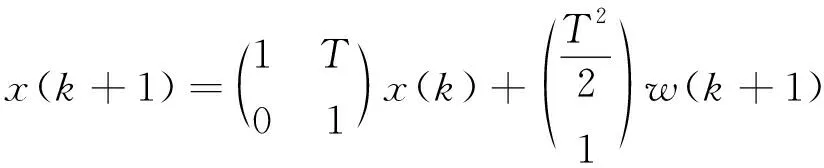
(1)

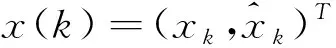
1.2 勻加速直線運動模型

目標勻加速直線運動的狀態可以用CA模型表示為

(2)

式中:T為時間間隔;x(k)=(xk,xk1,xk2)T為目標的狀態向量,xk為位置信息,xk1為速度信息,xk2為加速度信息;w(k+1)為噪聲向量,是服從均值為0、方差為σ2的高斯分布。

1.3 轉彎運動模型

假設目標的轉彎角速度為ω,則目標轉彎運動的運動狀態可以用CT模型表示為

(3)

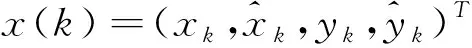
2 基于交互多模型的高機動目標定位濾波方法

在較為清楚目標的運動規律時,一般通過建立特定的運動模型來描述目標的運動狀態,但目標機動時的運動過程往往很復雜,單一運動模型不能很好地與目標真實的運動狀態相匹配,而交互多模型通過多種運動模型來描述目標的運動狀態,克服了單一運動模型的缺陷。在工程應用中,常常采用標準卡爾曼濾波模型實現目標航跡數據濾波,但濾波效果不太理想。無跡卡爾曼濾波算法通過非線性模型對非線性函數的概率密度分布進行近似,濾波效果通常比標準卡爾曼濾波模型更好。

2.1 標準卡爾曼濾波模型

標準卡爾曼濾波模型的觀測方程和測量方程為

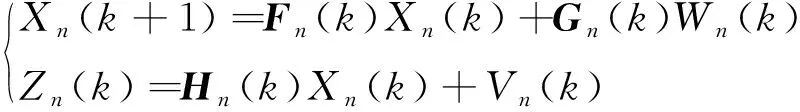
(4)

式中:Xn(k)為第n個模型第k時刻的狀態向量;Fn(k)為第n個模型第k時刻的狀態轉移矩陣;Gn(k)為第n個模型第k時刻的過程噪聲驅動矩陣;Wn(k)為均值為0、協方差矩陣為Qn的白噪聲序列;Zn(k)為第n個模型第k時刻的觀測向量;Hn(k)為第n個模型第k時刻的觀測矩陣;Vn(k)為均值為0、協方差矩陣為Rn的白噪聲序列。

2.2 無跡卡爾曼濾波模型

無跡卡爾曼濾波模型的觀測方程和測量方程為

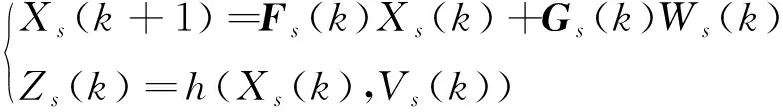
(5)

其中h是非線性觀測方程函數。

2.3 基于交互多模型的目標定位濾波算法

基于交互多模型的目標定位濾波算法具體流程如圖1所示。

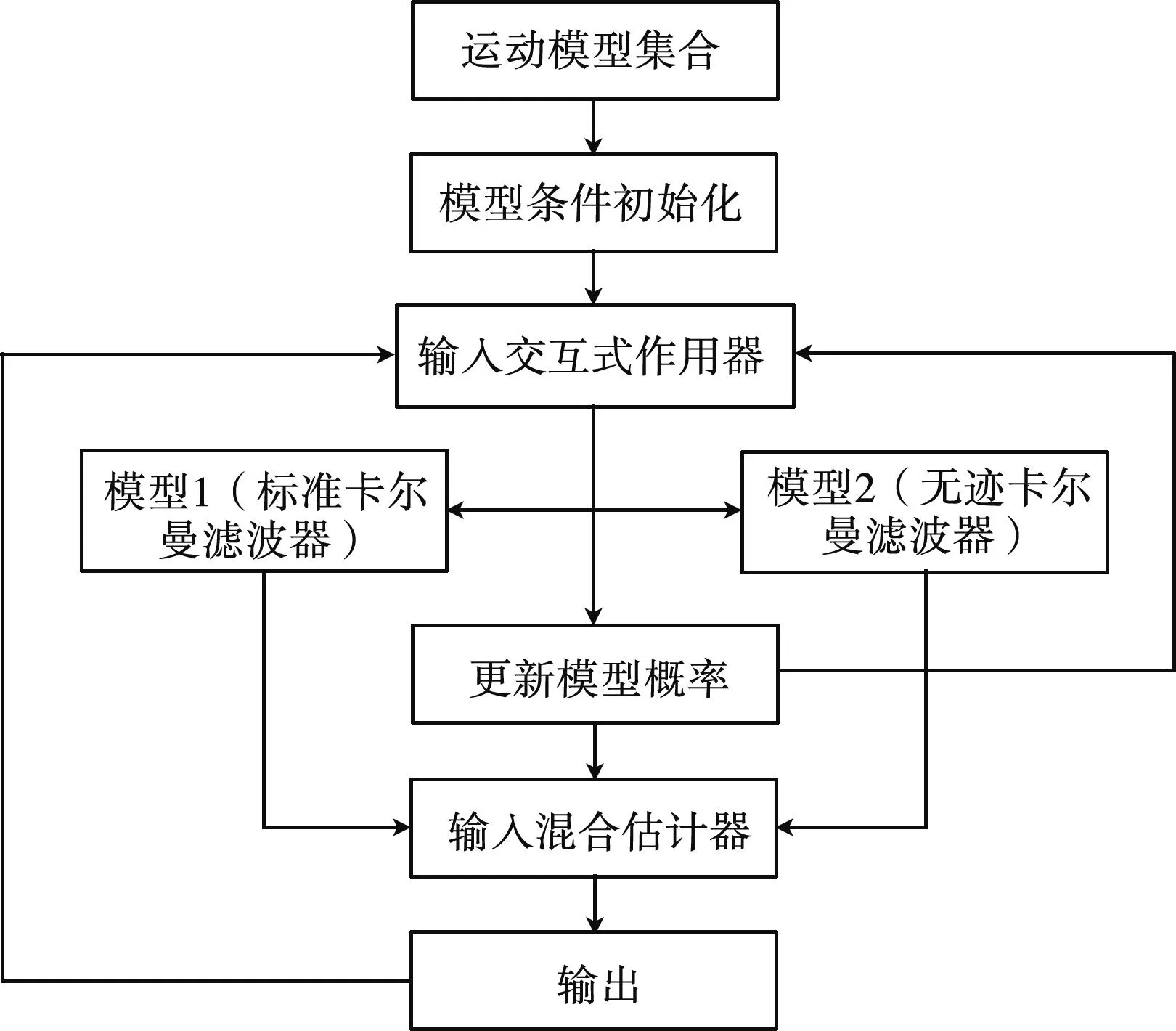
圖1 交互多模型定位濾波算法流程

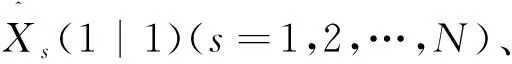
模型n預測概率(歸一化常數)為

(6)

模型m到模型n的混合概率為

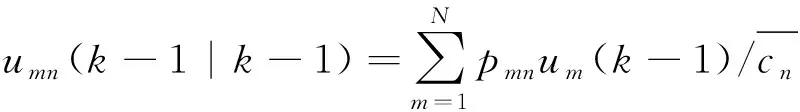
(7)

式中:pmn為模型m到模型n的轉移概率。

模型n的混合狀態估計為

umn(k-1|k-1)

(8)

模型n的混合協方差估計為

{Pm(k-1|k-1)+

(9)

(10)

對P0n(k-1|k-1)進行一步預測,得到k時刻模型n的誤差協方差先驗估計:

Pn(k|k-1)=Fn(k)P0n(k-1|k-1)Fn(k)T+

Gn(k)QnGn(k)T

(11)

計算卡爾曼增益:

Kn(k)=Pn(k|k-1)HT×

[HPn(k|k-1)HT+Rn]-1

(12)

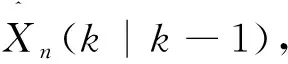
(13)

得到更新后的誤差協方差先驗估計:

Pn(k|k)=[I-Kn(k)H]Pn(k|k-1)

(14)

3 實驗仿真

為了驗證本文算法對機動目標的定位效果,在MATLAB中針對不同的跟蹤場景開展仿真實驗。

(1)一般機動目標

假設雷達對一個在二維平面上運動的一般機動目標進行觀測,目標初始坐標為(2 000 m,10 000 m),初始狀態為在y軸方向具有初始速度vy=15 m/s,具體運動參數如表1所示。

表1 一般機動目標的運動參數

整個運動過程歷時700 s,雷達采樣間隔為1 s,測距誤差為100 m,蒙特卡洛次數為100次,采用交互多模型濾波算法對目標進行跟蹤。交互多模型針對不同的運動狀態采用3個濾波模型,模型的噪聲方差q分別為0、0.01、0.09,模型先驗概率分別為1/3、1/3、1/3,模型轉移概率矩陣為

使用基于交互多模型的濾波算法對一般機動目標進行定位,目標的真實軌跡、濾波跡線和量測點跡結果曲線如圖2所示。可以看出:經過濾波得到的估計曲線基本上在真實軌跡附近,無論是直線運動還是轉彎運動階段,都能相對較好地完成目標定位,達到較好的濾波結果。

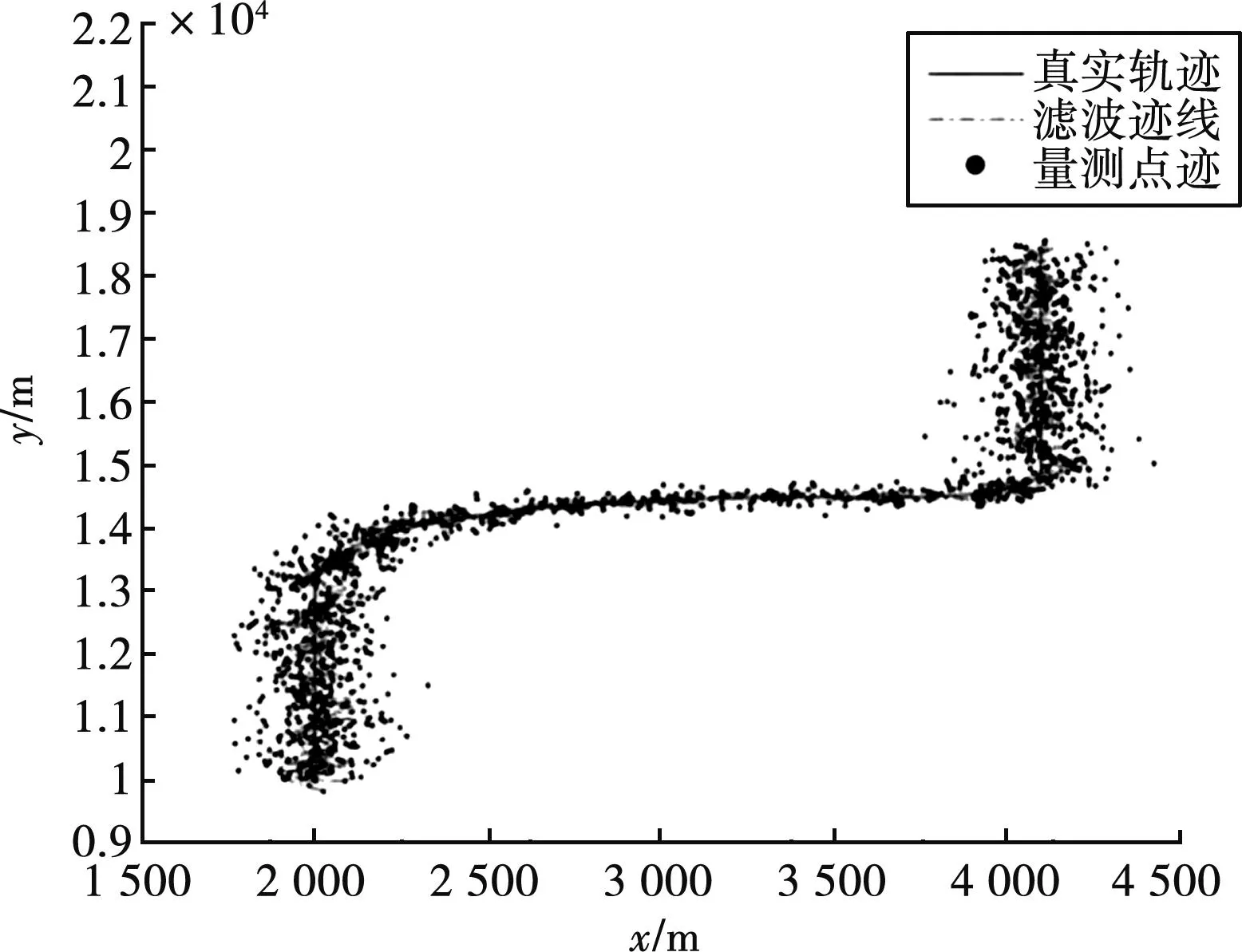
圖2 本文算法對一般機動目標的定位效果

(2)高機動目標

假設雷達對一個在二維平面上運動的高機動目標進行觀測,目標初始坐標為(38 480 m,12 000 m),初始狀態為在x軸方向具有初始速度vx=-426 m/s,具體運動參數如表2所示。

表2 高機動目標的運動參數

整個運動過程歷時85 s,雷達采樣間隔為1 s,測距誤差為100 m,蒙特卡洛次數為100次,采用交互多模型濾波算法對目標進行跟蹤。交互多模型針對不同的運動狀態采用3個濾波模型,模型的噪聲方差q分別為0.01、10、100,模型先驗概率分別為1/9、4/9、4/9,模型轉移概率矩陣為

使用基于交互多模型的濾波算法對高機動目標進行定位,目標的真實軌跡和量測點跡結果曲線如圖3所示。可以看出:本文算法能夠較好地擬合高機動目標的運動軌跡,在加速度較小時與真實軌跡的誤差幾乎為零,在機動目標運動狀態發生急劇變化時也能及時調整,從而達到較好的濾波效果。

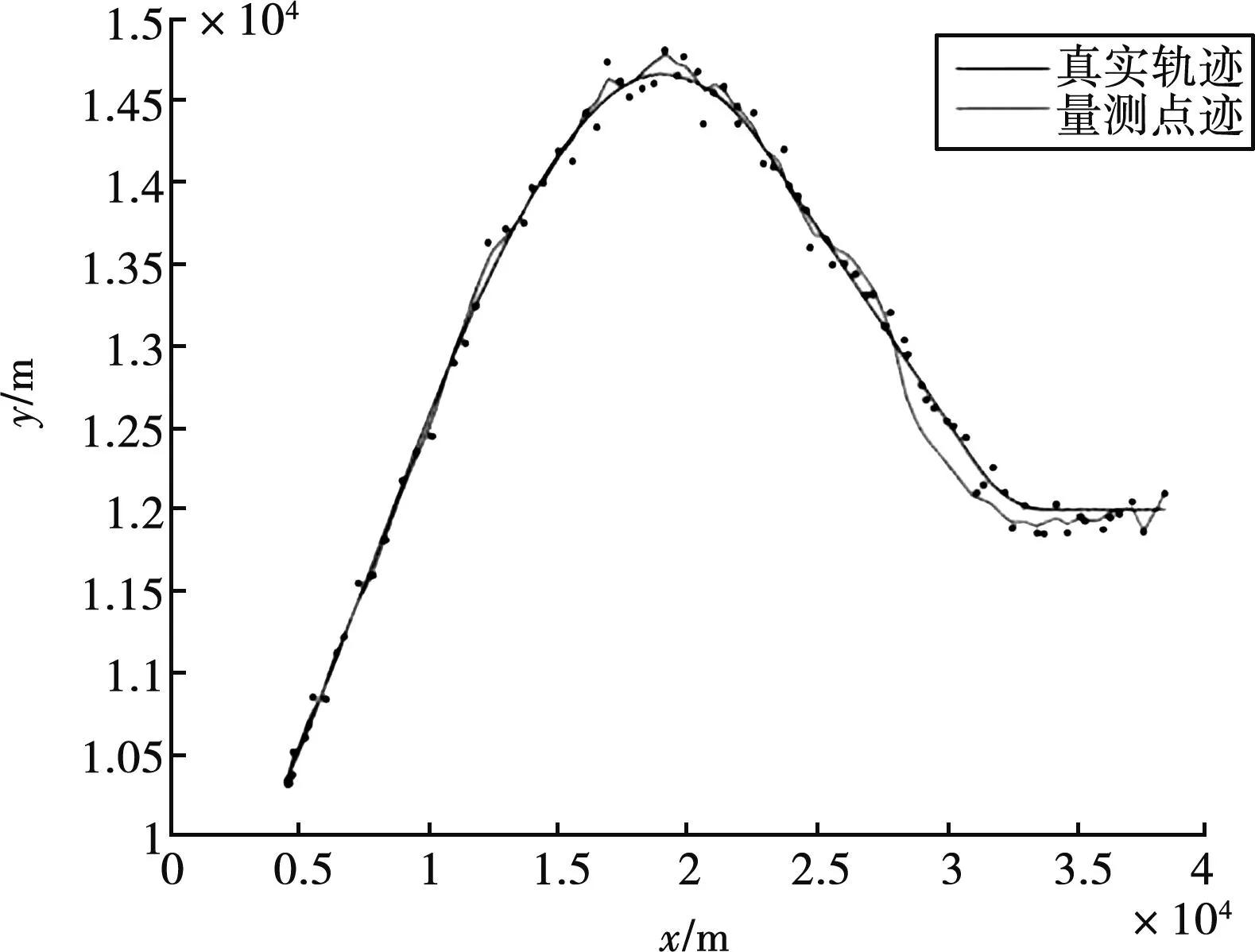
圖3 本文算法對高機動目標的定位效果

(3)定位誤差對比實驗

為了進一步驗證本文算法對高機動目標的定位效果,采用最小二乘擬合法作為對比算法,在相同的實驗條件下開展實驗,結果如圖4所示。可以看出:隨著跟蹤步數的增加,在高機動情況下最小二乘擬合法和本文算法的定位誤差均逐漸收斂,且相應的收斂值均小于雷達的測距誤差,這說明兩種算法都可實現對高機動目標的跟蹤。但本文算法的定位誤差在目標的整個運動過程中保持平穩且維持在較低水平,因此跟蹤精度優于最小二乘擬合法,更適合高機動目標定位。

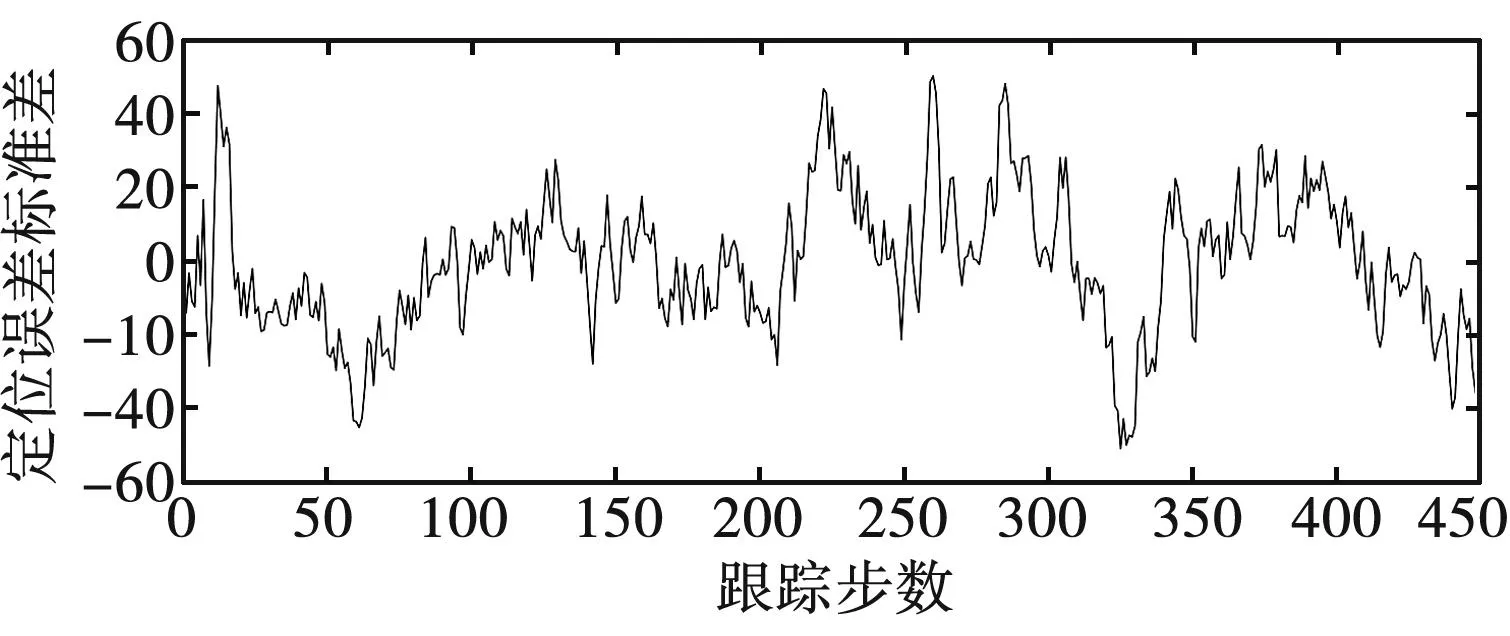
(a)最小二乘擬合法定位誤差

4 結束語

本文提出一種基于交互多模型的高機動目標定位濾波方法。交互多模型算法通過多個運動模型描述目標的運動狀態,利用有效的加權融合進行系統狀態估計,一定程度上克服了單運動模型估計誤差較大的問題。仿真結果表明:本文算法能夠較好地擬合高機動目標的運動狀態,與其他算法相比定位誤差較低,能夠滿足無源雷達對于高機動目標定位的需求。