多能互補模式下水電機組AGC 邊界與轉輪疲勞影響研究

周 葉

（北京中水科水電科技開發有限公司，北京 100038）

0 前言

近年來，隨著風光等隨機能源大規模接入，水電的運行方式由獨立“供能”運行向多能互補模式“調能”運行轉變。與傳統“供能”水電機組相比，“調能”水電機組通過中低負荷區大幅度快速調節和低負荷區小幅度快速調節兩種特殊運行方式以保證電網頻率穩定。需要注意的是，這兩種運行方式需要頻繁觸發水電機組調速系統的一次調頻和AGC 控制，期間引發的水力振蕩、機械振蕩和電力振蕩相互耦合振蕩，進一步增大了水電站在暫態過渡過程中的運行風險，加劇了轉輪疲勞損傷[1]。

轉輪作為水輪機核心部件之一，關系到整個機組、甚至水電站的安全穩定。水輪機運行過程中，轉輪葉片承受旋轉帶來的離心力和強烈的壓力脈動，尤其水輪機在處于偏工況運行時，這種現象更為劇烈[2]機組各部件之間頻繁的相互作用，也會對機組運行產生潛在危害，特別是對于部分投入運行較長時間的機組，大部分水力運行條件已經有了顯著差別，當負荷頻繁發生變化時，機組的振動會導致轉輪出現疲勞裂紋甚至破壞，裂紋的產生和擴展可能導致轉輪等關鍵部位過早損壞或失效，檢查和修復疲勞引起的破壞會造成更大的經濟損失。因此，必須解決或預防疲勞問題，確保機組在設計壽命安全穩定運行。

本文以系統最大化滿足目標負荷曲線與最小化水電機組的總耗水量為目標，建立多能互補模式下水電機組AGC 邊界優化模型；其次，對水電機組進行流固耦合計算與應力分析，研究機組在全工況快速調節下水力波動、軸系擺度和功率振蕩的動態演化規律，評判轉輪疲勞影響；最后，利用核密度估計法分析風光預測誤差導致的出力不確定性，選出典型風光場景并進行模擬分析，提出多能互補模式下水電機組AGC 邊界與轉輪疲勞影響評價方法。

1 水風光互補模式下水電機組AGC 邊界模型

1.1 AGC 邊界優化過程

為保證水風光多能互補運行模式可靠性和經濟性，需要對風電和光電出力的不確定性進行建模。現有研究表明，風電和光電出力的不確定性與其出力水平有關，出力水平越高，其預測誤差越大。極大的預測誤差會導致系統的功率不平衡和頻率波動，威脅系統安全穩定運行。

因此，通過核密度估計分析風光預測誤差導致的出力不確定性，并推導不確定性導致的系統頻率波動偏差約束來精確量化水電機組AGC 邊界，流程如圖1 所示。

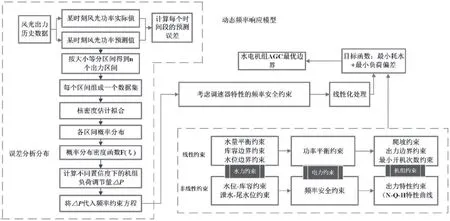
圖1 水風光多能互補模式下水電機組AGC邊界優化結構框圖

1.2 多機組頻率響應過程

對多水電機組的電站而言，其動態頻率響應過程主要跟△P有關。由圖2 可以看出，△Pm又與頻率偏差和機組的傳遞函數G有關。

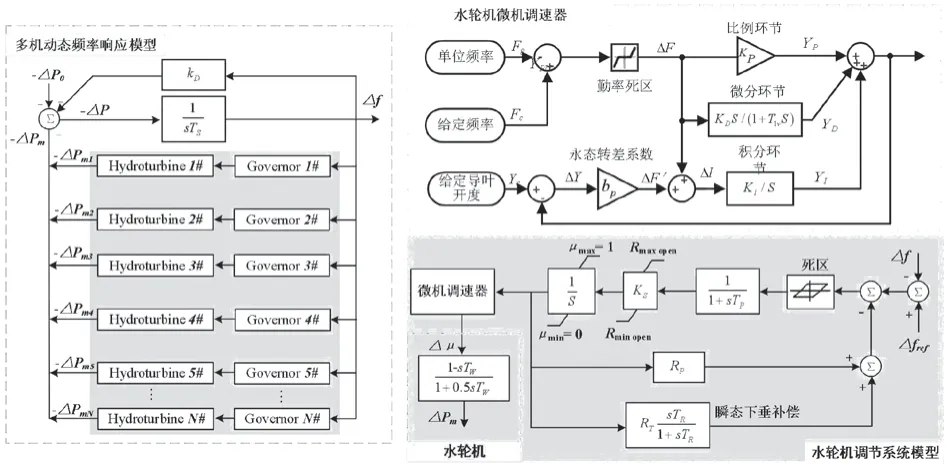
圖2 考慮調速器特性的多水電機組頻率響應模型

傳遞函數表達式比較復雜，很難推導其準確的解析式。因此本文主要關注功率擾動后系統頻率偏差的極限值，用一階慣性環節近似代替水輪機調節系統傳遞函數來模擬水電多機系統的動態頻率響應過程。可表示為：

其中和分別為機組i 的工頻特性系數和發電機，調速器和水輪機的綜合時間常數。結合式子（1）可得到水電機組出力變化隨時間的解析式為：

其中為系統總慣性，由機組慣性時間常數和系統內并網的機組臺數決定。綜上所述，將tm帶入式（2）即可得到系統頻率響應靈活性供給為：

1.3 目標函數

在風光出力不確定性量化的基礎上，多能互補運行模式下水電機組AGC 邊界優化模型的目標函數包括兩個，其一是保證系統最大化滿足目標負荷曲線，其二是最小化水電機組的總耗水量。將兩個目標函數通過權重因子組合，目標函數可表示為：

其中Kp和Kq分別為兩個目標的權重系數；和分別為t時段系統超出和低于目標負荷的松弛變量；為水電系統總下泄流量；γP-Q為從MWh 到m3/s 的單位轉換因子；Qi，t為第i 臺機組t時段流量，單位為m3/s；為t時段電站棄水流量，單位為m3/s；I為水電機組集合；T為時段集合；△t為每個時段時長，單位為h。

2 轉輪疲勞損傷研究方法

轉輪的結構疲勞可分為裂紋萌生與裂紋擴展兩種表現形式[3]，是機組壽命減少的主要原因，通過應力測量的方式可以獲得轉輪應力變化情況：

式中，σ為應力，MPa；E為彈性模量，單位為MPa；ε為應變，單位為mm。

在采集到機組應變數據后，通過雨流計數法對應力變化進行統計分析，將隨機荷載圖轉化為數個全循環，從而進行疲勞壽命計算—Minner 線性累計損傷理論：Palmgren-Miner 線性累積損傷理論是一種以線性方法來計算累積損傷的理論，在工程上因其便利性被廣泛應用。當i 個不同來源的應力貢獻之和D 等于1 時，即發生疲勞破壞[4]：

式中，N 為某應力下被破壞所需要的循環次數，n 為已經歷過的循環。

在得到應力大小與循環次數后，參考轉輪疲勞特性曲線，即材料的應力-壽命曲線（S-N 曲線[5]），采用線性累積損傷Miner 法則，該方法用于脆性材料的高周疲勞預測，示意圖如圖3 所示。

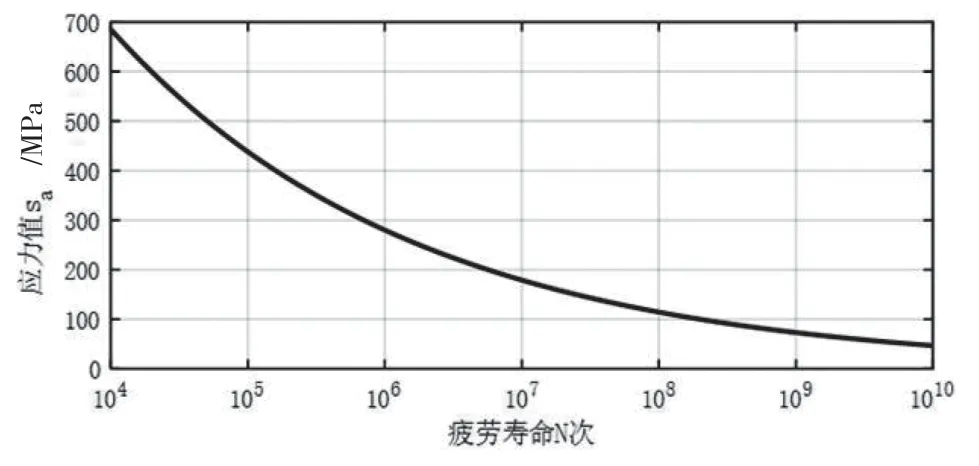
圖3 材料結構疲勞特性曲線

3 實例分析與研究

3.1 多能互補系統水電機組AGC 邊界優化

圖4 為案例地區一年365 d 的風速數據。橫坐標為風速和負荷的斯皮爾曼相關系數，縱坐標為表示實測風速和預測風速的均方誤差MSE，圓圈的顏色代表季節，圓圈大小表示當日風速平均值。可以看出，在斯皮爾曼系數為-0.75 附近和0.75 附近數據點比較集中，在-0.5～0.5 間數據點較為分散。數據的均方根誤差（MSE）值集中在0～0.5 區間范圍內，占總數的80%。季節和均值未表現出與斯皮爾曼系數和MSE 的明顯關系。風速和風電出力是正相關關系，而風電出力與負荷需求高度相關是對系統最有利的情況，因為在這種情況下系統的凈負荷波動是最小的，常規機組可以保持相對平穩的出力。而MSE 值越大則表示風速預測出現了較大的偏差，這會給日前機組組合安排帶來相當大的困難，意味著樂觀的置信度選擇可能會導致靈活性不足的情況。

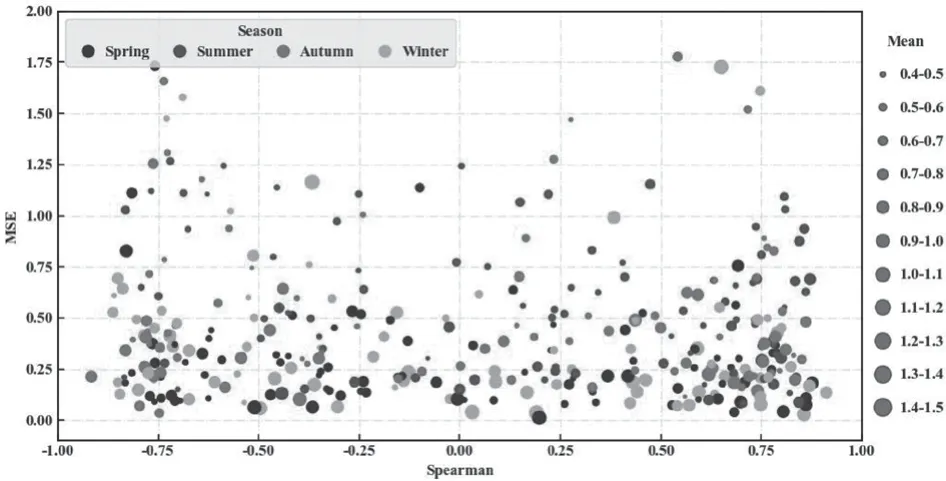
圖4 風電出力場景與負荷的相關性及波動性分析

優化求解獲得6 臺機組在每小時AGC 邊界圖表2 所示，可以發現每臺機組的出力情況都在最大與最小出力之前，且機組的運行和停止時間在最小啟停間隔時間內，符合約束要求。最終優化結果為耗水量最小值為1.68e+05 m3/s，GAP 值為3.11%。

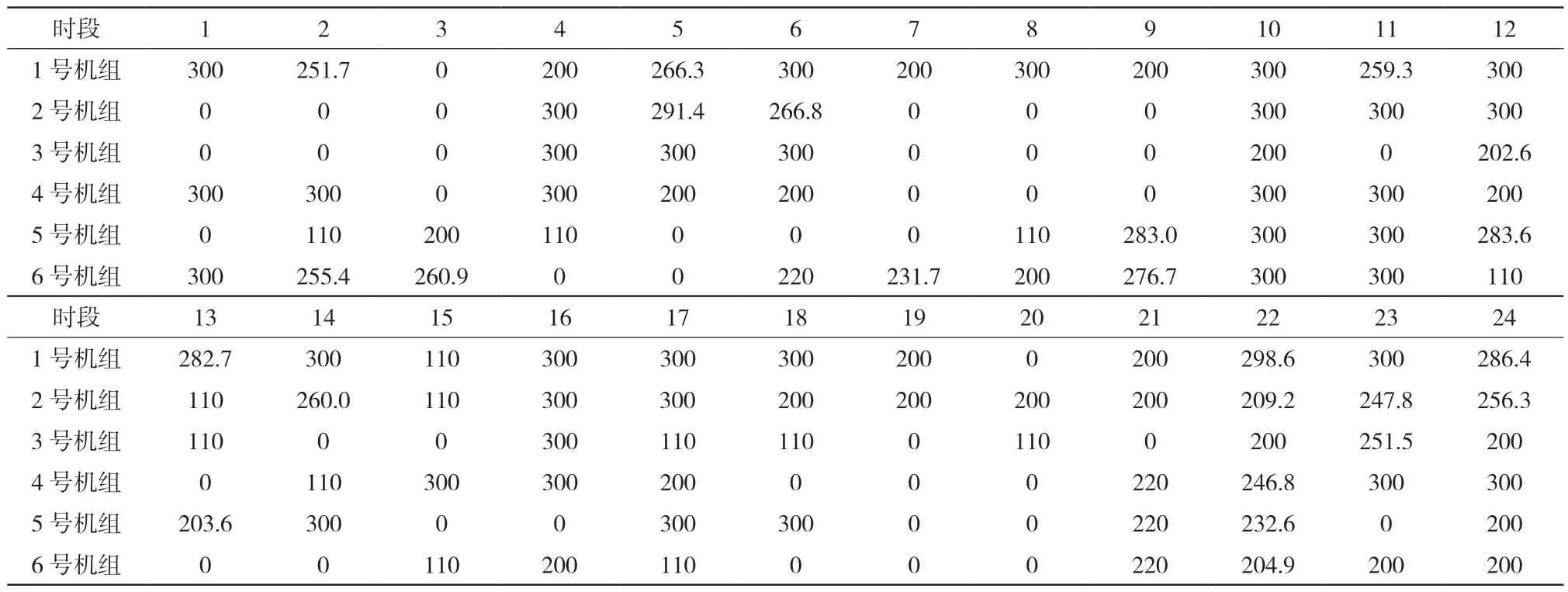
表2 多能互補系統水電機組AGC 邊界優化結果

圖5 展示了不同負荷（LVH）和風光裝機容量（WVH）配比下水電機組AGC 邊界優化模型的最小置信度選取建議。其中NS 符號代表在此配比下模型不可解，UQ 代表模型在部分置信度下可解，但所有結果均無法滿足頻率需求，90*代表模型所有置信度可解，但即使取到90%置信度仍有部分時段頻率限制超出范圍，其余數字代表在該配比下可以全時段滿足頻率波動限制的最小置信度。可以看出在負荷水平較高或風光滲透率較低的情況下第置信度即可滿足多能互補系統的頻率可靠性要求，而在風光滲透率較高的情況下的最小推薦置信度較高，說明此時系統中風光出力的不確定性對系統可靠性威脅更大。調度人員可參考不同配比下的推薦置信度來制定水電機組AGC 邊界，或根據不同的置信度需求在日前決定風光、水電和負荷的配比來保證多能互補系統的經濟可靠運行。

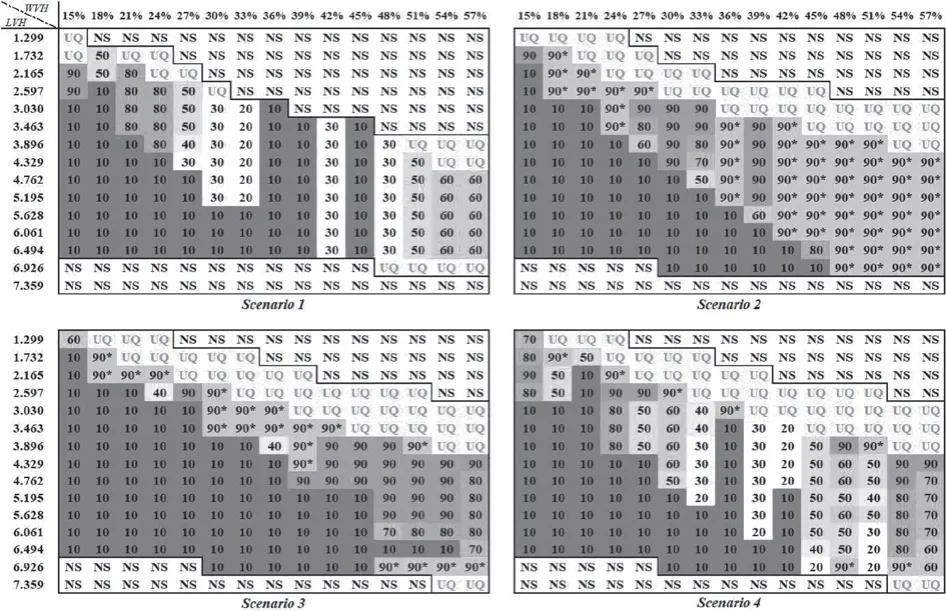
圖5 不同配比下水電機組AGC 邊界優化模型的最小置信度選取建議

3.2 轉輪疲勞評估

為更準確得到轉輪易發生疲勞損傷及破壞的位置，根據表2 和圖5 結果，對某水電站3 號水電機組轉輪進行流固耦合計算，得到一段運行時間內轉輪上的變形、應力值及其變化范圍，轉輪上等效應力、總變形分布如圖6 所示。

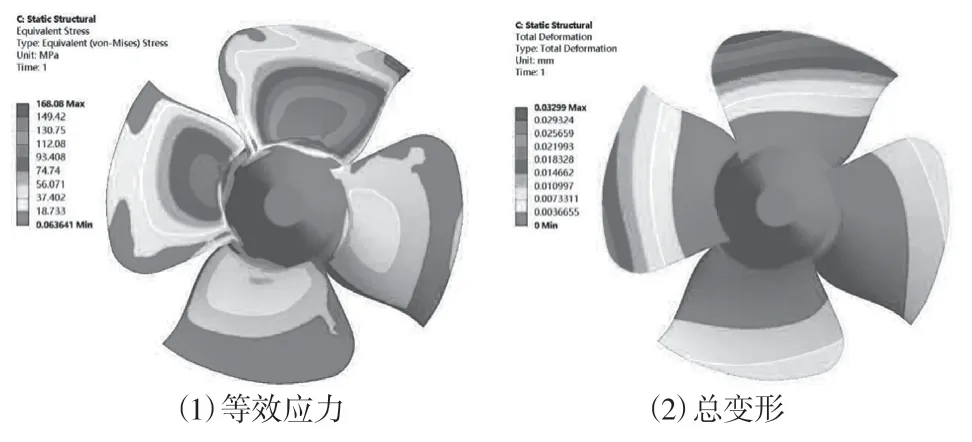
圖6 轉輪等效應力及應變

由圖6（1）可知，整體上看，應力主要分布在葉片及葉片與轉輪連接區域，主要應力范圍在0.06～168.08 MPa。由于水流沖擊及葉片構造，靠近葉片根部所受力矩最大，在葉片根部與轉輪連接處出現應力集中，因此最大應力值出現在葉片根部，其最大應力為168.08 MPa。也就是說，在葉片根部更容易萌生裂紋，并在不斷的交變應力下擴張，最終造成轉輪和葉片的疲勞破壞。總變形為應力的外在表現形式，如圖6（2）所示，葉片變形量為0～0.03 mm。可以看到所有葉片變形位置出現在輪緣頂端，最大值為0.03 mm。變形量隨半徑減小而減小。結合來看，最大變形的葉片，應力也最大，因此在實際水輪機運行過程中要將應力最大處作為危險點進行監測。

為判斷危險點是否會發生疲勞破壞，通過雨流計數法對收集的應力數據進行處理，如圖7 所示。可以看到應力均值主要集中在50～70 MPa，且主要循環次數集中在60～120 次之間。在不同負荷情況下，疲勞損傷累計如圖8 所示，可以看到1 000 h 內，40～80 MW 與140～180 MW 的負荷下，疲勞損傷值最大，120～140 MW 與180～250 MW 負荷下的疲勞損傷之最小。這與機組頻繁穿越振動區有著一定的關聯，但最主要的原因還是在于葉片構造與機組形狀有較大關聯。

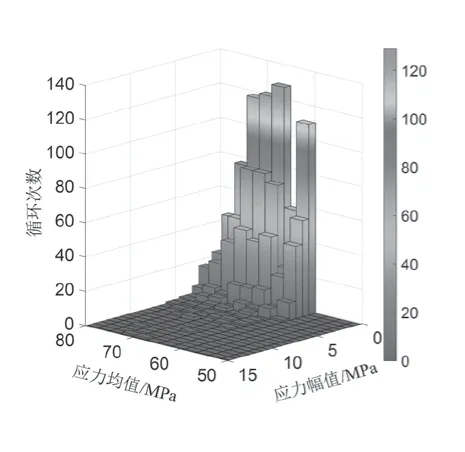
圖7 雨流計數結果

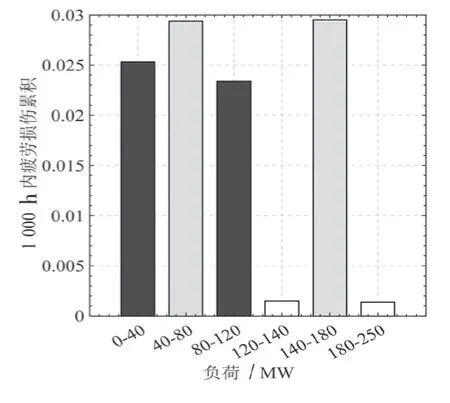
圖8 疲勞損傷累計示意圖

4 結語

本文針對多能互補模式下水電機組由傳統“供能”轉向“調能”的安全高效運行問題，其研究目標為揭示水力機組全工況快速調節AGC 動態邊界與轉輪疲勞影響。通過突破風光不確定性量化分析與機組頻率安全約束，建立水風光多能互補模式下水電機組AGC 邊界優化模型；開展“調能”機組在全工況快速調節下水力波動、軸系擺度和功率振蕩的動態演化規律研究，探討轉輪疲勞影響評價方法；最后，提出水電機組優化AGC 動態邊界與轉輪疲勞影響評價方法，為后續多能互補模式下“調能”水力機組的安全穩定高效運行提供重要科學指導。