可變形式翼型鈍體的風致振壓電俘能器

張忠華，李 哲，孟凡許，王淑云，李 赫，闞君武

（浙江師范大學 精密機械與智能結構研究所，浙江 金華 321004）

1 引言

隨著微功率便攜式電子產品和無線傳感器節點的自供電需求越來越高，尋求一種可持續、安全穩定的俘能技術成為了國內外學者討論的熱點話題，為此人們對以電磁、摩擦、壓電等原理為基礎的俘能器進行了多方面的研究［1-4］。電磁式適用于高速旋轉環境、摩擦式適用于微表面接觸環境，相較于前兩者，壓電俘能器的優勢在于結構簡單，易集成一體化微機電系統、無電磁干擾及對材料的損耗較小等［5-7］。根據應用領域工作環境中存在能量的不同，壓電俘能器大致可分為風致振式［8］、旋轉式［9］、振動式［10］三類。其中，風致振壓電俘能器主要依靠鈍體受風力影響產生振動激勵壓電陶瓷進行發電，其根據激勵鈍體的結構主要分為三類，分別為單鈍體式、多鈍體式及復合鈍體式，三者各有特色，單鈍體式的研究最為普遍，在此基礎上的多鈍體及復合鈍體式振動特性多樣，已然成為風致振壓電俘能器的研究前沿。

早期，學者們主要研究的是卡門渦街對海洋建筑物的振動損害［11］，但隨著研究的深入，利用單鈍體在這種振動中的特性進行俘能的方法逐漸成為熱點話題。2019 年，Wang 等人［12］通過在風力作用下圓柱殼體所產生的渦振間接激勵殼體內的壓電懸臂梁振動發電，有效避免了環境對發電單元的影響，且最佳負載下的功率可達0.4 mW。2021 年，Liu 等人［13］提出一種順流激勵式Y 型鈍體壓電俘能器，試驗表明半角為60°的Y 型鈍體使俘能器輸出電壓提升了近十倍。2022 年，侯成偉等人［14］將圓柱鈍體渦振式俘能器放在可轉動圓盤上，通過圓盤的導向翼自主調節迎風角度，從而大幅提高了其在多風向環境中的適應能力。綜上，單鈍體式俘能器具有結構簡單、理論基礎深厚的優勢，但由于鈍體單一固定，振動特性幾乎不可調，無法適應多變的環境從而導致發電效率較低。

為改善單鈍體式壓電俘能器的振動特性并提高其發電性能，多鈍體及復合鈍體式應運而生。多鈍體式指兩個及以上獨立存在鈍體共同影響俘能器工作，2021 年，Hu 等人［15］提出了一種由方柱鈍體和梳狀鈍體共同作用的壓電俘能器，相較于單一方柱鈍體，它降低起振風速的同時輸出功率提高了約171.2%；2022 年，Liao 等人［16］在圓柱殼體后方安置了一個矩形定鈍體來改善原有振動特性，實現了小振幅渦振向大振幅馳振的轉變，使其輸出功率達到近2.22 mW；2023 年，Kan 等人［17］提出了一種順流激勵式雙鈍體壓電俘能器，通過下游擋板鈍體擾動上游圓柱鈍體的流場來彌補順流激勵振幅小的缺陷，提升高風速下俘能器的結構可靠性及發電能力。復合鈍體式指在單一鈍體上耦合一種及以上部件來改變俘能器原有的振動特性，2020 年，Wang 等人［18］提出一種不同橫截面的混合鈍體式風致振壓電俘能器，通過調節鈍體中圓柱與方柱的占比以及迎風面形狀改善流固耦合特性，使其最大輸出電壓提高71%；2021 年，該團隊又設計了一種非光滑圓柱鈍體來改變渦振特性［19］，研究表明，不同表面的圓柱鈍體可以增強或抑制系統的振動，以期適用于不同的工作環境。綜上，多鈍體結構或復合鈍體結構能有效改善俘能器的振動特性，降低其起振風速、擴寬工作風速范圍，但這兩類俘能器多數以馳振形式工作，容易造成發電單元的損壞，故其高風速環境下的適應能力還存在提升空間。

除此之外，近幾年還出現了一種可變鈍體式的風致振壓電俘能器，2018 年，Zhou 等人［20］提出利用彎曲機翼的Y 形鈍體所產生的相干共振來提高低速氣流的俘能效率；2020 年，Sun 等人［21］提出一種滑動式圓柱鈍體的風致振壓電俘能器，實現拓寬鎖頻范圍、提高平均功率的目的。綜上，該類俘能器為風能的采集開辟了新方向。

針對上述各類問題并結合現有研究，本文提出一種可變形式翼型鈍體的風致振壓電俘能器，它主要由可變式翼型鈍體（彈性翼+剛性翼）、懸臂梁及壓電組合梁構成，鈍體的彈性翼受風力影響產生形變，從而實現系統振動特性的自我調節，以期達到降低起振風速、拓寬工作風速范圍及限制高風速系統振幅的目的。通過建模仿真和試驗兩種方法研究結構參數（鈍體迎風角和彈性翼剛度）、風速及負載電阻對俘能器輸出特性的影響規律，證明該結構原理能夠提高其環境適應性，為構造滿足自供電需求的俘能器后續研究提供了新思路。

2 俘能器的結構與工作原理

可變形式翼型鈍體風致振壓電俘能器的結構原理如圖1 所示，主要由基座、懸臂梁、墊塊、銅基板、壓電陶瓷、剛性翼及彈性翼組成。其中，墊塊、銅基板和壓電陶瓷三者構成壓電組合梁，并安裝在懸臂梁的兩側，呈對稱分布；剛性翼和彈性翼構成可形變式翼型鈍體，并安裝在懸臂梁的自由端。鈍體的迎風角由兩片剛性翼組成的角度決定，鈍體的形狀則通過彈性翼在風力作用下產生的變形量決定；壓電組合梁自由端的墊塊可實現振動能力的間接傳遞，避免壓電陶瓷因承受超過許用應力的拉應力而損毀［22］。

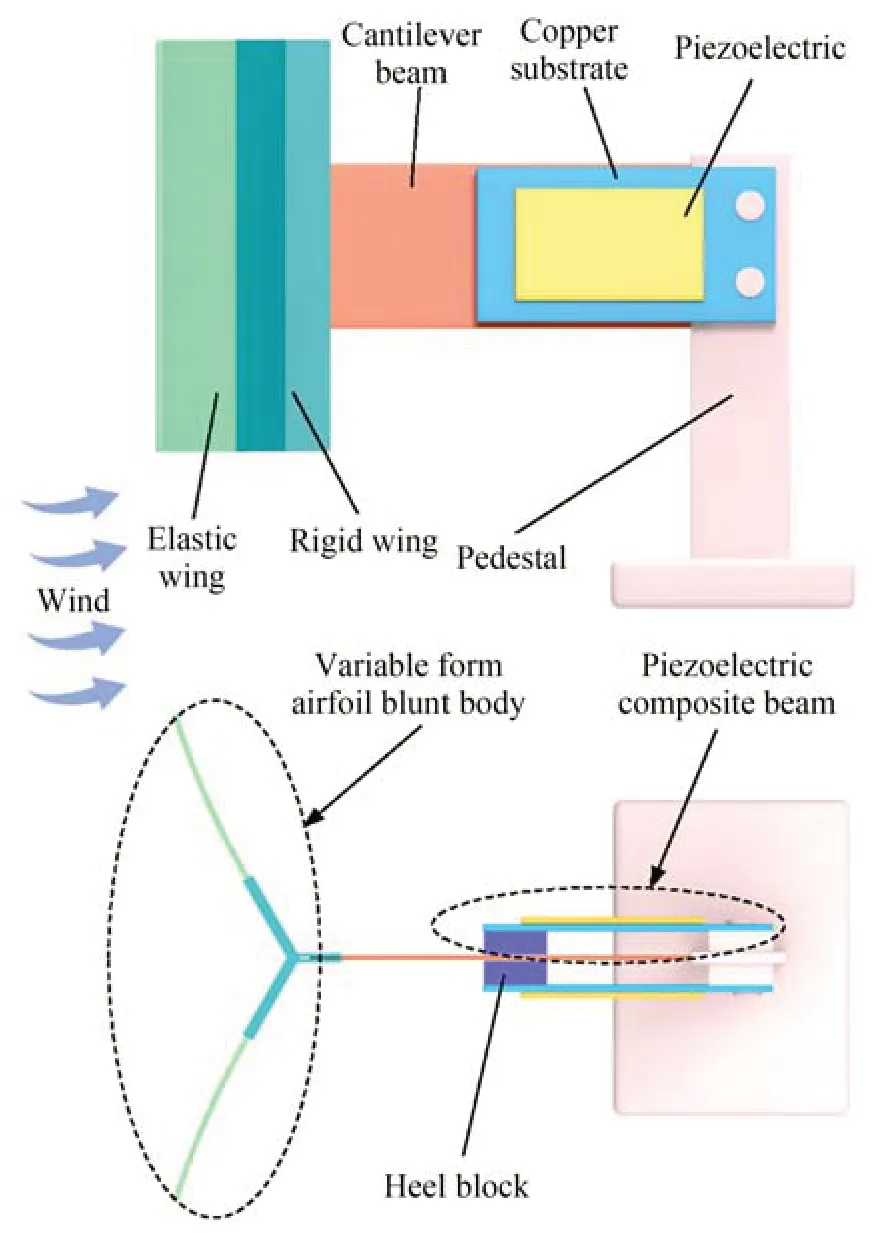
圖1 俘能器的結構示意圖Fig.1 Structure diagram of energy harvester

風致振壓電俘能器主要通過風經過鈍體后在其兩側表面產生的交替漩渦促使鈍體連帶著懸臂梁進行往復擺動，從而間接激勵壓電組合梁變形發電，同時鈍體形狀主要由彈性翼變形量決定，因此可以通過彈性翼受風速影響的大小來改變俘能器的流固耦合及振動特性。為直觀體現出風速對俘能器工作過程及鈍體形狀的影響，采用COMSOL 仿真對其進行了模擬試驗，獲得了俘能器的輸出電壓波形及工作過程，分別如圖2和圖3 所示，其中圖3 是分別在不同風速下提取一個振動周期T內的波峰（0.25T）、平衡位置（0.5T）及波谷（0.75T）的振動形態組成的。根據圖中俘能器鈍體形狀和輸出電壓大小的變化，將工作過程分為兩個階段：

圖2 輸出電壓的波形圖Fig.2 Output voltage waveform

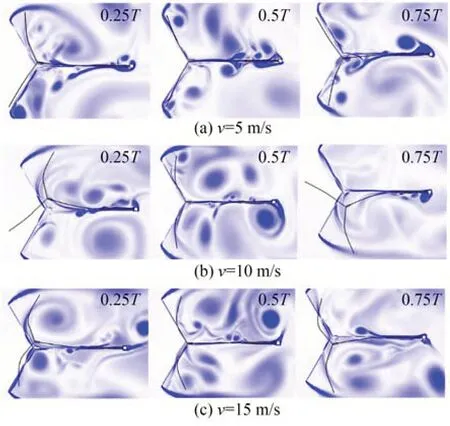
圖3 風速v 不同時俘能器的工作過程Fig.3 Working process of the energy harvester wIth different wind speeds

（1）發散性振動階段：當風速在0～10 m/s 之間時，彈性翼變形較小，鈍體迎風面呈V 字形，其振幅及輸出電壓均隨著風速的增加而增大，結合流體力學理論和現有關于V 型鈍體的研究［13，23］，此時俘能器主要以馳振的方式工作，其中風速v=5 m/s 和v=10 m/s 時的俘能器工作過程分別如圖2（a）和圖2（b）所示；

（2）收斂性振動階段：當風速在10～15 m/s之間時，彈性翼變形較大，鈍體迎風面呈彎弧狀，其振幅及輸出電壓均隨風速的增大而出現減小趨勢，而這種迎風面類似于圓柱鈍體表面的形狀，根據流力力學理論和現有關于圓柱鈍體的研究［24］可知，在這一風速范圍內，俘能器是以類似渦振的方式進行工作，基本實現通過鈍體形狀隨風速變化而變化的特性來防止系統振幅無限制增大的目的，其中風速v=15 m/s 時的俘能器工作過程如圖2（c）所示。

3 有限元建模與仿真

為研究可變形式翼型鈍體迎風角和彈性翼剛度對俘能器的流固耦合特性及輸出性能的影響規律，利用COMSOL 對不同參數下的俘能器進行了模擬仿真，其中由于本文研究重點在于鈍體及其形變狀態，故將壓電組合梁簡化成單層的壓電陶瓷，幾何模型的基本結構參數及材料如表1 所示。

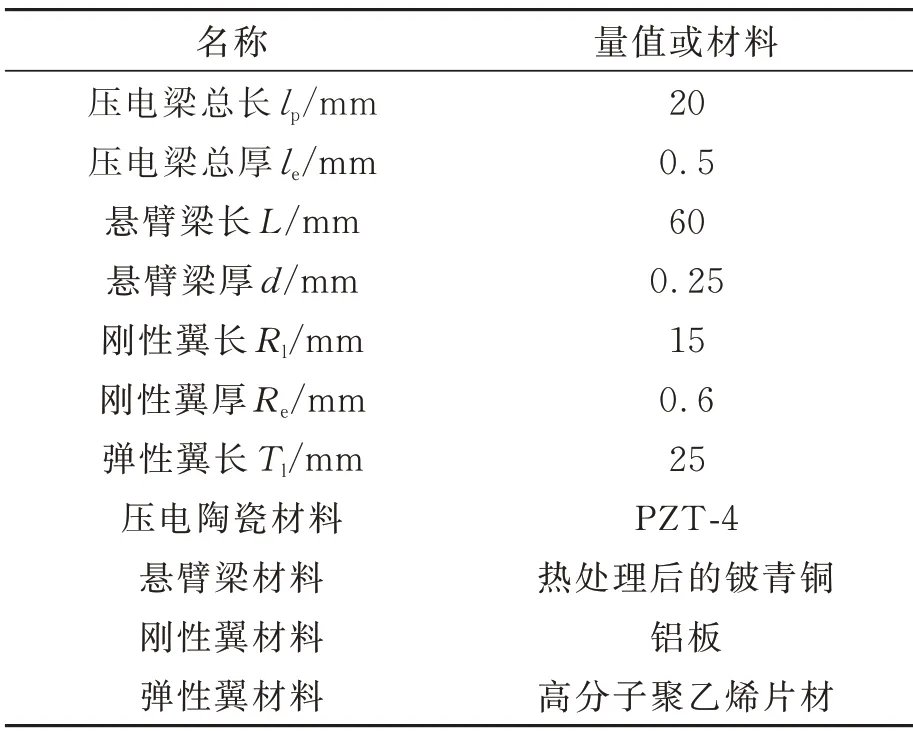
表1 俘能器的基本結構參數及材料表Tab.1 Basic structure parameters and materials of the energy harvester

圖4 為俘能器的幾何模型及流場設置，其中作為變 量的迎風角θ分別為0°，40°，80°，120°，160°及180°；彈性翼剛度因測量不便，將其厚度e作為剛 度變量，其分別 為0.15 mm，0.3 mm，0.45 mm，0.6 mm 及0.75 mm。此外，仿真時采用的測試風速為10 m/s，出口壓力為0 Pa；本文采用寬為鈍體總翼長10 倍（400 mm）、長為其20倍（800 mm）的流場進行測試［25］。

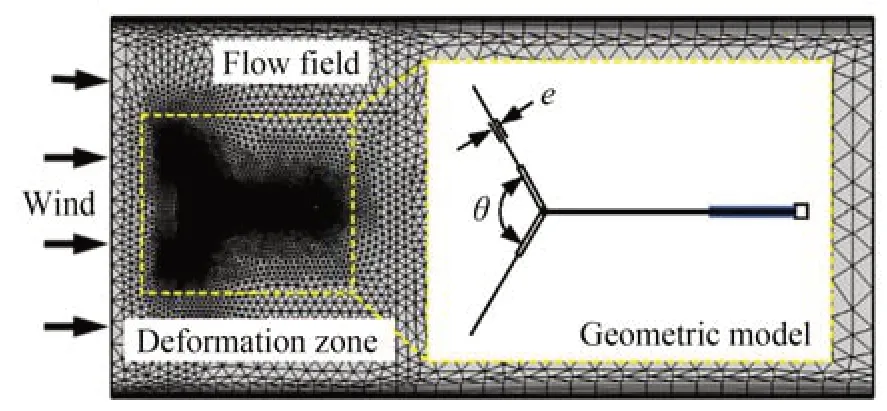
圖4 俘能器的幾何模型及流場設置Fig.4 Geometric model and flow field setting of energy harvester

圖5 為迎風角和彈性翼厚分別作為變量時的風場流速分布及壓力等值線云圖。由圖可知，當θ=0°，e=0.15 mm 時，壓力等值線分布均勻，且鈍體兩側流速基本一致，俘能器無法起振，但隨著θ的增加，俘能器周邊的渦流分布密度和最大壓力差均呈先增大后減小趨勢；當θ=120°、e作為變量時，彈性翼形變量、渦流數量及最大壓力差均隨著e的增大而逐漸增大。

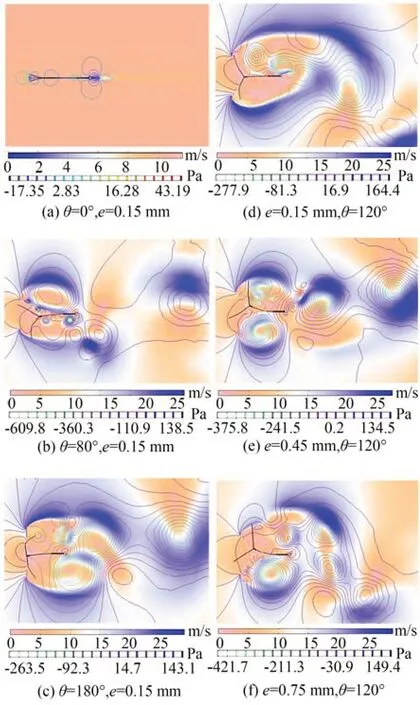
圖5 不同變量下的風場流速分布及壓力等值線云圖Fig.5 Velocity distribution and pressure contour cloud map of wind field under different variables

圖6 為迎風角θ、彈性翼厚e分別作為變量時的輸出電壓波形圖。由圖6（a）可知，當迎風角θ=0°時，由于鈍體迎風面積較小，無法產生交替脫落的渦流促使其起振，但當0°＜θ≤80°時，渦流所提供的壓力差隨迎風角θ增加而增大，故俘能器輸出電壓呈增大趨勢；當80°＜θ≤180°時，由于渦流壓力差及分布密度的減小，俘能器輸出電壓呈小幅下降趨勢。由圖6（b）可知，隨著彈性翼厚e的增加，俘能器輸出電壓會出現小幅上漲，由此表明，降幅的效果隨著彈性翼剛度的增大而減小。綜上，選擇合適迎風角θ和彈性翼厚e能夠實現控制鈍體振幅、有效降低俘能器起振風速及提高發電能力的目的，為后續俘能器的設計、制作和試驗測試提供了理論依據。

圖6 迎風角θ、彈性翼厚e 分別作為變量時的輸出電壓波形圖Fig.6 Output voltage waveform diagram with windward angle θ and elastic wing thickness e as variables respectively

4 試驗測試與分析

為驗證該俘能器結構的可行性及仿真結果的正確性，制作并搭建了如圖7 所示的試驗樣機及測試系統，其結構尺寸和所用材料與仿真基本相同（詳見表1），不同之處在于試驗樣機采用三維結構，其鈍體高度為50 mm，懸臂梁寬度為20 mm，壓電陶瓷的直徑和厚度分別為18 mm 和0.2 mm，銅基板直徑和厚度分別為26 mm 和0.3 mm。試驗所用儀器包括：DS5042M 型數字存儲示波器、測試風機、變頻器、風速儀、電阻箱等。試驗中調節變頻器頻率來間接改變風機的風速，經風速儀測量二者近似呈線性關系（v=0.75f），變頻器步長1 Hz，測試風速范圍為0～25 m/s。試驗中所提到的輸出電壓U均為單片壓電陶瓷的開路峰峰值電壓，輸出功率P為單片壓電陶瓷的峰峰值功率，且主要研究的變量為迎風角θ（0°/40°/80°/120°/160°/180°）和彈性翼厚e（0.15 mm/0.3 mm/0.45 mm/0.6 mm/0.75 mm）。

圖7 試驗樣機及測試系統Fig.7 Test prototype and test system

為驗證不同風速區域內俘能器擁有不同的振動特 性，選取迎風角θ為120°、彈性翼 厚e為0.15 mm 的俘能器進行試驗，獲得了不同振動狀態時的電壓波形及輸出電壓與輸入風速的關系曲線，分別如圖8（a）和圖8（b）所示。由圖可知，俘能器大致有四種振動狀態：

（1）無振區：當風速v在0～3.24 m/s 之間時，輸出電壓微弱，俘能器處于靜止狀態還未起振，產生波形的主要原因為試驗臺的微振動以及示波器內置電壓的干擾；

（2）增幅區：當風速v在3.24～8 m/s 之間時，由于壓電組合梁主要受單向力作用，電壓波形呈周期性非對稱曲線，此時鈍體因風速較小未發生過大變形，整體呈V 型，而根據流體力學理論及現有關于V 型鈍體的風致振壓電俘能器的研究可知，俘能器輸出電壓會隨著風速的增加而快速增大的工作方式，屬于馳振；

（3）等幅區：當風速v在8～17 m/s 之間時，電壓波形與增幅區波形除了幅值外基本一致，俘能器逐漸由馳振轉為渦振，輸出電壓不再隨風速的增加而增大，而是達到最大值后維持在一個小范圍內上下波動，出現近似“鎖頻”的狀態；

（4）降幅區：當風速v在17～25 m/s 之間時，電壓波形的頻率較高但電壓值有所減小，此時鈍體迎風面受強風影響變為彎弧狀，而這種類似于圓柱鈍體表面形狀的鈍體，根據流體力學理論和現有關于圓柱鈍體的風致振壓電俘能器的研究可知，俘能器輸出電壓在某一風速帶內較大，此后會隨風速增大而減小的工作方式，屬于渦振。

圖9 為彈性翼厚e=0.15 mm、迎風角θ不同時輸出電壓U與輸入風速v的關系曲線，圖10 為提取不同迎風角θ下的起振風速v0、鎖頻風速vf（俘能器完全起振并剛進入等幅振動時的風速）、降幅風速vd及等幅電壓Uc構成的規律曲線。由圖9 可知，在試驗風速范圍內，隨著風速v的增加，迎風角θ在0°～80°范圍內的俘能器會出現失穩現象（如圖中A，B，C點所示），即懸臂梁產生過大變形以致偏轉到一邊無法回到平衡位置，而迎風角θ在80°～180°范圍內的俘能器隨風速增大基本會出現無振、增幅、等幅及降幅四種振動狀態，且隨著迎風角θ的增加，等幅振動的風速范圍出現減小趨勢，同時降幅區輸出電壓下降的速率逐漸增大，系統渦振特性愈發明顯。由圖10 可知，在試驗迎風角范圍內，俘能器的起振風速v0隨迎風角θ的增加呈先減小后增大的趨勢；當迎風角θ＜40°時俘能器在起振過程中出現失穩現象，當迎風角θ≥40°時俘能器出現等幅電壓Uc，且其值隨迎風角θ的增加呈波動式下降趨勢，但鎖頻風速vf隨迎風角θ增大呈先減小后增大的趨勢；當迎風角θ＜120°時俘能器基本不會出現降幅現象，而當迎風角θ在120°～180°之間時，俘能器出現渦振特性，且降幅風速vd隨迎風角θ的增加而減小。

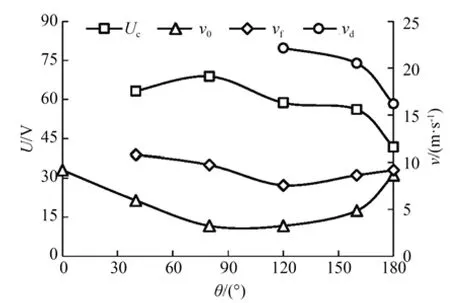
圖10 迎風角θ 對起振風速v0、鎖頻風速vf、降幅風速vd及等幅電壓Uc的影響規律曲線Fig.10 Influence of windward angle θ on vibration velocity，frequency locking velocity，drop velocity and constant amplitude voltage

圖11 為迎風角θ=120°、彈性翼厚e不同時輸出電壓U與輸入風速v的關系曲線，圖12 為提取不同彈性翼厚e下的起振風速v0、鎖頻風速vf、降幅風速vd及等幅電壓Uc構成的規律曲線。由圖11 可知，在試驗風速范圍內，當彈性翼厚e＞0.3 mm 時，俘能器在較高風速下會出現失穩現象（如圖中D，E，F點所示）；當彈性翼厚e≤0.3 mm 時，隨風速增大俘能器均會出現等幅、降幅現象，確保了其結構的安全可靠。由圖12 可知，俘能器的起振風速v0受彈性翼厚e影響較小，但鎖頻風速vf和等幅電壓Uc均會隨著彈性翼厚e的增加而小幅增大，且當彈性翼厚e≤0.3 mm 時，俘能器的降幅風速vd也隨著彈性翼厚e的增加而增大，有效拓寬了其穩定工作的風速范圍。

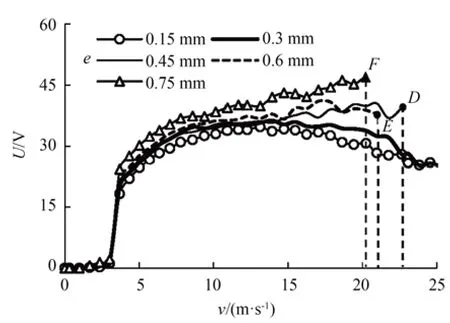
圖11 彈性翼厚e不同時輸出電壓與輸入風速的關系曲線Fig.11 Relation curve between output voltage and input wind speed when elastic wing thickness e is different

圖12 彈性翼厚e 對起振風速v0、鎖頻風速vf、降幅風速vd及等幅電壓Uc的影響規律曲線Fig.12 Influence of elastic wing thickness e on vibration velocity，frequency locking velocity，reduction velocity and constant amplitude voltage

綜上，存在迎風角θ為120°～160°、彈性翼厚e為0.15～0.3 mm 時，俘能器的起振風速較低、工作風速范圍較寬，同時其振幅不會因風速的增加而無限制增大，提高了俘能器的環境適應性，且試驗所獲得的規律與仿真分析結果基本保持一致，證實了仿真模型的正確性。

圖13 為 彈性翼厚e=0.15 mm、迎風角θ不同時輸出功率P與負載電阻R的關系曲線，分別選取三個較為合適的迎風角θ（80°，120°及180°），然后在15 m/s 的風速激勵下通過調整負載電阻找到該俘能器的匹配阻抗，以此獲得它們的最大輸出功率。由圖中可知：存在最佳的負載電阻（250 kΩ）使該俘能器的輸出功率達到最大，當迎風角θ為80°，120°及160°時，俘能器最大輸出功率分別為3.78 mW，2.65 mW 及2.52 mW。

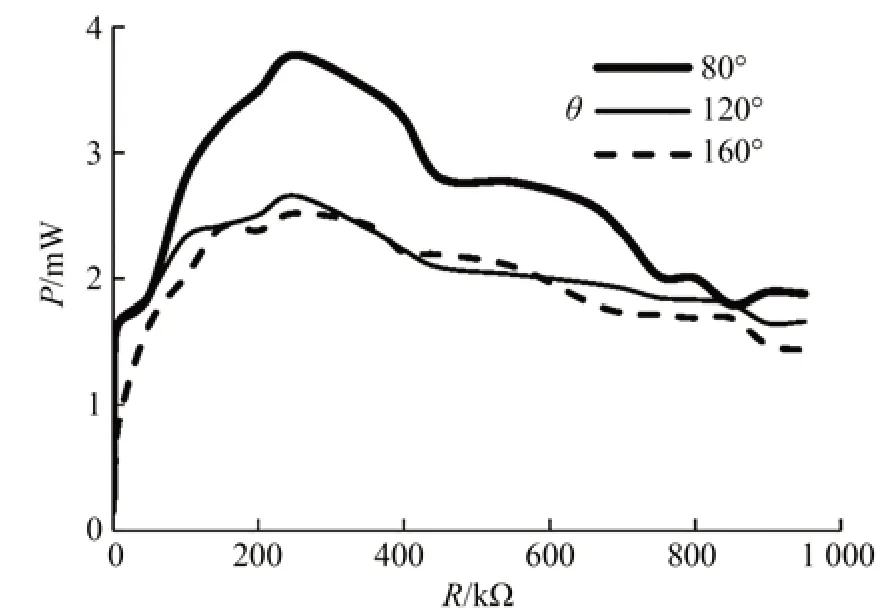
圖13 迎風角θ 不同時輸出功率與負載電阻的關系曲線Fig.13 Relation curve between output power and load resistance when windward angle θ is different

5 結論

為降低起振風速、拓寬工作風速范圍及限制高風速下的系統振幅，本文提出一種可變形式翼型鈍體的風致振壓電俘能器，并通過仿真與試驗研究了不同風速下彈性翼厚和迎風角對俘能器輸出性能的影響規律，獲得如下結論：

（1）俘能器的鈍體由于存在可變形的彈性翼，鈍體的形狀會隨著風速變化而改變，從而使俘能器達到自適應風速調節自身振動特性的目的。當風速較低時，彈性翼形變較小，鈍體呈V字形，其振幅隨風速增大而增大，此時系統以馳振為主；當風速較高但還未超過閾值時，彈性翼形變增大，鈍體呈曲面翼型，其振幅不再隨風速增加而大幅變化，此時系統進入“鎖頻”狀態；當風速超過閾值時，彈性翼變形較大，鈍體呈彎弧狀，其振幅隨風速增加而逐漸減小，此時系統以渦振為主。因此，俘能器鈍體形狀適應風速而變化的特性能夠使得輸出電壓隨風速增大呈先增大后平緩再減小的趨勢；

（2）迎風角和彈性翼厚對鈍體形狀變化及其振動特性的影響較大。在試驗范圍內，當迎風角小于120°時，俘能器在較高風速下會出現失穩現象，從而導致其結構易發生損壞；而當迎風角在120°～180°之間時，俘能器能夠在較高風速下穩定發電，且隨著迎風角的增大，起振風速呈增大趨勢，鎖頻風速呈先減小后增大趨勢，降幅風速和等幅電壓則基本呈減小趨勢。當彈性翼厚大于0.3 mm 時，俘能器由于彈性翼剛度過大產生變形較小，無法改變發散性振動特性而出現失穩現象；但當彈性翼厚不大于0.3 mm 時，俘能器的振動特性會適應風速的變化，且鎖頻風速、等幅電壓及降幅風速均隨彈性翼厚增加而增大；

（3）當選擇較佳的迎風角（120°～160°）、彈性翼厚（0.15～0.3 mm）時，俘能器的起振風速可降至3.24 m/s，穩定工作風速至少可達25 m/s，且存在最佳負載為250 kΩ 時俘能器的最大輸出功率為3.78 mW。