大學(xué)生乒乓球選項課運動技能學(xué)習(xí)評價指標(biāo)模型構(gòu)建

鄒俊峰

(遼寧師范大學(xué) 體育學(xué)院,遼寧 大連 116029)

乒乓球運動易上手,富有競技性、娛樂性和觀賞性,受到大多數(shù)人的喜愛,乒乓球選項課已成為高校體育課中的重要組成部分.我國始終堅持高校體育的改革與發(fā)展,運動技能作為高校體育課程的重要學(xué)習(xí)目標(biāo),構(gòu)建學(xué)習(xí)評價體系尤為關(guān)鍵.目前,我國關(guān)于大學(xué)生乒乓球選項課運動技能學(xué)習(xí)評價的研究多為理論層面,實證性研究較少.傳統(tǒng)的乒乓球選項課運動技能評價方式相對固化、單一,學(xué)生練習(xí)之后在運動技能方面也未得到顯著提升.季瀏認(rèn)為,重視課程內(nèi)容改革和整體設(shè)計,重視運動技能學(xué)練,重視綜合性學(xué)習(xí)評價,倡導(dǎo)評價的激勵、反饋和發(fā)展功能,做到評價內(nèi)容多維,評價方法多樣,評價主體多元[1].因此,構(gòu)建大學(xué)生乒乓球選項課運動技能學(xué)習(xí)評價指標(biāo)模型,不僅為體育教師依據(jù)課程目標(biāo)開展教學(xué)活動和設(shè)計教學(xué)內(nèi)容提供了理論依據(jù)和實踐參考,也為深化課堂改革,提高教學(xué)質(zhì)量以及促進學(xué)生運動技能的發(fā)展提出參考性建議.

1 研究對象與方法

1.1 研究對象

遼寧省、山東省部分高校480名乒乓球選項課學(xué)生

1.2 研究方法

1.2.1 文獻資料法

通過對中國知網(wǎng)(CNKI)的查閱,搜集關(guān)于“乒乓球選項課”“運動技能” “學(xué)習(xí)評價”等方面的文獻資料,了解專家學(xué)者的研究成果以及當(dāng)前領(lǐng)域的研究現(xiàn)狀,為本文指標(biāo)的選取提供借鑒和理論支撐.

1.2.2 德爾菲法

德爾菲法的核心要義是研究者匿名通過可控的數(shù)輪問卷函詢專家[2],并根據(jù)專家的意見與建議對評價指標(biāo)體系完善或優(yōu)化,最終確定大學(xué)生乒乓球選項課運動技能學(xué)習(xí)評價的具體指標(biāo).

1.2.3 數(shù)理統(tǒng)計法

本研究運用 SPSS22.0 統(tǒng)計軟件對所回收的問卷數(shù)據(jù)進行了描述性統(tǒng)計分析、項目分析、信度分析和效度分析(探索性因子分析).運用 AMOS24.0 軟件對問卷回收數(shù)據(jù)進行了效度分析(驗證性因子分析)和模型擬合分析.

2 評價指標(biāo)的確定

2.1 評價指標(biāo)的初擬

Nvivo11是一款強大的質(zhì)性分析軟件,它在扎根理論原理下,經(jīng)過逐層分析,在錯綜復(fù)雜的文本資料中概念化和分類,進行編碼、存儲和提取,通過歸納分析由下位概念到上位概念,最終獲得核心概念與理論.通過查閱文獻和結(jié)合《全國普通高等學(xué)校體育課程教學(xué)指導(dǎo)綱要》形成初始模型.以“乒乓球選項課”“運動技能”“學(xué)習(xí)評價”為關(guān)鍵詞在中國知網(wǎng)、萬方以及外文等數(shù)據(jù)庫進行檢索. 共檢索到2015-2022年有關(guān)文獻52篇,篩選出與大學(xué)生乒乓球選項課運動技能學(xué)習(xí)評價指標(biāo)模型構(gòu)建相關(guān)的文獻27篇.借助Nvivo11軟件對文獻資料編碼,最終建立評價指標(biāo)體系,由大學(xué)生乒乓球選項課運動技能學(xué)習(xí)評價初始模型中的乒乓球基礎(chǔ)知識、乒乓球基本技能與乒乓球安全運動能力3個維度組成.基于《全國普通高等學(xué)校體育課程教學(xué)指導(dǎo)綱要》和文獻研究的結(jié)果,構(gòu)建出大學(xué)生乒乓球選項課運動技能學(xué)習(xí)評價初始模型(見表1).

2.2 指標(biāo)確定

基于問卷的科學(xué)性、系統(tǒng)性和可操作性等原則,本文采用德爾菲法選取15位專家進行3輪問卷調(diào)查,篩選出大學(xué)生乒乓球選項課運動技能學(xué)習(xí)評價指標(biāo).第一、二輪專家建議統(tǒng)計如表2和表3所示.

表2 第一輪專家建議修改的指標(biāo)統(tǒng)計(n=15)Table 2 The first round of experts suggested the revision of the indicator statistics(n=15)

表3 第二輪專家建議修改的指標(biāo)統(tǒng)計(n=15)Table 3 The second round of experts suggested the revision of the indicator statistics(n=15)

在前2輪的調(diào)查中,由于其他指標(biāo)具有較高的贊成度,故不再陳述.有部分專家根據(jù)指標(biāo)的可行性提出修改意見.例如:針對指標(biāo)“C16能夠制定乒乓球競賽規(guī)程”,提出大學(xué)生通過短短一學(xué)期的選項課,無法將自身學(xué)習(xí)的知識體系同制定競賽規(guī)程相結(jié)合,該指標(biāo)在設(shè)計時沒有考慮可行性;指標(biāo)“C24能夠有意識地預(yù)知乒乓球運動危險發(fā)生”與“C25能夠遷移乒乓球安全運動知識”內(nèi)容交叉,建議刪除等.針對15位專家提出的建議修改和完善后,進行第三輪專家調(diào)查問卷,所有指標(biāo)均得到認(rèn)可,最終確定包括3個一級指標(biāo)、6個二級指標(biāo)與23個三級指標(biāo)的評價指標(biāo)體系(初步),如表4所示.

3 評價指標(biāo)體系優(yōu)化

由于德爾菲法帶有一定的主觀色彩,為獲取更加全面、合理的指標(biāo)體系,需對初步確定的大學(xué)生乒乓球選項課運動技能學(xué)習(xí)評價指標(biāo)進行篩選,并優(yōu)化其體系.在上述大學(xué)生乒乓球選項課運動技能學(xué)習(xí)評價指標(biāo)體系的基礎(chǔ)上,形成由23個題項組成的大學(xué)生乒乓球選項課運動技能學(xué)習(xí)初始量表,并形成Likert五級量表形式的調(diào)查問卷,發(fā)放給遼寧省和山東省選修乒乓球課的大學(xué)生.共發(fā)放調(diào)查問卷490份,回收480份,有效問卷450份.對其中240份進行信效度檢驗,在刪除和調(diào)整相應(yīng)的題項后,對另外210份進行結(jié)構(gòu)模型的分析.

3.1 項目分析

對回收的240份問卷進行統(tǒng)計與分析,計算每個樣本全部題項得分,按照總分的前、后27%作為高低分組的指標(biāo),低分組臨界值為80,高分組臨界值為94,以獨立樣本t檢驗檢測各題項的差異.結(jié)果顯示,全部題項在高低分組的平均值差異均達到了顯著性差異水平(p<0.001),且t的絕對值均>3.00的最低標(biāo)準(zhǔn),表明量表各題項具有良好的區(qū)分度,應(yīng)予以保留.

3.2 信度分析

運用SPSS26.0軟件測得CITC值和Cronbach’s α系數(shù),整體 Cronbach’s α 值為0.928且各潛變量的 Cronbach’s α 值均>0.8,一般認(rèn)為當(dāng)CITC<0.5時就應(yīng)該刪除該題項[3].而Q14在修正后的項與總計相關(guān)性(CITC)<0.5,故刪除該題項.在刪除之后,再次測得各題項修正后的項與總計相關(guān)性(CITC)均>0.5.因此,本研究的各題項均達到了較為理想的信度水平,可進行下一步效度檢驗,見表5和表6.

表5 量表信度分析表Table 5 Scale reliability analysis

表6 各維度題項信度檢驗結(jié)果Table 6 Reliability test results of each dimension item

3.3 探索性因子分析

如表7所示,運用SPSS26.0 軟件對所保留的22個觀測變量進行效度檢驗,結(jié)果顯示,其KMO值為0.927>0.7,已達到可接受程度的標(biāo)準(zhǔn)[4].Bartlett’s的球形度檢驗的近似卡方值為4960.214,自由度為231(p=0<0.001) .

表7 KMO和Bartlett的檢驗Table 7 KMO and Bartlett’s test

如表8所示,對觀測指標(biāo)進行探索性因子分析,設(shè)定特征值>1為條件,提取3個主成分因子,分別為大學(xué)生乒乓球選項課運動技能學(xué)習(xí)評價指標(biāo)體系中的3個潛變量,潛變量的解釋總方差統(tǒng)計,其累積的方差貢獻率為77.398%>50%的最低標(biāo)準(zhǔn).如表9所示,對所提取的因子進行旋轉(zhuǎn),得到22個題項的正交因子載荷矩陣且均>0.50,則表明所有題項通過效度檢驗.

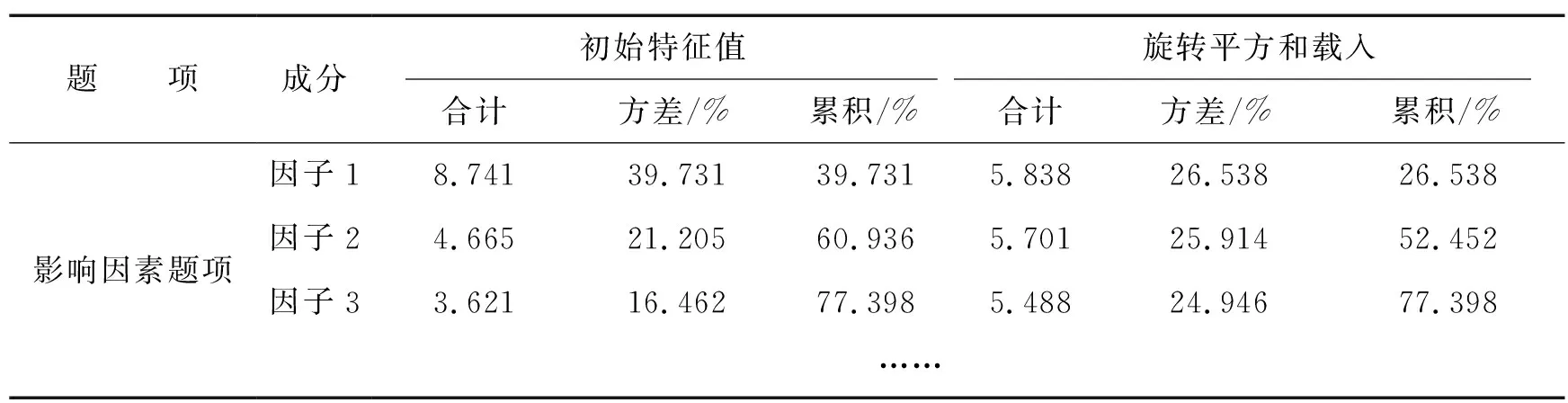
表8 解釋的總方差Table 8 The total variance of the explanation

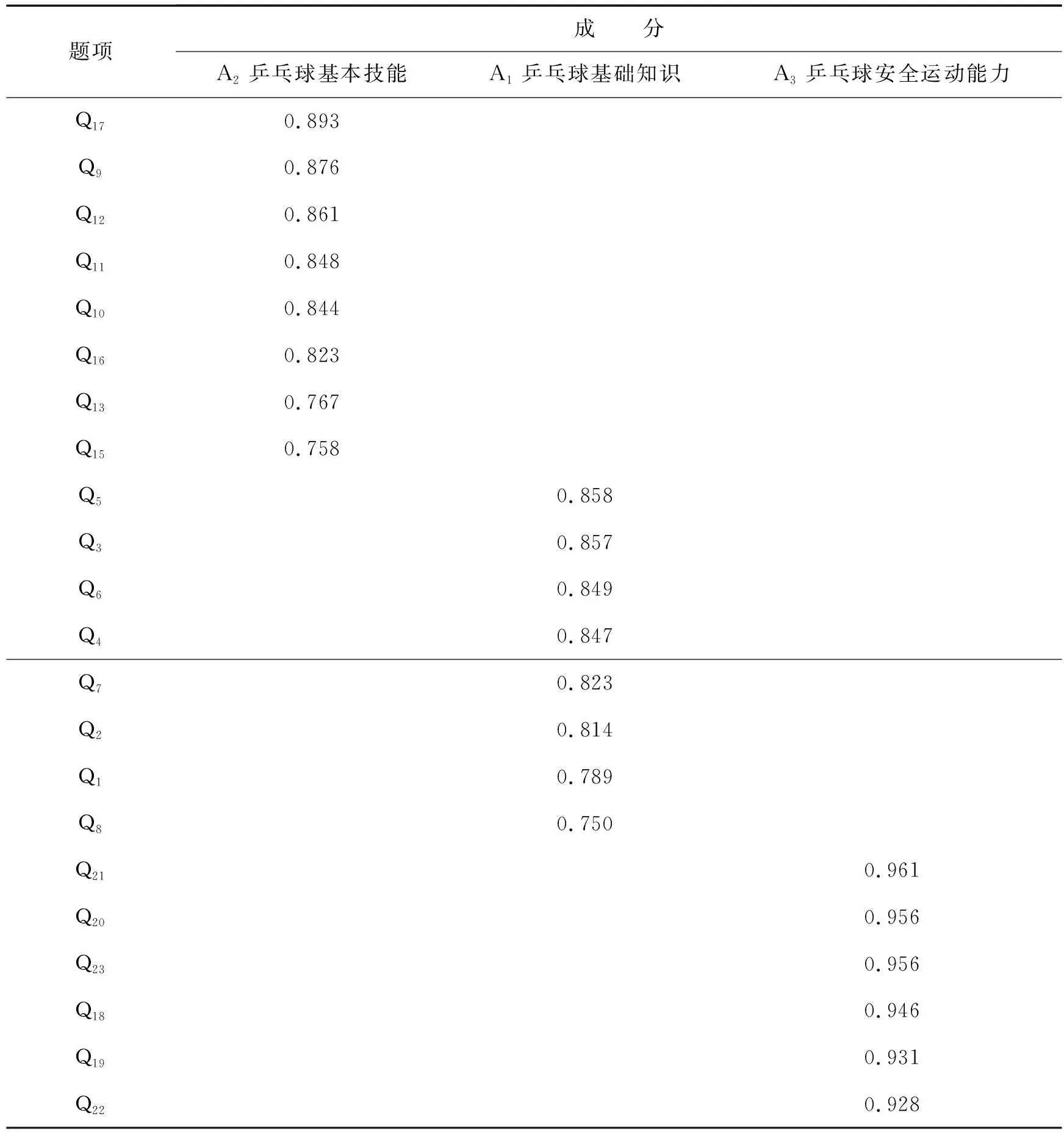
表9 旋轉(zhuǎn)成分矩陣表Table 9 Rotating composition matrix table

綜上所述,經(jīng)過項目分析、信度分析和探索性因子分析對各題項進行檢測,該量表的信度和效度均達到統(tǒng)計學(xué)研究要求,最后得到評價大學(xué)生乒乓球選項課運動技能學(xué)習(xí)的22個觀測指標(biāo).統(tǒng)計結(jié)果可用于下一步的模型分析檢驗.

4 基于SEM的評價模型構(gòu)建

4.1 結(jié)構(gòu)方程模型概述

SEM主要是評估假設(shè)模型,以達到定量研究的目的.這是一種多元統(tǒng)計分析方法,用于檢驗自變量和因變量之間的關(guān)系.通過測量因變量推斷自變量,并驗證假設(shè)模型[5].

4.2 評價模型的假設(shè)

根據(jù)對評價指標(biāo)體系的初選和優(yōu)化,本研究提出運動技能學(xué)習(xí)評價的二階六因子理論假設(shè)模型(圖1):一階為大學(xué)生乒乓球運動技能學(xué)習(xí)評價;二階為掌握乒乓球基本知識,獲取乒乓球知識能力,提高乒乓球技術(shù)水平,增強乒乓球技能運用,乒乓球安全運動行為和乒乓球安全運動認(rèn)知6個因子,分別包括多個觀測指標(biāo).

圖1 大學(xué)生乒乓球運動技能學(xué)習(xí)評價假設(shè)模型Fig.1 A hypothetical model for evaluation of table tennis skill learning of college students

4.3 評價模型識別

結(jié)構(gòu)方程模型在AMOS 24.0中檢驗操作時可能會出現(xiàn)參數(shù)無法估計以及擬合度檢驗不正確的情況.模型識別根據(jù)測量數(shù)據(jù)的高低可劃分為低度識別、正好識別和過度識別.低度識別的模型因為參數(shù)無法估計導(dǎo)致模型無法識別,正好識別是適配度最佳的模型,過度識別的模型是經(jīng)過擬合度檢測后進行修正的模型[6].在模型估計程序中,假設(shè)模型中觀察變量的數(shù)量為p,那么模型識別(df)的計算公式如下:

(1)

其中,t為待估計自由參數(shù),df(Degree of freedom)是測量數(shù)據(jù)數(shù),p是模型中的外因測試指標(biāo)(外衍觀測變量)個數(shù),q是模型中的內(nèi)因測試指標(biāo)(內(nèi)衍觀測變量)個數(shù).若df>0,表示模型過度識別;df=0,表示模型正好識別;若df<0,表示模型低度識別.根據(jù)式(1)計算可知,當(dāng)前假設(shè)模型的數(shù)據(jù)點數(shù)目為253,估計的參數(shù)t共有50個,即研究的假設(shè)模型自由度為二者之差等于203.因此,判定該模型為過度識別,可以進行模型擬合度分析.

4.4 評價模型的擬合

采用AMOS 24.0軟件對假設(shè)模型進行驗證、調(diào)整和修正時,如果數(shù)據(jù)結(jié)果與模型匹配的標(biāo)準(zhǔn)指標(biāo)不匹配,則必須對假設(shè)模型進行調(diào)整和修正,最終獲得與觀測數(shù)據(jù)高度一致的模型.

4.4.1 一階驗證性因子分析

使用AMOS 24.0軟件檢查和分析假設(shè)模型中的變量,以便進行調(diào)整和修正.模型擬合使用ML(最大似然)法,以獲得假設(shè)模型驗證的結(jié)果以及一階模型圖(見圖2).軟件驗證和分析的結(jié)果顯示“OK:Default model”,這意味著該模型能夠順利收斂,一階驗證模型滿足要求.

圖2 一階驗證性因子分析模型圖(標(biāo)準(zhǔn)化解)Fig.2 First-order confirmatory factor analysis model diagram (standardized solution)

4.4.2 一階模型擬合度分析

結(jié)構(gòu)方程模型的優(yōu)劣一般用適配度指數(shù)來反映,主要選取絕對擬合度指標(biāo)和增值擬合度指標(biāo)等,檢測其是否在適配范圍內(nèi).若指標(biāo)數(shù)值均在合理范圍內(nèi)[7],則表示該模型擬合良好;反之,則需根據(jù)修正系數(shù)(MI)對模型進行修正.通過軟件的“ModelFit”,計算模型指標(biāo)真實值和適配指標(biāo),如表10所示.

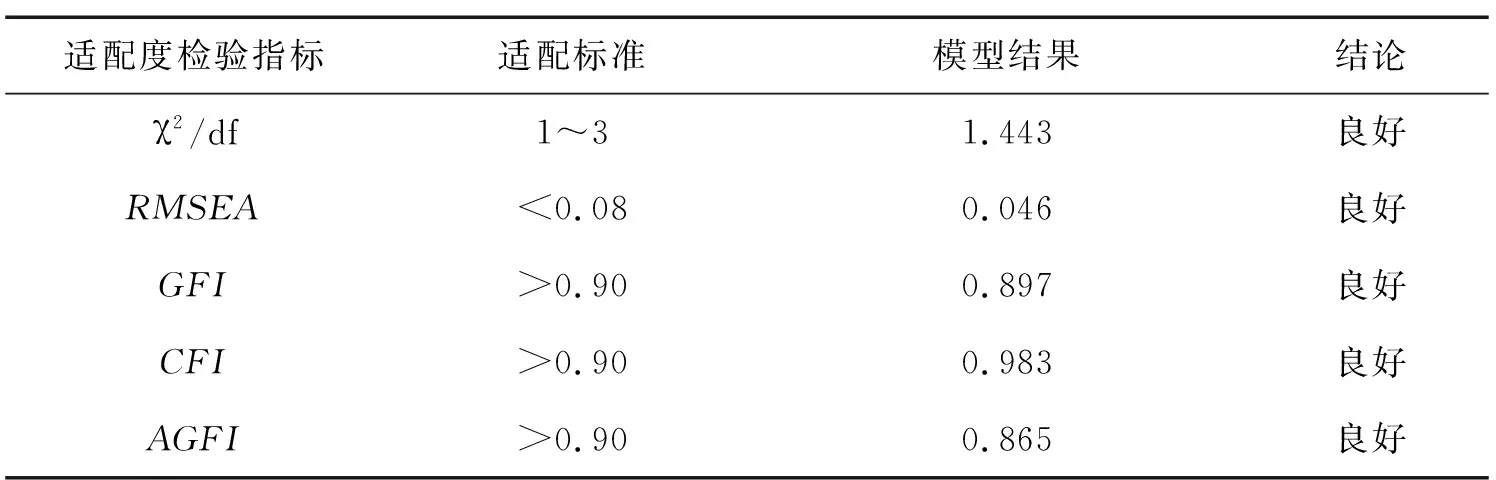
表10 指標(biāo)擬合結(jié)果構(gòu)成表Table 10 Composition table of index fitting results

從表10可知:χ2/df為1.443,符合擬合度<3的標(biāo)準(zhǔn);RMSEA值為0.046<0.08,滿足良好適配標(biāo)準(zhǔn);GFI、AGFI的值不滿足>0.90的標(biāo)準(zhǔn),但是非常接近[8].總體來說,此一階模型可以被接受,因此,需要對模型進一步擬合修正.

4.4.3 二階驗證性因子分析

模型的二階驗證是為了測量更高階因子,其前提是通過模型的一階驗證后方可進行.在CFA模型圖中,運動技能學(xué)習(xí)評價是外因潛變量,其對應(yīng)的6個一階因子成為內(nèi)因潛在變量,因此增加了估計殘差.

根據(jù)模型和擬合度指數(shù)之間的適配情況可以得出假設(shè)模型是否可以接受.通過表11中的二階模型擬合結(jié)果可知,除了AGFI值(0.865<0.90)、GFI的值(0.897<0.90)未達到適配標(biāo)準(zhǔn)外,χ2/df值為504.634/269=1.876,符合<3的標(biāo)準(zhǔn),RMSEA為0.058,符合<0.08的標(biāo)準(zhǔn),均在合理標(biāo)準(zhǔn)區(qū)間內(nèi).

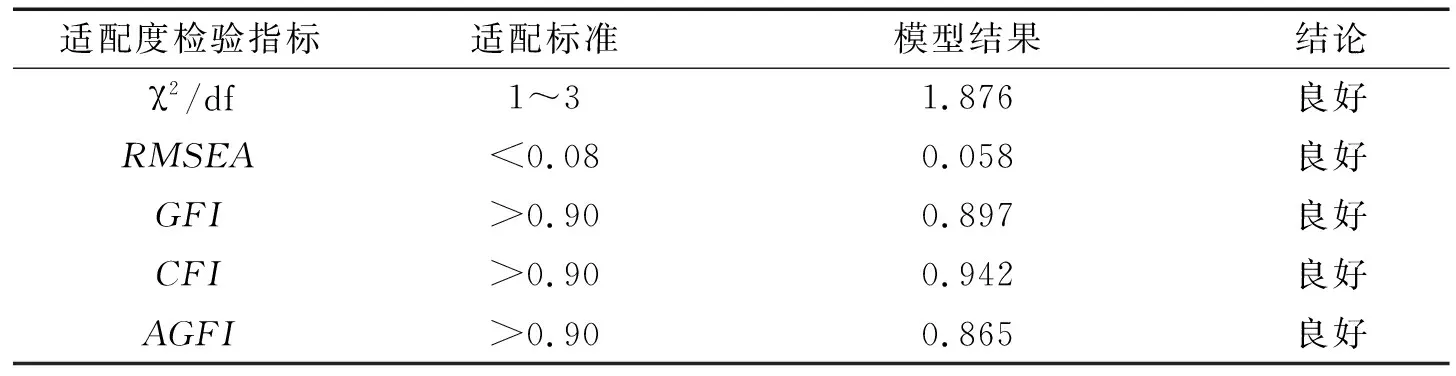
表11 二階模型驗證的擬合指數(shù)Table 11 Fit index for second-order model validation

4.5 MI指數(shù)修正

MI是指把自由度設(shè)定為1時,估計模型前后卡方值之間的差值.根據(jù)修正指數(shù)的大小對模型進行修正,建立相關(guān)觀測變量間的殘差相關(guān)路徑,促進模型適配指標(biāo)值達到標(biāo)準(zhǔn)[9].模型適配值在合理范圍內(nèi)表明模型擬合良好,模型最終設(shè)定.

4.6 修正擬合結(jié)果

根據(jù)修正模型的擬合結(jié)果(表12),χ2/df值為1.375(<2),RMSEA值為0.038(<0.08),其余擬合指數(shù)值均達到標(biāo)準(zhǔn)范圍.基于此可得,修正模型的擬合通過測試達到良好標(biāo)準(zhǔn),模型得到證實.

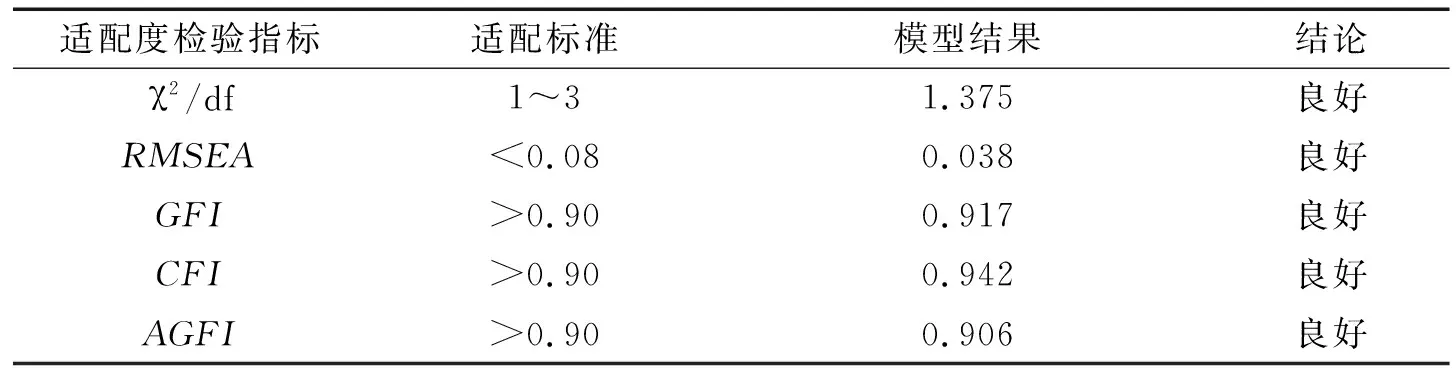
表12 MI修正模型的擬合結(jié)果Table 12 The fitting results of MI correction model

根據(jù)結(jié)構(gòu)方程模型(SEM)中的路徑系數(shù),可以反映出變量之間的關(guān)系.例如:變量之間的值越大,則影響關(guān)系就越大.根據(jù)變量之間的影響關(guān)系,建立相關(guān)的通徑系數(shù)判別標(biāo)準(zhǔn),最后對評價指標(biāo)進行優(yōu)化,建立評價指標(biāo)體系.模型的路徑系數(shù)如表13所示.

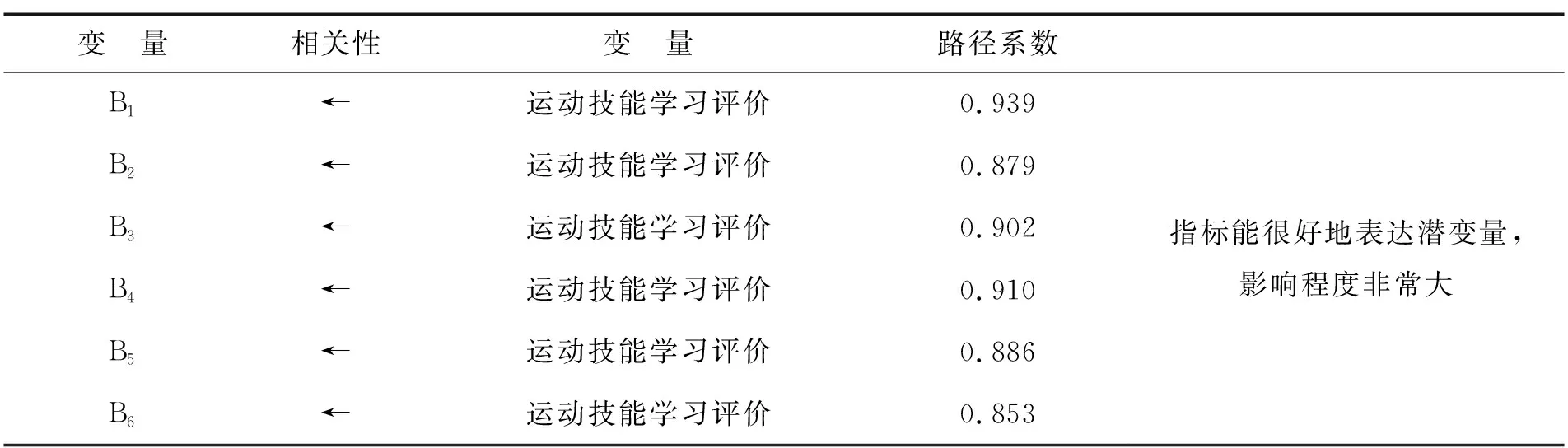
表13 路徑系數(shù)分析表Table 13 Path coefficient analysis table

4.7 權(quán)重分配及評價指標(biāo)體系的確立

本文采用相關(guān)性權(quán)重法計算各個評價指標(biāo)的路徑系數(shù)和權(quán)重值[10].首先,依據(jù)表13計算出各評價指標(biāo)間的路徑系數(shù)和二級指標(biāo)(式2)、三級指標(biāo)(式3)的權(quán)重計算公式,確定評價指標(biāo)權(quán)重系數(shù);其次,對評價指標(biāo)進行驗證和優(yōu)化;最后,根據(jù)結(jié)果確立包含運動技能學(xué)習(xí)評價的一級指標(biāo)、6個維度的二級指標(biāo)、維度相對應(yīng)的22個觀測指標(biāo)(即三級指標(biāo))的初中生乒乓球運動技能學(xué)習(xí)評價指標(biāo)體系(見表14).

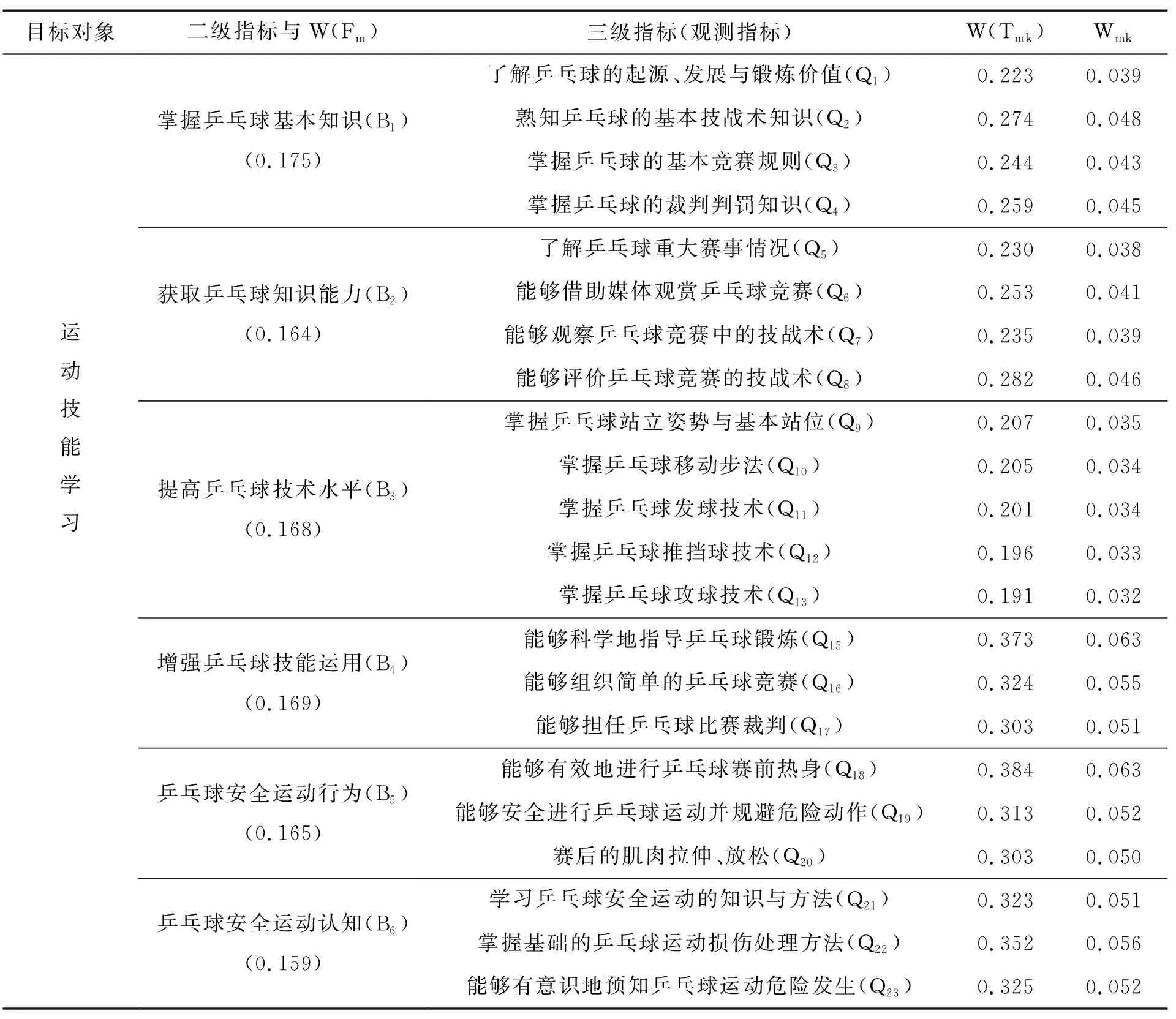
表14 大學(xué)生乒乓球運動技能學(xué)習(xí)評價指標(biāo)體系Table 14 Evaluation index system of table tennis skill learning for college students

(2)

(3)

Wmk=W(Fm)×W(Tmk).

(4)

例如:在式(2)中,計算6個二級指標(biāo)中第一個掌握乒乓球基本知識指標(biāo)的權(quán)重值.首先,從路徑系數(shù)表中可以看出掌握乒乓球基本知識的路徑系數(shù)即R(F1) 為0.939,那么掌握乒乓球基本知識指標(biāo)的權(quán)重值W(F1)為掌握乒乓球基本知識的路徑系數(shù)與6個二級指標(biāo)路徑系數(shù)之和的比值.

即:

W(F1)=0.939/(0.939+0.879+0.902+0.910+0.886+0.853)=0.175.

以此類推,順次計算剩余二級指標(biāo)及三級指標(biāo)的權(quán)重值,最后計算出全部三級指標(biāo)的綜合權(quán)重值,得到大學(xué)生乒乓球運動技能學(xué)習(xí)評價指標(biāo)體系,如表14所示.

4.8 評價指標(biāo)的相關(guān)分析

4.8.1 分析潛在變量之間的路徑關(guān)系

潛在變量相互間路徑系數(shù)可以認(rèn)為是因某一潛在變量的改變導(dǎo)致有關(guān)潛在變量的變化.6個潛變量的權(quán)重占比由大到小分別為17.5%、16.4%、16.8%、16.9%、16.5%、15.9%.由此看出掌握乒乓球基本知識對運動技能學(xué)習(xí)影響最大,其次是增強乒乓球技能運用,提高乒乓球技術(shù)水平,乒乓球安全運動行為,獲取乒乓球知識能力,最后是乒乓球安全運動認(rèn)知.因此,得出某位學(xué)生的運動技能學(xué)習(xí)領(lǐng)域的成績計算公式為:成績=掌握乒乓球基本知識+獲取乒乓球知識能力+提高乒乓球技術(shù)水平+增強乒乓球技能運用+乒乓球安全運動行為+乒乓球安全運動認(rèn)知.成績公式表明運動技能學(xué)習(xí)的提升涉及不同因素的相互協(xié)作,同時各潛變量中任意變量數(shù)值提升都會明顯作用于運動技能成績,變量間不會相互制約、抑制.

4.8.2 路徑分析

在掌握乒乓球基本知識的觀測指標(biāo)中,熟知乒乓球的基本技戰(zhàn)術(shù)知識對運動技能學(xué)習(xí)有重要影響,其路徑系數(shù)、權(quán)重占比、綜合權(quán)重值是0.939、27.4%、0.048.由此說明,在掌握乒乓球基本知識中熟知乒乓球的基本技戰(zhàn)術(shù)知識是提高運動技能學(xué)習(xí)的首要因素;其次是掌握乒乓球的裁判判罰知識,掌握乒乓球的基本競賽規(guī)則和了解乒乓球的起源、發(fā)展與鍛煉價值.

在獲取乒乓球知識能力的觀測指標(biāo)中,能夠評價乒乓球競賽的技戰(zhàn)術(shù)對運動技能學(xué)習(xí)有重要影響,其路徑系數(shù)、權(quán)重占比、綜合權(quán)重值是0.879、28.2%、0.046.由此說明,在獲取乒乓球知識能力中能夠評價乒乓球競賽的技戰(zhàn)術(shù)是提高運動技能學(xué)習(xí)的首要因素;其次是能夠借助媒體觀賞乒乓球競賽,能夠觀察乒乓球競賽中的技戰(zhàn)術(shù)和了解乒乓球重大賽事情況.

在提高乒乓球技術(shù)水平的觀測指標(biāo)中,掌握乒乓球站立姿勢與基本站位對運動技能學(xué)習(xí)有重要影響,其路徑系數(shù)、權(quán)重占比、綜合權(quán)重值是0.902、20.7%、0.035.由此說明,在提高乒乓球技術(shù)水平中掌握乒乓球站立姿勢與基本站位是提高運動技能學(xué)習(xí)的首要因素;其次是掌握乒乓球移動步法,掌握乒乓球發(fā)球技術(shù),掌握乒乓球推擋球技術(shù)和掌握乒乓球攻球技術(shù).

在增強乒乓球技能運用的觀測指標(biāo)中,能夠科學(xué)地指導(dǎo)乒乓球鍛煉對運動技能學(xué)習(xí)有重要影響,其路徑系數(shù)、權(quán)重占比、綜合權(quán)重值是0.910、37.3%、0.063.由此說明,在增強乒乓球技能運用中,能夠科學(xué)地指導(dǎo)乒乓球鍛煉是提高運動技能學(xué)習(xí)的首要因素;其次是能夠組織簡單的乒乓球競賽和能夠擔(dān)任乒乓球比賽裁判.

在乒乓球安全運動行為的觀測指標(biāo)中,能夠有效地進行乒乓球賽前熱身對運動技能學(xué)習(xí)有重要影響,其路徑系數(shù)、權(quán)重占比、綜合權(quán)重值是0.886、38.4%、0.063.由此說明,在乒乓球安全運動行為中,能夠有效地進行乒乓球賽前熱身是提高運動技能學(xué)習(xí)的首要因素;其次是能夠安全進行乒乓球運動并規(guī)避危險動作和賽后的肌肉拉伸、放松.

在乒乓球安全運動認(rèn)知的觀測指標(biāo)中,掌握基礎(chǔ)的乒乓球運動損傷處理方法對運動技能學(xué)習(xí)有重要影響,其路徑系數(shù)、權(quán)重占比、綜合權(quán)重值是0.853、35.2%、0.056.由此說明,在乒乓球安全運動認(rèn)知中,掌握基礎(chǔ)的乒乓球運動損傷處理方法是提高運動技能學(xué)習(xí)的首要因素;其次是能夠有意識地預(yù)知乒乓球運動危險發(fā)生和學(xué)習(xí)乒乓球安全運動的知識與方法.

5 結(jié) 論

本文以大學(xué)生乒乓球選項課運動技能學(xué)習(xí)評價為切入點,對影響該技能成績的6個潛變量進行權(quán)重比檢驗,并得出預(yù)期結(jié)果證實該模型構(gòu)建的合理性、科學(xué)性,為大學(xué)生乒乓球選項課運動技能學(xué)習(xí)評價指標(biāo)體系的構(gòu)建提供了一定的理論依據(jù)和實踐參考.