介觀統計熱力學理論與實驗*

全海濤 董輝 孫昌璞1)?

1)(北京大學物理學院,北京 100871)

2)(中國工程物理研究院研究生院,北京 100193)

1 引言

眾所周知,傳統熱力學和統計物理是關于宏觀系統(通常包含 1023個以上粒子)的理論.然而,當系統有限、偏離熱力學極限時,傳統的熱力學和統計物理理論是否依然成立? 量子效應是否影響系統的熱力學性質? 或者統計物理和熱力學理論需要做哪些修改或補充? 學界對這些基本問題并沒有進行充分的研究,對許多困惑也沒有形成共識.在過去的近20年里,隨著介觀物理、納米技術和量子信息領域的不斷發展,統計熱力學的研究經常面臨只包含少數粒子,甚至只有幾個粒子的體系的挑戰.在這種遠遠偏離熱力學極限的系統,原本適用于宏觀系統的熱力學和統計物理理論是否依然成立,這已經成為亟待解決的基礎科學問題,并且在許多實際應用中具有迫切的需求(如核電池的循環和人工光合作用等領域).當考慮到極低溫情況時,量子效應也不能被忽略.因此,對于介觀的小系統,比如Szilard 單分子熱機,人們必須重新審視熱力學和統計物理理論.特別對于不能忽略量子效應的小系統,統計熱力學研究已經成為近20年來的研究熱點之一.在過去的近20年里,我們在介觀小系統的統計熱力學及其應用方面開展了一系列的研究,這些研究在國際學術界引起了較大的反響,實質性地推動了這一新興領域的發展.本文將對該領域的發展,以及我們相關的工作和未來展望方面進行簡要介紹.

對于小系統,我們用粒子數和過程時間兩個尺度刻畫其介觀特性.一方面,研究對象從宏觀到介觀和微觀,伴隨著所研究的物理系統的粒子數或尺寸變小,熱漲落和量子漲落變得至關重要,這導致了如小系統非平衡統計物理或者納米熱力學等新興學科方向的產生,特別是小系統中量子相干性和熱庫-系統量子糾纏推動了關于統計物理基礎理論的前沿研究;另一方面,我們所研究的物理系統的動力學過程時間尺度變短,體系偏離平衡態,這催生出了有限時間熱力學等研究方向.其中,動力學控制對熱力學過程影響也已成為近些年的熱點研究方向.圖1 總結了統計熱力學向介觀小系統發展的這一新趨勢和前沿方向.

圖1 統計熱力學發展“新相圖”Fig.1.New diagram for the development of statistical thermodynamics.

本綜述是在筆者及合作者們多年在介觀統計熱力學領域的研究基礎上的總結,同時也反映了國際上熱力學發展的趨勢: 在空間尺度上從宏觀尺度走向介觀微觀量子的尺度;在時間尺度上從平衡態走向有限時間的非平衡過程.需要指出的是,受自身學識的局限和偏好的影響,本文并未試圖、也不可能對整個領域進行全面的、或者包羅萬象的介紹,只選擇了筆者比較熟悉的方面進行闡述.希望能為相關研究者提供一些有價值的參考和借鑒.

2 量子熱機與Maxwell 妖

近20年來,受到量子信息發展的帶動以及實驗技術進步的影響,量子力學和統計物理學的一些基本問題重新受到物理學家的關注.量子熱機(見圖2)為研究這些問題提供了一個很好的平臺.顧名思義,量子熱機[1–3]是以“量子物質”為工作物質并且把吸熱轉化為對外做功的機器.由于工作物質的量子屬性,量子熱機具有很多不同于經典熱機的非凡特質.量子熱機工作物質的量子性成為一個備受關注的新研究熱點[4].人們試圖通過實驗發現一些有別于傳統熱力學理論的新現象和新效應.在理論研究方面,一些超越人們傳統觀念的新奇結論陸續被發現.比如,在一定條件下,量子熱機在每個循環過程中的對外做功量可以超過對應的經典熱機[5,6],而且量子熱機的效率似乎可以超越經典熱機的效率上限——經典Carnot 熱機的效率[7].量子熱機不僅有助于研究量子力學和熱力學的關系,還有助于理解量子測量和量子退相干問題.此外,它還能很好地體現量子和經典熱力學系統的差異,幫助我們理解熱力學過程中的量子-經典過渡的問題[8].

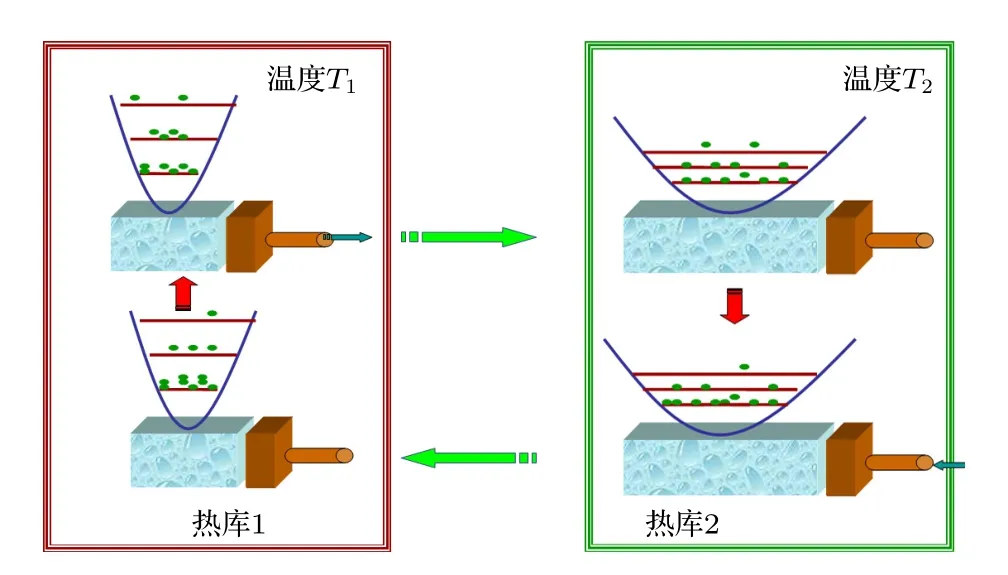
圖2 一個基于離散能級系統的量子熱力學循環Fig.2.A quantum thermodynamic cycle based on a discrete system.

然而,在2007年之前,關于單量子系統的熱力學研究比較缺乏,有關量子熱力學過程和量子熱力學循環的概念較為混亂.考慮到這一狀況,2007年,筆者及合作者[9]系統地研究了量子系統的熱力學過程和熱力學循環,澄清了包括量子等溫過程,量子等容過程,量子Carnot 循環,以及量子Otto循環等量子熱力學的基本概念.這方面的相關工作在量子熱力學領域產生了較大的國際影響.下文將簡述筆者團隊在這一領域的研究成果,其中主要包括將做功、傳熱、等溫過程、Carnot 熱機、Otto 熱機等概念推廣到小量子系統.

2.1 量子熱機研究

平衡態統計熱力學建立于經典力學基礎之上.然而,微觀粒子遵循更基本的量子力學規律,而經典力學只是量子力學的經典近似.因此,如何將統計熱力學理論推廣到量子系統,尤其是只有少數自由度的小量子系統,是一個值得研究的問題.比如,如何把“做功”和“傳熱”等經典熱力學概念推廣到單量子系統,如何在單量子系統中表述熱力學第一定律,另外還有一些與此關聯的問題,如何描述有限時間內的熱力學過程(即非準靜態或非平衡態過程),以及如何刻畫小尺度(非熱力學極限)系統的熱力學性質.這些都是長期以來一直被忽視,但又十分重要的問題.由此已經催生出一個專門的領域,被稱為量子熱力學[10].下面我們就以具有離散能級的單量子系統為例,將經典熱力學的一些概念做量子推廣,并介紹一些量子熱力學的基本概念,以及我們在本領域的一些工作.首先介紹如何在單量子系統表述“做功”和“傳熱”.

考慮一個任意多能級單量子系統(見圖3).為了簡單起見,考慮的系統只包含離散能級結構,并且只含有有限個本征能級.當然,也可以更一般地考慮具有無窮多個能級的系統.

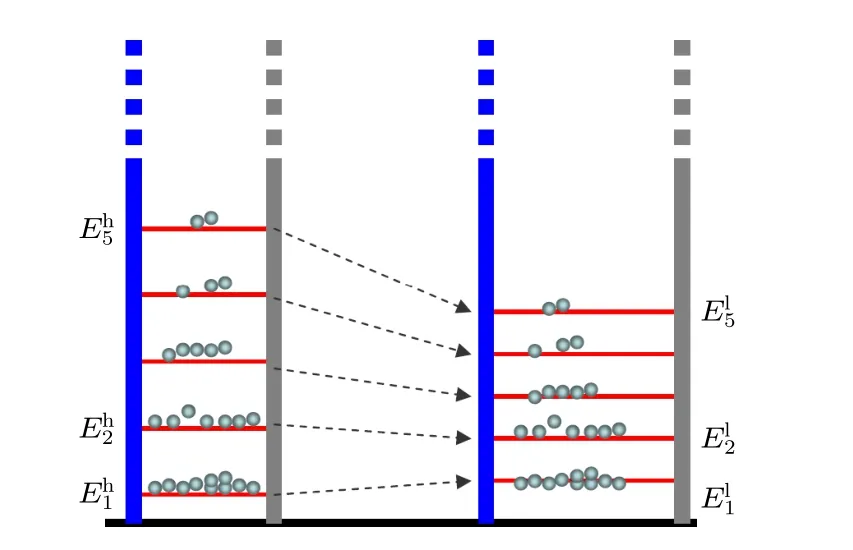
圖3 作為量子熱機工作物質的多能級量子系統,這里展示一個量子絕熱過程Fig.3.A quantum system with discrete energy levels as the working substance,here a quantum adiabatic process is illustrated.

該單量子系統的哈密爾頓量可以寫成:

式中 |n〉是系統的第n個本征態,En是其第n個本征能量.對于這個系統,如果已知其在各個能級上的布居數Pn,那么其內能U可以表示為

為了將一些基本的熱力學過程推廣到單量子系統,也就是定義單量子系統的等溫過程和等容過程,需要先找到傳熱 δQ和做功 δW在單量子系統的表述.從方程(2)可以得到:

在經典熱力學中,熱力學第一定律被表述為

其中 δQ=TdS,[11];T和S分別是溫度和熵;yi是廣義坐標,Yi是與yi共軛的廣義力.考慮到von Neumann 熵S和各個本征能級En上的布居數Pn的關系(kB是Boltzmann 常數):

可以定義單量子系統的熱傳遞和做功[12–14]如下:

方程(6)意味著“做功”相應于本征能級En的改變.這一點與另一個常識性的結論一致,即做功必然伴隨著系統的廣義坐標的改變.而在單量子系統中,廣義坐標的改變又導致了系統本征能量的改變.因此,通過方程(6)和(7)關于做功和熱傳遞在單量子系統的表述,熱力學第一定律在單量子系統的表述 dU=δQ+δW就可以從方程(4)得到.需要強調的是,基于方程(6)和方程(7)關于做功和傳熱的定義,可以建立一套自洽的統計熱力學理論.在這個理論體系里面,壓強p和體積V不再是基本的,也不再是必需的參數.而{En}和{Pn}才是建立統計熱力學理論所必需的元素.可以在某些無法定義壓強和體積的系統,比如一個諧振子或者一個二能級系統利用方程(6)和方程(7)建立自洽的統計熱力學理論.當然,對于可以明確定義壓強和體積的系統,比如活塞中的氣體,方程(6)和方程(7)給出的做功和傳熱的定義與δQ=TdS,δW=-pdV一致.由此可見方程(6)和方程(7)是更一般的、比 δQ=TdS,δW=-pdV適用范圍更廣的關于做功和傳熱的定義.此外,還需要強調,經典系統的熱傳遞表達式δQ=TdS,僅僅適用于準靜態過程.與之一致的是,量子系統的做功和傳熱的方程(6)和方程(7)也只適用于準靜態過程.在2007年之前的文獻[7,15] 中,關于量子熱機(比如量子Carnot 熱機和量子Otto 熱機)的定義并不一致,有的甚至互相矛盾.因此量子Carnot 熱機和量子Otto 熱機的性質難以清晰闡明.這種情況促使我們為各種量子熱機循環提出普適的定義.任何一個量子熱機的循環都是由若干基本的量子熱力學過程組成的.有了單量子系統做功和傳熱的定義,就可以研究單量子系統的熱機循環.下文將描述(由這些量子熱力學過程構成的)平衡態熱力學循環的性質,同時將量子熱機的性質與經典熱機的性質進行比較.

經典Carnot 熱機是一種非常典型的熱機,其每個循環的4 個沖程的熱力學性質都非常清晰,而且它代表了一類普適的可逆熱機的物理機制.目前,關于量子熱機的研究大多集中在對經典Carnot熱機的量子力學推廣方面,也就是對量子Carnot熱機有關方面的研究.

量子Carnot 熱機(一個基于二能級系統的量子Carnot 熱機循環的示意圖見圖4),如同與其對應的經典Carnot 熱機一樣,由兩個(量子)等溫過程 A→B 及 C→D 和兩個(量子)絕熱過程B→C及 D→A 構成.在等溫膨脹過程 A→B 中,工作物質,即被束縛在勢阱中的一個粒子始終與一個溫度為Th的熱源相接觸.工作物質的能級改變的速度比系統的弛豫速度慢得多,以至于這個粒子一直與熱庫保持在熱平衡狀態.

圖4 一個基于二能級量子系統的量子Carnot 熱機循環,Th和 Tl分別代表高溫和低溫熱庫的溫度,?和Pe代表二能級系統的能級差和激發態上的布居數,P和V 代表經典理想氣體的壓強和體積Fig.4.A quantum Carnot cycle based on a two-level system,Th and Tl denote the temperatures of two reservoirs,? and Pe denote the level spacing and the probability in the excited state,P and V denote the pressure and the volume of the ideal gas.

要使量子熱機對外做正功,熱機的兩個熱庫必須滿足條件Th>Tl.這個對量子Carnot 熱機的限制也就是所謂的量子Carnot 熱機的“正功條件”,和經典Carnot 熱機的“正功條件”是一樣的.此外,為了說明定義的量子Carnot 熱機是經典Carnot熱機的量子力學對應,在圖4(c),(d)中給出了量子和經典Carnot 熱機循環的溫度-熵循環(T-S)圖.從圖中可以看到,經典和量子的Carnot 循環的T-S圖具有完全相同的形式.基于上述理由,可推斷本文給出的量子Carnot 熱機循環是經典Carnot 熱機循環的量子力學對應.

量子Otto 熱機循環是另一類很重要的量子熱機循環,其也引起了很多關注.與Carnot 循環類似,經典Otto 循環的量子力學對應也有很多研究[9].實際上,汽車的內燃機所進行的循環就是經典Otto 循環(而非經典Carnot 循環).Otto 循環由兩個經典的等容過程和兩個經典的絕熱過程構成.量子Otto 循環由兩個量子等容過程和兩個量子絕熱過程組成.需要指出的是,文獻[1] 中提到的第1 個量子熱機模型事實上是一個量子Otto熱機模型.因為它的熱機效率和正功條件分別是1-?1/?0和Th>(?0/?1)Tl,其中?1及?0分別是工作物質的兩個能級差,Th和Tl分別是兩個熱庫的溫度.

從研究結果可以看出,盡管量子屬性會帶來一些有別于經典的特征,但是基于單量子系統的量子熱機的性能并沒有超越經典熱機.而在量子信息領域,量子信息處理相比于經典信息處理具有顯著的優勢,兩者形成了鮮明的對比.

2.2 Maxwell 妖與信息“制冷機”

1860年左右,Clausius 和Kelvin 獨立提出了熱力學第二定律.之后不少物理學家曾一度對其普適性持有懷疑態度.一些研究者提出各種“反例”,試圖說明熱力學第二定律可能違反概率性.其中一個重要的例子是物理學家Maxwell 在1871年提出來的一個思想實驗.后來這個思想實驗中的假想智慧生命被開爾文命名為Maxwell 妖,并且引起了很多物理學家的興趣.多位物理學家前赴后繼投入大量精力去研究這個思想實驗,以及其與熱力學第二定律可能矛盾的方面[16].對Maxwell 妖的研究持續了一百多年.直到1982年,這個困擾物理學界一個多世紀的難題才最終被物理學家Bennett利用Landauer 原理(Landauer 在研究計算能耗時提出的)解決.下文將簡述這段熱力學發展史上著名的思想實驗,并介紹我們在這個領域的一些工作.

Maxwell 妖是一種能夠區分單個氣體分子速度的假想物(見圖5(i)),它能夠讓一個容器內運動快(“熱”)的分子和運動慢(“冷”)的分子分別占據不同的區域,從而使容器中不同區域的溫度不同[16].這個結論似乎與熱力學第二定律相違背: 當把高溫和低溫分子集合當成兩個熱源,在它們之間放置的熱機,能夠利用溫差對外做功.整體來看,Maxwell妖的引進,使得“從單一熱源吸熱完全轉化為對外做功”成為可能,從而出現了違反熱力學第二定律的第二類永動機.這就是“Maxwell 妖佯謬”.在相當長的時間內,物理學家們沒有能夠對“Maxwell 妖佯謬”給出一個很滿意的解釋.這個問題的一個重要的進展是1929年物理學家Szilard[17]引入的單分子熱機模型(見圖5(ii)).在這個簡化了 的Maxwell妖熱機模型中,Szilard 首次將信息的概念引入到熱力學循環中.他直觀地認為,Maxwell 妖測量分子處于左邊還是右邊是一個獲取信息的過程,可能會消耗能量,從而導致整體的熵增大.如果把這個消耗包含到熱力學循環中來,就不違反熱力學第二定律,Maxwell 妖佯謬也就迎刃而解.

圖5 Maxwell 妖和Szilard 單分子熱機模型Fig.5.Maxwell’s demon and Szilard single-molecule heat engine model.

可是Szilard[17]的解釋并沒有被最終接受,在隨后的幾十年內,對這個問題的爭論一直沒有停止.直到1961年,有關Maxwell 妖佯謬的研究有了一個革命性的突破.在研究計算過程的熱力學本質時,物理學家 Landauer[18]發現了一個著名定理:每擦除1 bit 的信息將會導致kBTln2—10-21J 熱量的耗散.這就是本文所述的Landauer 原理,其將信息理論和物理學的基本問題聯系在一起.這個原理提出后不久,Landauer 的同事Bennett[19]意識到信息擦除與Maxwell 妖佯謬問題有極其密切的關系,并在1982年利用Landauer 原理從原理上解決了Maxwell 妖佯謬[16].Landauer 原理的實驗驗證由Bérut 等[20]于2012年完成.過去15年左右,產生了一個與Maxwell 妖相關的前沿研究領域——信息熱力學[21],其是Maxwell 妖相關研究與隨機熱力學相結合的產物.

2006年,筆者和合作者研究了如何利用超導量子比特實現包含Maxwell 妖的熱力學循環[22,9,23],研究動機是如果在量子領域存在Maxwell 妖,是否會從本質上改善量子熱機的效率? 研究中量子測量被處理成一個產生系統和測量儀器之間的理想量子糾纏的相互作用動力學過程,避免了使用在基本觀念上備受爭議的波包塌縮假設.因此,從根本上改進了原來的包含Maxwell 妖的量子熱機模型,讓一個充當熱機介質的二能級系統 S 首先與溫度為TS的熱庫接觸,而另一個充當Maxwell 妖的二能級系統 D 被置于溫度為TD的熱庫當中.開始時二者均處于熱平衡態,然后脫離熱庫.用 D 測量S所處的態,并根據測量結果對 S 進行反饋控制(采用可控的CNOT 門),如果 S 處在激發態上,D就將其翻轉到基態上;如果 S 處在基態上,D 就讓其保持不變.最后讓它們分別與各自的熱庫充分接觸,在達到熱平衡態后,完成一個熱力學循環.計算表明,這樣熱機的效率形式上為η=1-??D/?S,其中?D和?S是兩個二能級系統的能級差.?是一個與D 和S 初始分布有關的物理量.通過分析發現在特定的條件下,比如TD足夠低時,這個熱機等價于一般的量子Otto 熱機.詳情見文獻[22].總體而言,包含Maxwell 妖的熱機沒有違背熱力學第二定律的現象.另外,我們還提出了基于超導量子電路的Maxwell 妖量子熱機的物理實現及其量子操控方案.

作為Maxwell 佯謬的一個重要模型,Szilard單粒子熱機引入信息控制的概念,突顯了信息在有限系統熱力學中的作用.當時熱力學中的一個重要問題是如何體現Maxwell 妖在參與量子熱機的熱力學循環中的具體作用.我們構造了一個全量子的Szilard 單粒子熱力學循環[24]: 熱機主要是由束縛在一維無限深勢阱中的單粒子以及一個可以移動的壁構成,Maxwell 妖則是由一個二能級系統構成.讓Maxwell 妖處在與熱機不同的溫度上,實際上我們構造了一個在不同溫度之間工作的熱機.在這種有Maxwell 妖輔助的系統中,量子相干性確實有助于提高熱力學循環的工作效率.通過證明熱機的工作效率低于理想的Carnot 熱機,說明Maxwell 妖的存在實際上并不會破壞熱力學第二定律.基于類似的循環,在全同多粒子體系的Szilard 循環中也得出了同樣的結論[25],并發現全同統計性質對循環效率的影響.

1982年Bennett[19]的開創性工作雖然說明Maxwell 妖不會對熱力學第二定律構成威脅,即擦除其存儲單元的信息,保證熱力學第二定律不會被違反,但是他的假想實驗似乎仍然沒有完全擺脫“智慧精靈”這個假設.有“智慧精靈”參與的(非自動化的)信息熱機模型不可能在實驗室實現,因為世界上不存在這樣的“智慧精靈”.那么,是否有可能設計一個完全自動化的Maxwell 熱機或Maxwell 制冷機? 即沒有任何“智慧精靈”的參與,這個機器能夠實現Maxwell 最初的設想,并且得到和Landauer 原理預言相一致的結果.如果能夠構造出一個自動化的信息熱機模型,將有希望在實驗室中真正制造出一個信息熱機或信息擦除器,從而實現Maxwell 最初的設想.這個裝置不僅可以幫助理解信息、熵、熱、功這些物理學基本概念,還具有很重要的應用前景.2013年Mandal 等[26]考慮了一個自動化的信息制冷機模型.與信息熱機類似,這個自動化的模型通過消費輸入的存儲單元利用熱漲落將熱量從低溫熱庫輸送到高溫熱庫,或者相反通過消費高溫熱庫的熱量,實現對存儲單元上信息的(部分)擦除.這個模型真正體現了Maxwell在1871年提出的思想實驗的內涵.有關這個模型的更詳細的情況請參閱文獻[26].

3 隨機熱力學與漲落定理

當系統偏離熱力學極限時,小系統的熱力學量的平均值不足以描述系統的全部行為,此時漲落變得至關重要.事實上,熱力學量的漲落蘊含了豐富的非平衡過程的信息,對熱力學量漲落的研究深化了對熱力學第二定律的理解.1961年Feynman 提出一個思想實驗,即Feynman 棘輪的裝置(見圖6).如果只考慮熱力學量的平均行為,而不考慮漲落,就無法理解Feynman 棘輪的工作原理.考察這一系統的能量轉化時,傳統功和熱的定義已然失效.1997年,Sekimoto[27]在研究Feynman 棘輪系統時首次將功和熱定義在了單條隨機軌道之上(幾乎在同時,Jarzynski[28]獨立引入了軌道功的概念,與Sekimoto 引入的軌道功定義一致),直接催生了隨機熱力學這個領域.

圖6 Feynman 棘輪,TA和TB代表兩個熱庫的溫度,有關Feynman 棘輪的介紹可參考文獻[27]Fig.6.Feynman’s ratchet.TA and TB denote the temperatures of two reservoirs.For an introduction to Feynman’s ratchet please refer to Ref.[27].

隨機熱力學在隨機軌道意義上定義熱力學量并重新表述熱力學第一定律和第二定律.下面我們用一個具體的例子闡釋隨機熱力學的主要定義和內容.考慮這樣一個過程,系統與溫度為T的熱庫接觸,系統受一個隨時間改變的外部參量λ(t)控制,比如活塞系統的長度、諧振子系統的頻率等等.λ(t)改變的同時便是外部對系統做功,所以λ(t)也被稱為功參量[29].初始時刻t=0 時系統處于一個態,t=τ為終止時刻,系統處于另一狀態,只要λ(t)改變得不是無窮緩慢(即準靜態過程),那么過程中每一時刻(包括末態)都是非平衡態,整個過程便是非平衡過程.以一維膠體粒子系統為例,粒子滿足朗之萬方程:

(8)式是描述布朗粒子在相空間(x,v)的隨機軌道隨時間t的演化方程,其中x為位置,v為速度.(8)式中m為粒子的質量,γ為Stokes 黏滯系數,β=kBT-1為溫度倒數,F(x,t)代 表勢場力F(x,t)=-?U(x,λ(t))/?x,其中U(x,λ(t))代表勢場.(8)式中速度方程的最后一項代表隨機力,其中ξ(t)是歸一化的白噪聲,滿足〈ξ(t)〉=0,〈ξ(t)ξ(t′)〉=δ (t-t′),其中尖括號代表平均的含義.

系統的哈密頓量為

其中z=(x,v)為相空間坐標.

不同于傳統熱力學,微觀系統中的做功和傳熱需要重新定義,它們都是隨機軌道 [z(t)] 的泛函.1997年,軌道功W和軌道熱Q的定義由物理學家Jarzynski[28,30]和Sekimoto[27,31]分別獨立給出(這里指外界對系統所做的功W和系統從外界吸的熱Q):

由朗之萬方程(8)可知,軌道熱是阻尼力和隨機力的貢獻,正好可以表示成系統哈密頓量因為相空間坐標的改變而產生變化;那么剩余部分,即系統哈密頓量因為功參量λ(t)的改變而產生變化,便被定義為功.這樣的定義保證了熱力學第一定律,即能量守恒:

有了功、熱和熵產生的定義,熱力學第二定律也可以被重新表述.在小系統中,由于有漲落的存在,熱力學第二定律將只會在統計平均的意義上成立[29,32]:

其中 ?F為過程前后系統的自由能差.(11)式 和(12)式的具體證明會在下一節漲落定理中給出.

除了以上軌道功、熱、熵產生的定義之外,隨機熱力學中引入的其他熱力學量還包括更加細致的 housekeeping 熱、excess 熱[33,34]、環流[32,35,36]等概念.這些是近些年Esposito 等[37–39]工作的基礎.

3.1 經典漲落定理

對于小系統的非平衡過程,物理學家從1993年開始陸續發現了很多對于任意原理平衡過程都嚴格成立的恒等式,統稱為漲落定理.而熱力學第二定律作為推論從漲落定理導出.漲落定理有很多,其中最著名的結果便是 Jarzynski 恒等式,由Jarzynski[28,30]于 1997年提出:

Jarzynski 恒等式成立的條件是初態為熱平衡態.對 Jarzynski 恒等式利用一次Jensen 不等式〈ex〉 ≥e〈x〉,便很容易得到(12)式,即熱力學第二定律.另外可以看到在小系統熱力學第二定律會有一定的概率被“違反”.其概率由公式P[W

理論上,Jarzynski 恒等式可以經由多種途徑推導出來[30].另外,它的正確性和普適性(任意系統、任意溫度、任意速度)通過了很多數值模擬研究的檢驗和實驗驗證[30].作為最早被發現和至今僅有的幾個描述任意遠離平衡過程的熱力學恒等式(另外還有Crooks 漲落定理[43]等)之一,它為研究遠離平衡過程的熱力學打開了一扇窗.

Jarzynski 恒等式的發現是熱力學研究歷史上的一座里程碑.它首次建立了遠離平衡過程的恒等式.在那之后研究人員陸續發現了一些比Jarzynski恒等式更加細致的漲落定理,比如Crooks 漲落定理[43]、Hummer-Szabo 漲落定理[44]和微分漲落定理[45,46].這些漲落定理構成了一個“家族”.文獻[47]整理了這些漲落定理之間的邏輯關系,參見圖7.

圖7 漲落定理家族,這些漲落定理并不互相等價,箭頭代表“可以推導出”,詳情見文獻[47]Fig.7.Hierarchy of fluctuation theorems,these fluctuation theorems are not equivalent to each other.The arrows indicate“can lead to”.Details see Ref.[47].

不難看出“微分漲落定理”在整個領域占據著特別重要的地位.其他漲落定理都可以從這個最基本的漲落定理推導出來.雖然Jarzynski 恒等式等粗粒化的漲落定理早在2002—2005年前后就已經在多種實驗系統中(比如單個RNA 分子鏈和水溶液中的膠體粒子)得以驗證,但是“微分漲落定理”的實驗驗證卻一直是一項巨大的挑戰,因為測量膠體粒子的瞬時速度對實驗技術提出了極高的要求.2017年,本文作者之一和美國普渡大學的李統藏教授研究組[47]合作,借助他們發展出來的超高時空分辨的光力系統實驗平臺,測量了束縛在空氣中的納米小球在激光驅動時位置和瞬時速度隨時間的演化.通過獲取大量軌道數據,第一次在實驗上驗證了這個被稱為漲落定理之母的“微分漲落定理”.這項工作將隨機熱力學實驗研究從過阻尼情形拓展到了欠阻尼情形,并且把這個最基本的漲落定理乃至所有其他的有關非平衡功的漲落定理都建立在了堅實的實驗基礎之上.

值得指出的是,在這些漲落定理中,越粗粒化的發現得越早,越精粒化的發現得越晚.考慮到漲落定理是對熱力學第二定律的不同形式的推廣,不難得到如下結論: 物理學家對熱力學第二定律的認識也是循序漸進,逐步深入的.這一點與物理學家對原子結構的認識過程非常相似.

除了與功有關的漲落定理,還有一個有關熱交換的漲落定理[48],它描述的是一個初始時處于溫度βs的系統跟一個處于溫度β的熱庫在接觸過程中熱交換滿足如下的恒等式[48]:

其中Q是系統從熱庫吸熱.利用Jensen 不等式,可以得到

(15)式為Clausius 不等式,只能從相對的高溫熱源吸收熱量.如果把有關做功和熱交換的漲落定理合并起來考慮,可以得到一個多熱庫時的,關于功和熱的聯合分布的漲落定理[49]:

式中βν是第ν個熱庫的溫度;?F是系統的自由能之差.這個多熱庫的漲落定理可以分別回到Jarzynski 恒等式,或者有關熱交換的漲落定理.因此,可認為這個不等式是有關做功和熱交換的漲落定理的最一般的形式,它將所有關于非平衡做功和傳熱的漲落定理統一在一個公式里.有關詳細內容見文獻[49].

以上關于功和熱的漲落定理都是在細致平衡條件成立時的結果.當細致平衡條件不成立時,還有其他一些漲落定理: 比較知名的有Evans-Searles 漲落定理[50,51]和Gallavotti-Cohen 漲落定理[52,53].從這些細致平衡條件被破壞的漲落定理出發,還可以推導出所謂的熱力學不確定性關系[54,55].由于篇幅所限,對這些內容不再詳述.

3.2 量子漲落定理

研究人員最初對有關隨機熱力學和漲落定理的研究主要聚焦于經典系統,此后開始思考將熱力學的理論框架和漲落定理推廣到量子系統.向量子力學的推廣并不是非常直接的,因為量子系統的微觀狀態用Hilbert 空間的矢量表示,而經典系統的微觀狀態用相空間的一個點代表.另外,量子系統里的測量、波函數塌縮、量子軌道等概念與經典系統具有明顯的區別.經典粒子在相空間有很好定義的軌道,從而可以定義軌道功、軌道熱等概念,但由于量子不確定性原理,對量子系統不能很好地定義軌道.這些區別給量子隨機熱力學和量子漲落定理的研究帶來了挑戰.下面簡要介紹把隨機熱力學和漲落定理向量子系統的推廣.

量子孤立系統是指在驅動過程中,系統不與外界熱庫發生相互作用,所以沒有熱交換.在量子孤立系統中,系統的幺正演化算符為

其中T是編時算符.在整個驅動過程中,外界對系統會做功W.由于是量子孤立系統,過程中并沒有與熱庫的熱交換,那么做功值便是演化前后的能量差.標準的量子功的定義是基于兩次能量投影測量(two-projective energy measurement,TPM),2000年由Kurchan[56]和Tasaki[57]分別獨立提出.即在初始時刻時先做一次能量投影測量,譬如系統的態塌縮到了初態哈密頓量的第m個能量本征態,然后從這個能量本征態開始演化,在終止時刻時再進行一次能量投影測量,這時系統的態可能塌縮到了末態哈密頓量的第n個能量本征態,整個過程稱為一次實驗.在這次實驗中,能量差W便被定義為量子功.當然可以重復很多次實驗,每次得到的功的值都可能不一樣,最后便有一個功分布P(W).整個過程的示意圖見圖8.

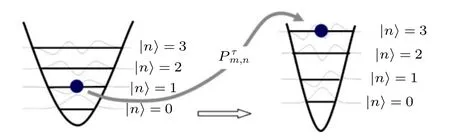
圖8 基于兩次投影定義的軌道功.這里顯示了一次實驗的結果,從第2 個本征態跳到第4 個瞬時本征態Fig.8.Trajectory work based on two-point measurement.This figure illustrates a trajectory: from the 2nd to the 4th instantaneous eigenstate.

基于 TPM 的量子功的定義最大的好處是滿足量子 Jarzynski 恒等式[56–58],形式與經典情形下的 Jarzynski 恒等式(13)式完全一致,成立條件仍需要初態為熱平衡態:,其中Z0為初始時刻的配分函數量子Jarzynski 恒等式的簡單證明如下[56,57]:

2013年兩個研究組[59,60]提出間接驗證量子Jarzynski 恒等式的方案——將功分布的傅里葉變換映射為一個量子開放系統的退相干因子.通過測量這個退相干因子間接獲得功分布的信息.這個方案最終在2014年被實驗驗證[61].量子Jarzynski恒等式的直接實驗驗證由本文作者之一與清華大學金奇奐教授[62]合作完成.通過發展一種適用于單離子的聲子投影測量技術,最終實現了對量子力學系統做功的測量,并成功驗證了量子Jarzynski恒等式.這個工作在非平衡統計物理領域產生了一定的國際影響.

在經典力學和經典熱力學中,功的定義非常清楚,但相應的量子力學的做功一直困擾著物理學家.2000年,Jarzynski 剛提出他的恒等式不久,法國物理學家Kurchan[56]和日本物理學家Tasaki[57]就很快將Jarzynski 恒等式推廣到了量子力學系統.不過,他們為了得到這個量子Jarzynski 恒等式,引入了一個非常反直觀的基于兩次投影定義的量子軌道功的概念,而量子投影意味著波包塌縮假設,這在量子力學中是有爭議的.從2000—2015年,量子軌道功的定義和內涵一直是研究的焦點,但幾乎沒有任何進展.

2015年,本文作者之一和合作者[63]對這個非平衡統計物理的重要問題——量子力學軌道功的定義和內涵進行了深入研究,利用半經典力學的辦法,第一次嚴格解析證明了量子軌道功滿足量子力學“對應原理”,并第一次揭示了量子力學的軌道功和經典力學的軌道功的聯系.這為基于兩次投影方法定義的量子軌道功找到了一個佐證,從而在一定程度上證明了基于兩次投影定義的量子軌道功的合理性.2018年本文作者之一和合作者Ken Funo[64]又進一步把上述工作向前推進.首次將路徑積分方法引入到量子開系統的熱力學研究中.具體說來,該項研究引入了一種全新的辦法(定義單條費曼路徑上的軌道功),從而可以更好地闡明量子軌道功和經典軌道功之間深刻的內在聯系,而且可以很方便地把功分布的對應原理從原來的孤立系統推廣到量子開放系統.

在平衡態統計物理中,統計配分函數包含了熱平衡態的重要信息.因此發展各種解析和數值方法計算一個物理系統的配分函數成為平衡態統計物理研究的重要內容.與之類似,對于一個非平衡驅動過程,它的功分布函數和熱分布函數包含了有關非平衡過程的重要信息.發展各種方法計算非平衡過程的功分布和熱分布函數稱為非平衡統計物理研究的重要內容.筆者團隊在這個方面也進行了一些探索.我們計算了活塞中單個布朗粒子在等溫過程的功分布[65],腔量子電動力學系統[66]及有相互作用的量子多體系統[67]在絕熱過程的功分布.此外,還用路徑積分方法研究了量子開系統的軌道熱滿足的漲落定理[68,69],以及具有對偶關系的一維玻色系統與一維費米系統的做功的全同性[70],這種對偶性也會體現在以這些量子多體作為工作物質的量子熱機的效率[71].這些研究顯著拓展了對量子系統做功的理解.

4 統計熱力學廣義正則熱化理論與黑洞信息佯謬

近些年來,量子信息的發展使得人們對量子糾纏有了更加深入的理解,從新的角度開展了統計物理理論基礎的創新研究.統計物理學的一個基本假設是等概率假設,并由此發展出基于微正則系綜、正則系綜以及巨正則系綜的統計熱力學理論.通常的教科書從熱庫加系統構成的微正則系綜假設出發,推導出系統的正則系綜(吉布斯)分布.近些年這方面的研究表明,可以不基于上述等概率基本假設,而直接利用量子糾纏的觀念,建立正則系綜(吉布斯)分布[72–74].

我們把系統之外的部分統稱為環境,以區別于通常有溫度的熱庫.整個系統(系統加環境)的波函數通常是一個糾纏態.在我們的模型中[75],系統是一個個多能級的系統,其基矢量 |n〉對應能級為εn(n=1,2,···);環境由N個模式頻率為{ωj}的諧振子構成(aj是j模式的消滅算子).二者之間的“最小”相互作用為系統的本征能量為對于環境和系統組成的整體系統,其能量被限制在一個變形能殼上,如圖9 所示.

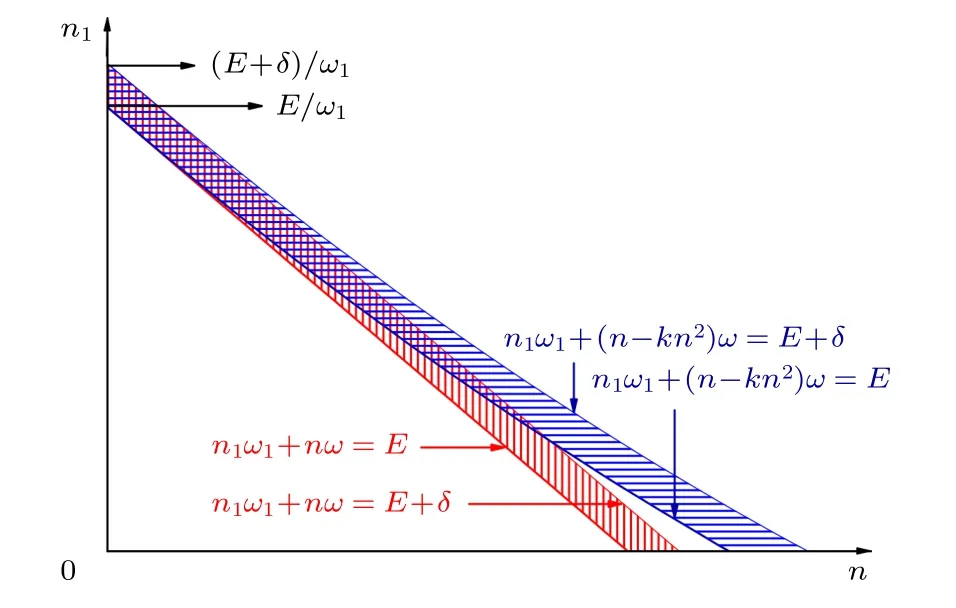
圖9 能殼變形圖,其中紅色是無相互作用的能殼,藍色為有相互作用的修正Fig.9.The distortion of the energy shell,the red area shows the case with no interaction,and the blue one shows the case with weak interaction.

系統的狀態可以通過整體能殼上純態|ψ〉=約化掉環境自由度得到,即ρS=可以證明Fnm具有因子化結構,并且在環境自由度足夠大的時候趨近于零,即Fnm→0.根據概率論中的大數定律,可以證明對角項的平均值為,其中?(E-εn,δ)是環境在能殼[E-εn,E-εn+δ] 上的狀態數.對于諧振子環境,可以得到

該分布在環境維數足夠大的時候近似于正則吉布斯分布,其中溫度為.

上述模型說明,在系統加環境的波函數集合中,絕大多數純態波函數給出的系統約化密度矩陣在熱力學極限下都滿足正則分布.其實,對于宇宙中一個足夠小的子系統,當整個宇宙處于任意一個純態時(不必是等概率分布的混態),這個子系統幾乎都近似地處于熱平衡態.這種現象被稱為“廣義正則原理”(general canonical principle)或“正則典型性”(canonical typicality).這樣就可以將量子統計力學完全建立在量子力學的基礎之上.

在廣義正則熱化研究中,系統和環境之間的糾纏會扮演重要的角色.如果系統和環境處于簡單的直積態上,約化后的系統狀態不會是正則系綜的Gibbs 分布.因此,滿足廣義熱化的狀態一定是系統和環境之間的糾纏態.文獻[72—74] 研究的系統和環境之間無相互作用,而筆者團隊的工作證明相互作用的出現使得等能殼層變形.在變形的等能殼層內,對環境取平均得到的系統約化密度矩陣不再是正則的,變形會使得在小系統的熱化態上產生一個灰度因子[75],影響約化系統的溫度.

廣義正則熱化的一個重要應用是解釋黑洞非熱輻射譜和黑洞信息丟失之謎.2000年Parikh 和Wilczek[76]利用隧穿理論得到小質量Schwarzschild 黑洞的非平衡輻射譜.質量為M的黑洞輻射能量為ω的粒子后,質量M改變為M-ω會影響輻射后的時空度規,并直接影響再輻射的概率分布,導致非正則熱態:

則輻射分布不僅與黑洞質量有關,還與輻射粒子本身的能量有關.后來蔡慶宇等[77,78]發現,這種非熱分布實際上包含了輻射粒子之間的關聯信息,可以用來解釋黑洞信息丟失之謎.他們計算了能量分別為ω1和ω2的兩次輻射之間的關聯熵S(ω1:ω2)=8πω1ω2,其中單次輻射熵S(ω)=-lnΓ(ω).這意味著從黑洞視界先后輻射出的粒子之間存在關聯,關聯大小正比于兩個粒子的能量.在此基礎上可以得到黑洞輻射的級聯公式:

其中S(ω2|ω1)是條件輻射熵.可以證明,當黑洞完全輻射掉時,輻射的關聯熵就是原初的黑洞熵,S(ω1,ω2,···,ωn)=4πM2.因此,基于上述關聯信息可以解決黑洞輻射中的信息丟失問題,即黑洞輻射丟失的信息完全轉化為輻射粒子間的關聯 .

仔細分析蔡慶宇等[77]的開創性工作,本文兩位作者意識到如此復雜的黑洞度規給出的輻射粒子之間關聯方式居然都相同,平衡情況輻射的非正則形式一定與黑洞的時空幾何無關.基于非正則熱化的工作,他們與蔡慶宇合作,從黑洞的“一毛”定理出發,兩次級聯輻射(先后能量為ω1和ω2)和一次能量為ω1+ω2單輻射的等價性,一般地推導出了黑洞輻射的非正則分布Γ(ω)[78].研究分析還把黑洞的自由度B和時空其他部分O考慮成為熱化環境.假設整個宇宙處在一個純態:

黑洞的狀態即是ρB=TrO[|Ψ〉〈Ψ|],根據前面廣義熱化的討論可以知道黑洞的狀態近似為一個熱態.再把輻射本身當作研究熱力學系統,根據廣義正則熱化的思想,就能一般地得到黑洞輻射能譜的非熱分布[79].這一研究表明,輻射-黑洞關聯導致的黑洞非熱輻射譜是有限系統統計的必然結果.

需要指出的是,系統加環境的整個態空間中,還存在一部分不滿足正則典型性的狀態.近些年來,關于本征態熱化假說(eigenstate thermalization hypothesis)的研究[80,81]探討了系統如何從這部分不滿足正則典型性的少數狀態演化到滿足正則典型性的狀態,為有限系統熱化問題的研究提供了嶄新的思路.

5 有限時間熱力學

熱力學發展的另一個維度是時間變得有限.在傳統的熱力學的研究中,很少關注時間維度.例如,傳統熱力學循環中的等溫過程通常是準靜態過程、無法包含演化過程,傳統教科書通常也不會提及等溫過程中時變參數是按照如何的方式進行變化的.熱力學循環既是熱力學研究的開端,又是熱力學的一個重要應用.熱力學循環通過周期性過程從高溫熱源提取熱能并將其部分轉化為可以使用的能源,如機械能.以熱力學循環為基礎的熱機引起了第一次工業革命.圍繞熱力學循環的研究,總結出了熱力學三大定律.其中最為重要的熱力學第二定律表明,熱力學循環能量轉化效率是有上限的,即Carnot效率,它是通過理想Carnot 循環來實現的.

理想Carnot 循環給出了所有熱力學循環效率的基本限制,杜絕了一大類永動機的嘗試,是熱力學發展的里程碑.Carnot 循環是建立在一組準靜態過程基礎上的熱力學循環,其中在兩個分別與高、低溫熱源接觸的等溫過程中,要無窮緩慢地操控氣體體積,Carnot 循環需要的時間原則上是無窮長,這使得理想Carnot 循環的在單位時間內輸出為零,即功率為零.然而,在實際的應用中,通常最大的需求是熱力學過程有較大的輸出功率,例如我國最新裝機的石島核電站的一個關鍵指標是裝機功率.針對這一類問題,有限時間熱力學應運而生,其核心目標是彌合理想的傳統熱力學理論和實際應用之間的鴻溝,并推動非平衡熱力學的發展,對近平衡過程給出定量的結果.

5.1 功率-效率約束關系

有限時間熱力學的發展肇始于核電能源的發展.在20 世紀50年代,Yvon[82]針對核電循環得到了最大功率輸出時的效率.1975年,針對有限時間的Carnot 循環,Curzon 和Ahlborn[83]利用恒定熱力學流的假√設,得到了后來廣為人知的CA效率,.值得注意的是該效率不依賴于循環中物質的特性,具有相當的普適性,因而得到了廣泛的關注,并在20 世紀七八十年代引發了有限時間熱力學研究的熱潮[84,85].

有限時間熱力學過程通常伴隨著額外熵(即不可逆熵)產生,時間越長額外熵產生越少.在近些年發展的低耗散模型[86]中,工作物質在兩個有限時間等溫過程中吸收的熱量表達成如下:

其中 ?S是系統從高溫熱源吸收熱量帶來的可逆熵變化,而Σh/τh和Σc/τc代表不可逆的熵產生.額外熵產生這種最簡單的 1/τ標度關系,通常被稱為低耗散假設.值得注意的是,后來的很多模型采用這種標度假設,例如有限時間量子Carnot 循環.基于低耗散模型,有限時間Carnot 循環中功率輸出為P=(Qh+Qc)/(τh+τc).在功率最大 (?P/?τh=?P/?τc=0)時,該循環效率存在一個上限ηEMP=ηC/(2-ηC),即最大功率效率,它不依賴做功物質性質.值得強調的是,這個最大功率效率可以在Σh?Σc時得到.

對于任意給定的輸出功率P,有限時間Carnot循環的效率不僅存在上限,而且還存在下限.我們[87]推導出一般得到效率和功率約束關系:

圖10 有限時間Carnot 循環的功率效率約束關系 (a)基于二能級系統的有限時間量子Carnot 循環;(b)量子Carnot 循環中功率-效率和一般約束關系的對比,其中圖中的棕色虛線和灰色點線是由(25)式給出,綠色三角代表最大功率的位置Fig.10.The power-efficiency constraints of a finite-time Carnot cycle: (a)Finite-time quantum Carnot cycle based on a two-level system;(b)comparison between power-efficiency and general constraint relationships in a quantum Carnot cycle,where the brown dashed line and gray dotted line in the graph are given by Eq.(25),and the green triangles represent the positions of maximum power.

在傳統的準靜態熱力學循環中Carnot 循環的效率最高,但在有限時間熱力學過程中該結論不再成立.可以證明,在二者都在最大功率條件下,Otto 循環的效率在一些參數區間內會明顯優于Carnot 循環.特別在溫差較小的情況下,通過Otto熱力學循環更容易獲得更高的效率[90,91].低耗散模型之所以能在近些年掀起有限時間熱力學研究的新潮流,是因為此模型能夠把外界的控制方式和動力學演化納入熱力學研究的框架中[92].在有限時間等溫過程中,與不可逆熵產生關聯的參數Σh和Σc與控制的過程直接相關.對于二能級量子系統,參數Σh=Θξ,其中與系統初末狀態參數以及環境溫度有關,ξ=〈v2〉/〈v〉2與參數控制速度v的漲落相關.此后,有更多的研究將熱力學過程控制納入有限時間熱力學的研究中,其中蘊含了后文提及的熱力學長度等概念.

5.2 有限時間熱力學實驗

有限時間熱力學的研究取得了大量的研究成果,它們在很大程度上使用了前述的低耗散模型假設,即不可逆熵的 1/τ標度關系.在物理上,低耗散模型和熱力學系統線性相應理論是等價的,因此1/τ標度關系是長時近似的結果[93].有限時間熱力學的理論和實驗必須關注該標度關系在多大范圍內適用.其實近期理論上有很多的研究從運動方程出發,給出了標度關系的成立區間,但是在實驗上卻鮮有這方面的研究成果,究其原因是實驗平臺的缺乏.最近,在一些微觀實驗的平臺上[20],已有少數實驗開始關注有限時間熱力學.

3年前,我們[94]基于理想氣體搭建了一個有限時間熱力學實驗平臺.實驗裝置中的工作物質是干燥空氣,其狀態由理想氣體狀態方程描述.有限時間熱力學過程通過步進電機進行精確控制.對于理想氣體而言,一旦獲得氣體的壓強P和體積V,就可以計算出氣體的溫度T,進而獲得氣體的內能變化.

通常可以用不可逆做功來度量有限時間過程的不可逆性,Wirr(τ)=W(τ)-?F,其 中 ?F是系統的自由能的變化.當操控速度遠大于氣體的弛豫速率,即,不可逆做功也具有 1/τ關系.其中γ是氣體的絕熱系數,tr是氣體的熱弛豫的特征時間.圖11 展示了在溫度為50 ℃下壓縮理想氣體做功隨過程時間τ的變化關系,實驗數據證實,長時間可逆做功隨時間按照1/τ標度關系衰減;不可逆熵做功可以通過壓縮空氣的方式來改變,在時間一定的情況下,勻速地壓縮過程中不可逆做功明顯低于以多項式方式壓縮氣體的做功.這個結果表明,有限時間熱力學過程的操縱方式對于調節熱力學過程十分重要.因此,這個研究工作為優化熱能源轉化過程提供了新思路.

圖11 有限時間熱力學 1/τ 關系的實驗驗證 (a)溫度50 ℃下做功的 1/τ 標度關系;(b)標度關系的系數對操控方式的依賴關系 L (t)=L0 ∝tα,能量損耗最優操控是勻速控制α=1Fig.11.Experimental verification of the finite-time thermodynamic 1/τ relationship: (a)The 1/τ scaling relationship for work done at a temperature of 50 ℃;(b)the dependence of the scaling relationship coefficient on the control method L (t)=L0 ∝tα,with the energy-optimal control being uniform-speed control where α=1 .

近些年熱力學實驗的一個重要方向[95–97]是驗證有限時間熱力學循環過程的功率和效率約束關系.基于搭建的理想氣體的有限時間熱力學平臺,我們[98]設計完整的有限時間Carnot 循環,并定量地驗證了功率-效率約束關系.循環中兩個等溫過程分別在不同的溫度的熱浴中完成,在測得相應的做功和吸放熱的同時,保證了等溫過程的末態和另一個等溫過程的初態通過一個絕熱過程連接起來,實現了有限時間Carnot 循環.圖12 展示了有限時間Carnot 循環的過程和熱力學循環的功率-效率約束關系.評估有限時間Carnot 循環的關鍵量是最大功率效率.我們提取了實驗中所有溫度組合的最大功率效率,并在圖12(c)中展示其與Carnot效率的關系.獲得的最大效率(帶有誤差棒的標記)遵循一個簡單的關系ηEMP=(0.524 ± 0.034)ηC.它與各種有限時間循環模型的最大功率效率在Carnot 效率ηC的一階項上很好地符合.例如,在CA模型中ηCA和低耗散模型[86]的ηC/(2-ηC)中,系數1/2 是一個獨立于特定特征的線性響應區域的普遍值[99].我們的實驗數據精確地確認了1/2 系數的存在.

圖12 有限時間Carnot 循環 (a)有限時間Carnot 循環的工作 示意圖;(b)循環中功率-效率約束 關系;(c)最大功率效率對Carnot 效率的依賴關系ηEMP=(0.524 ± 0.034)ηCFig.12.Finite-time Carnot cycle: (a)Schematic diagram of the finite-time Carnot cycle;(b)graph of the power-efficiency constraint relationship in the cycle;(c)dependency of maximum power efficiency on Carnot efficiency ηEMP=(0.524 ± 0.034)ηC.

5.3 有限時間熱力學的幾何描述

如前文所述,在有限時間熱力學過程中,產生的不可逆性是評估熱力學過程非平衡的一個重要指標.通常可以使用不可逆熵產生來衡量,例如在一個熱化的過程中,不可逆的熵產生隨時間單調遞增.低耗散模型假設在熱交換過程中不可逆熵的變化滿足 1/τ標度關系.對于直接可測量物理量,不可逆做功也存在 1/τ標度關系.傳統熱力學和統計物理的研究表明,非準靜態過程對體系做功會超過體系的自由能變化,即W≥?F.近年有限時間熱力學研究把此不等式替換成一個定量的關系W=?F+C/τ,其中C≥0 是與系統初末態以及操控方式有關的參數[32].

事實上,上述定量的關系在有限時間熱力學過程研究中至關重要,它牽涉到一個控制過程中時間和能量損耗的制約關系,必然涉及二者之間的優化匹配問題.給定控制時間τ,我們關心的是在多大程度上能夠減小能量損耗,以及相關的理論極限問題.這個問題研究可以追溯到早期關于平衡態熱力學距離問題,即非平衡過程的能量損耗極小值怎么受限于平衡態空間的幾何屬性.對于緩慢調控(但非準靜態)的等溫過程,系統在演化過程中的每一個瞬間都接近于熱平衡態,它可以近似地由一組系統的平衡態參數描述,比如系統的壓強和溫度.在這樣近平衡區域的近似下,不可逆程度將普適地反比于調控時間,可以通過幾何的語言描述,這就導致了熱力學長度的概念[100].在幾何上[101,102],熱力學“距離”有明確的物理意義: 在近平衡的緩慢驅動下,初末態間的熱力學長度給出了在有限時間內完成等溫過程所消耗的不可逆功下限[103–106].

為簡單起見,以理想氣體為例,說明平衡態空間距離和非平衡過程不可逆性之間有特定的約束關系.束縛在一個體積為V的理想氣體的相空間分布滿足Maxwell 分布.對于體積不同(Vi和Vf)的兩個分布,通過Fisher 信息度規gVV定義兩個分布之間的距離:

再考慮溫度為Te的環境中理想氣體,從Vi變到Vf,在慢速控制下的不可逆功為

其中CV是等容比熱,γ是熱傳導系數.利用變分原理可以得到在時,不可逆做功達到最小值,即Wirr,min∝D2.從這個簡單的例子看出,最小不可逆做功和平衡態分布的距離有關,以下將對一類熱力學過程[107]精確給出這種聯系.

為了評估平衡熱力學系統中特定控制參數的影響,要保證系統在參數調控完成之后仍然處在平衡狀態上.這個過程是一個等溫過程,在理論和實際應用中都至關重要.然而,實現等溫過程的傳統方案是準靜態過程,因此需要無限長的驅動時間.當評估的時間小于系統弛豫時間,傳統調控弛豫的方案無法使用.因此加速系統演化并保證系統參數調控完成之后達到平衡態是有限時間熱力學中的挑戰性問題.接下來一個非常自然而又與應用緊密相關的問題是: 是否能夠構造一種方案,加速實現等溫過程,在有限時間內將系統從一個平衡態快速轉換到另一個等溫平衡態? 等溫捷徑(shortcuts to isothermality)的方法就是一種加速等溫過程的手段,實現等溫平衡態之間的有限速率轉換[108].

考慮一個物理系統,其哈密頓量為Ho(x,p,λ).我們希望施加輔助控制,使得在給定的時間τ,把參數λ從λi調控到λf下,并保持系統始終處在熱平衡態上.此時系統拓展為由新哈密頓量H0+Ha描述的新系統.在起始和末了時刻,將輔助勢場Ha(t)撤除,Ha(0)=Ha(τ)=0 .這樣使得擴展系統的哈密頓量H0+Ha結束時恰好回到原來的哈密頓量H0.同時在初始和末了時刻,系統分布函數恰好就是相應哈密頓量對應的平衡態.在這個過程中,不可逆做功寫成嚴格的二次型形式:

此時定義描述不可逆做功的度規為gμν=,可以證明該度規是正定的.根據Cauchy-Schwarz不等式,最小不可逆功是Wirr,min=L2/τ,其中是兩平衡態間的距離,即熱力學長度.

值得指出的是,熱力學長度包含了一些動力學的參數,但與動力學過程無關,不依賴于參數的具體控制方式.在這一數學框架下,尋找能量消耗最小的優化控制方案等價于求解黎曼幾何空間中的測地線方程(如圖13 所示).于是,就可以利用微分幾何學的方法求解熱力學中的最優控制問題,比如,利用捷徑方法優化布朗熱機的功率[109].需要提及的是,最近也有一些研究中定義了依賴于時間的“度規”,當然不具有嚴格的空間幾何屬性[110].

圖13 能量最小消耗路徑的幾何描述Fig.13.Riemann geometry for the minimum energy cost.

建立熱力學長度和非平衡過程不可逆性之間的聯系,是有限時間熱力學中近些年的一個重要進展,它把傳統熱力學的做功和自由能關系W≥?F拓展為W≥?F+L2/τ,使得人們能夠通過熱力學長度找到能量損耗的下限,通過尋找幾何測地線則能找到達到下限的操控方式.目前,研究熱力學的幾何方法已經被用來設計優化能量使用的具體方案[111–115],如用熱力學幾何構造信息擦除[111–113]和膜分離氣體[114,115]的最小能量損耗方案.

6 結論

總而言之,時空尺度有限的小系統統計物理和熱力學研究已經成當代物理發展的重要前沿領域,它整體上可以用本文介紹的介觀統計熱力學進行概括和總結.其中,作為熱力學第二定律的“升級版”,漲落定理(由此可以推導出熱力學第二定律)是研究各種問題的關鍵,而有限系統的非正則平衡分布則內置了二階漲落.

介觀統計熱力學與量子物理,能源物理以及信息科學結合,催生了一些重要的研究分支.這方面研究結果不僅豐富了統計熱力學的內涵,而且為建立一般性的遠離平衡的統計熱力學理論框架帶來了新的啟示.這方面研究結果還可以應用到能源的產生與轉化以及光合作用的應用領域.我們相信,未來介觀統計熱力學的發展將會在一些重大科學問題上取得突破,逐步走向實驗和實際應用.