莫特物理
——量子材料的主旋律之一*

封東來

(中國科學技術大學核科學技術學院,國家同步輻射實驗室,新基石實驗室,合肥 230027)

1 引言

游牧民族和農耕民族之間的戰爭貫穿了人類社會的歷史.遷徙與定居兩種不同社會形態的競爭和融合,產生了豐富的社會形態和歷史文化.量子材料具有非常豐富的現象,著名凝聚態物理學家P.W.Anderson 的宣言“More is different”便指出了量子材料的復雜性來自于多粒子體系的演生現象(emergent phenomena).與人類遷徙與定居兩種社會形態類似,量子材料中電子巡游性(itinerancy)與局域性(localization)之間的競爭,又被稱作莫特物理(Mott physics),是很多演生現象背后的機制.兩個極端的情況是巡游性主導的金屬與局域性主導的莫特絕緣體.莫特相變就是一種金屬-絕緣體相變,描述這一物理現象的哈伯德模型(Hubbard model)或者t-J 模型,就是由描述電子巡游性的t(動能項),和描述局域相互作用(勢能項)的U構成的.

動能和勢能本就是描述量子體系的薛定諤方程中的主要兩項,如圖1(a)所示.動能項是對電子波函數在空間上的二階導數,于是在基態中,如果希望這一項的能量盡可能小,就要求波函數更延展,即電子更巡游.而在深勢阱中,勢能最小化則要求電子波函數局域在勢阱內,因為勢阱外部勢能大(圖1(b)).這樣兩項的競爭就導致了電子既不可能無限延展,也不可能很局域.

圖1 (a)薛定諤的貓和方程;(b)一維勢阱模型Fig.1.(a)Schr?dinger’s cat and equation;(b)the model of one-dimensional potential well.

巡游和局域,或者動能與勢能,這兩者之間的競爭與合作無論是對于簡單的量子體系還是復雜的量子材料都是最根本的機制.本文的主要觀點就是眾多量子材料復雜表象下的本質(How is more different?),大多可歸結為電子巡游性與局域性之爭,這也是量子材料微觀機制的主旋律(main theme)之一.特別是在d 和f 軌道電子主導的體系中,巡游或局域各自都無法主導另一方,因而體系表現出豐富的物性.下面將分六小節來闡述這一觀點,其中部分例子來自我們課題組的一些工作.

2 莫特物理及其兩條相變路徑

在莫特的思想實驗中,一個氫原子鏈上,每個原子有一個電子,如圖2(a)所示.根據能帶理論,這會形成半占據的能帶,基態是金屬.但是莫特考慮當原子間距越來越大時,電子在原子間跳躍(t,動能)總歸要小到可以忽略,該體系最終要成為絕緣體,在這種極限下,當兩個電子處在同一個原子時,它們之間的庫侖排斥引起的勢能U要遠大于t引起的動能降低(參考量子阱的例子).在理論上人們可用哈伯德模型來描述這個思想實驗,其哈密頓量是:

圖2 (a)一維氫原子鏈模型;(b)哈伯德能帶示意圖,下哈伯德帶(lower Hubbard band,LHB)是填滿的,上哈伯德帶(upper Hubbard band,UHB)是空帶;(c)二維哈伯德模型Fig.2.(a)One dimensional hydrogen atom chain model;(b)the schematic illustration of Hubbard bands,where the lower Hubbard band (LHB)is filled,and the upper Hubbard band (UHB)is empty;(c)two-dimensional Hubbard model.

其中σ=↑,↓是電子自旋;是第i個位置的占據態電子數算符.當U大于能帶寬度W時,該體系的能帶由上下哈伯德帶構成,下哈伯德帶填滿,上哈伯德帶為空,體系成為了絕緣體(圖2(b)).二維體系的哈伯德模型如圖2(c)所示,其物理圖像和一維情形類似.

調控莫特相變的途徑有兩種,如圖3(a)所示.隨著U/t參數的改變,體系發生了金屬-絕緣體相變(MIT),此類相變被稱作帶寬調控的莫特相變(bandwidth control,BC-MIT).還有一種占據調控途徑(filling control,FC-MIT),即通過摻雜來引入載流子,這樣能帶也可成為部分占據,從而使得絕緣體變成了金屬.當然,載流子摻雜還使得電子在格點間躍遷更加容易,即有效的動能項(t)增加,電子之間的關聯減弱,進一步產生了部分帶寬的改變[1].

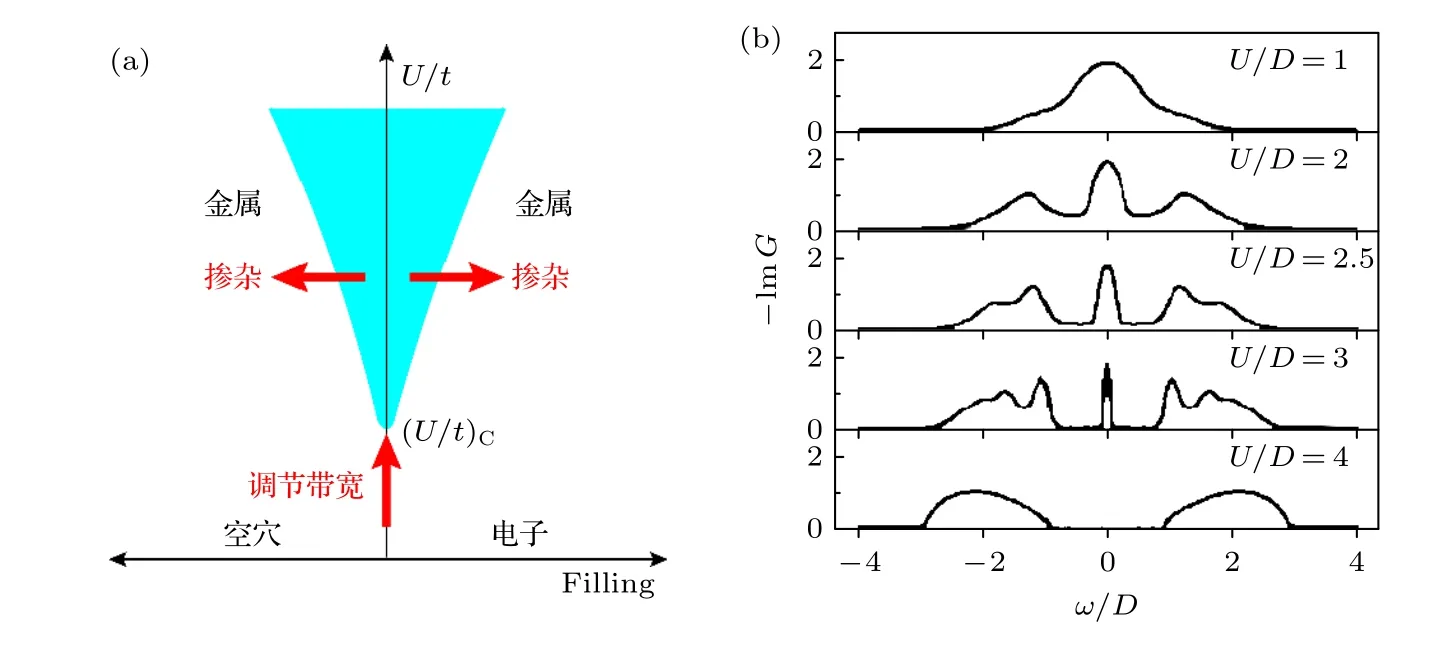
圖3 (a)莫特相變的兩種途徑.考慮雜質局域勢場影響以及有限體系尺寸,相圖中的絕緣態隨著摻雜的相轉變邊界是位于有限的摻雜濃度下的.(b)動力學平均場計算模擬出的Hubbard 模型,在T=0 時,不同強度U 下的局域譜函數展示了帶寬調控莫特相變的過程 (D=W/2,W 是能帶寬度)[1]Fig.3.(a)Two routes of Mott phase transition.Considering the influence of impurity local potential and the finite system size,the phase boundary is located at a finite doping concentration.(b)The spectral functions of the Hubbard model calculated by dynamic mean field theory at different U (T=0),demonstrating the process of bandwidth-control Mott phase transition (D=W/2,W being the bandwidth)[1].

動力學平均場(dynamical mean field theory,DMFT)的計算結果很好地描述了BC-MIT 的過程,如圖3(b)所示.從莫特絕緣體出發,隨著U逐步減小,在帶隙中出現了準粒子,其譜權重逐步增加,準粒子帶的帶寬逐步變寬,最終連接上下哈伯德能帶,此時體系變成普通的半滿金屬.而Brinkman-Rice 則反過來從金屬出發,逐步地增加U,隨著電子關聯增強,準粒子帶寬減小,換言之,準粒子的有效質量越來越大,最終重到準粒子再也動彈不得,相干的準粒子譜重小到忽略不計,體系就進入了莫特絕緣體狀態.莫特圖像和Brinkman-Rice 圖像是等價的.

3 占據調控莫特相變示例

載流子摻雜形成的銅氧化物高溫超導就是典型的FC-MIT,其母體是反鐵磁絕緣體,隨著少量的電子或空穴摻雜,體系就進入了超導態.雖然銅氧化物高溫超導的機理仍然有爭議,人們一般認為反鐵磁漲落引起了d 波超導配對.而隨著載流子濃度的進一步提高,電子關聯逐步減弱,超導配對逐步減弱,直至成為費米液體金屬.

銥氧化物Sr2IrO4是個絕緣體,晶體結構和La2CuO4相似,由于存在較強的自旋軌道耦合,其反鐵磁基態可以等效地用總角動量J=1/2 的哈伯德模型描述(圖4(a))[2],且t和U等參數大約是銅氧化物的一半,因此人們預言摻雜的Sr2IrO4是一個轉變溫度(Tc)約為銅氧化物一半(40 K 左右)的d 波超導[3].

圖4 (a)考慮自旋軌道耦合和Hubbard U 情況下,5d5 態的能級示意圖,展示了總角動量Jeff=1/2 的莫特絕緣體基態;(b)0.5 ML(monolayer)鉀原子覆蓋下的Sr2IrO4 的費米面結構 (T=70 K)[5];(c)不同摻雜量的鉀原子覆蓋下的Sr2IrO4 的能隙隨動量(費米面角)的依賴關系[5];(d)0.6 ML 鉀原子覆蓋下的Sr2IrO4 表面的電子態在E=20 meV 下的分布圖(T=20 K),展示了不均勻的能隙分布情況[4];(e)圖(d)中不同區域的典型隧道譜[4]Fig.4.(a)Schematic diagram of the 5d5 states,considering spin orbit coupling and Hubbard U,where the ground state is a Mott insulator with a total angular momentum of Jeff=1/2;(b)the Fermi surface of Sr2IrO4 covered by 0.5 ML (monolayer)potassium atoms (T=70 K)[5];(c)the energy gap as a function momentum (Fermi surface angle)for K-dosed Sr2IrO4 with different potassium coverages[5];(d)the local electronic density-of-states map at E=20 meV for the Sr2IrO4 surface covered by 0.6 ML potassium atoms shows an uneven distribution of energy gaps (T=20 K)[4];(e)typical tunnelling spectra in different regions in Figure (d)[4].

最近,通過在Sr2IrO4表面蒸鍍鉀原子或插層的方法引入電子摻雜,人們利用掃描隧道顯微鏡(scanning tunneling microscopy,STM)[4]和角分辨光電子能譜儀(angle-resolved photoemission spectroscopy,ARPES)[5]都觀察到了表面層中發生了絕緣體-金屬轉變.如圖4(b)所示,其費米面和單層銅氧化物的費米面形狀相似,只不過它是電子型的.低溫下,ARPES 也觀察到了能隙在對角線方向有節點,隨著偏離對角線方向,能隙逐步變大,顯示出類似d 波的行為,如圖4(c)所示.在STM的研究中,人們發現其電子態的微觀不均勻性與銅氧化物也非常類似.比如在不同區域看到了V 型類超導能隙、贗能隙、絕緣體能隙等現象,如圖4(d)和圖4(e)所示,這些都表明了d 波超導的跡象.但是,由于這些跡象都發生在摻雜的樣品表面層中,輸運測量非常困難,所以人們至今尚未證實體系是否真的處在超導態.從這些研究中可以看出,這個體系的確展現了占據調控的莫特相變,乃至可能引發超導配對等現象.

4 帶寬調控的莫特相變示例之一:NiS2–xSex

NiS2–xSex是一個典型的帶寬調控的莫特相變體系,Se 取代S 是同價摻雜,只提供了化學壓力,其相圖與加物理壓力的相圖幾乎一致[6].隨著Se的含量逐步增加,在x約為0.4 附近有一個從反鐵磁絕緣體到反鐵磁金屬的莫特相變.在圖5(a)的ARPES 數據中[7]可以看到,x從1.67 下降到0.43的范圍內,費米面尺寸(對應于載流子濃度)沒有變化,但是跨過相變點之后費米面消失,體系進入了絕緣態.同時在色散上可以看到(圖5(b)和圖5(c)),準粒子能帶寬度逐步變小,費米速度減小(圖5(d)),到相變之前能帶已經非常窄.這說明準粒子有效質量已很大,最終局域化而進入絕緣態.在這個過程中,相干的準粒子譜權重也是逐步降低的.這些實驗觀察與DMFT 計算[8],或Brinkman-Rice 圖像完全一致[9].

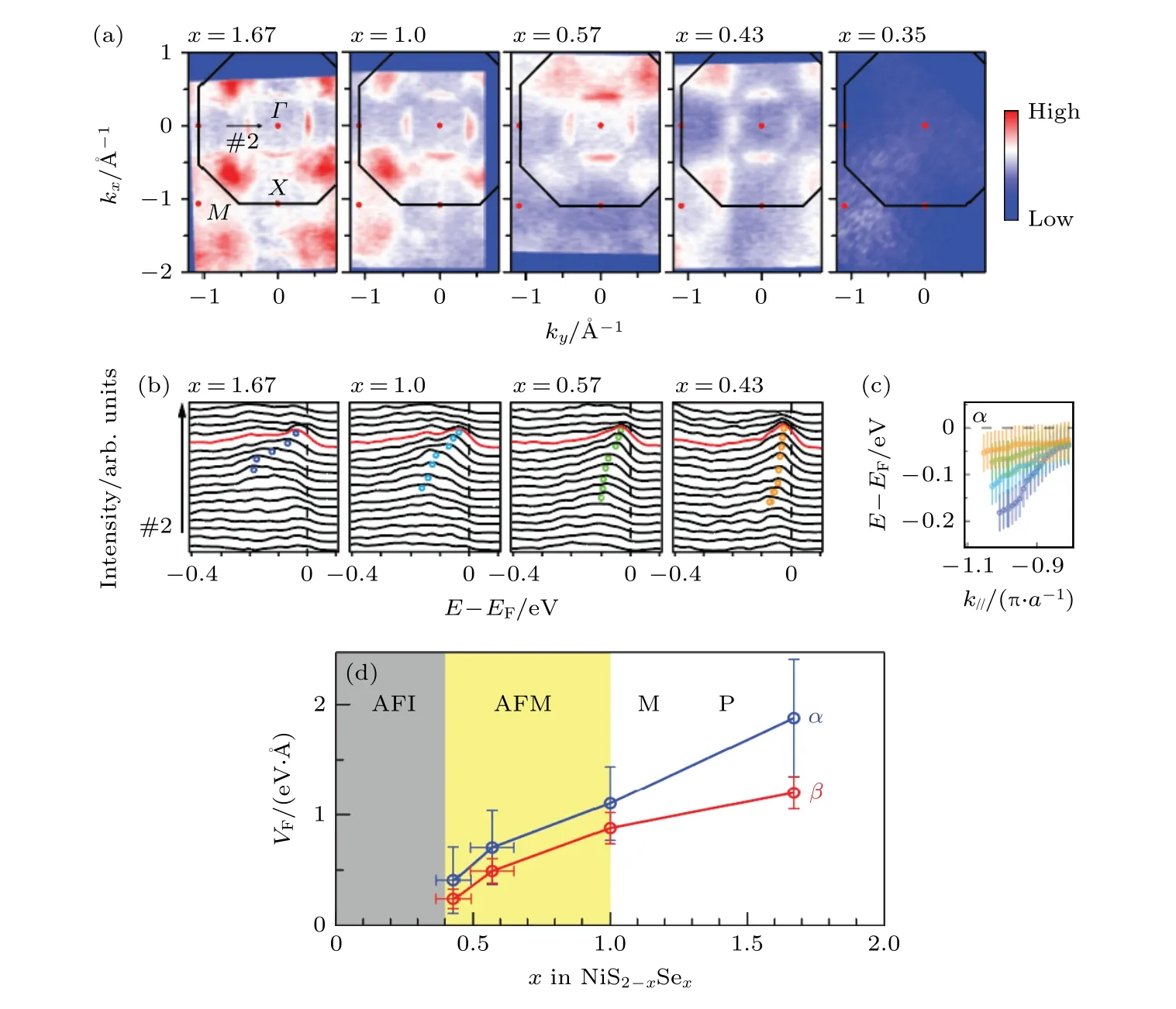
圖5 (a)ARPES 測得NiS2–xSex 的費米面隨著Se 摻雜的演化[7];(b)ARPES 能 譜展示能帶色散隨著Se 摻雜的演化[7];(c)圖(b)中的α 能帶寬度隨摻雜演化的對比[7];(d)NiS2–xSex 兩個能帶的費米速度在摻雜相圖中的演化,在接近莫特絕緣相過程中呈現帶寬變窄、有效質量發散的行為[7]Fig.5.(a)ARPES data of the Fermi surface of NiS2–xSex as Se doping is varied[7];(b)ARPES spectra show that the band dispersion changes with Se doping[7];(c)summary of the band width evolution with doping in figure (b)[7];(d)the evolution of the Fermi velocities of two bands of NiS2–xSex in the phase diagram as a function of doping,showing a narrowing bandwidth and effective mass divergence near the Mott insulating phase [7].

5 帶寬調控的莫特相變示例之二: 鐵基超導

在鐵基超導發現之初,因鐵砷類超導同時具有空穴型和電子型費米面,且母體是反鐵磁的金屬,基于巡游費米面的弱關聯(weak coupling)超導理論一時成為主流,而不是摻雜的莫特絕緣體這樣的局域圖像(也稱為強關聯圖像,strong coupling),鐵基和銅基兩類高溫超導機理似乎迥異[10–12].但是隨著研究的深入,人們發現弱關聯的超導理論無法統一描述鐵基超導體,反而是基于強關聯局域圖像的t-J-J′ 模型可以更好地統一描述各類鐵基超導體[13].這一發現表明銅氧化物高溫超導和鐵基高溫超導兩者的機理事實上異曲同工.

具體來說,弱關聯理論曾把鐵基超導的相圖演化歸結于摻雜改變了費米面,從而改變了費米面間的電子散射和配對行為.但是對FeAs 類的鐵基超導來說,其調控形式很豐富(有電子或空穴異價摻雜引入載流子的,也有調節化學或物理壓力而不引入載流子的),但它們定性的相圖相似[14],并不能單純用改變載流子濃度來解釋(見圖6(a)).通過系統地研究各種摻雜下的不同類型的鐵基超導體系的電子結構的演化,人們發現超導和費米面演化并無直接關聯,而多種摻雜實質上改變的是能帶寬度[15].比如隨著壓力的增加或引入更多電子等,體系的帶寬逐步增加,電子動能增大,關聯逐步減弱,這樣體系的磁性逐步減弱,在關聯適中時進入了超導態,而隨著關聯進一步減弱,超導消失,進入了金屬態.這就把鐵基超導的多個相圖統一到帶寬調控的框架中.

圖6 (a)基于FeAs 面的鐵基超導的相圖示意圖[14];(b)重電子摻雜的多種鐵硒類超導體系符合統一的相圖[16]Fig.6.(a)Schematic phase diagram of FeAs-based superconductor[14];(b)many heavily electron-doped iron-selenide superconductors conform to a unified phase diagram [16].

再拿另一類基于FeSe 面的重電子摻雜的鐵基超導體來說,其可以通過Te,S 等取代Se 來改變化學壓力,從而改變其能帶寬度[16].已知的大多數這類材料都可以被歸納入同一個相圖中(圖6(b)),它和銅氧化物高溫超導的相圖很類似,只不過現在的橫坐標是反映動能的能帶寬度.當帶寬很窄時,關聯很強,其母體也是莫特絕緣體,隨著帶寬增加,逐步進入超導基態、金屬基態.這表明,帶寬調控的莫特物理在這類鐵基超導中依然成立,其超導配對機制可以用強關聯的局域圖像來描述,與銅氧化物高溫超導異曲同工.

6 碳基材料中的帶寬調控與占據調控的莫特相變

雖然很多碳基材料(包括有機材料)不包含具有較為局域的3d 或4f 電子的元素,在格點上的相互作用勢能(如庫侖相互作用能U)也比較小,但因為其分子較大,格點之間波函數交疊程度或電子躍遷的動能t較小,U/t也處于關聯體系的參數區間.因此,碳基材料也可能表現出有趣的關聯行為.

其中一個典型的帶寬調控的例子是A15 結構的Cs3C60(結構如圖7(a)所示,陽離子為堿金屬Cs+,陰離子按照體心立方的結構堆疊),其隨著壓力的相圖如圖7(b)所示.當元胞體積較大,即兩個C60分子距離較遠,帶寬比較窄,該體系處于反鐵磁絕緣體態.而隨著元胞變小,t增大,逐步進入反鐵磁和超導共存態、超導態,隨后超導轉變溫度降低[17].該相圖和上述的銅氧化物超導與鐵基超導相圖有相似之處.

圖7 (a)A15 Cs3C60 (晶體群Pm3n)的晶體結構,其中取向有序的 陰離子按照體心立方的結構堆疊,紅色為Cs+陽離子[17];(b)A15 Cs3C60 加壓后的相圖,顯示了反鐵磁與超導相變溫度隨著富勒烯陰離子體積的演化[17]Fig.7.(a)The crystal structure of A15 Cs3C60 (crystal group Pm3n),where anions with an ordered orientation are stacked in a body centered cubic structure,and Cs+ cations are shown in red[17];(b)the phase diagram of A15 Cs3C60 under pressure shows the evolution of antiferromagnetic and superconducting phase transition temperature with the volume of fullerene anions [17].

當然目前還不能完全確定其超導的機理是來自反鐵漲落還是電聲子相互作用,比如隨著t的增大,態密度減小,基于BCS 電聲子配對機理,也能解釋該相圖中高壓區超導轉變溫度的下降行為.然而BCS 圖像不能解釋在低壓區的行為,隨著元胞變小,理論計算也確認了態密度會減小,但超導卻逐漸出現,并且超導轉變溫度增加,這部分的超導演化不同于BCS 圖像[17].

近年來,人們在轉角雙層石墨烯中也發現了占據調控的莫特物理的相圖(圖8).雖然石墨烯本身U不大,但是轉角后的能帶非常窄[18],U/t處在強關聯的區間,因此隨著通過門電壓調控載流子濃度,觀察到由莫特絕緣體進入超導和金屬態的行為[19].

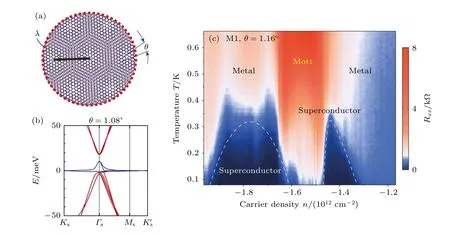
圖8 (a)轉角雙層石墨烯中的莫爾超晶格[18];(b)在轉角為“魔角”(θ=1.08°)時雙層石墨烯的能帶結構,在費米能附近看到平帶(藍色曲線)[18];(c)“魔角”雙層石墨烯中調控電荷濃度得到的相圖,在半填充的莫特絕緣相附近存在兩個超導的拱形區域[19]Fig.8.(a)Moiré superlattice in twisted-angle bilayer graphene[18];(b)the calculated band structure of the twisted bilayer graphene at the magic twisted angle (θ=1.08°),exhibiting a flat band (blue curve)near the Fermi energy[18];(c)the phase diagram of“magic angle”twisted bilayer graphene as a function of charge concentration,there are two superconducting domes near the half-filled Mott insulator phase[19].

7 重費米子體系中的巡游與局域之爭

重費米子體系中的復雜現象常常源于導帶電子在局域自旋晶格的背景下運動.其中的f 電子波函數在高溫下和巡游電子波函數交疊(常被稱為c-f 雜化),但因為其局域性和無序性,這樣的雜化在不同的格點之間沒有相干性.在低溫下,這個過程逐步變得相干,從而f 電子的平帶與巡游電子能帶雜化,使得巡游電子能帶的有效質量越來越大,甚至是幾個量級的提升.f 電子通過這個過程,也參與到費米海中,使得費米面的體積逐步增大,這就是所謂的從小費米面到大費米面的轉化[20].這個過程可以用周期性Anderson 模型來描述,其中的近藤相互作用項(JK)描述了導帶電子與f 電子局域晶格自旋的相互作用.

在CeCoIn5中,人們觀察到了4f 電子隨溫度降低所發生的局域-巡游轉變,即重費米子如何變重的過程.在溫度170 K 時只能觀察到非4f 電子形成的導帶,c-f 雜化的過程在高于100 K 的較高溫度就逐步發生了,到了近藤溫度(～50 K)以下時,局部的c-f 雜化演化成為相干的能帶雜化,可以清晰地觀察到f 能帶及其因為雜化而被彎曲的行為,其能帶的有效質量也以A-BlnT的形式發散,如圖9 所示.值得注意的是,低溫下的費米面確實比高溫時大了,但是在所測量的最低溫度17 K 時,只是部分4f 電子(～5%)參與到了費米面中[21].

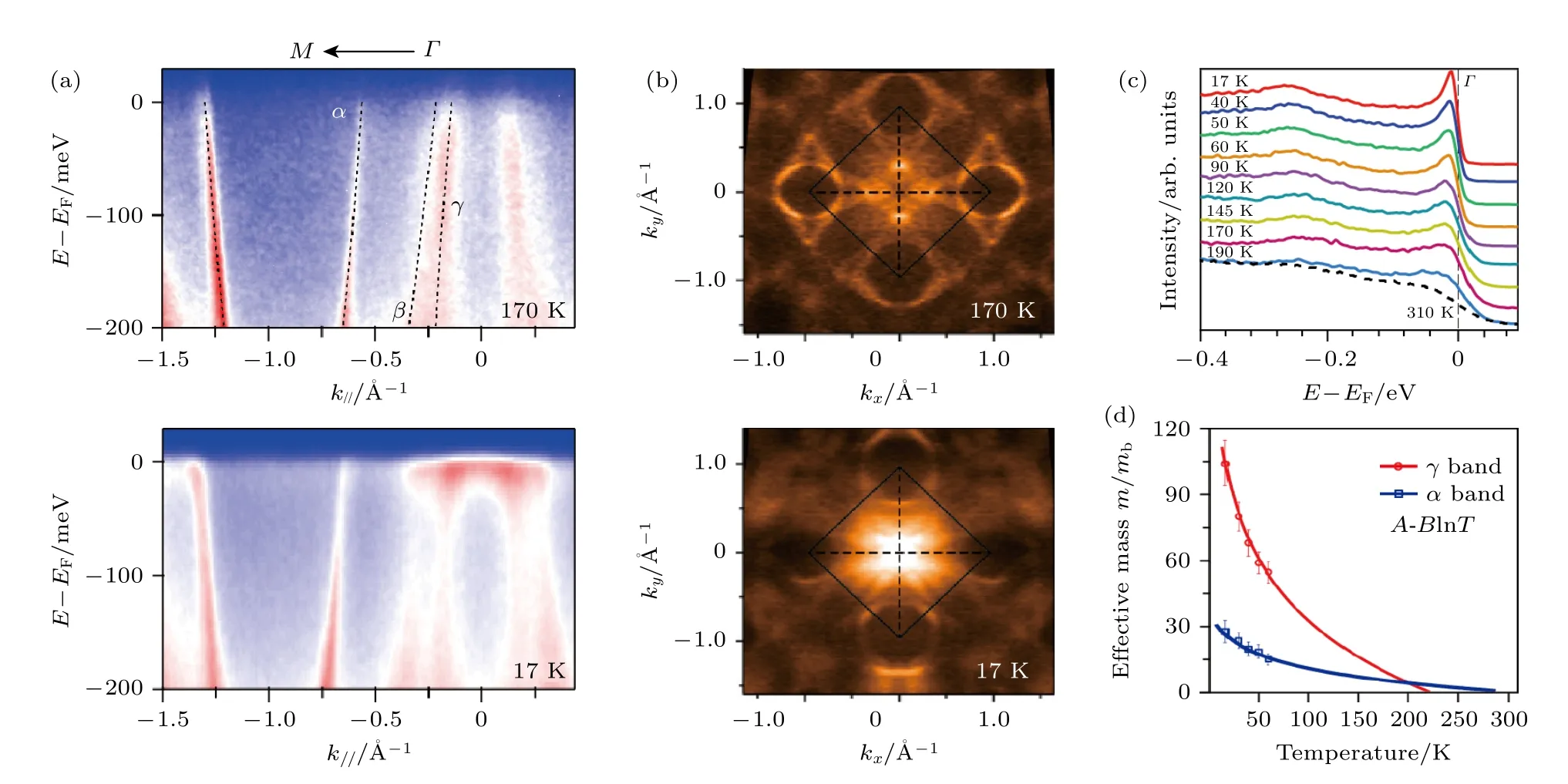
圖9 (a)CeCoIn5 高低溫的能帶結構對比圖,上圖測量溫度為170 K,下圖測量溫度為17 K[21];(b)CeCoIn5 高低溫的費米面對比圖,上圖測量溫度為170 K,下圖測量溫度為17 K[21];(c)CeCoIn5 中Γ 點附近4f 電子譜重隨溫度的演化[21];(d)CeCoIn5 中α 和γ 能帶的有效質量與溫度的依賴關系[21]Fig.9.(a)The band structures of CeCoIn5 at 170 and 17 K,respectively[21];(b)the Fermi surface maps of CeCoIn5 at 170 and 17 K,respectively[21];(c)the evolution of 4f electron spectral weight near the Γ point as a function of temperature in CeCoIn5[21];(d)the effective masses of the α and γ bands of CeCoIn5 as a function of temperature [21].

由于巡游電子的媒介,兩個局域自旋可以發生RKKY(Ruderman-Kittel-Kasuya-Yosida)磁性相互作用,可以導致磁有序.而近藤相互作用則是讓巡游電子屏蔽f 電子的局域磁矩,使得體系進入費米液體或近藤絕緣體等狀態.這兩個效應相互競爭的哈密頓量是

本質也是局域自由度與巡游自由度相互作用,從而產生不同基態,可見于Doniach 相圖(圖10(a))[22].在該相圖中,當JK較小時,TKTRKKY,局域磁矩被屏蔽,體系進入費米液體狀態.而在Jc附近,由于量子臨界現象,有較強的量子漲落,就有可能出現一些新的物態,比如超導態.

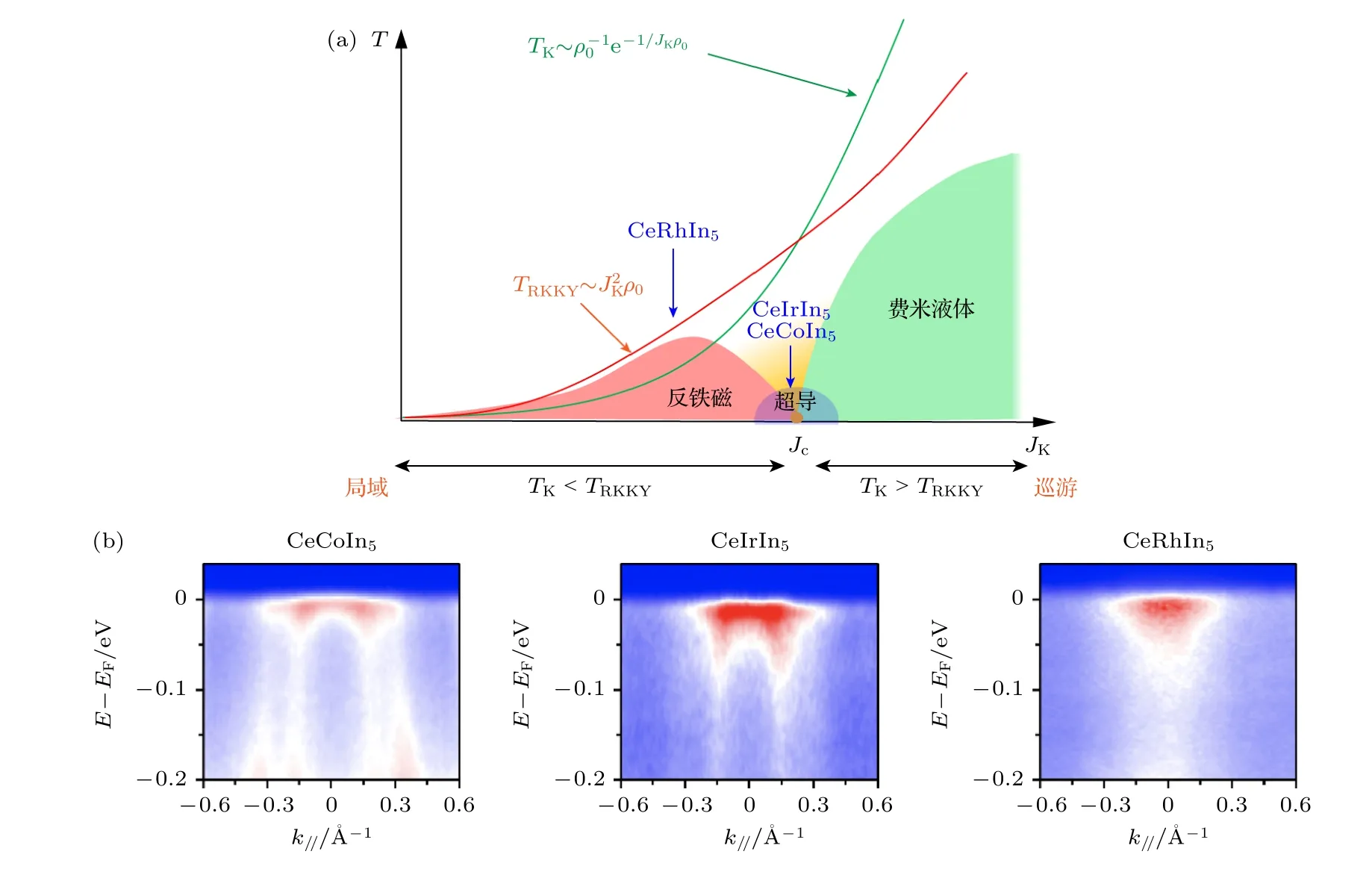
圖10 (a)Doniach 相圖,圖中箭頭標出了CeCoIn5,CeIrIn5 和CeRhIn5 在該相圖中的大致位置[23];(b)CeCoIn5,CeIrIn5 和CeRhIn5中費米能附近能帶雜化行為的對比[23]Fig.10.(a)Doniach phase diagram,with arrows indicating the schematic positions of CeCoIn5,CeIrIn5,and CeRhIn5 in the diagram[23];(b)comparison of the hybridization behavior of the bands near the Fermi energy in CeCoIn5,CeIrIn5,and CeRhIn5 [23].

重費米子體系的基態敏感地依賴于巡游電子與局域自旋的相互作用程度,JK.這與c-f 雜化程度密切相關.比如CeCoIn5,CeRhIn5,CeIrIn5這三個Ce115 家族材料中,CeCoIn5和CeIrIn5的c-f雜化較強,巡游電子屏蔽局域磁矩的效應強,體系表現為費米液體行為和超導基態;而CeRhIn5則是其中c-f 雜化最弱的,基態是反鐵磁的磁有序態,如圖10(b)所示.

另一個典型的例子是方鈷礦結構的4f2近藤晶格體系PrOs4Sb12(POS)和它的4f1兄弟體系CeOs4Sb12(COS).這兩種材料具有相同的晶格常數,相似的導帶費米面,但是在低溫下,COS 中的c-f 雜化過強,打開了雜化能隙,而該體系的化學勢正好在此能隙中,因此COS 成為了近藤絕緣體.而POS的2 個f 電子在有限溫度下,有一定的自旋三態分量,可以被巡游電子屏蔽,具有一定的c-f 雜化[24].在極低溫時,其4f2基態是個自旋單態,不與外界巡游電子發生作用,巡游電子有效質量在極低溫下反而變小,其基態可能是由普通導帶電子引起的超導態.

8 結語

在上述例子中可以看到,大量的關聯體系的基態和演化過程都可以從莫特物理的角度來分析,帶寬調控和占據調控從不同路徑調控了電子動能和勢能的強弱對比,從而使得物態發生了相轉變.巡游與局域之爭是一個根本性的競爭關系,因此在研究關聯體系的過程中需要特別關注.更廣義地來看這個問題,我們可以借助老子的《道德經》第一章來進行一個比擬:

道可道,非常道;(The fundamental laws (or Hamiltonians)are abstract,not easy to describe.)

名可名,非常名;(The manifestations of the laws are everywhere,and very diversified.)

無名天地之始;(The universe starts from the vacuum when nothing has been manifested.)

有名萬物之母.(The manifestations of the laws generate everything in the universe.)

對這四句深奧經文的理解可以有很多種,括號中是我“凝聚態物理版的英文翻譯”,以避開古文的多意和含糊.在凝聚態物理中,“道”是哈密頓量,“名”即是對哈密頓量的表達,在不同材料中的表達給出了千變萬化的量子材料世界.“The manifestation of laws”(道的表達或者“名”)就是“emergence”(演生).凝聚態物理的目標既是要發現新的材料(發現more is different),更是要研究清楚復雜量子材料中的奇妙物性是如何演生出來的(回答how is more different?).在本文上述例子中看到,雖然描述不同關聯體系中的電子巡游性與局域性競爭的哈密頓量很簡單,但是它的表達是很奇妙的,需要抽絲剝繭才能找到萬物背后“名”的過程.

感謝胡江平、閆亞軍、徐海超、陳秋云、彭瑞、沈大偉、張童、杜增義幫助做圖或潤色.