ARIMA 模型在基層血站單采血小板臨床需求量預測中的可行性分析

呂藝通 劉志泉 莫巧頻 王東 謝慶歡 劉曼麗

近年來, 隨著醫療衛生的改革, 順德地區多家三甲、二甲醫院由國內知名醫科大學托管, 醫院診療水平顯著提升, 臨床用血量也逐年上升。順德區中心血站作為轄區內唯一的采供血機構, 承擔著全區的采供血任務, 年采供血量達13 噸。作為一個基層中心血站, 其轄區面積、常住人口數量、人力物力的投入以及對血液應急調配的權限和靈活度都不如市級中心血站及血液中心。因此, 如何精準把控血液庫存, 既要滿足臨床的用血需求, 又要避免因血液庫存過高而過期報廢, 是基層血站庫存管理工作需要考慮的重要問題之一。血小板作為挽救患者的重要血液成分, 被廣泛應用于血小板數量減少或功能障礙等引起的出血患者的輸血治療［1］。因其采集方式特殊, 保存時間特別短,保存期僅為5 d, 不宜大量貯存, 采供矛盾最為突出, 所以對如何科學合理地規劃庫存提出了更高的要求, 是一個值得深入研究的課題。ARIMA 模型是一種被廣泛應用的數學模型, 通過分析時間序列前后數據的相關性, 利用歷史數據的規律預測疾病發生的趨勢［2］。本研究擬運用ARIMA 模型對順德區中心血站2012 年1 月～2022 年6 月的單采血小板臨床使用量進行分析并建立模型, 并用于預測2022 年7 月～2023 年3 月臨床單采血小板需求量, 為順德區中心血站單采血小板的招募采集、制定合理的血小板庫存提供科學依據,現報告如下。

1 材料與方法

1.1 數據來源 通過SHINOW9.5 現代血站管理信息系統, 獲取順德區中心血站2012 年1 月～2022 年6 月的單采血小板使用量數據(因本研究時間段內, 順德區中心血站所制備的濃縮血小板量極少, 所以不納入本次研究對象)。臨床單采血小板使用量以治療量計算［3］,1 個治療量血小板計數≥2.5×1011/L。

1.2 建立ARIMA 模型 建立ARIMA 模型的步驟：①原始時間序列及平穩化處理。繪制2012 年1 月～2022 年6 月順德區中心站單采血小板臨床使用量的原始時間序列圖, 分析原始序列圖是否為具有趨勢和季節性趨勢的不平穩序列, 對不平穩序列進行差分, 使序列平穩化。②ARIMA 模型識別和參數估計。根據ACF 圖和PACF 圖的特征, 以及是否出現拖尾或截尾的情況來推斷出p、d、q 值, 并初步建立若干個備選的ARIMA 模型, 如果時間序列有明顯的趨勢和季節性趨勢, 應選擇建立ARIMA(p, d, q)(P, D, Q)s 乘積季節性模型, 其中p、q 分別為非季節自回歸和移動平均的階數, P、Q 分別為季節性自回歸和移動平均的階數, d、D 分別為差分和季節性差分的次數, s 為循環的季節周期［4］。對備選模型參數P 值進行檢驗, 若P＜0.05, 則差異有統計學意義, 參數檢驗通過。根據時間序列的識別規則, 結合ACF 圖、PACF 圖和貝葉斯準則(BIC準則), 對各個模型的標準化BIC 值的大小進行比較,BIC 值越小的模型, 擬合效果越好［5,6］, 從而選出最優模型。③ARIMA 模型檢驗。根據殘差序列的自相關圖、偏相關圖和殘差序列Ljung-Box Q 的統計結果判斷殘差是否存在自相關性, 若P＞0.05, 則殘差通過白噪聲顯著性檢驗, 所建模型擬合效果較好。④模型預測。利用建立的最優模型, 預測2022 年7 月～2023 年3 月順德區臨床單采血小板的使用量, 并與實際使用量進行比較, 計算平均相對誤差, 以驗證模型的擬合效果。

1.3 統計學方法 應用SPSS23.0 統計學軟件對單采血小板臨床使用量進行數據錄入, 并對數據進行統計分析, 建立ARIMA 模型。對確立的模型進行白噪聲檢驗, P＜0.05 為差異有統計學意義。

2 結果

2.1 原始時間序列分析及平穩化處理 通過繪制順德區中心血站2012 年1 月～2022 年6 月單采血小板臨床使用量的原始序列圖(見圖1), 由原始序列圖可見, 單采血小板臨床使用量呈逐年上升趨勢, 而且序列圖存在明顯的季節性周期波動, 以12 個月為1 個周期, 每年的1、2 月份單采血小板使用量最低, 每年的7、8、11、12 月份使用量最高。原始序列圖不平穩, 因此,對數據進行1 階差分和1 階季節性差分, 差分后的序列圖圍繞0 值上下波動, 為平穩序列(見圖2)。

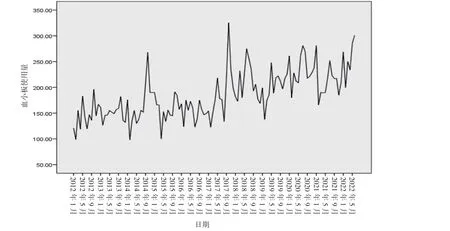
圖1 單采血小板臨床使用量的原始序列圖

2.2 模型的識別和參數估計 因2012 年1 月～2022 年6 月單采血小板臨床使用量呈逐年上升趨勢, 而且序列圖存在明顯的季節性周期波動, 所以選用ARIMA(p, d, q)(P, D, Q)s 乘積季節性模型, 由2.1 分析可知,季節性周期為12 個月, 故s=12, 對數據進行平穩化處理時, 分別進行了1 階差分和1 階季節性差分。因此, d=1, D=1。通過分析差分后的ACF 圖(見圖3)和PACF 圖(見 圖4)可 知, ACF 圖 在 滯 后1, 2, 5, 7, 12,13 階時均有突起, 拖尾和截尾特征不明顯, 故q=0；PACF 圖在滯后1, 2 階突起, 第2 階后明顯回縮, 呈2 階截尾, 故p=2。另外, ACF 圖在滯后12 階時顯著不為0, 故Q=1；PACF 圖在滯后12 階附近顯著不為0,故P=0 或1。因此, 初步識別的模型為ARIMA(2, 1, 0)(0, 1, 1)12和ARIMA(2, 1, 0)(1, 1, 1)12。對所識別的模型進行參數估計和參數檢驗(見表1), 由表1 可知, 模型ARIMA(2, 1, 0)(0, 1, 1)12的BIC 值 小 于 模 型ARIMA(2, 1, 0)(1, 1, 1)12的BIC 值, 且模型參數差異有統計學意義(P＜0.05), 因此, 確定模型ARIMA(2, 1, 0)(0, 1, 1)12為最優模型。

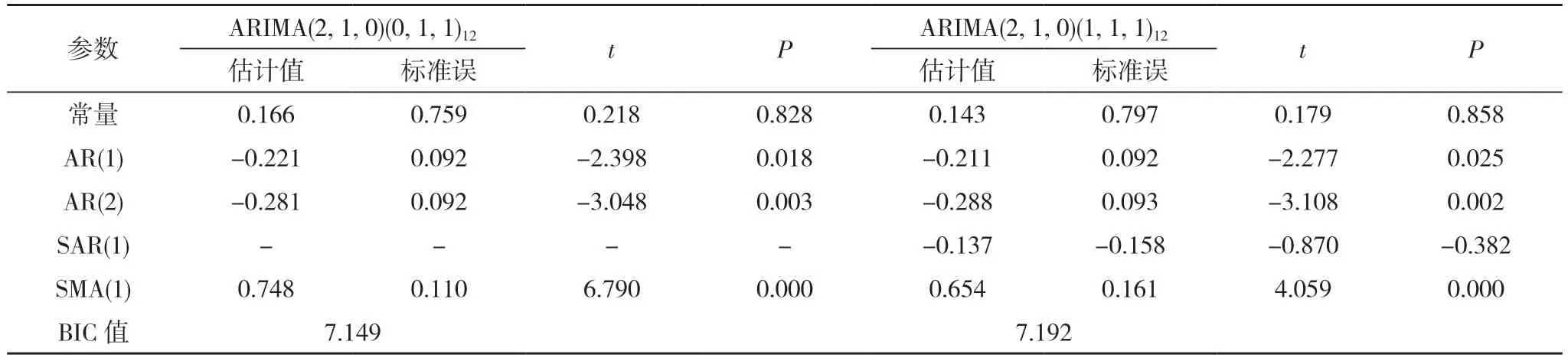
表1 單采血小板臨床使用量識別模型的參數估計和參數檢驗

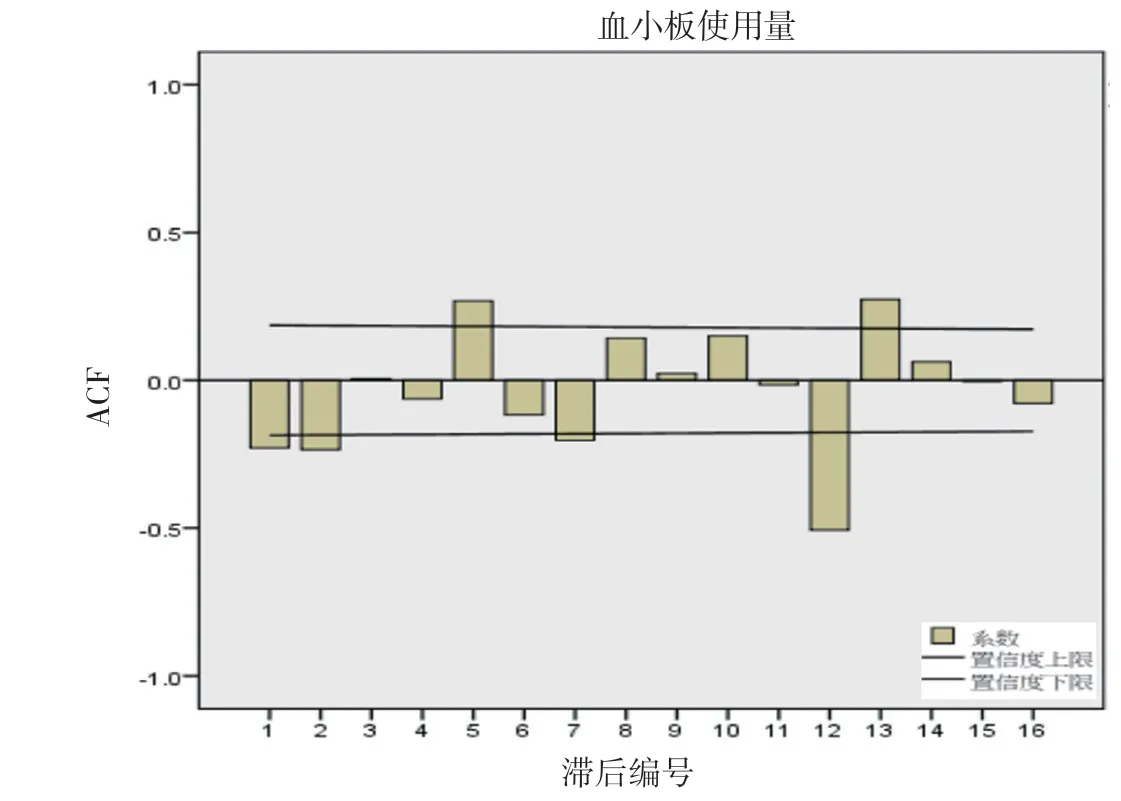
圖3 單采血小板臨床使用量經1 階差分和1 階季節差分后ACF 圖

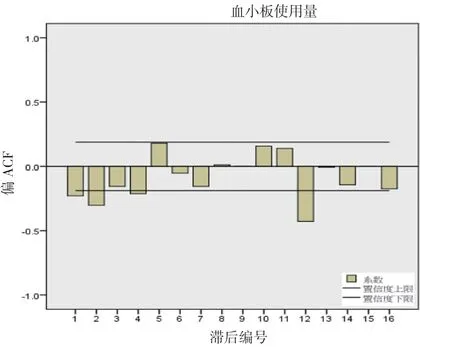
圖4 單采血小板臨床使用量經1 階差分和1 階季節差分后PACF 圖

2.3 模型檢驗 對最優模型ARIMA(2, 1, 0)(0, 1, 1)12殘差序列進行白噪聲檢驗(見圖5), 結果可見殘差序列ACF 和PACF 落 在95%CI 內；Ljung-BoxQ 統 計 量 為24.941, 差異無統計學意義(P＞0.05), 說明殘差是隨機分布的, 殘差不存在相關性, 為白噪聲序列, 模型檢驗通過, 適合用于單采血小板使用量的預測。

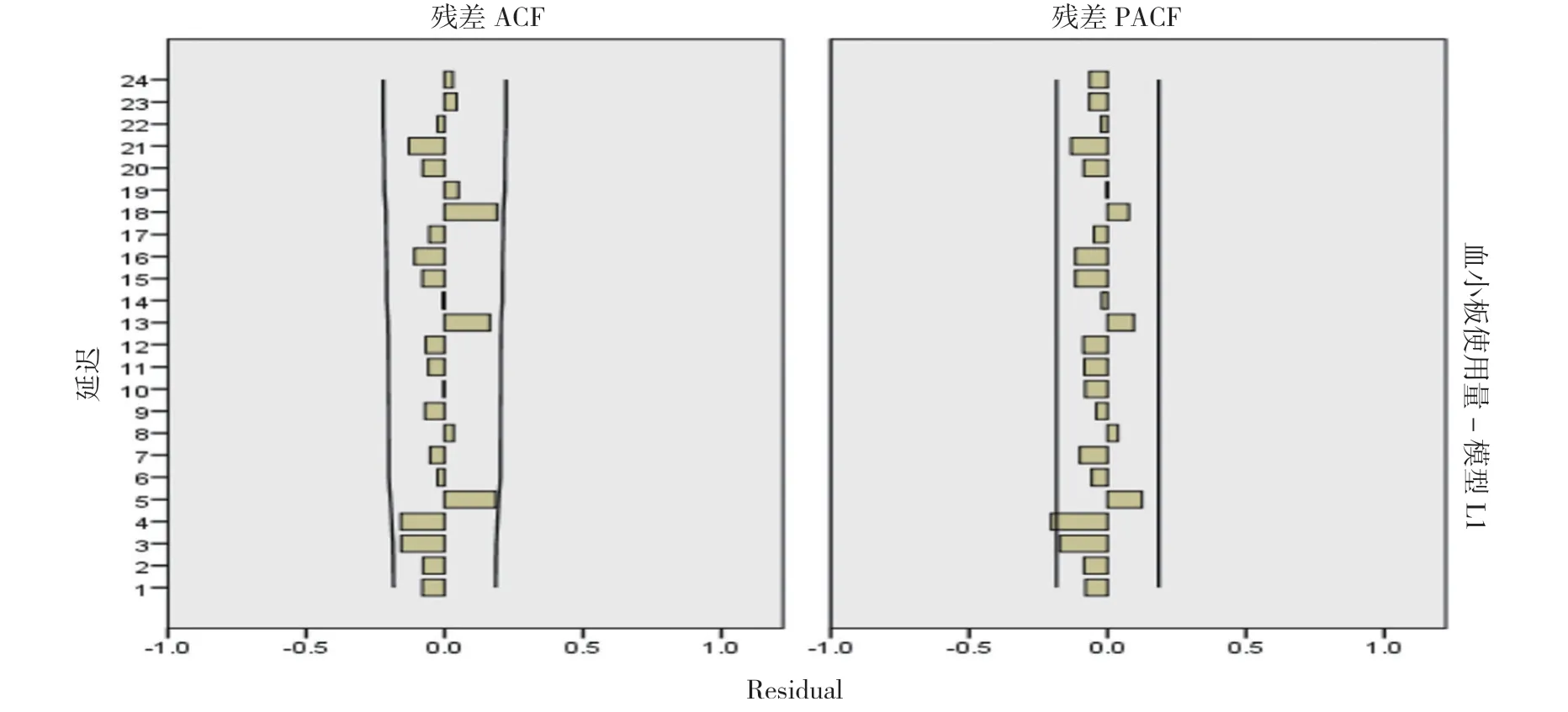
圖5 模型ARIMA(2, 1, 0)(0, 1, 1)12 殘差序列ACF 和PACF 圖

2.4 模型預測 應用模型ARIMA(2, 1, 0)(0, 1, 1)12對順德區2022 年7 月～2023 年3 月的單采血小板臨床使用量進行預測, 預測結果與實際值均在95%CI 范圍內, 平均相對誤差為7.06%(見表2)。由2012 年1 月～2022 年6 月的模型擬合圖可知, 預測值與實際值的曲線趨勢擬合程度較高(見圖6)。大量研究顯示［7-9］, 平均相對誤差＜10%, 則說明所建模型擬合效果較好, 精確度較高。

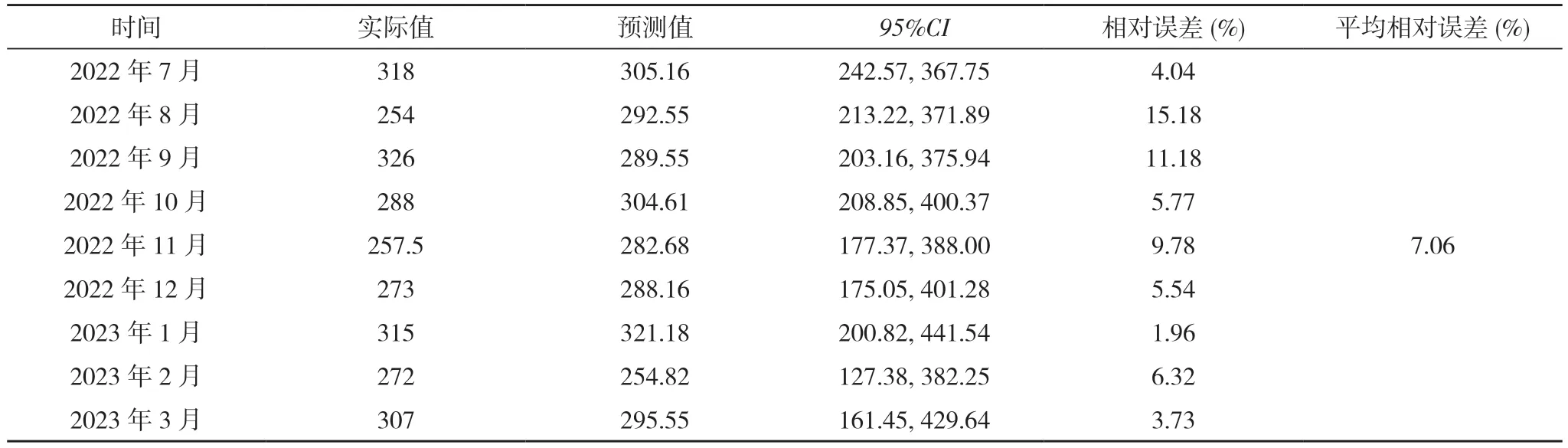
表2 2022 年7 月～2023 年3 月單采血小板臨床實際使用量與預測量比較(治療量)

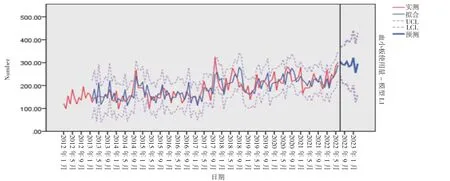
圖6 單采血小板臨床使用量ARIMA(2, 1, 0)(0, 1, 1)12 模型擬合效果圖

3 討論

ARIMA 模型通過對具有趨勢和季節性趨勢的時間序列進行建模, 對每個季節周期中同時間點的序列值進行分析, 提取季節趨勢, 并對每個季節周期內部序列值的變化提取非季節性成分來做預測［10］。它充分考慮了時間序列上的依存關系和隨機波動造成的干擾, 具有建模相對簡單、短期預測精度較高、經濟實用等優點, 目前已被廣泛應用于衛生領域的病毒疫情發展趨勢［11］、疾病發展情況［12,13］、臨床用血趨勢［14］等的預測。有研究顯示［15］, ARIMA 模型在預測臨床用血需求的精確性優于其他時間序列模型。

盡管目前國內已經有不少學者運用不同的數學模型對臨床用血量進行預測［16,17］, 但大部分都是基于省級血液中心和市級中心血站的歷史用血數據而進行的預測, 而對縣、區級血站的相關研究報道甚少, 對基層血站的臨床用血預測缺乏參考依據。本研究通過按月份對順德區中心血站2012 年1 月～2022 年6 月的單采血小板使用量進行統計分析, 并運用ARIMA 時間序列模型進行建模, 經過參數檢驗和BIC 準則對初步確定的模型進行檢驗, 最終確定模型ARIMA(2, 1, 0)(0, 1, 1)12為最優模型。運用最優模型對順德區中心血站2022 年7 月～2023 年3 月的單采血小板臨床使用量進行預測, 結果顯示預測值與實際值的曲線趨勢基本一致, 預測結果值與實際值均在95%CI 范圍內, 平均相對誤差為7.06%, 說明預測效果較精確, 預測效果好。所建模型適合用于順德區的臨床血小板需求量預測。

目前, 順德區中心血站的單采血小板供應方式有兩種：①對于常規患者, 醫院提前預約下單, 獻血科招募采集, 檢測合格后發放給臨床。②對于危急患者, 醫院電話向血站提出緊急用血申請, 血站評估通過后, 發放應急庫存。但在實際工作中, 由于臨床血小板的需求難以估計, 當血小板需求劇增時, 會導致預約的單采血小板供應延遲和應急庫存貯備不足等情況的發生。通過利用ARIMA 模型提前預測每個月的血小板需求量, 獻血服務科可根據預測結果, 有效規劃獻血者的招募和保留工作, 提高招募效率, 供血服務科可根據預測結果, 合理地制定動態的單采血小板應急庫存和對臨床醫院采取必要的用血管理措施, 在一定程度上彌補了基層血站依靠工作經驗來預測庫存的不足, 有利于維持單采血小板的采供平衡, 既保證了臨床用血, 也避免了血液的過期報廢。但該模型也有一定局限性, 研究顯示, 該模型是通過歷史數據的慣性趨勢而建立的,忽略了國家的重大政策調整和突發事件等外在因素,只適用于短期預測［18］。因此, 在今后的研究工作中,需要不斷更新數據, 及時對模型進行修正和調整, 以提高預測結果和實際結果的擬合精確度。