制動工況下風(fēng)電偏航摩擦片聲學(xué)特性研究

候 建，李麗霞，張 毅，王其良，王建梅，2

(1.太原科技大學(xué) 重型機(jī)械教育部工程研究中心，山西 太原 030024；2.山西工程技術(shù)學(xué)院，山西 陽泉 045000)

0 前言

隨著我國經(jīng)濟(jì)的發(fā)展和科技的進(jìn)步，風(fēng)能、氫能和太陽能等清潔能源已成為未來發(fā)展趨勢。發(fā)展風(fēng)電技術(shù)對于國家調(diào)整能源結(jié)構(gòu)、應(yīng)對氣候變化、實(shí)現(xiàn)“雙碳”戰(zhàn)略具有重要意義。偏航制動器作為大型風(fēng)力發(fā)電機(jī)組上的重要設(shè)備，可以實(shí)現(xiàn)風(fēng)電機(jī)組精準(zhǔn)對風(fēng)，保障風(fēng)力發(fā)電效率，是機(jī)組高效平穩(wěn)運(yùn)行的關(guān)鍵組成部分。

迄今為止，國內(nèi)外學(xué)者已經(jīng)對盤式制動器做了大量研究。Ahn S等[1]通過改造盤式剎車片的形狀以減小摩擦界面的不均勻接觸，利用有限元模型得到了接觸應(yīng)力的分布，并通過現(xiàn)場試驗(yàn)得以驗(yàn)證。劉旭[2]對簡化的制動系統(tǒng)進(jìn)行應(yīng)力分布分析，得到了最大應(yīng)力的位置。王岳峰等[3]建立了偏航制動器的熱力耦合有限元模型，得到了偏航壓力、偏航速度、摩擦系數(shù)等因素對熱應(yīng)力的影響。CH-Yoo等[4]利用杠桿原理設(shè)計(jì)了一種檢測偏航制動扭矩的裝置，并通過實(shí)驗(yàn)驗(yàn)證了裝置的可行性。徐曉光[5]利用摩擦磨損實(shí)驗(yàn)探究了不同含量珠光體對風(fēng)機(jī)制動性能的影響，結(jié)果表明珠光體含量越高，摩擦片的摩擦性能越高。Miranda M H P等[6]針對摩托車盤式制動器尖叫問題，建立了制動器有限元模型，并探究了材料參數(shù)和操作參數(shù)對噪聲產(chǎn)生的影響。S. W. Kung等[7]對制動器各部件進(jìn)行自由模態(tài)求解，結(jié)果發(fā)現(xiàn)制動塊是影響制動器穩(wěn)定性最大的部件。潘公宇等[8]利用三維掃描技術(shù)和SOLIDWORKS對制動器建模，通過優(yōu)化剎車片中的粘彈性成分來實(shí)現(xiàn)降噪，并以Dyno臺架試驗(yàn)驗(yàn)證了仿真結(jié)果。A. Bajer等[9]通過對摩擦阻尼的研究發(fā)現(xiàn)，忽略摩擦阻尼的不穩(wěn)定模態(tài)大于實(shí)際情況下的不穩(wěn)定模態(tài)。常慶斌等[10]通過采用活塞偏心布置及加強(qiáng)卡鉗支架的方式，改善摩擦片偏磨導(dǎo)致的制動低鳴噪聲問題。管迪華等[11]采用能量饋入法對制動盤和摩擦片的接觸制動噪聲進(jìn)行了研究，通過改變摩擦片的倒角、摩擦因數(shù)或材料參數(shù)等對抑制制動噪聲均起到有效的作用。吳奕東等[12]采用能量饋入法對非對稱制動壓力下的制動器開展研究，發(fā)現(xiàn)通過提高制動壓力的對稱性可以提高復(fù)特征頻率，從而使低頻制動尖叫難以激發(fā)。呂輝等[13]引入隨機(jī)區(qū)間和區(qū)間不確定參數(shù)對制動器的振動穩(wěn)定性進(jìn)行研究，甄別了不確定性參數(shù)對系統(tǒng)穩(wěn)定性的影響，從可靠性角度提出改善穩(wěn)定性的措施。

目前研究人員對于高速制動工況研究較多，但對低速重載工況下的制動過程和偏航制動器的噪聲研究較少。偏航制動系統(tǒng)在低速重載工況下運(yùn)行時制動器結(jié)構(gòu)會產(chǎn)生振動，嚴(yán)重時會導(dǎo)致其他部件產(chǎn)生共振，影響制動器的壽命，極大增加了偏航制動系統(tǒng)的維修成本，同時摩擦系統(tǒng)的尖叫問題還會造成噪音污染影響居民的生活。因此，分析偏航系統(tǒng)的振動噪音問題對于風(fēng)電機(jī)組的運(yùn)行具有重要意義。

1 風(fēng)力發(fā)電機(jī)偏航制動器模型

1.1 偏航制動器有限元模型

風(fēng)力發(fā)電機(jī)的偏航制動系統(tǒng)是機(jī)組關(guān)鍵組成部分，如圖1所示[14]，其功能是確保風(fēng)機(jī)的精準(zhǔn)對風(fēng)，避免風(fēng)能損失。偏航制動性能的好壞決定了偏航系統(tǒng)的穩(wěn)定性和整個風(fēng)電機(jī)組運(yùn)行的安全性。由于制動器噪聲問題復(fù)雜，本文以制動器的關(guān)鍵部件作為研究對象，根據(jù)偏航制動器實(shí)際尺寸創(chuàng)建三維幾何模型，利用有限元法進(jìn)行聲學(xué)模擬。

圖1 偏航系統(tǒng)結(jié)構(gòu)圖[14]

1.2 偏航制動系統(tǒng)的運(yùn)行工況與材料參數(shù)

根據(jù)文獻(xiàn)[15]中偏航制動器的運(yùn)行工況，得到偏航壓力、偏航速度和摩擦系數(shù)的取值范圍，將文獻(xiàn)中的參數(shù)作為模擬中偏航制動器的運(yùn)行工況，如表1所示。制動盤的材料為Q345E，摩擦片的材料為復(fù)合樹脂基，兩者的材料參數(shù)如表2所示。

表1 制動器運(yùn)行工況

表2 摩擦副材料性能參數(shù)

1.3 制動器空氣域模型

在對偏航制動器進(jìn)行動力學(xué)模擬后，為了模擬周圍的輻射噪聲，需要在偏航制動器外部提前創(chuàng)建一個空氣域。為了簡化計(jì)算量，空氣域模型要盡可能地小，如圖2所示。在耦合動力學(xué)與聲學(xué)時，假設(shè)單項(xiàng)耦合，即偏航制動器的振動會影響周圍的空氣，但忽略聲波對結(jié)構(gòu)本身的影響。聲學(xué)域的作用是將動力學(xué)參數(shù)映射到聲學(xué)域的內(nèi)部邊界網(wǎng)格上，對聲學(xué)域進(jìn)行無反射全吸收處理，進(jìn)而獲得不同頻率下近聲場的輻射聲壓級。為了了解噪聲輻射特性，設(shè)置場點(diǎn)獲得遠(yuǎn)處聲場的輻射圖。

圖2 偏航制動器空氣域模型

2 聲學(xué)方程與聲學(xué)邊界條件

2.1 聲學(xué)基本方程

基于聲學(xué)理論，聲學(xué)方程的任何一種形式都可以從流體的連續(xù)方程、物態(tài)方程、運(yùn)動方程、能量方程推導(dǎo)而來，對方程作不同的假設(shè)，可以得到不同的聲學(xué)方程。基于運(yùn)動介質(zhì)聲學(xué)的基本方程，假定定常流動下的流體密度、速度、壓力、熵均為常數(shù)，外部作用于流體的力為零，得到均勻流中傳播的基本聲學(xué)方程[16]：

(1)

式中，ρ0為定常流動下流體的密度；c0為定常流動下的聲速；q為流體質(zhì)量源；t為時間；p為流體壓力；p0為定常流動下的流體壓力。

根據(jù)傅里葉變化求解聲學(xué)頻域形式下的聲學(xué)基本方程：

(2)

式中，k為波數(shù)，k=w/c=2πf/c；w為角頻率；f為頻率，對應(yīng)的波長λ=2/k=2πc/w=c/f。

2.2 邊界條件

在求解聲學(xué)問題中，為了解決結(jié)構(gòu)網(wǎng)格和聲學(xué)網(wǎng)格不匹配的問題，將結(jié)構(gòu)網(wǎng)格上的參數(shù)映射到聲學(xué)邊界網(wǎng)格上，通過定義聲學(xué)邊界條件，求解得到聲學(xué)方程的唯一解。本文采用的位移邊界條件是速度邊界的變形。基本聲學(xué)邊界條件為以下三種[17]：

(1)聲質(zhì)點(diǎn)速度邊界

聲質(zhì)點(diǎn)速度邊界的形式為

(3)

(2)聲壓邊界條件

聲壓邊界條件形式為

(4)

(3)阻抗邊界條件

阻抗邊界條件形式為

Ap=Bvn=C

(5)

式中，A、B、C為已知值，阻抗邊界條件是通過對聲壓和聲質(zhì)點(diǎn)速度的關(guān)系來約束邊界條件，阻抗邊界條件的物理意義是聲學(xué)邊界網(wǎng)格的吸聲系數(shù)或反射系數(shù)。

2.3 聲學(xué)輻射模型

偏航制動盤與摩擦片在制動過程中使得制動系統(tǒng)產(chǎn)生劇烈振動，導(dǎo)致偏航制動器發(fā)出噪音。聲學(xué)有限元法仿真是將制動器的結(jié)構(gòu)彈性域和噪聲輻射的流體域離散，再通過聲學(xué)波動方程和力學(xué)方程求解得到結(jié)果。為了揭示制動盤和摩擦片的聲場分布規(guī)律，文中采用聲學(xué)有限元法建立偏航制動器的聲學(xué)輻射模型。聲學(xué)求解的系統(tǒng)方程[17]為

(6)

式中，Ka為聲學(xué)剛度矩陣；Ca為聲學(xué)阻尼矩陣；Ma聲學(xué)質(zhì)量矩陣；pi為節(jié)點(diǎn)聲壓；Qi為聲源向量；Vni為輸入速度向量；Pi為輸入聲壓向量；Fai為聲學(xué)激勵；ω為角頻率。

本文中的聲學(xué)輻射仿真方法采用有限元法，輻射邊界條件采用AML技術(shù)。AML技術(shù)是自動在聲學(xué)輻射邊界設(shè)置一層網(wǎng)格吸收聲學(xué)量，從而確定方程組唯一解。

2.4 聲的合成

噪聲通常包含多種聲源輻射聲音的合成，或者一個聲源包含不同的頻率。為了方便對噪聲進(jìn)行評估，故將噪聲進(jìn)行合成，計(jì)算總聲壓級。一般噪聲均為不相干波，適用于能量相加法，該方法是當(dāng)兩個計(jì)權(quán)后的聲壓級相互疊加時，其總聲壓級由較大的那個聲級決定，因此總聲壓級可由式(7)確定：

(7)

式中，L總為疊加后的總聲壓級；Li為各個獨(dú)立的噪聲源或者各頻帶上的聲壓級。

2.5 制動器不穩(wěn)定頻率

為了確定聲學(xué)仿真中偏航制動器的聲學(xué)求解頻率范圍，采用復(fù)模態(tài)法求解偏航制動器的不穩(wěn)定模態(tài)，根據(jù)不穩(wěn)定模態(tài)的頻率范圍確定聲學(xué)求解的最大頻率。制動器不穩(wěn)定模態(tài)分布如圖3所示，從圖3看出，不穩(wěn)定模態(tài)集中在3～6 kHz，在該階段的正實(shí)部較大，系統(tǒng)最不穩(wěn)定，尖叫發(fā)生的概率較大，噪聲的強(qiáng)度較大[18]，故選取6 kHz為聲學(xué)仿真最大頻率。

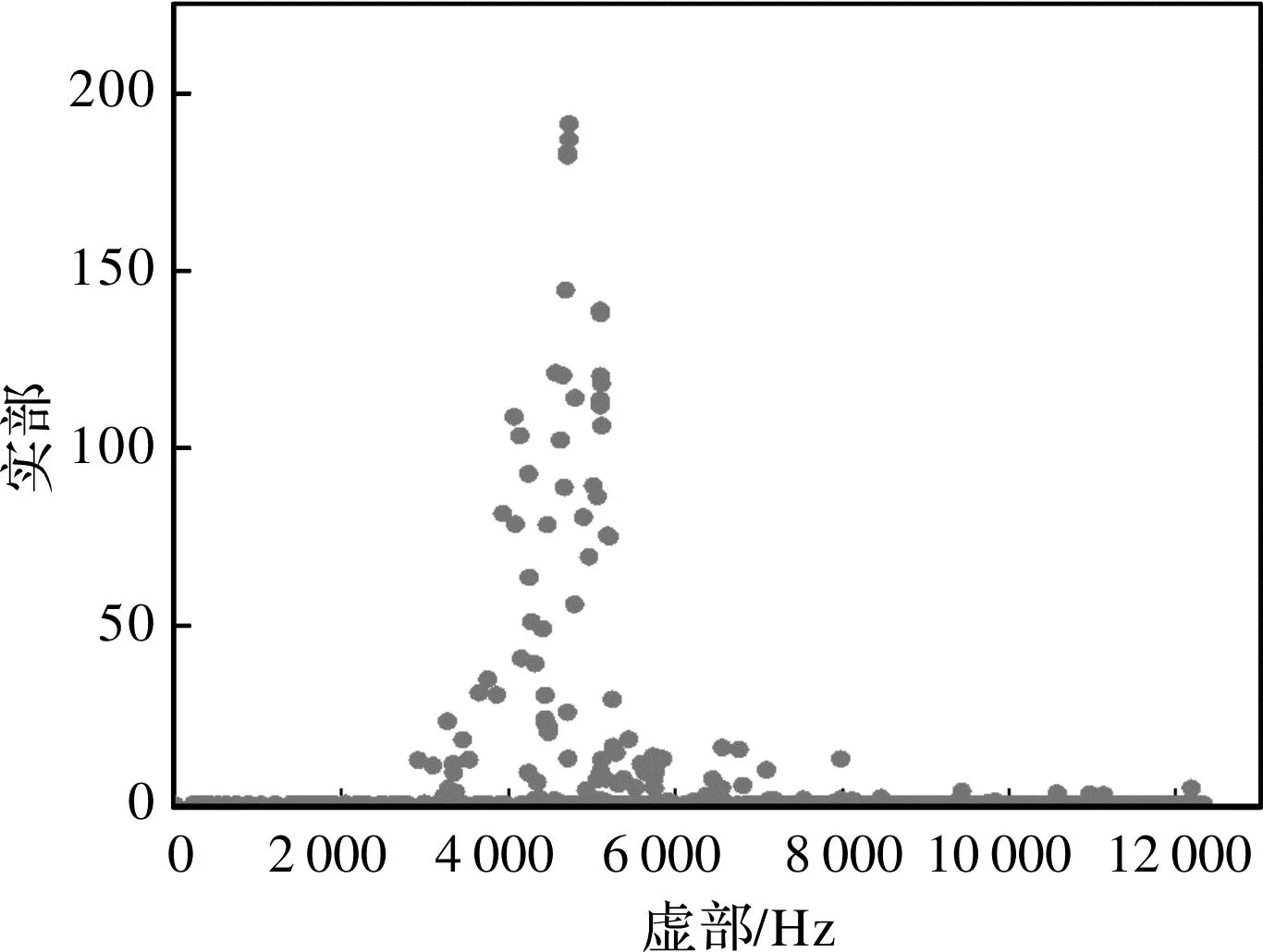
圖3 偏航制動器不穩(wěn)定模態(tài)分布

3 正交試驗(yàn)設(shè)計(jì)

正交試驗(yàn)是根據(jù)Galois理論從全面試驗(yàn)中選出部分具有代表性的水平組合進(jìn)行試驗(yàn)的設(shè)計(jì)方法，它能夠簡化試驗(yàn)，找出最優(yōu)的水平組合。為了分析不同偏航壓力、偏航速度、摩擦系數(shù)下對制動系統(tǒng)聲壓的影響，通過設(shè)計(jì)正交試驗(yàn)法得到不同工況下系統(tǒng)的總聲壓級。根據(jù)表2中的工況并結(jié)合常用正交表，選取L933正交表設(shè)計(jì)正交試驗(yàn)，如表3所示。

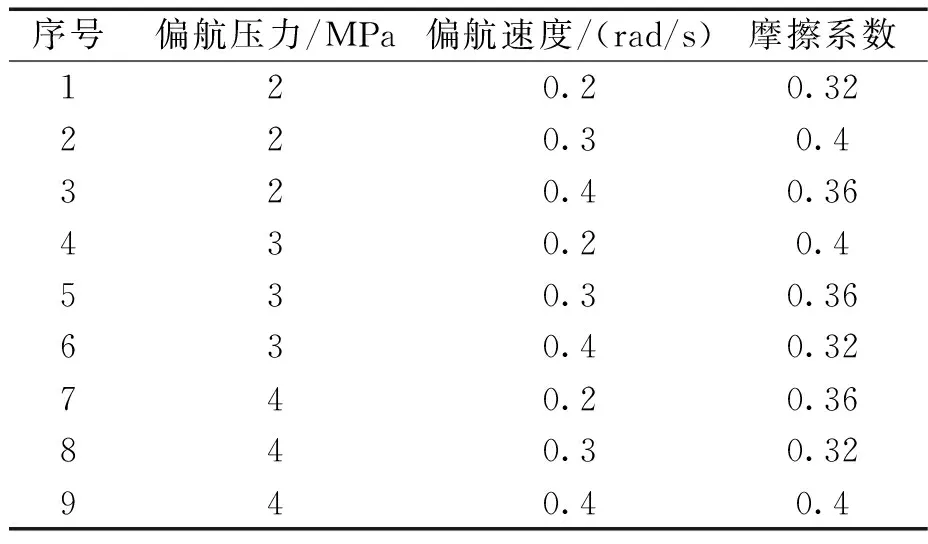
表3 正交試驗(yàn)表

4 計(jì)算結(jié)果討論與分析

4.1 聲場分布規(guī)律

為了研究聲輻射的分布規(guī)律，在聲學(xué)網(wǎng)格上設(shè)置場點(diǎn)，以制動盤中心為原點(diǎn)在水平的正方向上由中心向外分別設(shè)置10個點(diǎn)，在垂直方向的負(fù)方向上(風(fēng)力發(fā)電機(jī)的下方)也設(shè)置10個點(diǎn)。

圖4為p=4 MPa、v=0.30 rad/s、μ=0.32時各方向上的總聲壓變化曲線。

圖4 偏航制動器總聲壓變化圖

從圖4(a)可以看出，豎直方向的總聲壓變化相對于水平方向的變化小，豎直方向整體的聲壓比水平方向的聲壓大，這是因?yàn)樵谀Σ林苿舆^程中垂直方向上的振動相比水平方向上劇烈。

圖4(b)表明制動器的中心位置的聲壓能量最集中且聲壓呈對稱分布，最大聲壓為203 dB，輻射聲壓在垂直方向由制動器中心位置向四周輻射，水平方向聲壓成環(huán)狀梯度分布并逐漸減小。因此需要加強(qiáng)垂直方向的聲壓降噪。

為了分析偏航制動器近場的聲壓在頻率上的變化，選取制動器附近的一點(diǎn)(距制動器中心2 m處)進(jìn)行頻域分析。從圖5近場聲壓分布來看，聲壓最大處在1 375 Hz和2 500 Hz附近，最大聲壓為168 dB，根據(jù)噪聲的頻率分類劃分標(biāo)準(zhǔn)，該頻率范圍的噪音屬于低頻尖叫噪聲，低頻尖叫的發(fā)生是由于制動系統(tǒng)的動態(tài)失穩(wěn)造成，與系統(tǒng)的模態(tài)耦合有關(guān)；頻率在3 kHz以上時由于振動能量相比垂直方向的小，水平方向聲壓衰減速度較快；在3～5 kHz之間，聲壓存在多個高峰，這與復(fù)模態(tài)仿真中的不穩(wěn)定模態(tài)的集中頻率區(qū)間相同。

圖5 各方向上頻域的聲壓分布

4.2 偏航速度對偏航制動器聲壓的影響

圖6為p=2 MPa、μ=0.4時，偏航摩擦片在不同偏航速度下的總聲壓變化曲線。由圖6可知，隨著偏航速度的增大，由于制動盤和摩擦片接觸區(qū)域產(chǎn)生了更大的激勵，使得不斷變化的摩擦力將振動能量不斷地饋入系統(tǒng)中，在相同工況下更容易產(chǎn)生振動，導(dǎo)致制動系統(tǒng)變形增大和輻射聲壓變大，嚴(yán)重的還會導(dǎo)致制動器的內(nèi)部結(jié)構(gòu)失去原有平衡而發(fā)生劇烈振動，加劇了偏航制動器的異響和制動器各子部件之間的摩擦，降低偏航制動器的使用壽命。在實(shí)際運(yùn)行時，偏航制動速度的增加會在系統(tǒng)啟動瞬間與偏航齒輪發(fā)生激烈的齒間沖擊，造成結(jié)構(gòu)失去平衡，加劇振動的產(chǎn)生。

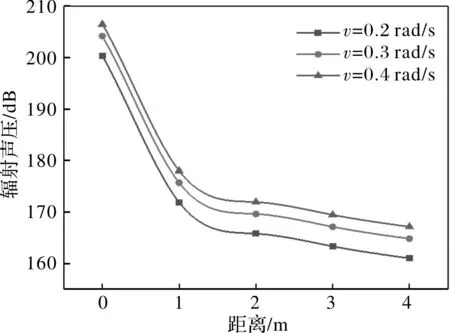
圖6 不同偏航速度下聲場變化曲線

4.3 計(jì)算數(shù)據(jù)分析

4.3.1 直觀分析

正交試驗(yàn)分析結(jié)果如表4、表5所示。對于最大輻射聲壓，極差R越大，表明該因素的水平變化對模擬結(jié)果影響越大，反之，R越小該因素影響越小。可由表5知，偏航速度對最大輻射聲壓的影響最大，偏航壓力的影響次之，摩擦系數(shù)的影響最小。設(shè)偏航速度對最大聲壓的影響系數(shù)分別為1，偏航壓力、偏航速度、摩擦系數(shù)對最大輻射聲壓的影響系數(shù)分別為0.19、1、0.03。

表4 不同工況下總聲壓的正交試驗(yàn)結(jié)果

表5 2 m輻射聲壓的極差分析

分析各工況不同水平平均值k可知，產(chǎn)生最大聲壓的偏航速度工況排序?yàn)椋?.40 rad/s>0.30 rad/s>0.20 rad/s；根據(jù)各因素水平平均值選取最優(yōu)水平組合，當(dāng)偏航壓力4 MPa、偏航速度0.2 rad/s、摩擦系數(shù)0.36，偏航制動系統(tǒng)的最高聲壓最小。

4.3.2 方差分析

正交方差分析結(jié)果，如表6所示。為了檢驗(yàn)因素顯著性，通過查詢F(n因素，n誤差)分布可知，F(xiàn)0.01(2，2)=99，F(xiàn)0.05(2，2)=19，F(xiàn)0.1(2，2)=9；將F值填入表6中，對不同工況下的聲壓進(jìn)行分析。

表6 2 m處總聲壓的正交試驗(yàn)分析結(jié)果

按照方差分析方法分析正交模擬數(shù)據(jù)，F(xiàn)值越大，該因素對模擬結(jié)果的影響越大；對表6分析可得，偏航速度對偏航摩擦的聲壓影響最大，偏航壓力的影響次之，摩擦系數(shù)的影響最小。判斷某因素對于實(shí)驗(yàn)結(jié)果是否影響顯著，通過對比F分布的臨界值，查詢F分布，即F0.01(n因素，n誤差)=F0.01(2，2)=99，若某因素F值大于F0.01(n因素，n誤差)，說明有99%的把握判斷該因素的水平對實(shí)驗(yàn)有顯著影響，反之則影響不顯著。從表6中可知，偏航速度的F值大于F0.01(2，2)，因此，方差分析結(jié)果與直觀分析結(jié)果一致，證實(shí)了試驗(yàn)數(shù)據(jù)分析的正確性。

5 結(jié)論

(1)結(jié)合偏航制動器實(shí)際尺寸、材料參數(shù)的特性，結(jié)合偏航制動器實(shí)際運(yùn)行工況，利用聲學(xué)有限元法模擬制動過程，得到了制動系統(tǒng)的聲學(xué)輻射聲壓分布云圖。

(2)偏航制動器最大聲壓為203 dB，輻射聲壓在垂直方向由制動器中心位置向四周輻射，水平方向聲壓成環(huán)狀梯度分布并逐漸減小；垂直方向聲壓衰減緩慢，故加強(qiáng)偏航制動器垂直方向的降噪。

(3)2 m處的最大聲壓在1 375 Hz處，其值為168 dB，3～5 kHz的連續(xù)噪聲與復(fù)模態(tài)結(jié)果相同；偏航制動器的噪聲屬于低頻尖叫噪聲，與偏航制動系統(tǒng)的動態(tài)失穩(wěn)有關(guān)。

(4)偏航速度對摩擦片的輻射聲壓分布的影響最大，偏航壓力的影響次之，摩擦系數(shù)的影響最小；偏航壓力、偏航速度、摩擦系數(shù)對最大輻射聲壓的影響系數(shù)分別為0.19、1、0.03。