黏土水泥漿流變本構模型及其時變特性研究

田慶浩

(1.北京中煤礦山工程有限公司,北京100013;2.礦山深井建設技術國家工程研究中心,北京100013)

注漿漿液始終是注漿技術的核心研究內容之一,隨著世界上各個國家尤其是中國地下工程建設的飛速發展,注漿法的應用變得愈加廣泛,國內外科研工作者在注漿擴散理論方面也做了不少的研究工作。早期的研究者從流體力學方面分析了單液水泥漿在裂隙中的擴散方程,隨著技術的進步,近年來有不少學者采用理論推導、數值模擬或模型試驗的方法,對注漿擴散規律進行了各種研究,對注漿理論的發展和現場起到積極的作用[1-3]。李術才等[4]研究了水泥-水玻璃漿液和改性水泥漿液2種漿液黏度的時變特性;何濤等[5]則研究了生物膠、緩凝劑等在恒定剪切速率與變化剪切速率下對漿液黏度的影響;阮文軍等[6]則通過室內試驗分析發現,不同水灰比的水泥漿液分屬3種不同流型。

針對各類黏土水泥類漿液的流變性能也有學者進行了研究,鄭晨等[7]通過室內試驗對黏土-水泥漿在不同溫度下的黏度及凝結時間的變化規律進行了研究;王星華[8-9]認為黏土-水泥漿漿液是帶屈服值的假塑性流體,本構模型符合改進的雙曲模型,但未考慮剪切速率及時間因素的影響;劉杰等[10]通過流變儀對層流狀態下不同配比的黏土水泥漿的流變參數進行了試驗研究,同樣也未考慮時間因素的影響。上述3篇文獻所研究黏土水泥漿未添加凝結劑,由黏土及水泥組成。韓春雨等[11]針對添加水泥及水玻璃的黏土水泥漿進行了本構關系試驗,認為其為賓漢流體,但對于不同配比黏土水泥漿的流型并未進行詳細的研究。

黏土水泥漿是當前注漿工程中應用最為廣泛的注漿材料之一,由黏土漿及少量水泥、水玻璃組成。該漿液具有性價比高、可注性好、耐久性及堵水效果好等優點,在井筒預注漿、地面區域治理等眾多領域得到了廣泛的應用[12-14]。注漿是一個持續的過程,漿液的本構關系及流變性則是指導研究漿液擴散規律的重要基礎條件,但針對黏土水泥漿的研究仍較少且多未考慮時間因素的影響。探究漿液的本構關系及模型參數隨時間的變化規律對于研究漿液性質以及漿液在裂隙擴散的過程具有重要意義[15-18]。

1 黏土水泥漿本構模型試驗

流變特性及流動規律的研究是漿液研究最為重要的問題之一,而本構方程的建立和流變參數的確定更是研究流體流動和流變特性的基礎。目前國內外學者提出了很多本構模型,但能夠準確描述黏土水泥漿的模型還有待研究探索,故本研究設計本構試驗探究能夠準確描述黏土水泥漿的本構模型。

1.1 試驗配比設計

首先根據現場施工經驗選取4種常用配比,如表1所示。這4種配比漿液由稀至稠分布均勻,能夠覆蓋常用配比漿液,充分體現黏土水泥漿漿液特性。

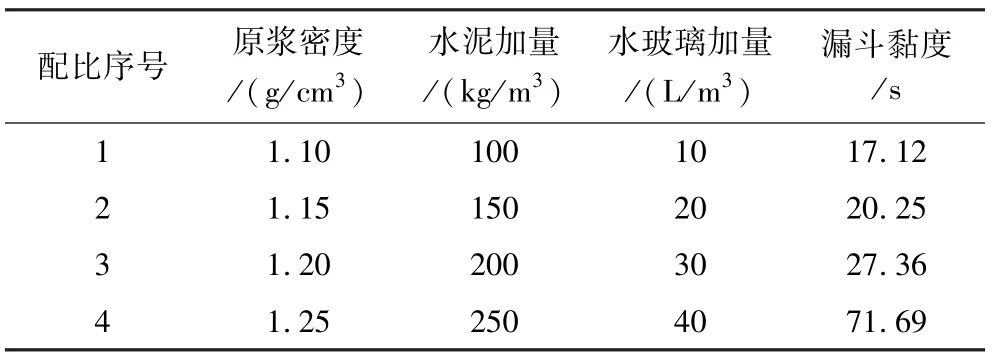
表1 本構試驗配比Table 1 Constitutive test ratio

1.2 試驗材料

1.2.1 黏 土

黏土取自施工項目現場,并經實驗室造漿除砂(含砂量小于3%)后用于室內試驗,黏土成分及性能分析結果如表2所示。

表2 試驗用黏土成分及性能分析結果Table 2 Test clay composition and performance analysis results

1.2.2 水 泥

水泥為中聯集團生產的基準水泥,水泥標準符合GB 8076-2008,產品型號為P·I 42.5硅酸鹽水泥,并做防潮保存,主要成分檢驗結果如表3所示。

表3 試驗用水泥主要成分組成Table 3 Main composition of cement for test

1.2.3 水玻璃

水玻璃為鈉質水玻璃,濃度37°Bé,密度1.338 g/cm3。

1.3 試驗步驟

按要求配置好各配比的黏土水泥漿液,通過旋轉黏度計測試每個檔位的流變數據,從讀數盤讀取對應的數據參數,經過對該參數進行計算處理,得到其對應的剪切應力;然后根據該實驗結果繪制-τ曲線,并進行擬合處理,確定各配比漿液的本構模型。

本研究將利用Origin數據分析功能中的曲線擬合功能,利用賓漢流型、冪律流型及H-B屈服假塑性流型3種非牛頓流變本構模型進行數據擬合回歸分析,對比評價不同流變本構方程擬合效果,從而確定黏土水泥漿的本構模型。其中,賓漢流體本構方程可表示為τ=τ0+;冪律流體方程表示為τ=;HB模型為τ=τ0+。各式中τ為剪切應力,τ0為屈服應力,μ為塑性黏度,K為稠度指數,為剪切速率,n為冪律指數。

擬合效果評價采用調整相關系數平方Adj.R2以及殘差平方和RSS2個參數進行分析。其中Adj.R2稱為調整相關系數平方,該參數的數值越靠近1則表示相互間的緊密程度越高;RSS稱作殘差平方和,RSS的值越小,就可以認為該組數據的相關程度越好。

1.4 本構模型試驗結果分析

分析配比1～配比4漿液擬合數據及擬合參數,如圖1、表4、圖2所示,可以發現賓漢流型及H-B屈服假塑性流體能夠準確描述黏土水泥漿的流變本構方程,冪律流體擬合效果均有所欠缺。又因為,賓漢流體的本構方程為線性方程,而H-B屈服假塑性流型的本構方程為冪指數型函數,故綜合擬合效果并從考慮簡化計算的角度,可以認為4種配比黏土水泥漿模型符合賓漢流型。

圖1 配比1～4漿液流變擬合曲線對比Fig.1 Comparison of slurry rheological fitting curves of ratio 1～4

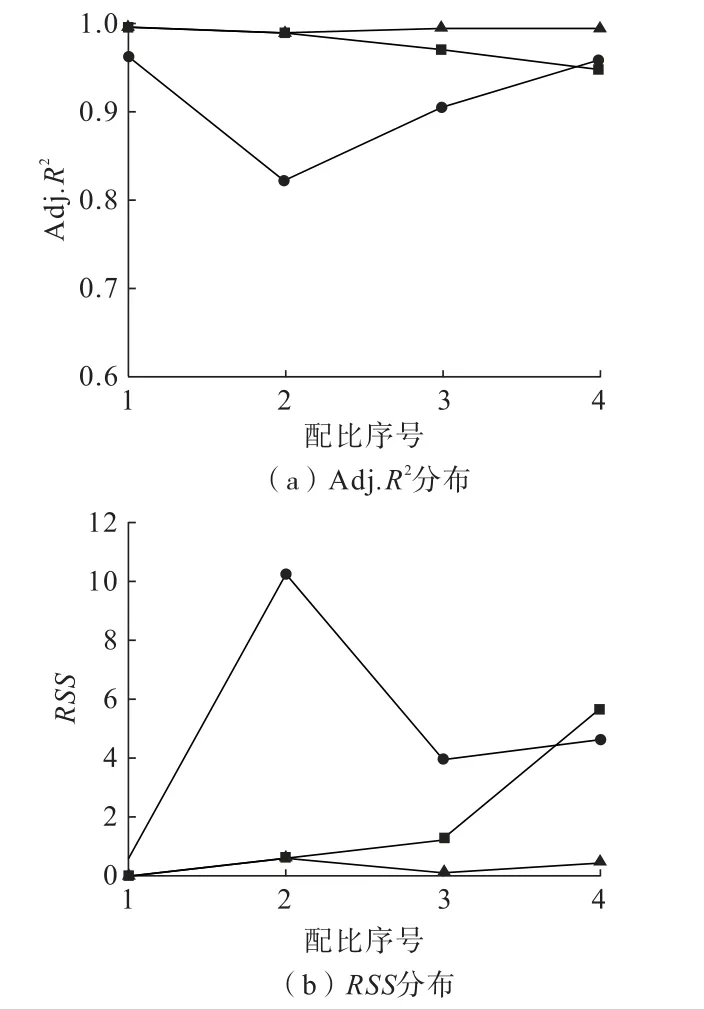
圖2 配比1～4擬合參數分布Fig.2 Ratio 1～4 fitting parameter distribution

表4 配比1～4本構模型擬合結果Table 4 Fitting results of ratio 1～4 constitutive models

2 黏土水泥漿裂隙層流擴散理論分析

前文通過試驗分析認為黏土水泥漿的本構模型符合賓漢模式,本構關系可以用方程τ=τ0+來表示。因此,本節便以賓漢流型為基礎,推導黏土水泥漿裂隙層流注漿壓力與擴散距離間函數關系。

2.1 裂隙模型

賓漢流體在裂隙層流時,假設漿液沿x軸方向流動,擴散距離用L表示,設y方向的裂隙開度為b,層流流核區高度為2y0,如圖3所示。

圖3 裂隙層流示意Fig.3 Schematic of fracture laminar flow

2.2 裂隙擴散規律理論分析

令u為流速,ρ為流體密度,τ為附加應力,P為壓強,fx為x方向的質量力。漿液在裂隙中流動的N-S運動方程:

不可壓縮流體的連續性方程:

法向應力協調方程:

對于單向單裂隙模型,因裂隙y方向寬度遠大于裂隙開度,故忽略y方向邊界對于流體運動的影響,uy=uz=0;所以:

由連續方程,并根據單向流動條件,可知:

由于定常流動條件,所以:

對于賓漢流體漿液粘度粘滯性的影響遠大于慣性的影響,假設裂隙x方向為相對地面水平方向,故忽略質量力fx影響,則fx=0。簡化得到運動方程:

積分可得:

式中,τw為側壁處的剪應力;ΔP為壓差。

在不考慮時變特性條件下,漿液的本構關系可以表示為

則

由式(5)條件,代入式(7),更換積分變量可得:

該式便為黏性流體流速分布方程。

根據式(5)知,側壁處漿液切應力最大,且當切應力τ小于屈服應力τ0區域內,漿液不流動,此時漿液流速便為0。因此,漿液產生流動的前提是τw＞τ0,即

屈服應力發生在固液兩相的相互接觸面處,故代入邊界條件y=y0時,τ=τ0。根據側壁處邊界條件,y=h,u=0,代入式(5),可得流核高度:

可見,流核區高度與漿液壓差、屈服應力及擴散距離等相關。

在漿液所承受的注漿壓力恰好達到屈服應力開始流動時,此刻壓力差表示為ΔP0,則

對比式(5)、式(9)及式(10),可以得到:

根據前文研究,黏土水泥漿符合賓漢模型,本構方程可以表示為

根據式(8)可得漿液梯速區流速:

代入式(5),整理可得:

對于流核區流速,將y=y0,代入式(13)可得:

根據對稱性原則對截面(-h,h)區域,即整個截面梯速區及流核區積分,可求得截面均速:

計算得:

簡化方程中高階項可以得到:

又針對一展度為a的矩形裂隙,在恒定注漿量q注漿過程中,漿液在裂隙則保持恒定流速。因此,可以求得截面流速:

聯立式(16)、式(17),解該聯立方程,并將式(9)代入,可以得到壓力差與擴散距離的函數關系式:

通過分析式(18),可以發現黏土水泥漿漿液擴散過程中,進出口壓力差ΔP除了受裂隙大小以及漿液擴散距離L影響外,還與屈服應力τ0及塑性粘度μ密切相關,因此有必要進一步研究2個參數對漿液本構關系及擴散規律的影響。

3 黏土水泥漿本構模型參數時變特性試驗

通過試驗及理論分析可知,黏土水泥漿的本構模型符合賓漢模式,可以用方程τ=τ0+來表示,且裂隙層流擴散注漿壓力符合式(18)的擴散規律。在實際裂隙擴散過程中注漿漿液始終處于流動狀態,單次注漿時間基本都在數小時及以上。故設計試驗探究流動狀態下黏土水泥漿本構模型參數隨時間的變化情況,以建立黏土水泥漿時變擴散方程。

3.1 試驗步驟

研究選取上文4種代表性配比黏土水泥漿,按漿液配置標準流程在實驗室配置好后,利用JJ-5型砂漿攪拌機并設置在低速模式,對漿液進行連續攪拌以模擬漿液的連續流動狀態,并每1 h從攪拌缸取樣一次利用旋轉粘度計進行流變試驗。

3.2 試驗結果分析

3.2.1 本構模型方程的時變特性

如圖4、表5所示,通過對流動狀態下黏土水泥漿的本構模型隨時間的變化情況進行試驗研究可知,不同密度、不同粘稠度的4種配比黏土水泥漿漿液的本構方程隨流動時間增加均呈現屈服應力和塑性黏度的增大的特性,且各配比漿液的流變模型均可以保持賓漢流型且不隨流動時間而改變。

圖4 配比1～4漿液不同時刻流變擬合曲線對比Fig.4 Comparison of rheological fitting curves of ratio 1～4 slurry at different times

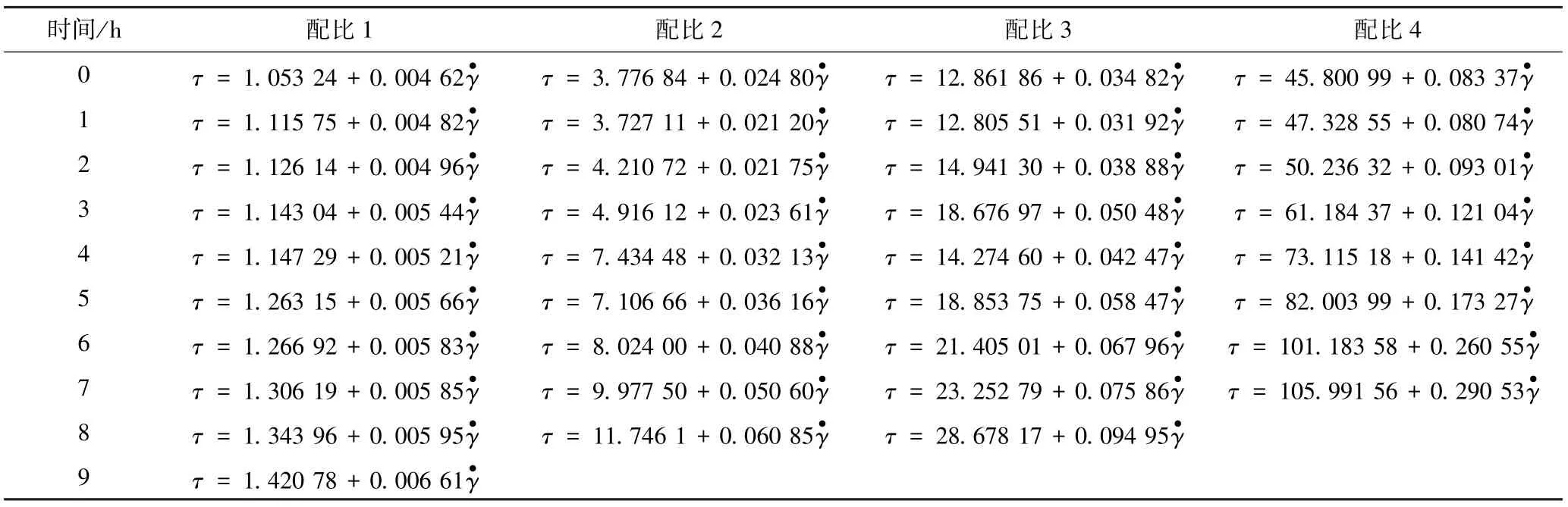
表5 配比1～4不同時刻擬合本構方程Table 5 Ratio of 1～4 different time fitting constitutive equation

3.2.2 本構模型參數的時變特性分析

3.2.2.1 屈服應力的時變特性

屈服應力τ0表示流變曲線的截距,也是漿液在流動過程中需克服的最小剪切應力,漿液剪切應力在到達該值前不會產生流動。通過前文漿液本構時變試驗的擬合結果,便可以得到在連續流動狀態下,漿液屈服應力τ0的時變數據。

通過對4種配比漿液屈服剪切應力進行時變特性分析,發現屈服應力均隨時間呈指數增長,如圖5、表6所示,且隨著漿液密度及粘稠度的增加,屈服應力逐漸增大。通過冪指數函數τ0=τ00eAt進行擬合處理,相關程度較高,各配比擬合參數Adj.R2值分別為0.956 0、0.960 8、0.870 9、0.973 6。因此,認為黏土水泥漿的漿液屈服應力符合冪指數模型,同時可以得到各配比漿液屈服應力的時變函數關系式。

圖5 配比1～4屈服應力時變方程擬合曲線Fig.5 Fitting curves of yield stress time-varying equation of ratio 1～4

表6 配比1～4屈服應力時變方程Table 6 Time-varying equation of yield stress for ratio 1～4

3.2.2.2 塑性黏度的時變特性

塑性黏度μ表示賓漢流體本構曲線的斜率,能夠反映層流時泥漿中各相(固、液、氣3相)間的內摩擦力大小情況,表征流體中的凝膠結構在受破壞后恢復保持原有狀態的能力。賓漢流體漿液在某一時刻的塑性粘度值和牛頓流體類似,只和液體本身的性質有關,不隨剪切速率的變化而變化,是表征賓漢流體流變特性的主要參數之一。

分析各配比漿液的塑性黏度隨流動時間的變化情況,可以發現其隨時間同樣呈冪指數增長規律,且隨著漿液不同配比間粘稠度的提高而增長愈加快速。利用冪函數μ=μ0eBt對塑性黏度時變規律進行擬合處理,擬合度較高,各配比擬合方程如圖6、表7所示。

圖6 配比1～4塑性黏度時變方程擬合圖線Fig.6 Fitting curves of plastic viscosity time-varying equation of ratio 1～4

表7 配比1～4塑性黏度時變方程Table 7 Time-varying equation of plastic viscosity of ratio 1～4

3.3 建立黏土水泥漿的時變本構方程

通過以上內容的分析得到了黏土水泥漿的屈服應力及塑性黏度2個參數的時變函數關系式,在此基礎上,便可以賓漢模型為基本模式建立黏土水泥漿時變本構方程。

黏土水泥漿的本構方程可以表示為τ=τ0+,又已知屈服應力隨時間變化的函數關系式可表示為τ0=τ00eAt,塑性黏度隨時間變化函數為μ=μ0eBt,式中參數A、B分別可以定義為黏土水泥漿漿液屈服應力以及塑性黏度的時變系數;τ00、μ0可以分別定義為初始屈服應力、初始塑性黏度。因此可以推導得到考慮時變因素的黏土水泥漿時變本構方程,表達式為τ=τ00eAt+μ0eBt。

根據試驗結果,可以依次可以得到各配比漿液的時變本構方程,列于表8。

表8 配比1～4時變本構方程Table 8 Ratio 1～4 time-varying constitutive equations

3.4 構建考慮本構時變特性的裂隙擴散方程

當前已知在流動過程中,黏土水泥漿屈服應力τ0及塑性粘度μ表現出時變特性,且時變規律分別符合如下模式:

于是將式(19)代入式(18),便可以得到考慮時變特性的黏土水泥漿單裂隙擴散壓力差與擴散距離間關系式:

同時,可以得到考慮漿液時變影響的注漿壓力與擴散距離間關系式:

式中,P為注漿壓力;P靜為靜水壓力;τ00為初始屈服應力;A為屈服應力時變系數;t為擴散時間;h為裂隙開度b的一半;q為注漿泵量;μ0為初始塑性粘度;B為塑性黏度時變系數;a為裂隙展度;L為擴散距離。

4 結 論

(1)根據試驗結果,黏土水泥漿的流變模型與賓漢流型及H-B屈服假塑性流型相關程度更好,冪律流型的擬合效果有所欠缺,綜合考慮擬合數據及簡化計算等因素,可以認為黏土水泥漿為賓漢流體,本構方程可以表示為τ=τ0+,這為黏土水泥漿時變規律探索及其他流變特性的研究奠定了基礎。

(2)研究發現,黏土水泥漿本構參數中的屈服應力τ0和塑性粘度μ隨流動時間的延長逐步增大,符合冪指數型的函數增長模式,可分別表示為τ0=τ00eAt、μ=μ0eBt,且流動過程中本構模型能夠保持賓漢流型而不隨時間改變。

(3)通過理論分析建立了考慮時變特性的黏土水泥漿時變賓漢本構模型τ=τ00eAt+μ0eBt,并以此推導構建了考慮黏土水泥漿時變特性的裂隙注漿擴散方程,該方程的建立可為指導黏土水泥漿或其他符合賓漢流型的漿液的裂隙注漿擴散提供參考。