基于馬爾可夫優化的高效用項集挖掘算法

鐘新成，劉昶，趙秀梅

基于馬爾可夫優化的高效用項集挖掘算法

鐘新成1，2*，劉昶2，趙秀梅1

（1.長治學院 計算機系，山西 長治 046000； 2.中國科學院 沈陽自動化研究所，沈陽 110169）（?通信作者電子郵箱cy12016596@czc.edu.cn）

基于樹型和鏈表結構的高效用項集挖掘（HUIM）算法通常需要指數量級的搜索空間，而基于進化類型的挖掘算法未能充分考慮變量間的相互作用，因此提出一種基于馬爾可夫優化的HUIM算法（HUIM-MOA）。首先，采用位圖矩陣表示數據庫和使用期望向量編碼，以實現對數據庫的快速掃描和效用值的高效計算；其次，通過計算優勢個體間的互信息估計馬爾可夫網絡（MN）結構，并根據它們的局部特性使用吉布斯采樣以產生新的種群；最后，為防止算法過快陷入局部最優和減少高效用項集的缺失，分別采用種群多樣性保持策略和精英策略。在真實數據集上的實驗結果表明，相較于次優的基于粒子群優化（PSO）的生物啟發式HUI框架（Bio-HUIF-PSO）算法，在給定較大最小閾值的情況下，HUIM-MOA可以找到全部的高效用項集（HUI），收斂速度平均提升12.5%，挖掘HUI數平均提高2.85個百分點，運行時間平均減少14.6%。HUIM-MOA較進化型HUIM算法有更強的搜索性能，能有效減少搜索時間和提高搜索質量。

高效用項集挖掘；馬爾可夫網絡；位圖矩陣；吉布斯采樣；精英策略

0 引言

數據挖掘旨在從數據庫提取有用的模式或訓練模型，以理解過去或預測未來。頻繁項集挖掘（Frequent Itemset Mining， FIM）是一項被研究廣泛的數據挖掘任務，且應用于許多領域。它可以被視為分析數據庫的一般任務，以查找一組事務數據庫中同時出現的項［1］。盡管頻繁模式挖掘有用，但假設它依賴頻繁模式雖有趣卻并不適用于許多應用程序。比如，在事務數據庫中，模式｛牛奶，面包｝可能是頻繁的，但該模式是無趣的，因為該模式在日常生活中常見且不會帶來太多的利潤。另一方面，模式｛茅臺，魚子醬｝可能是非頻繁的，但它有著豐厚的利潤。因此，為了在數據庫中找到更多有趣的模式，可以考慮其他方面的因素，如利潤或效用。若項集在數據庫中的效用不小于用戶指定的最小效用閾值，則稱該項集為高效用項集（High Utility Itemset， HUI）。高效用項集挖掘（High Utility Itemset Mining， HUIM）在現實生活中應用廣泛，如在購物超市中挖掘高利潤商品組合模式、在電商平臺產生的數據流中挖掘購物者的高消費模式和在移動通信數據中挖掘高消費客戶群體的消費規律等。

HUIM算法大致可分為精確算法和進化算法（Evolutionary Algorithm， EA）兩種類型［2］。前者致力于找到所有的HUI，但同時承受指數量級的搜索空間，隨著問題規模增大，此類算法的運行時間變得不可接受；后者致力于快速找到大部分的HUI，但不能保證找到所有的HUI。日常生活中，找到所有HUI并非必要，若能在較短的時間內找到大部分HUI，對指導商家作出決策也非常有意義。

已有學者提出了幾種EA實現HUIM。Kannimuthu等［3］等提出一種基于遺傳算法（Genetic Algorithm，GA）的HUIM算法，首次使用EA研究HUIM；但是它沒有考慮HUI是挖掘更多滿足最小效用閾值的項集而非簡單地尋找最優的HUI，所以在一些數據集上的挖掘效果不理想。Zhang等［4］改進了基于GA的高效用算法，提出了基于個體改善、鄰域探索和種群多樣性保持等策略的挖掘算法，實驗結果表明在這些策略的綜合作用下，在不同數據集上的各項指標都有較大改善。Lin等［5-6］提出一種基于粒子群優化（Particle Swarm Optimization， PSO）的HUIM算法，該算法提出粒子編碼長度由高事務加權效用1項集決定，在此種編碼下能有效地縮小搜索空間并提高搜索效率。Song等［7-8］和Wu等［9］提出基于人工魚群［7］、人工蜂群［8］和蟻群［9］的HUIM算法，這些算法都模擬群體智能以進化種群，挖掘質量各有所長。Pazhaniraja等［10］提出一種基于布爾代數的灰狼算法挖掘HUI，在運行時間、收斂速度和挖掘數量上都有較好表現。Song等［11］提出了基于生物進化啟發的HUIM框架，包含GA、PSO算法和蝙蝠算法，這些算法采用通用框架，只在具體編碼和操作上略有差異，其中位圖表示、位圖操作和非期望向量剪枝策略都提高了遍歷解空間的速度，并且在各數據集上都有良好的表現，基于該框架的算法大幅提高了挖掘效率。然而，基于EA的HUIM算法挖掘所有滿足最小效用閾值的HUI仍然耗時較長：一方面EA通常沿著上一代最優值的方向搜索，這可能使某些HUI在迭代過程中被遺漏；另一方面，基于EA的HUIM算法相較于搜索新的HUI通常效率較低。

馬爾可夫優化算法（Markovian Optimization Algorithm，MOA）［12］是分布估計算法（Estimation of Distribution Algorithm， EDA）［13］的一個分支。該類算法是一種基于概率論的優化算法，主要思想是分析優勢群體的分布模型，并用它影響新一代群體的分布，可以更有效地處理非線性、高維復雜問題［14］。此外，EDA還有其他EA不具備的優勢，如自適應算子、問題結構和先驗知識的利用等［15］。

目前，較少有學者將MOA應用于HUI的相關挖掘工作。為提高挖掘效率，本文提出一種基于馬爾可夫優化的HUIM算法（HUIM Algorithm based on Markovian Optimization， HUIM-MOA），主要特點有：1）使用位圖表示、位圖操作和非期望編碼檢驗策略加速HUI的挖掘；2）通過計算變量間的互信息估計馬爾可夫網絡（Markov Network， MN）結構并構建各變量的條件概率模型［16-17］；3）通過吉布斯采樣法產生新的個體；4）通過種群多樣性保持策略防止算法陷入局部最優，采用精英策略減少HUI的缺失。

1 相關工作

1.1　HUIM

表1事務信息

Tab.1　Transaction information

表2外部效用

Tab.2　External utility

其中：（）表示內部效用，（）表示外部效用。

例如：（｛，｝，10）=（，10）×（）+（，10）×（）=2×6+4×1=16。

定義2 項集在數據庫中的效用記為（），如式（3）所示，式（3）也作為HUIM的目標函數：

例如：（｛，，｝）=（｛，，｝，1）+（｛，，｝，3）=（，1）+（，1）+（，1）+（，3）+（，3）+（，3）=3+18+6+6+1+6=40。

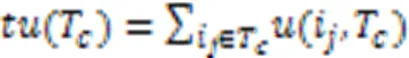
定義4 事務數據庫中項集經常出現在多個事務中，將各事務效用進行累加得到的效用稱為事務加權效用，記做（），如式（5）所示：

例如：（｛，｝）=（1）+（3）+（5）+（8）+（10）=27+13+16+55+72=183。

定義5 根據用戶偏好，將最小效用閾值系數設為，如果項集的效用值不小于最小效用值，記為，則稱項集是HUI。定義如式（6）所示：

例如：假設=25%，則=（27+66+13+11+16+10+101+55+15+72）×25%=386×25%=96.5。由于（｛，｝）=183>96.5，所以｛，｝是HUI；由于（｛，，｝）=60<96.5，所以｛，，｝不是HUI。

定義6 如果項集滿足（）>，則稱為高事務加權效用項集，記為HTWUI。包含個項目的HTWUI記為-HTWUI。例如：假設=115，則高事務加權效用1項集（1-HTWUI）的挖掘結果如表3所示。

表3高事務加權效用1項集的挖掘結果

Tab.3　Mining results for 1-HTWUI

注：NO（）表示非高事務加權效用1項集，YES（）表示是高事務加權效用1項集，（）里面的數字是事務加權效用值。

事務加權效用具有3個重要性質，尤其當某1項集為低事務加權效用項集時，可以對搜索空間進行大范圍剪枝，從而縮小搜索空間，這也是基于EA的HUIM算法經常采用的一個初始挖掘手段。

性質1 對于某項集總有（）>（），表明項集的事務加權效用是對本身效用值的向上估計。

性質3 若（）<，則項集和它的超集都是低效用項集。

1.2　MOA

MOA是EDA的一個分支。有別于EA利用群體智能引導種群進化，EDA通過捕捉變量間的相互依賴關系構建概率模型，從而獲得先驗概率以引導種群進化。局部馬爾可夫特性強調了由MN結構編碼的條件概率可以直接用于采樣，而不需要建立復雜的聯合概率分布模型。此外，MOA采用吉布斯抽樣法進行采樣并包含了溫度參數，該參數可以平衡對搜索空間的探索和利用，并允許算法處理由循環表示的相互作用。局部馬爾可夫特性被定義為變量之間的鄰域關系，如式（7）所示：

其中N是節點x的相鄰節點集。式（7）表明節點x的條件概率可以由它的鄰域節點集N定義，N有時也被稱為馬爾可夫毯。基于馬爾可夫特性的EDA工作流程如下所示：

步驟1 隨機生成含個解的總體。

步驟3 用中數據估計MN結構。

步驟5 用新的種群替代舊種群，然后返回步驟2，直到滿足終止條件。

從上述流程可以看出，MOA的關鍵步驟為確定MN結構和根據局部馬爾可夫條件概率進行采樣。通常可用不同方法確定一個無向圖結構，MOA采樣一種基于熵的互信息方法確定MN結構，即估計解中每對變量的互信息以創建一個互信息矩陣。若每對變量間的互信息高于某一設定的閾值，則它們可成為相鄰節點；另外，為了防止網絡結構過于復雜，任一節點的相鄰節點數應設置一個上限。兩個變量和之間的互信息由式（8）給出：

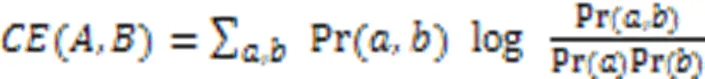
估計網絡結構后，再估計每一節點的條件概率，最后根據條件概率采樣新的種群。吉布斯抽樣法是MOA中的一類蒙特卡洛采樣方法，它始于一個隨機解和一個固定的迭代次數，然后隨機選擇解中的某一變量并計算它在MN結構下的條件概率以得到該變量的某一新的取值，接著用輪盤賭的方法采樣其他變量的新值，當達到迭代次數時，輸出新解。在吉布斯抽樣法中，條件概率一般估計為：

假設變量是二值變量，一般只需計算變量取值為1的概率，因為取0的概率可以根據互斥性給出，式（9）可寫為：

為了實現MOA中基于溫度的吉布斯抽樣法，式（9）的條件概率可估計為：

對于二值變量，則x取1的條件概率可由它的相鄰節點估計為：

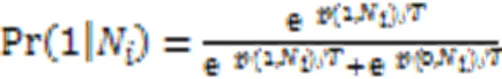
2 本文算法

本文提出的HUIM-MOA依賴于位圖數據庫表達并涉及以下幾個主要步驟：種群初始化、選擇優勢個體、構建概率模型、吉布斯采樣、種群多樣性保持策略和精英策略。本章首先介紹兩個重要的準備工作：位圖表示和期望向量編碼。

2.1　位圖表示和期望向量編碼

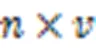
表4展示了表1對應數據庫的位圖表示。

表4對應事務信息的位圖表示

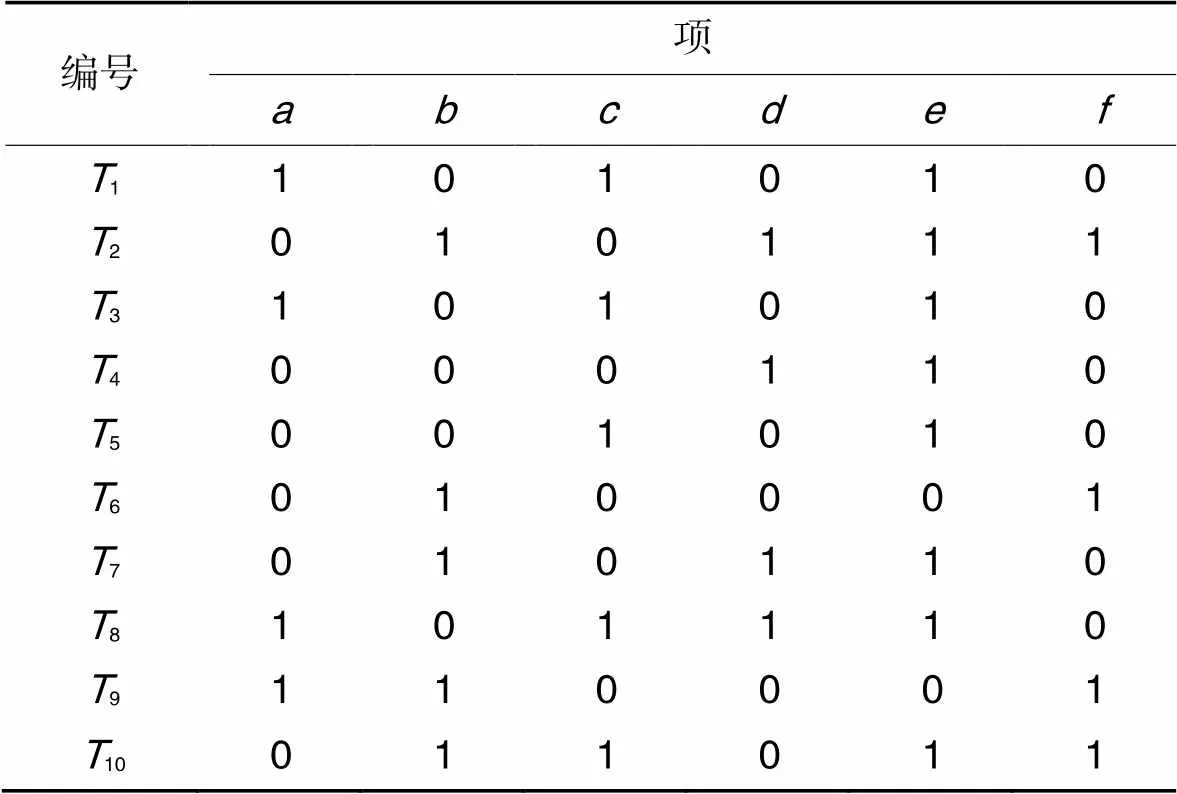
Tab.4　Bitmap representation of corresponding transaction information

定義7 若項集編碼向量的位圖覆蓋全為0，則稱該向量為非期望編碼向量（UnPromising Encoding Vector， UPEV），反之則稱為期望編碼向量（Promising Encoding Vector， PEV）。UPEV表示該編碼向量對應的項集在數據庫中不存在，不可能成為HUI，刪除UPEV的過程稱為非期望編碼向量修剪策略（UPEV Cut strategy， UPEVC）。UPEVC的偽代碼如算法1所示。

算法1 PEV_Check（）。

輸入 編碼向量；

輸出 期望編碼向量。

1）計算中1的位數

3）=（1）

4） for=2 todo

8） 改變中的一位i狀態

9） end if

11） end for

12） return

HUIM-MOA中使用了兩種策略修剪搜索空間：其一是使用事務加權向下閉包屬性刪除低效用項集以有效減小搜索空間和提高計算速度［11］；其二是使用UPEV修剪事務數據庫中不存在的項集。在上述兩種策略下，MOA編碼的長度完全由1-HTWUI決定。例如，假設=115，則1-HTWUI有｛，，，，｝，相應編碼長度為5。每個編碼位置對應一個項，編碼為1表示該項出現在該位置；編碼為0則表示不出現。圖1表示項集｛，｝是一個潛在的解。

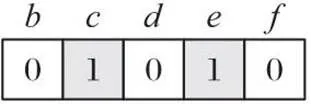
圖1　編碼示例

在種群初始化階段，每個個體根據1-HTWUI的TWU初始化，若某1-HTWUI的TWU較高，則它被選中的概率相應也更高。算法2展示了這個初始化過程。在算法2中，每個個體各編碼位置初始被指派為0，接著根據每個1-HTWUI的TWU的大小采用輪盤賭的形式確定該位置1出現的概率。每個位置取1的概率由式（14）決定：

若一個個體生成完畢，則加入種群，如此反復，最后返回初始種群。

算法2 Pop_Init（）。

輸入 數據集，種群規模；

輸出 第一代種群。

1）遍歷數據集，并刪除1?LTWUI

2）將數據集表示為bitmap

3） for=1 todo

4） 產生隨機數num

5） 運用輪盤賭方式產生一個位向量

6） ifnum>1 then

7）=PEV_Check（）

8） 改變中的一位i狀態

9） end if

10） end for

2.2　構建概率模型

種群初始化后計算相應項集的效用值，若高于設定閾值，則加入HUI，并對該種群按照效用值從高到低進行排序，按設定比例截取前面的優良個體組成新的數據集。接著使用數據集估計MN結構。構建概率模型的偽代碼如算法3所示。

算法3 Pro_Model（）。

輸入 優勢個體組成的種群，重要系數，最大相鄰節點數；

輸出 MN結構。

1）=len（［0］）

2）0

3） for=1 to，=+1 todo

4） 用式（8）估計變量x和x的互信息m

5） end for

6）計算平均互信息

7） for=1 to，=+1 todo

8） ifm>then

9） 在變量x和x間創建一條邊

10） end if

11） end for

12） for=1 todo

13） if NB>then

14） 保留x的互信息排名前個相鄰節點

15） end if

16） end for

2.3　吉布斯采樣

算法4 Gibbs_sample（）。

輸入 MN結構，種群規模，冷卻系數，迭代系數；

輸出 新一代種群。

2）=1

4） 隨機產生一個解=（1，2，…，x）

6） 從中隨機選擇一個x

7） 以概率P（1|NB）置x為1；←用式（12）

8） end for

9）=PEV_Check（）

11） end while

12） return

2.4　精英策略和種群多樣性保持策略

2.5　HUIM-MOA算法總體設計及實例演示

HUIM-MOA的偽代碼如算法5所示。步驟1）～4）是算法的初始化，5）～21）是整個算法的迭代過程，其中6）～12）是篩選HUI的過程，13）是按效用值由高到低進行排序，14）是按設定比例選擇優勢個體，15）是構建概率模型，16）是執行吉布斯采樣，17）～18）是執行精英策略和種群多樣性保持策略。

算法5 HUIM-MOA。

輸入 事務數據集，最小效用閾值；

輸出 所有的高效用項集。

1） Pop_Init（）

2）=1

5） while≤_do

6） for each individualdo

7） 確定與位圖向量對應的項集

11） end if

12） end for

13）按的第一元素進行排序

14）按比例截取的第二元素組成新種群

15） Pro_Model（）

16） Gibbs_Sample（）

17）執行精英策略

18）執行多樣性保持策略

19）++

20） end while

21） return

根據前述數據庫、效用表和位圖舉例。假設=115，被挖掘的1-HTWUI如表3所示，則個體編碼長度為5，表5展示了種群初始化所得的10個個體，經過HUI篩選后，將項集：166，：216，：131分別加入高效用項集。接著按效用值排序并按1∶2選取優勢個體，得到新的位圖如表6所示。

表5初始種群

Tab.5　Initial population

表6截斷后優勢個體組成的種群

Tab.6　Population composed of dominant individuals after truncation

首先，計算各變量兩兩間的互信息。設定=1.2，經計算平均互信息為0.117 8，其中有、、、、間互信息大于平均互信息，分別為0.5、0.118 5、0.118 5、0.118 5、0.118 5，故這些變量之間可以分別連一邊，于是可以估計MN結構如圖2所示。

圖2　MN結構

其次進行吉布斯采樣。該采樣從一個隨機解=（1，0，1，0，1）開始，隨機選定一維變量4==0；接著用變量的條件概率采樣新的，此時的鄰邊集為｛｝，且此時=1。設定=4，于是在=1的情況下取1的概率計算為：

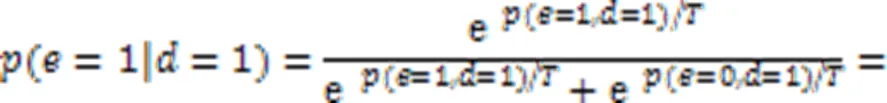
由式（15）計算結果可知，此時以0.524 8的概率取1。令的新值為1，新的個體變為=（1，0，1，1，1），再隨機取一維變量2==0，的鄰邊集為｛，｝，且此時=1，=1。于是在此情況下取1的概率可計算為：

令的新值取0，新的個體變量為=（1，0，1，1，1），依此繼續采樣，直到迭代完畢獲得一個新個體。假設最終新個體是=（1，0，1，1，1），經PEVC檢測后存在，則不用修改；若不存在，則作相應修改。如此下去，便得到了新的種群。

最后，執行精英策略和種群多樣性保持策略，這里不再贅述。

3 實驗與結果分析

將HUIM-MOA和目前最先進的基于EA的HUIM算法進行實驗對比以綜合評估算法性能。這些算法包括基于PSO的生物啟發式HUI框架（Bio-inspired HUI Framework based on PSO，Bio-HUIF-PSO）、基于GA的生物啟發式HUI框架（Bio-inspired HUI Framework based on GA，Bio-HUIF-GA）、基于或/非樹結構PSO的HUIM算法（HUIM algorithm based on PSO with a OR/NOR tree structure，HUIM-PSO_tree）、基于人工魚群的HUIM算法（HUIM algorithm based on Artificial Fish swarm， HUIM-AF）。性能指標包括收斂速度、挖掘的HUI數、挖掘全部或不同比例HUI所需要的運行時間。

3.1　實驗環境和數據集

實驗所用電腦配置如下：Intel Core i5-6402P CPU 2.8 GHz，16 GB內存，64位Windows 7操作系統，編程語言為Java。用Mushroom、Connect、Foodmart和Chainstore這4個數據集進行實驗對比，4個數據集均來自開源社區SPMF［18］。Foodmart數據集包含了消費者在商店的購物記錄；Connect數據集記錄了游戲步數；Chainstore數據集記錄了美國加州一家大型連鎖雜貨店的客戶交易數據；Mushroom數據集包含了各類蘑菇及其相應特征，如氣味、形狀等。各數據集詳情如表7所示。

表7數據集詳情

Tab.7　Details of datasets

對于Chainstore數據集上的對比實驗，最大迭代次數設置為2 000；其他數據集上的對比實驗，最大迭代次數設置為1 200，種群規模統一設置為40。Chainstore數據集上的迭代次數設置更大的原因是它為大型稀松數據集，在給定最小閾值下找到全部或絕大多數HUI需要更多的迭代次數。HUIM-MOA的相關參數設置如下：平均互信息重要系數設為1.5，溫度冷卻速率系數設為4，種群截斷比例設置為1∶2。

3.2　收斂性對比

用每個算法在10次獨立運行后獲得的平均結果比較收斂性能。5個算法在各數據集相應閾值上的收斂效果如圖3所示。從圖3可見，HUIM-MOA在各數據集上都達到最高的收斂速度，Bio-HUIF-PSO次之。HUIM-MOA的收斂速度較Bio-HUIF-PSO平均提升了12.5%，主要原因是采用的種群多樣性保持策略能有效防止算法陷入局部最優；此外，吉布斯采樣溫度系數的合理設置也能讓算法在探索和開發中取得平衡，因此，HUIM-MOA算法始終保持探索新的HUI的能力。由于HUIM-PSO_tree、HUIM-AF在數據集Chainstore上的運行時間超過3 h，對比它們的收斂性已無意義，故圖3（d）中沒有它們的收斂曲線。

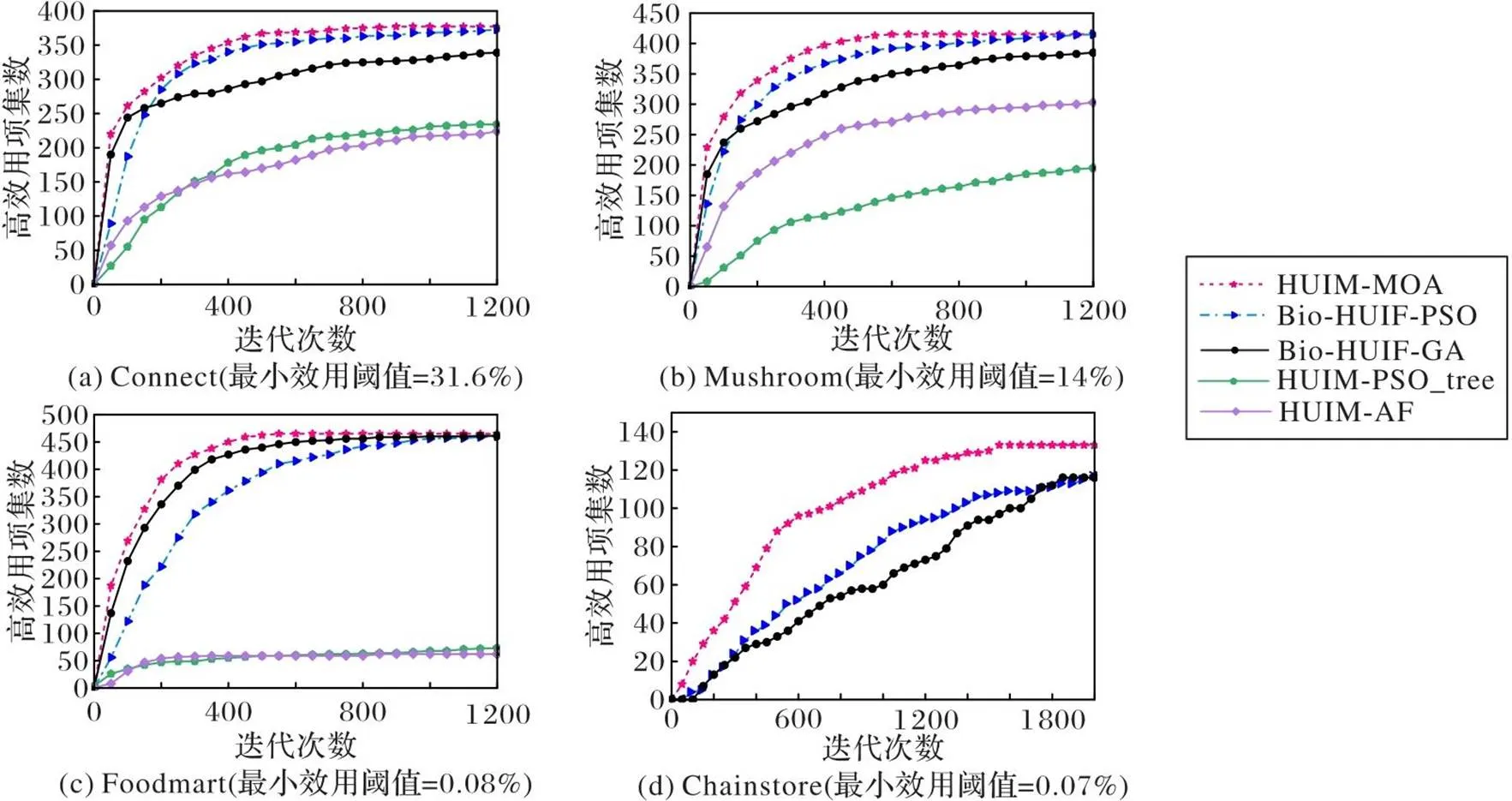
圖3　各算法在給定閾值下的收斂情況

3.3　運行時間

圖4展示了5個算法在各數據集不同閾值下的運行時間。可以看出，HUIM-MOA在4個數據集上的運行時間都是最少的，Bio-HUIF-PSO的運行時間次之。HUIM-MOA在各數據集上的運行時間較Bio-HUIF-PSO平均減少了14.6%。HUIM-PSO_tree、HUIM-AF整體運行時間都較長，在Chainstore這樣的大型稀松數據集上運行時間超過3 h；HUIM-PSO_tree雖然采用OR/NOR tree的結構避免了不必要項集的產生，但相較于位圖表示和期望向量編碼依然更費時。

3.4　挖掘到的HUI數

在稠密數據集上閾值一般設置得較高，而在稀松數據集上閾值一般設置得較低，這是由于在稠密數據集上若設置較低閾值，則滿足要求的HUI會大幅增加，在設定的迭代過程中難以找到絕大多數的HUI；若在稀松數據集上設置較高閾值，則可能導致沒有滿足要求的HUI，如在稀松數據集Foodmart上，當閾值設定為0.22%時，則沒有滿足要求的HUI。表8展示了5個算法在各數據集不同閾值下挖掘的HUI數的百分比。

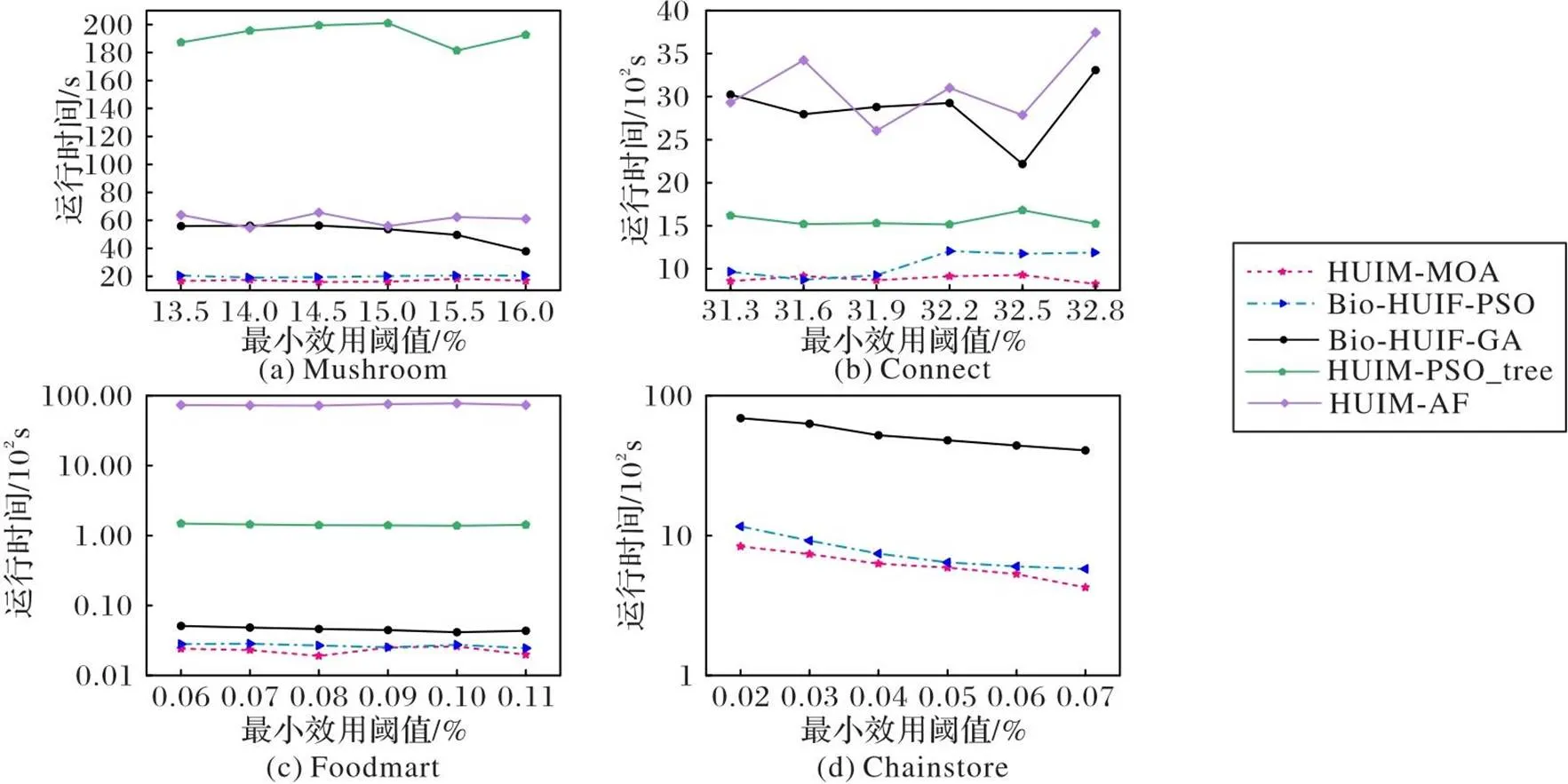
圖4　各算法在給定閾值下的運行時間

表8對比算法在各數據集不同閾值下挖掘的HUIs的百分比 單位：%

Tab.8　Percentage of HUIs mined by comparative algorithms with different thresholds for each dataset unit：%

可以看出，當給定閾值較大時，HUIM-MOA可以挖掘所有的HUI，相較于次優的Bio-HUIF-PSO，它挖掘的HUI平均數的百分比在4個數據集上提高了2.85個百分點。這是由于HUIM-MOA采樣了MN結構的局部特性，它充分利用變量間的依賴關系，從而能找到更多的HUI；此外，種群多樣性保持策略和精英策略也能在一定程度上防止算法陷入局部最優，實現更廣泛的搜索，使得算法在后期也能持續搜索新的HUI。值得注意地，在稀松數據集Foodmart上，當閾值設定為0.06%時，兩個基于BIO-HUIF框架的算法都只能找到近一半的HUI，HUIM-PSO_tree、HUIM-AF表現則更差，而HUIM-MOA能找到93.84%的HUI，這也充分體現了HUIM-MOA處理高維稀松數據集的優越性。在大型稀松數據集Chainstore上，各算法能找到的HUI的比例都大幅降低，這表明進化型算法處理大型稀松數據集存在一定的劣勢。由于HUIM-PSO_tree、HUIM-AF的運行時間超過3 h，對比它們的挖掘數已無意義，故表8中未顯示它們的挖掘百分比。

4 結語

本文算法（HUIM-MOA）通過分析優勢個體間的互信息估計MN結構，并用MN的局部特性估計每個變量的條件概率，使得MOA相較于基于全局特性的算法更易實現；接著使用帶溫度下降的吉布斯采樣法生成新的種群；為提高算法的運行效率，采用了位圖表示法和期望向量編碼；為使種群不過快陷入局部最優和減少HUI的缺失，分別采用了種群多樣性保持策略和精英策略，加強HUIM-MOA的搜索能力；同時，互信息重要系數和溫度冷卻系數的恰當設定也使算法在開發和探索上達到一個平衡。從4個真實數據集上的實驗結果可以看出，無論是在稠密集還是稀松集上，HUIM-MOA在收斂速度上比其他4個算法更高、運行時間更少，挖掘HUI數也最多。

未來將進一步優化基于MN的概率建模和采樣過程，使算法的運行時間更少，同時還將嘗試用其他類型的EDA與EA進行結合的方法挖掘HUI。當然，其他更合理更有效的剪枝策略、搜索策略也是下一步要重點研究的問題。

[1] CHEE C-H， JAAFAR J， AZIZ I A， et al. Algorithms for frequent itemset mining： a literature review［J］. Artificial Intelligence Review， 2019， 52： 2603-2621.

[2] FOURNIER-VIGER P， LIN J C-W， TRUONG-CHI T， et al. A survey of high utility itemset mining［M］// High Utility Pattern Mining. Cham： Springer， 2019： 1-45.

[3] KANNIMUTHU S， PREMALATHA K. Discovery of high utility itemsets using genetic algorithm with ranked mutation ［J］. Applied Artificial Intelligence， 2014， 28（4）： 337-359.

[4] ZHANG Q， FANG W， SUN J， et al. Improved genetic algorithm for high-utility itemset mining ［J］. IEEE Access， 2019， 7： 176799-176813.

[5] LIN J C-W， YANG L， FOURNIER-VIGER P， et al. Mining high-utility itemsets based on particle swarm optimization［J］. Engineering Applications of Artificial Intelligence， 2016， 55： 320-330.

[6] LIN J C-W， YANG L， FOURNIER-VIGER P， et al. A binary PSO approach to mine high-utility itemsets ［J］. Soft Computing， 2017， 21： 5103-5121.

[7] SONG W， LI J， HUANG C. Artificial fish swarm algorithm for mining high utility itemsets ［C］// Proceedings of the 12th International Conference on Swarm Intelligence. Cham： Springer， 2021： 407-419.

[8] SONG W， HUANG C. Discovering high utility itemsets based on the artificial bee colony algorithm ［C］// Proceedings of the 2018 Pacific-Asia Conference on Knowledge Discovery and Data Mining. Cham： Springer， 2018： 3-14.

[9] WU J M-T， ZHAN J， LIN J-W. Mining of high-utility itemsets by ACO algorithm ［C］// Proceedings of the 3rd Multidisciplinary International Social Networks Conference on SocialInformatics 2016， Data Science 2016. Cham： Springer， 2016： Article No. 44.

[10] PAZHANIRAJA N， SOUNTHARRAJAN S， KUMAR B S. High utility itemset mining： a Boolean operators-based modified grey wolf optimization algorithm ［J］. Soft Computing， 2020， 24（21）： 16691-16704.

[11] SONG W， HUANG C. Mining high utility itemsets using bio-inspired algorithms： a diverse optimal value framework［J］. IEEE Access， 2018， 6： 19568-19582.

[12] SHAKYA S， SANTANA R. MOA-Markovian optimisation algorithm［M］// Markov Networks in Evolutionary Computation. Berlin： Springer， 2012： 39-53.

[13] 王圣堯，王凌，方晨，等. 分布估計算法研究進展［J］. 控制與決策， 2012， 27（7）： 961-966，974.（WANG S Y， WANG L， FANG C， et al. Advances in estimation of distribution algorithms ［J］. Control and Decision， 2012， 27（7）： 961-966，974.）

[14] SEBAG M， DUCOULOMBIER A. Extending population-based incremental learning to continuous search spaces ［C］// Proceedings of the 1998 International Conference on Parallel Problem Solving from Nature. Cham： Springer， 1998： 418-427.

[15] LARRA?AGA P， ETXEBERRIA R， LOZANO J A， et al. Optimization in continuous domains by learning and simulation of Gaussian networks ［C］// Proceedings of the 2th Genetic and Evolutionary Computation Conference. San Mateo：Morgan Kaufmann， 2000：201-204.

[16] SANTANA R. A Markov network based factorized distribution algorithm for optimization ［C］// Proceedings of the 2003 European Conference on Machine Learning. Cham： Springer， 2003： 337-348.

[17] SHAKYA S， McCALL J. Optimization by estimation of distribution with DEUM framework based on Markov random fields［J］. International Journal of Automation and Computing， 2007， 4： 262-272.

[18] FOURNIER-VIGER P， LIN J C-W， GOMARIZ A， et al. The SPMF open-source data mining library version 2 ［C］// Proceedings of the 2016 Joint European Conference on Machine Learning and Knowledge Discovery in Databases. Cham： Springer， 2016：36-40.

High utility itemset mining algorithm based on Markov optimization

ZHONG Xincheng1，2*， LIU Chang2， ZHAO Xiumei1

（1，，046000，；2，，110169，）

To address the problems that the High Utility Itemset Mining （HUIM） algorithms based on tree and link table structures often consume search spaces of orders of magnitude， and the evolutionary type-based mining algorithms fail to fully consider the interactions between variables， an HUIM algorithm based on Markov Optimization （HUIM-MOA） was proposed. Firstly， a bitmap matrix for expressing database and expectation vector encoding were used to achieve fast scanning of the database and efficient computation of utility values， respectively. Then， the Markov Network （MN） structure was estimated by computing the mutual information among dominant individuals and new populations were generated by using Gibbs sampling according to their local characteristics. Finally， population diversity preservation strategy and elite strategy were used to prevent the algorithm from falling into local optimum too quickly and to reduce the missing of high utility itemsets， respectively. Experimental results on real datasets show that compared with Bio-inspired High Utility Itemset Framework based on Particle Swarm Optimization （Bio-HUIF-PSO）algorithm， HUIM-MOA can find all the High Utility Itemsets （HUIs） when given a larger minimum threshold， with on average 12.5% improvement in convergence speed， 2.85 percentage point improvement in mined HUI number， and 14.6% reduction in running time. It can be seen that HUIM-MOA has stronger search performance than the evolutionary HUIM algorithm， which can effectively reduce the search time and improve the search quality.

High Utility Itemset Mining (HUIM); Markov network; bitmap matrix; Gibbs sampling; elite strategy

This work is partially supported by Science and Technology Innovation Project of Colleges and Universities in Shanxi Province in 2022 （2022L517）.

ZHONG Xincheng， born in 1987， M. S.， lecturer. His research interests include data mining， reinforcement learning.

LIU Chang， born in 1973， Ph. D.， associate research fellow. Her research interests include data mining， schedule optimization.

ZHAO Xiumei， born in 1970， M. S.， lecturer. Her research interests include software testing.

TP301.6

A

1001-9081（2023）12-3764-08

10.11772/j.issn.1001-9081.2022121844

2022?12?09；

2023?02?28；

2023?03?03。

2022年度山西省高等學校科技創新項目（2022L517）。

鐘新成（1987—），男，湖南長沙人，講師，碩士，主要研究方向：數據挖掘、強化學習；劉昶（1973—），女，遼寧沈陽人，副研究員，博士，主要研究方向：數據挖掘、調度優化；趙秀梅（1970—），女，山西高平人，講師，碩士，主要研究方向：軟件測試。