微元法在高中物理教學中的應用探討

梁曉芳

(安徽省太和一中,安徽 阜陽 236600)

高中物理教學中,微元法也就是分割累積法,屬于微積分思想的具體體現.將其應用到物理教學的各個環節,能夠幫助學生形成良好的思維邏輯,降低學生物理知識學習以及物理解題的難度[1].教師要在微元法的具體應用上加大研究,為提升物理教學實效提供保障.

1 微元法的概述

微元法屬于一種科學的思維方法,與微積分相類似.微元法主要就是將研究對象分割成若干個微小的單元,確保每個微小的單元都能夠滿足同一物理規律,通過分割單元的方式,讓變量逐漸趨向于常量,進而將不容易確定的變量轉變為比較明確的常量,降低問題分析的難度.微元法在高中物理教學中的應用時,主要包括構建微元對象以及從微元推廣至整體這兩個部分,學生在學習物理知識以及解物理題的過程中,通過對多個微小單元的物理量進行深入分析,并構建相應的物理模型,進而實現對知識的理解與對物理題的解答[2].

2 微元法在高中物理教學中應用的價值

微元法在高中物理教學中的應用,是創新物理教學思想的關鍵舉措,教師應深入了解微元法的內涵,了解微元法在教學中應用的具體方法,同時能夠掌握微元法的具體應用價值,從而在教學中加大對微元法應用策略的研究,發揮微元法的應用價值全面提升物理教學的實效.具體來看,高中物理教學中應用微元法的價值主要體現在以下幾方面:(1)突出了學生學習的主體地位.傳統的高中物理教學中,將微元法應用到物理教學中,教師的教學形式發生改變,從以往的直接灌輸轉變為引導學生運用微元法進行自主探究和學習,激發了學生學習的主觀能動性,強化了學生在學習上的主體地位.(2)有利于提升課堂教學實效.微元法的應用對提升教學的實效有重要的幫助,一方面,利用微元法能夠激發學生自主學習的積極性,使學生能夠積極配合教師布置的學習任務,提高課堂互動的有效性;另一方面,通過運用微元法能夠讓學生從具象思維逐漸向抽象思維過度,使學生形成良好的思維品質,對物理知識的內涵能夠進行深入分析和研究,提升物理知識的理解與掌握程度.此外,還能夠降低學生物理解題的難度,提升解題的準確率.由此可見,微元法在高中物理教學中的有效運用對提升課堂教學的實效有重要幫助.(3)有利于促進學生綜合發展.在高中物理教學中培養學生全面發展是教學的核心目標,微元法的應用不僅可以提升課堂教學的質量,讓學生對物理知識有深度的理解和掌握,提高學生解題的準確率,與此同時,通過微元法的應用能夠使學生掌握科學的學習方法,提高其自主學習能力、邏輯思維能力等,為學生課后的自主學習與終身發展提供了保障[3].

3 微元法在高中物理教學中具體的應用策略

3.1 在公式推導中運用微元法

物理教師可以應用微元法組織學生進行物理公式的推導,讓學生深入了解物理公式的形成過程,實現學生對物理公式的理解性記憶.

3.1.1應用微元法推導勻變速直線運動的位移公式

在勻變速直線運動中速度是持續累加的,位移與速度和時間有關,運用微元法進行位移公式的推導,如果將初始的速度作為該段位移的平均速度,將其與時間相乘后得到的位移是圖1中的甲,可見其與實際的位移存在較大的差距.如果將該段位移所使用的時間分成5等分,將每段時間的初始速度作為該段時間的平均速度,并與各段時間相乘后累加,得出的位移是圖1中的乙,可以發現雖然與實際位移也存在一定的差距,但是相對于甲而言差距要減少很多.如果將該段位移所使用的時間分成15等分,同樣將各段時間的初始速度作為平均速度,與時間相乘后累加,得出的位移是圖1中的丙,相對于乙圖中的位移而言要更接近實際位移.按照這種分割方式,將該段位移中所使用的時間分成無數等分,并將各段位移進行累加,得出的位移是圖1中的丁,會無限接近于實際位移.從圖中可以看到,每個圖中各時間段位移與實際位移相差的是梯形與矩形之間相差的三角形部分,如果分割的分數越多,這一差值就會越小,當分割無數分時,這一差值就可以忽略不計,由此可以得出公式:

(2)vt=v0+at.

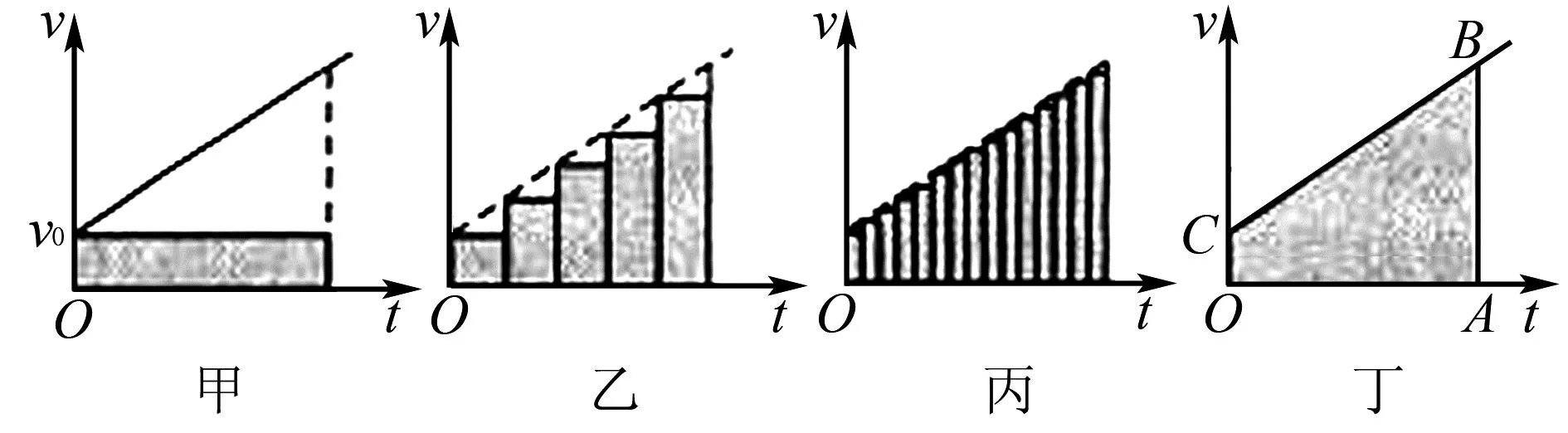
圖1 位移與速度和時間關系圖

3.1.2應用微元法推導彈性勢能公式

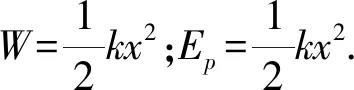
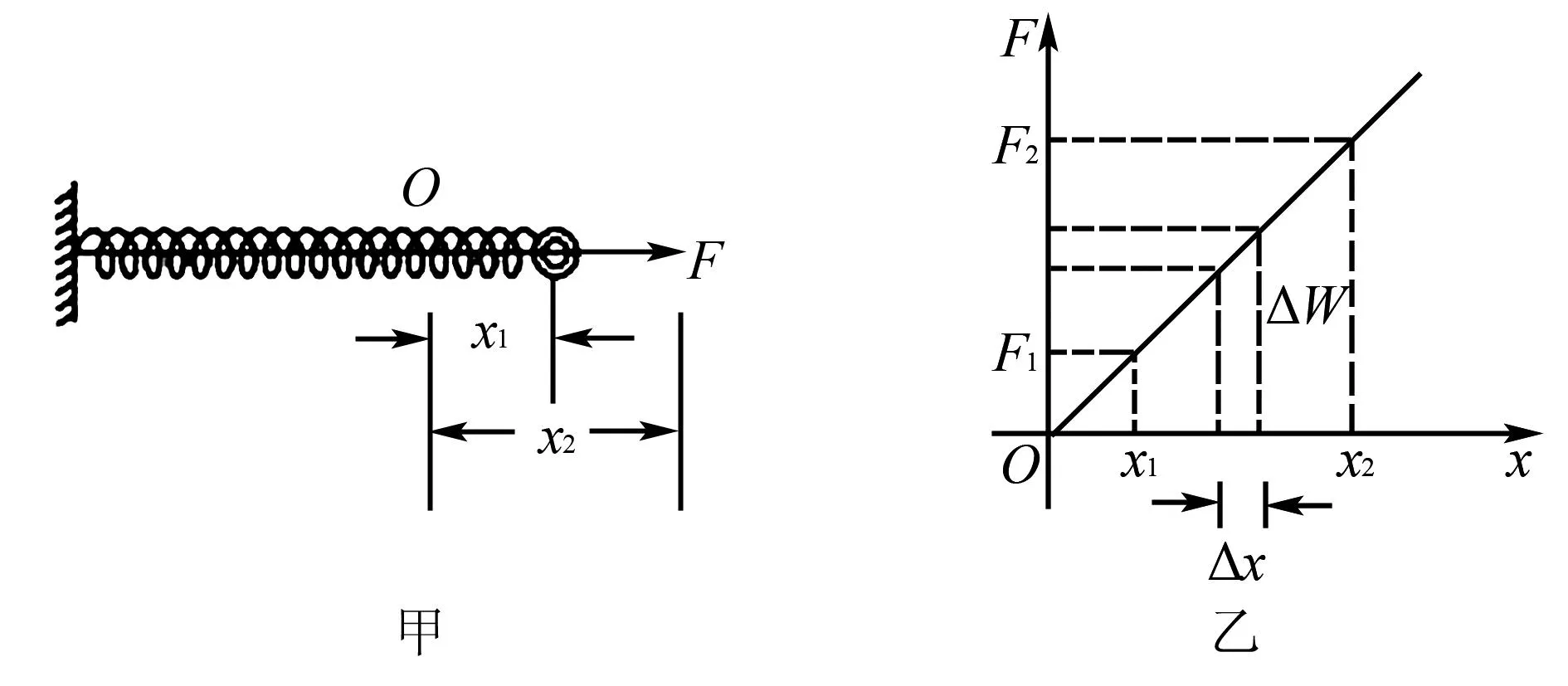
圖2 彈力與伸長量關系圖

3.2 在物理解題中運用微元法

高中物理解題中應用微元法,能夠有效降低學生的解題難度,特別是題目中涉及一些不均勻變化的物理量時,往往不能直接用已有的物理規律來解決.這時,就可以應用微元法進行分析,物理教師要指導學生學會運用微元法進行物理解題,提升學生物理解題的準確度.

3.2.1連續體問題中的質量微元

在物理解題中,如果研究的對象不能用典型的物理模型來分析,就需要教師引導學生應用微元法,從研究對象中提取微元,并對其受力情況進行深入分析,從而將其轉化為常規的物理模型運用相應的物理規律進行處理[4].

例1運動員在進行水上運動表演的過程中,穿戴的噴射式懸浮飛行器將水袋中的水豎直向下噴出,能夠讓運動員處于懸停的狀態(如圖3).運動員和裝備加在一起的質量M為100 kg,下噴水的噴嘴單個面積S為0.008 m2.假設重力加速度g=10 m/s2,水的密度ρ=1× 103kg/m2,求噴水速度v的大小.

圖3 噴射式懸浮飛行器懸停狀態圖

圖4 Δt時間內所噴出的水量圖

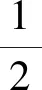
在運用微元法分析該題的過程中,構建的是流體類的“柱體”模型,教師要引導學生對該解題步驟進行分析,幫助其掌握具體的微元法解題的流程.

3.2.2均勻分布的帶電體中的電荷量微元

在高中物理教學中,解有關電場方面的題目時,如果靜電場中帶電體無法被看成是點電荷,這時需要用到微元法對帶電體進行分解,提取電荷量微元,將其作為題目研究的對象,從而降低解題的難度.運用微元法解帶電體相關物理題,主要是處理對稱性帶電體所產生的電場強度以及電勢等問題.

例2如圖5,有一根均勻的絕緣帶電棒,總長度是L,其所帶電的總量為+Q.在該帶電棒的中垂線以及延長線上有兩點M、N,距離中垂線與帶電棒相交點O的距離相等,都為a,求出M、N兩點的電場強度.

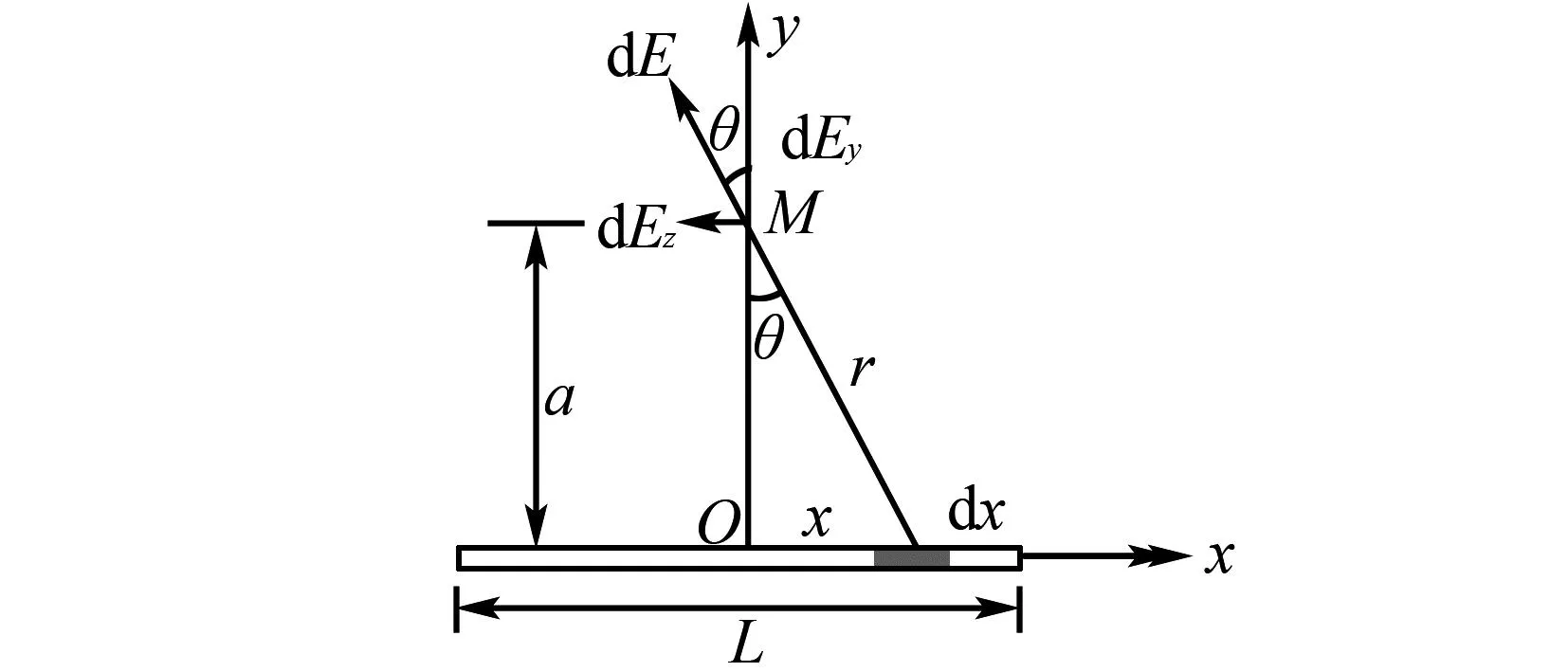
圖5 絕緣帶電棒長度與電場強度圖

高中物理解題中微元法的應用比較廣泛,通過微元法的具體應用情況可以看到,該方法實際上就是分割累積法,屬于微積分思想的具體體現.

綜上所述,高中物理教學中,有效應用微元法能夠幫助學生逐漸形成良好的抽象思維,促進學生的深度學習,同時對提升課堂互動有效性、提高課堂教學質量也有重要的幫助.