再談抽象函數對稱問題的求解與拓展

侯有岐

(陜西省漢中市四○五學校,陜西 漢中 723312)

抽象函數是指沒有給出具體的函數解析式或圖象,只給出一些函數符號及其滿足條件的函數,如函數的定義域、解析遞推式、特定點的函數值、特定的運算性質等.它是高中函數部分的難點,也是大學高等數學函數部分的一個銜接點.

下面筆者以2022年高考數學全國卷中的三道抽象函數為例,先探究試題背景,然后對相關試題進行對比研究,整理出抽象函數對稱性、奇偶性、周期性問題的一般化性質,以期拋磚引玉.

1 試題呈現

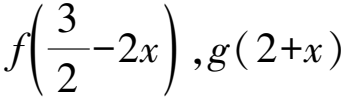
C.f(-1)=f(4) D.g(-1)=g(2)

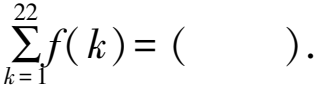
A. -21 B. -22 C. -23 D.-24

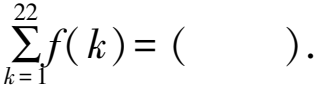
A. -3 B. -2 C. 0 D.1

這三道試題都是涉及抽象函數及其導函數之間的對稱性(軸對稱、中心對稱)和周期性的綜合題.這類問題主要考查學生數學語言的轉化能力、推理運算能力以及抽象思維能力.解決這類問題的關鍵就是要把隱蔽在抽象函數中的對稱性和周期性挖掘出來并應用于解題過程中[1].

下面我們先來研究有關抽象函數的一般性質,為解決相關問題探尋更有效的策略.

2 性質探究

2.1 抽象函數對稱性的幾個重要結論

事實上,根據函數圖象的概念及對稱圖形的定義,不難證明以下結論.

推論1 若函數y=f(x)定義域為R,且滿足條件:f(a+x)=f(a-x),則函數y=f(x)的圖象關于直線x=a對稱.

推論2 若函數y=f(x)定義域為R,且滿足條件:f(x)=f(2a-x)),則函數y=f(x)的圖象關于直線x=a對稱.

可以看出,函數f(x)滿足的條件中x的系數一個為1,另一個為-1,相應解析式的自變量相加除以2,可得y=f(x)圖象的對稱軸方程.

推論3 若函數y=f(x)定義域為R,且滿足條件:f(a+x)=f(a-x), 又若方程f(x)=0有n個根,則此n個根的和為na.

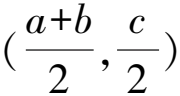
推論2若函數y=f(x)定義域為R,且滿足條件:f(a+x)+f(a-x)=0(a為常數),則函數y=f(x)的圖象關于點(a,0)對稱.

可以看出,上面的f(x)滿足的條件中x的系數一個為1,另一個為-1時,函數f(x)圖象存在對稱中心.

推論1 函數y=f(x-a)與函數y=f(a-x)的圖象關于直線x=a對稱.

推論2 函數y=f(a+x)與函數y=f(a-x)的圖象關于直線x=0對稱.

上述常用結論中四個性質的本質完全不同.性質1是探討一個函數的圖象本身關于某條直線的對稱問題,即自身軸對稱問題;性質2是探討一個函數的圖象本身關于某點的對稱問題,即自身中心對稱問題;性質3是探討兩個函數的圖象關于某條直線的對稱問題,即相互軸對稱問題;性質4是探討兩個函數的圖象關于某點的對稱問題,即相互中心對稱問題.解題時要注意它們的區別.

進一步拓展問題,不難證明上述四個性質的更一般形式:

2.2 抽象函數周期性的幾個重要結論

在以下各式中,x取其定義域內的任意值,且a,b,T為非零常數,a≠b,則不難證明如下結論:

性質9若f(x±T)=f(x),則y=f(x)的周期為T,kT(k∈Z,k≠0)也是函數的周期.

性質10若f(x+a)=f(x+b),則y=f(x)的周期為|b-a|.

性質11若f(x+a)=-f(x),則y=f(x)的周期為2|a|.

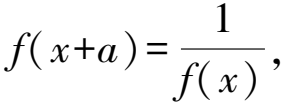
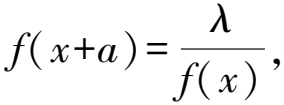
推論4若f(x+a)+f(x)=c,則y=f(x)的周期為2|a|.

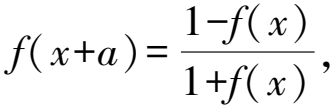
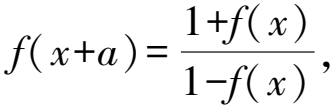
性質15若f(x+2a)=f(x+a)-f(x),則y=f(x)的周期為6|a|.

2.3 抽象函數的周期性與雙對稱性間的關系

類比正弦函數y=sinx和余弦函數y=cosx的圖象及周期,可以猜想并證明如下結論:

性質16 (兩線對稱型)設f(x)是定義在R上的函數,其圖象關于直線x=a和x=b(b>a)對稱,則函數y=f(x)的周期為2(b-a).

性質17 (兩點對稱型)設f(x)是定義在R上的函數,其圖象關于點(a,0)和點(b,0)(b>a)對稱,則函數y=f(x)的周期為2(b-a).

性質18(一線一點對稱型)設f(x)是定義在R上的函數,其圖象關于直線x=a和點(b,0)(b>a)對稱,則函數y=f(x)的周期為4(b-a).

2.4 抽象函數與導函數之間的對稱性和周期性

性質19已知函數f(x)及其導函數f′(x)的定義域為R.

(1)若f(x)關于直線x=a對稱,則f′(x)關于點(a,0)對稱.

(2)若f(x)關于點(a,t)對稱,則f′(x)關于直線x=a對稱．

證明(1)若f(x)關于直線x=a對稱,則f(a+x)=f(a-x).求導得f′(a+x)=-f′(a-x).

所以f′(x)關于點(a,0)對稱．

(2)若f(x)關于點(a,t)對稱,則f(a+x)+f(a-x)=2t.求導得f′(a+x)=f′(a-x).

即f′(x)關于直線x=a對稱.

在性質1中,當a=0,t=0時,有如下結論:

推論已知函數f(x)及其導函數f′(x)的定義域為R．

(1)若f(x)關于直線x=0即y軸對稱,則導函數f′(x)關于原點(0,0)對稱.

也就是:若f(x)是偶函數,則其導函數f′(x)是奇函數.

(2)若f(x)關于原點(0,0)對稱,則導函數f′(x)關于直線x=0即y軸對稱.

也就是:若f(x)是奇函數,則其導函數f′(x)是偶函數.

性質20已知函數f(x)及其導函數f′(x)的定義域為R.若導函數f′(x)關于直線x=a對稱,則函數f(x)關于點(a,t)對稱.

證明若f′(x)關于直線x=a對稱,則f′(a+x)=f′(a-x).有f(a+x)+f(a-x)=2t.

即函數f(x)關于點(a,t)對稱.

注意若f′(x)關于點(a,t)對稱,則f(a+x)+f(a-x)=2t,得f(a+x)-f(a-x)=2m,并非f(a+x)=f(a-x),即函數f(x)不一定關于直線x=a對稱.

性質21已知函數f(x)及其導函數f′(x)的定義域為R.若函數f(x)是周期為T的函數,則其導函數f′(x)也是周期為T的函數.

證明若函數f(x)是周期為T的函數,則f(x+T)=f(x),求導得f′(x+T)=f′(x).即導函數f′(x)也是周期為T的函數.

注意若導函數f′(x)是周期為T的函數,則f′(x+T)=f′(x),得f(x+T)=f(x)+m.故函數f(x)不一定是周期為T的函數.

例如,函數f(x)=sinx+x,f′(x)=cosx+1,導函數f′(x)是周期函數,但f(x)不是周期函數.

2.5 復合函數的奇偶性

定義1若對于定義域內的任一變量x,均有f[g(-x)]=f[g(x)],則復數函數y=f[g(x)]為偶函數.

定義2若對于定義域內的任一變量x,均有f[g(-x)]=-f[g(x)],則復合函數y=f[g(x)]為奇函數.

說明(1)復合函數y=f[g(x)]為偶函數,則f[g(-x)]=f[g(x)],而不是f[-g(x)]=f[g(x)];復合函數y=f[g(x)]為奇函數,則f[g(-x)]=-f[g(x)],而不是f[-g(x)]=-f[g(x)].

(2)兩個特例:若y=f(x+a)為偶函數,則f(x+a)=f(-x+a);若y=f(x+a)為奇函數,則f(-x+a)=-f(x+a).

(3)y=f(x+a)為偶(或奇)函數,等價于單層的函數y=f(x)的圖象關于直線x=a軸對稱(或關于點(a,0)中心對稱).

3 試題解答

根據上述結論,不難得到上述三道試題的具體解答過程如下:

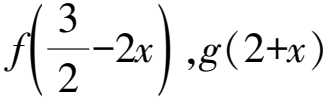
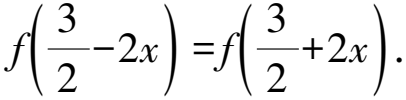
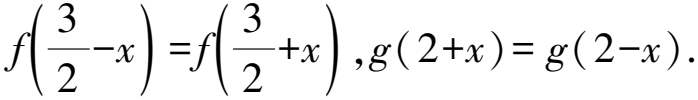
所以f(3-x)=f(x),g(4-x)=g(x).

則f(-1)=f(4),故C正確.

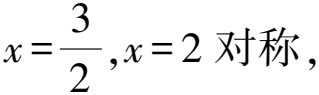
所以g(4-x)=g(x)=-g(3-x).

所以g(x+2)=-g(x+1)=g(x).

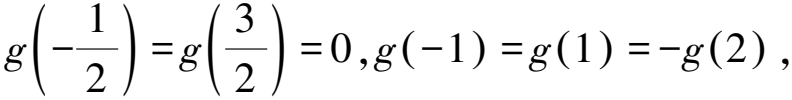
若函數f(x)滿足題設條件,則函數f(x)+C(C為常數)也滿足題設條件,所以無法確定f(x)的函數值,故A錯誤.故選BC.

點評解決本題的關鍵是轉化題干條件為抽象函數的性質,準確把握原函數與導函數圖象間的關系,準確把握函數的性質(必要時結合圖象)即可得解.

題2解析因為y=g(x)的圖象關于直線x=2對稱,所以g(2-x)=g(x+2).

因為g(x)-f(x-4)=7,

所以g(x+2)-f(x-2)=7.

即g(x+2)=7+f(x-2).

因為f(x)+g(2-x)=5,所以f(x)+g(x+2)=5.

代入得f(x)+[7+f(x-2)]=5.

即f(x)+f(x-2)=-2.

所以f(3)+f(5)+…+f(21)=(-2)×5=-10,

f(4)+f(6)+…+f(22)=(-2)×5=-10.

因為f(x)+g(2-x)=5,所以f(0)+g(2)=5,即f(0)=1,所以f(2)=-2-f(0)=-3.

因為g(x)-f(x-4)=7,所以g(x+4)-f(x)=7.

又因為f(x)+g(2-x)=5,聯立,得

g(2-x)+g(x+4)=12.

所以y=g(x)的圖象關于點(3,6)中心對稱.因為函數g(x)的定義域為R,所以g(3)=6,因為f(x)+g(x+2)=5,所以f(1)=5-g(3)=-1.

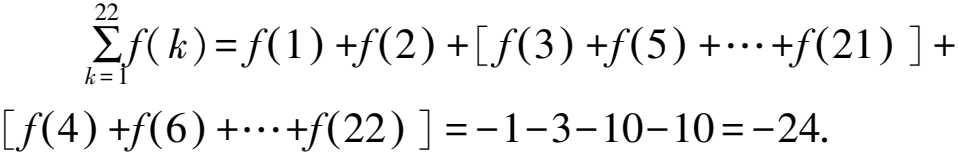
點評含有對稱軸或對稱中心的問題往往條件比較隱蔽,考生需要根據已知條件進行恰當轉化,然后得到所需的一些數值或關系式從而解題.

題3解析因為f(x+y)+f(x-y)=f(x)f(y),令x=1,y=0可得,2f(1)=f(1)f(0),所以f(0)=2.

令x=0可得,f(y)+f(-y)=2f(y).

即f(y)=f(-y).

所以函數f(x)為偶函數.

令y=1,得f(x+1)+f(x-1)=f(x)f(1)=f(x).

即有f(x+2)+f(x)=f(x+1).

從而可知f(x+2)=-f(x-1),

f(x-1)=-f(x-4).

故f(x+2)=f(x-4).

即f(x)=f(x+6).

所以函數f(x)的一個周期為6．

因為f(2)=f(1)-f(0)=1-2=-1,f(3)=f(2)-f(1)=-1-1=-2,f(4)=f(-2)=f(2)=-1,f(5)=f(-1)=f(1)=1,f(6)=f(0)=2,所以一個周期內的f(1)+f(2)+…+f(6)=0．

點評首先對題目給出的抽象函數的性質進行理解,然后通過變量賦值,把抽象函數問題轉化為具體的數學問題,從而問題得解,這是解決抽象函數問題常用的方法之一.

高考試題對高考復習教學具有很強的導向作用.本文通過對2022年高考數學全國卷中三道抽象函數問題的研究,對抽象函數的一般性質作了系統的歸納整理,從而使學生對本部分知識有了進一步的理解.只有研究高考試題的不同解法及其相關性質,并從中挖掘高考試題的導向功能,才能更好地把握復習備考的方向,提高復習斜率.