樁承臺橋墩基礎局部沖刷數值模擬研究

閆杰超，徐 華

（1.中電建江蘇勘測設計研究院有限公司，江蘇南京 211100；2.南京水利科學研究院，江蘇南京 210029）

引言

群樁結構作為海工結構（海上平臺、碼頭等）和海底結構等支撐基礎已得到廣泛應用，其下部通常由一系列單樁按一定規律排列而成，具有一定透水及減小阻水能力，相比于單墩基礎，這使得群樁基礎周圍的局部沖刷及發展過程更為特殊而復雜[1]。相對于單樁沖刷情況，群樁局部沖刷主要存在以下四種機制，即上游樁的遮蔽效應、樁間的沖刷強化效應、壓縮馬蹄渦的效應及尾渦脫落效應[2]。劉詩航等[1]從群樁基礎孔隙率角度將群樁基礎水流尾跡分為單個尾跡模式、穩定尾跡模式以及實體尾跡模式三種模式。目前，對于群樁基礎沖刷特性研究多關注下部樁基不同排列形式引起的沖刷規律或特性，而通常忽略群樁基礎墩身及承臺部分也對沖刷產生一定影響，尤其承臺高程變化將對群樁基礎局部沖刷產生舉足輕重的作用。梁森棟與張永良[3]研究復合群樁基礎沖刷特性發現，承臺吃水深度越大，總沖刷深度也越大。但隨著相對吃水深度進一步增加，局部沖刷深度增加將趨于不敏感。盧中一與高正榮[4]依托蘇通長江大橋工程，用物理水槽對群樁承臺不同入水深度引起的局部沖刷進行研究，得到了導致底部床面發生最大及最小沖深時承臺入水位置。Yifan Yang 等[5]通過物理模型試驗對群樁承臺不同入水深度引起的局部沖刷進行研究，得出不同承臺高程對局部沖刷深度影響呈先增大后減小的趨勢，并得到承臺頂高程位于泥面附近時局部沖刷深度最大的情況。眾所周知，樁承臺橋墩基礎承臺結構尺寸往往較大，且在其正常服役期間將受到不同水文情況影響，對承臺吃水深度及高程位置均帶來不利變化，這不僅使得其局部沖刷深度預測困難，也給其相關沖刷防護設計帶來難以預料的困難。承臺形狀也將影響樁承臺基礎附近水流結構，進而影響其局部深度[6]。P Gautam 等[7]研究一種橢圓形承臺基礎在不同高程條件下局部沖刷深度。Ramtin S 與Alireza M[8]通過數值模擬研究四種承臺形狀樁承臺基礎局部沖刷深度特性，得出機翼型樁承臺橋墩沖刷深度減小最大的結論，尖鼻型等具有較好氣動外形的樁承臺是控制馬蹄渦的較好選擇，可以減小橋墩基礎周圍的沖刷深度。

目前，面對樁承臺橋墩基礎正常服役期間承臺吃水深度及高程位置帶來的不利影響難題，關于其局部沖刷深度計算相關研究較少，而分析其承臺形狀對局部沖刷深度影響也不多。因此，本文基于目前樁承臺橋梁基礎存在的問題，通過建立三維水沙動力模型與理論分析計算，以研究不同承臺形狀橋墩在不同承臺高程條件下的局部沖刷特性。

1 模型建立

1.1 模型概化

本文以文獻[5]中樁承臺橋梁基礎為研究對象，其橋墩基礎由墩身、承臺及樁基復合組成。其中，墩身為矩形結構，墩寬bcol為30 mm，墩長Lcol為310 mm；承臺為矩形結構，承臺寬bpc為120 mm，承臺長Lpc為362 mm，承臺厚T為60 mm，Hc為承臺頂距離初始泥面距離（mm）；樁基基礎由排與列2×4 共8 根圓柱組成，圓柱直徑bp為25 mm，列距Sn為70 mm，排距Sn為70 mm。該研究物理模型試驗中樁承臺橋梁基礎順直布置于長25 m，寬2.4 m 及深0.6 m 模型水槽中，模型來流水深y0為0.1 m，來流流速V為0.311 m/s。模型試驗采用泥沙為均質天然石英砂，平均粒徑d50=0.84 mm，泥沙幾何標準分差gσ=1.3，樁徑?=25 mm。具體橋墩結構形式示意如圖1 所示。

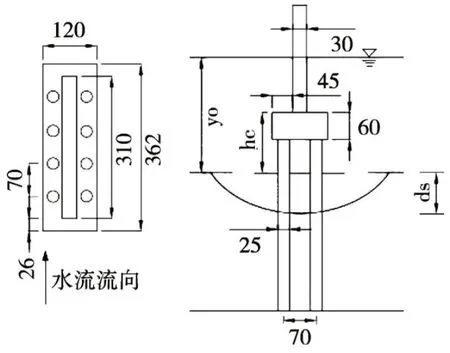
圖1 橋墩及樁基布置（單位：mm）

本文通過流體計算軟件CFD 建立的三維水沙數值模型對不同承臺高程樁承臺橋梁基礎沖刷特性（承臺頂高程ch分別為0.09 m 與0.06 m）與在相應承臺迎水面上設置梯形結構（該梯形結構其高P與承臺厚T相同，其寬W與承臺寬bpc相同，其長度即伸向迎流水流方向長度L與其高P相同，本文將此類承臺概化為梯形承臺）的局部沖刷特性展開探討研究。

其中，水槽總長4.0 m，墩前長1.65 m，墩后長0.65 m；水槽寬1.21 m，高0.5 m。模型計算水動力條件為y0=0.1 m，V=0.311 m/s。泥沙條件為中值粒徑d50=0.84 mm，密度ρ=2 650 kg/m3及休止角θ=32°，具體模擬工況及條件如表1 所示。

1.2 控制方程

1）水動力控制方程

其中，VF為流體體積分數；ρ為液體密度；(u,v,w) 為笛卡爾坐標系下(x,y,z) 的速度分量；RSOR為源匯項；(Ax,Ay,Az)、(Gx,G y,Gz)與(f x,f y,fz)分別為(x,y,z) 方向的流體面積分數、重力及單位質量的體積力；A為平均流體面積；U為(x,y,z) 方向的平均流速；F為水流體積函數，當液體充滿單位網格時，F值等于1，當單位網格為空時F值等于0。

2）泥沙運動控制方程

本文建立的數學模型中泥沙運動控制方程包括河床變形方程、推移質與懸移質方程，且該泥沙運動模型可以模擬推移質與懸移質之間的交換運動。而對于推移質方程，本文結合文獻[9]研究成果選擇Nielsen 方程，具體關于泥沙運動控制方程中參數選取可參考文獻[10]。

河床變形方程：

其中，z為床面高程；bq為泥沙單寬推移質輸移率；?為最大填空率；D為向下泥沙沉降通量；E為向上泥沙吸卷通量。

推移質運動方程：

其中：φi為無量綱泥沙推移質輸移率；β Nie為Nielsen 經驗系數，等于12.0；θ為泥沙shields 數；crθ為泥沙臨界shields 數；bc為泥沙體積分數。

懸移質運動方程：

其中：C為懸移質泥沙濃度；us為泥沙沉降流速；ε為泥沙擴散系數。

1.3 模型驗證

數值模型的驗證首先依據文獻中對單個圓墩的沖刷試驗成果，采用該文獻[11]進行數值模型驗證有兩個原因，其一是單個圓墩相對本文研究的群樁基礎沖刷較為簡單，群樁的沖刷涉及到樁群之間的干擾及遮擋作用，達到平衡需要較長的時間，將增加模型驗證的難度，為方便研究，首先可以采用單墩沖刷案例對數值模型中重要參數進行率定；其二是該文獻中水流條件及泥沙條件與與本文研究的樁承臺橋墩基礎中水流條件及泥沙條件基本相似。因此，其驗證可以說明本文采用的研究方法是科學正確的，且后續對于更復雜的樁承臺橋墩基礎沖刷模擬中不僅結合該驗證成果中參數選擇，還將采用物理試驗測量數據進行驗證。下面將對文獻[11]中試驗條件進行簡述。該物理模型水槽長為10 m，寬為1.21 m 及高0.45 m。直徑為0.1651 m 的圓墩垂直插于水槽床面，且床面鋪設0.2 m 厚均勻泥沙，泥沙中值粒徑d50為0.85 mm，密度ρ為2 650 kg/m3。同時，其相應的水動力條件水深為0.186 m，流速為0.25 m/s。數值模擬根據物理模型實際情況與上述網格、模型參數設置一致，模擬時間為4 000 s。具體驗證結果如圖2～ 3 所示。

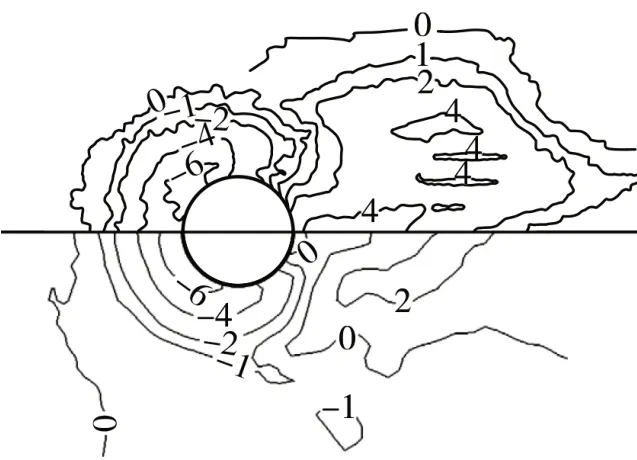
圖2 圓形橋墩平面局部沖淤變化實測結果（下）與數值模擬（上）對比

如圖2 所示可知，圓形橋墩平面局部沖刷深度與淤積深度分別為0.085 m 與0.056 m，而物理試驗實測局部沖刷深度與淤積深度分別為0.075 m 與0.041 m。從墩前沖刷范圍等深線來看，數值模擬結果與物理試驗結果基本一致，沖刷主要出現在墩前0 °至墩側80 °之間。但墩后淤積區域存在一定差異，數值模擬結果的淤積范圍及淤積高度偏大，這種差異通常與采用的RNGk-ε湍流模型密切相關，其往往不能很好的對墩后馬蹄渦系進行細致的刻畫及模擬，以致引起墩后模擬結果與實際存在一定差異。同時，從圖3 圓形橋墩局部沖淤深度變化實測結果與數值模擬對比可知，數值模型能夠相對較好的對沖刷時間演變過程進行模擬，其之間沖刷深度誤差約為11.8 %，其誤差在可接受范圍，驗證整體良好，說明建立的三維水沙數學模型中重要參數選擇較為合理，其后續樁承臺橋墩基礎沖刷模擬中相關模型參數設置可參考其成果，并可用于做進一步的研究。

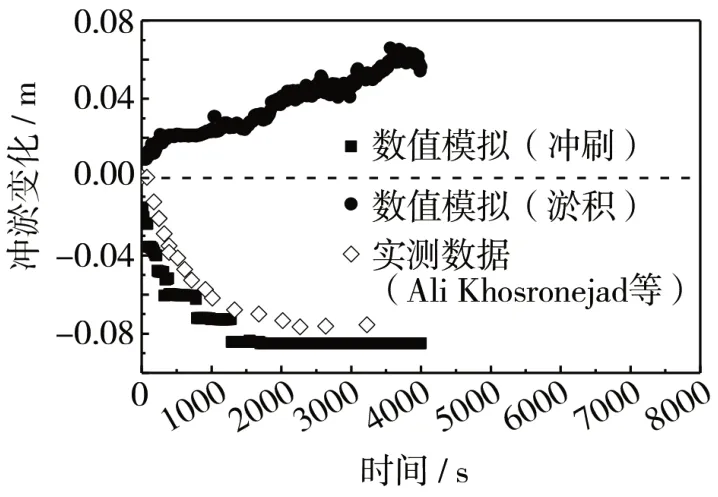
圖3 圓形橋墩局部沖淤深度變化實測結果與數值模擬對比

2 樁承臺橋墩局部沖刷特性分析

2.1 樁承臺橋墩局部沖刷理論計算

美國 HEC -18 公式推薦采用 SSC（Superposition of the Scour Components）進行樁承臺橋墩基礎局部沖刷計算。該方法分別考慮了橋梁下部結構墩身、承臺及樁基對橋墩局部沖刷深度的貢獻值，最后進行疊加計算總的局部沖刷深度。此方法物理含義明確，量綱守恒。橋墩局部沖刷計算公式為[12-13]:

式中：yspier、yspc及yspg分別為墩身、承臺、群樁樁基對橋墩局部沖刷深度的貢獻值，每部分貢獻值的計算式為：

其中：Kh（h=hpier/w/hpg）為每部分計算時相對應的修正系數；1y為起初計算來流水深（m）；y2為考慮墩身引起沖刷后水深（m ），y2=y1+yspier/2；y3為考慮了墩身和承臺沖刷后的水深為考慮了墩身和承臺沖刷后的水深，y3=y1+(yspier+yspc)/2，其他參數含義及具體計算過程參見文獻[13]。

本文以矩形承臺樁承臺橋墩基礎為例，通過美國HEC-18 公式（式（9））計算不同承臺高度條件下矩形承臺樁承臺橋墩基礎中墩身、承臺及樁基對橋墩局部沖刷深度大小及占比，進一步說明樁承臺橋墩基礎不同組成部分對局部沖刷影響特性，具體計算參數及結果見表2 與表3。

表2 矩形承臺樁承臺橋墩基礎局部沖刷計算參數（Run1）

表3 矩形承臺樁承臺橋墩基礎局部沖刷計算參數（Run2）

如表2 與表3 可知，當矩形承臺頂高程從0.09 m降低至0.06 m時，其局部沖刷深度從0.098 m增大至0.104 m，說明承臺高程降低將對局部沖刷深度有增加趨勢。同時，可以看出，隨著承臺高程降低，上部橋墩對局部沖刷的貢獻沒有變化，承臺對局部沖刷深度的貢獻增加明顯，沖刷深度貢獻占總局部沖刷深度比值從54 %增大至71 %，說明承臺在樁承臺橋墩基礎中不僅對局部沖刷深度貢獻較大，也說明承臺高程的變化也對局部沖刷深度變化有著明顯的影響。

2.2 矩形承臺樁承臺橋墩局部沖刷特性分析

如圖4 所示，以Run2 為例，當水流行至矩形承臺樁承臺橋墩迎流面，主要在承臺處形成一股上升流與一股下潛流，上升流越過承臺頂與上部橋墩作用后流向下游，這部分水流基本不對沖刷產生較大影響，而在承臺迎流面處形成的下潛水流則直接沖刷其墩前泥面，并迅速在墩前形成沖刷坑，墩前坑內流速呈中間大，兩端小分布規律。同時，水流進一步擠壓至群樁內部，形成高速水流沖刷樁群內部泥沙，在群樁內部尤其樁間距間造成較大沖刷深度。

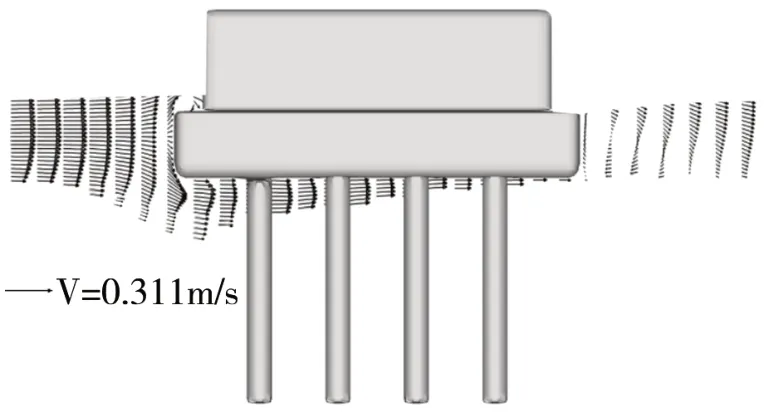
圖4 矩形承臺樁承臺橋墩基礎縱向中心斷面流速矢量分布（Run2）

如圖5 與圖6 所示，矩形承臺樁承臺橋墩基礎局部沖刷呈現前沖后淤的分布特點，最大沖刷大致位于承臺下第一排樁與第二排樁附近，墩后形成落淤區沙脊，這是因為馬蹄形旋渦具有同時向上游和下游發展的趨勢，所以沖刷坑也會沿著群樁基礎側壁同時向上游和下游發展，而且沖刷向上游發展很快，向下游發展較慢，沖刷達到極限狀態后，群樁基礎周圍的極限沖刷深度值出現在群樁基礎外側靠近迎水面處。同時，當承臺頂高程hc從0.09 m降低至0.06 m 時，其最大局部沖刷深度從0.103 m增加至0.193 m，可見承臺高程降低將對其局部沖刷深度產生明顯影響。

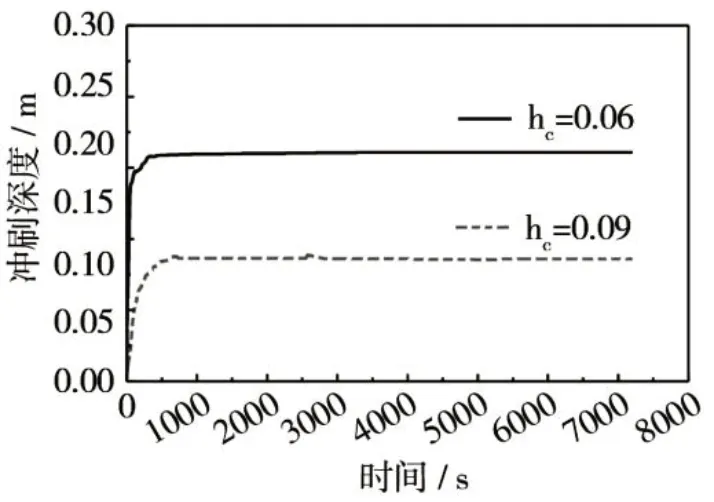
圖5 不同承臺高程矩形承臺樁承臺橋墩基礎局部沖刷深度變化

圖6 不同承臺高程梯形承臺樁承臺橋墩基礎局部沖刷深度分布示意

2.3 梯形承臺橋墩局部沖刷分析

如圖7 所示，以Run4 為例，由前述分析可知，當水流行至矩形承臺樁承臺橋墩迎流面，主要在承臺處形成一股上升流與一股下潛流，但梯形承臺由于斜坡存在使得上升水流更易爬升越過承臺頂與上部橋墩作用后流向下游，這部分水流基本不對沖刷產生較大影響，而在承臺迎流面處受到梯形承臺銳角影響，產生了更加復雜的下潛水流結構，同時，用于梯形承臺相較矩形承臺其增加了下潛水流的作用距離，使得下潛水流快速形成加速水流，并迅速在墩前形成沖刷坑，尤其梯形承臺下形成了中間小，兩端大的流速分布規律，且流速呈逆時針旋轉，更加劇了墩前沖刷坑的沖刷。同時，水流進一步擠壓至群樁內部，形成高速水流沖刷樁群內部泥沙，在群樁內部尤其樁間距間造成較大沖刷深度。

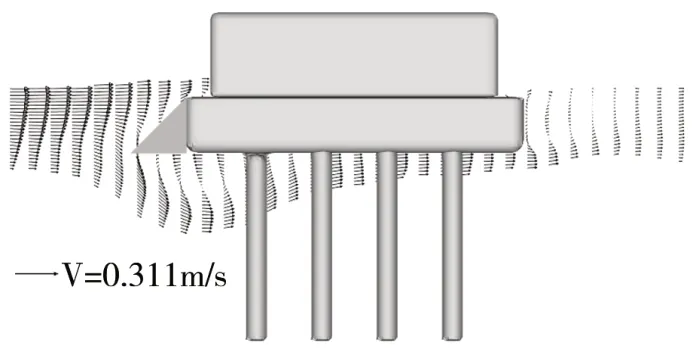
圖7 梯形承臺樁承臺橋墩基礎縱斷面流速矢量分布（Run4）

如圖8 與圖9 所示，梯形承臺樁承臺橋墩基礎局部沖刷呈現前沖后淤的分布特點，最大沖刷大致位于承臺下第一排樁與第二排樁附近，但很明顯的可以看出在群樁間距內存在一條明顯的沖刷深槽，這是由于承臺底高程較低，水流在承臺及群樁作用下，在群樁間距內形成一股較強壓縮水流造成的。同時，當承臺頂高程hc從0.09 m 降低至0.06 m 時，其最大局部沖刷深度從0.147 m 增加至0.245 m，可見承臺高程降低將對其局部沖刷深度產生明顯影響。

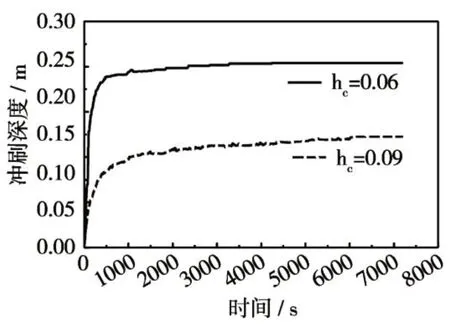
圖8 不同承臺高程梯形承臺樁承臺橋墩基礎局部沖刷深度變化

圖9 不同承臺高程梯形承臺樁承臺橋墩基礎局部沖刷深度立面圖示意

3 結語

本文通過CFD 軟件建立三維水沙動力模型研究了矩形承臺與梯形承臺樁承臺橋墩基礎在不同承臺高程條件下的局部沖刷規律，并以矩形承臺樁承臺基礎為例采用HEC-18 對其不同部分對局部沖刷貢獻進行計算，得到如下結論：

1）通過美國HEC-18 計算公式對矩形承臺樁承臺橋墩基礎不同部分沖刷貢獻值計算發現，隨著承臺高程降低，上部橋墩對局部沖刷的貢獻沒有變化，承臺對局部沖刷深度的貢獻增加明顯，沖刷深度貢獻占總局部沖刷深度比值從54 %增大至71 %，說明承臺高程的變化對局部沖刷深度變化有著明顯的影響。

2）通過建立的三維數學模型對矩形承臺與梯形承臺樁承臺橋墩基礎在不同承臺高程條件下的局部沖刷規律進行模擬發現：當承臺頂高程從0.09 m降低至0.06 m 時，其最大局部沖刷深度均發生增大。當承臺頂高程降為0.06 m 時，其擠壓水流在下部群樁間距內形成一明顯沖刷深槽，說明承臺高程變化將影響樁承臺橋墩沖刷深度及沖刷坑形態。

3）與矩形承臺樁承臺橋墩相比，梯形承臺樁承臺橋墩產生更大局部沖刷深度，其主要與梯形承臺將在墩前產生更加復雜水流結構有關，尤其受梯形承臺銳角影響，在承臺下形成了逆時針水流結構，將更加有利于對沖刷坑內泥沙進行淘刷。可見承臺高程及形狀均將影響其局部沖刷深度，因此，實際工程設計時應對承臺高程及形狀給予足夠的研究認識。