HTPB推進劑細觀損傷及載荷傳遞行為數值模擬①

逯晗斗,陳 雷,胡松啟,于慶民,3*,白帥帥,劉殊遠

(1.西北工業大學 力學與土木建筑學院,西安 710129;2.西北工業大學 航天學院,西安 710072;3.西北工業大學 航空學院,西安 710072)

0 引言

固體推進劑作為一種典型的顆粒填充復合材料,推進劑的宏觀力學性能強烈依賴于細觀結構。雖然固體推進劑類似顆粒增強復合材料,但不同的是,推進劑中的顆粒并不都是起增強作用,顆粒含量增加反而會導致材料更容易受到不可避免的破壞。目前,已有許多國內外學者采用試驗和數值的方法對推進劑在細觀尺度下的損傷進行了深入研究。VAN RAMSHORST等[1]基于掃描電子顯微鏡(SEM)研究了固體推進劑細觀形貌與宏觀變形破壞的關系,發現載荷作用下顆粒/基體界面脫粘,裂紋沿顆粒/基體界面生長。史佩等[2]基于分子動力學算法建立了具有高體積分數(60%左右)的固體推進劑顆粒填充模型,在此基礎上進行的細觀力學分析可以有效地考慮固體推進劑細觀結構對其力學性能的影響。李高春等[3]通過Mori-Tanaka方法將小顆粒和基體等效,然后模擬了大顆粒和等效基體之間的相互作用及“脫濕”損傷,得到的推進劑模量和試驗結果吻合。封濤等[4]建立了具有不同細觀結構的推進劑模型,發現大粒徑AP顆粒界面更容易脫粘,RDX顆粒的界面損傷不明顯,其含量增加會降低初始模量。張建偉等[5]根據有限元理論及細觀力學均勻化方法研究了顆粒體積分數對推進劑模量的影響,說明了填充顆粒的增強作用主要體現在瞬時模量上。LI等[6]研究了細觀結構的力學性能和推進劑中初始界面缺陷對宏觀力學影響的相關性。職世君等[7-9]通過在推進劑顆粒/基體界面處引入雙線性內聚力模型,研究了填充顆粒的含量、粒徑和位置分布等細觀特征對推進劑宏觀力學性能的影響。另外,張文普等[10]用空氣泡代替了顆粒,根據模量隨應變變化的趨勢,認為推進劑模量下降的主要影響因素是界面“脫濕”。FRANCQUEVILLE等[11]為了深入了解推進劑本構與局部損傷、宏觀力學行為之間存在的關系,通過單軸拉伸實驗,研究了推進劑應力-應變響應、體積變化,并根據受載條件下的掃描電鏡圖像,對局部損傷進行了定性描述,同時通過數值模擬討論了粘聚區參數與局部損傷萌生、演化以及粘結行為與非均質材料宏觀力學響應之間的關系。以上研究主要集中于顆粒“脫濕”這一現象的描述以及討論細觀結構、界面參數等變量對推進劑宏觀力學性能的影響,而未考慮顆粒形狀對推進劑力學性能的影響,同時缺少對顆粒和基體之間載荷傳遞能力的定量表征和分析。

為了深入了解固體推進劑細觀損傷的原因以及量化細觀結構對力學性能的影響,本文首先通過中心框增長法確定了具有一定細觀特征的推進劑的最佳RVE尺寸,并利用應力集中因子及載荷傳遞系數[12]概念,基于雙線性內聚力模型和粘超彈本構,研究了顆粒形狀、大顆粒含量以及顆粒體積分數對應力集中和載荷傳遞系數的影響,這對揭示復合固體推進劑細觀結構組成與宏觀力學行為關系、量化固體推進系統的長期可靠性至關重要。

1 HTPB推進劑各組分材料模型

固體推進劑作為一種典型的多相復合材料,其連續相基體是一種高分子聚合物,具有較好的力學性能和較小的粘度,能夠容納大量的固體顆粒;分散相由AP顆粒和Al顆粒組成,為固體推進劑提供能量;界面相發生“脫濕”是導致推進劑宏觀斷裂的主要原因。本文基于三相結構(連續相-界面相-分散相)建立了固體推進劑的細觀損傷模型。

1.1 粘超彈本構模型

HTPB固化膠片經過單軸拉伸加載和卸載試驗后,如圖1所示,完全卸載后,應變并未恢復至0,主要是由于HTPB中的大分子鏈儲存的應變勢能,使得卸載階段的斜率明顯小于初始階段,大于軟化階段。根據其力學響應,基體具有超彈性和不可恢復的粘彈特性。因此,在建立本構模型時,需要同時考慮超彈特性和粘彈特性。

圖1 加-卸載名義應力-應變實驗曲線[13]

選擇Ogden應變能函數描述推進劑基體的超彈性力學響應:

(1)

式中λi為主伸長率;μi、αi為材料參數;Dk為不可壓縮參數;J為變形后與變形前的體積比,對于不可壓縮材料,J=1。

結合式(1),可以獲得Ogden超彈性模型關于應力-應變的表達式:

(2)

廣義Maxwell模型可以表征固體推進劑靜態粘彈特性,在ABAQUS中,常用Prony級數形式來表示:

(3)

式中E∞、Ei和τi分別為平衡模量、第i個Maxwell單元的松弛模量和松弛時間;t為時間。

基于上述粘超彈性理論,Prony級數和Ogden超彈性模型的相關系數如表1和表2所示。

表1 HTPB基體松弛模量主曲線Prony級數的各階系數[14]

表2 HTPB基體3階Ogden超彈性模型[15]

1.2 分散相顆粒材料參數

固體推進劑中分散相顆粒模量及強度遠遠高于基體,準靜態加載過程中,不考慮AP和Al顆粒的損傷,將顆粒視為彈性材料[11]。Al顆粒數量巨大且粒徑較小,為了降低計算收斂難度,本文的數值模擬中僅考慮AP顆粒[16],且假定不同粒徑的AP顆粒材料參數一致,AP顆粒的彈性模量為19.5 GPa,泊松比為0.25。

1.3 雙線性內聚力模型

顆粒和基體的“脫濕”損傷是推進劑斷裂失效的主要原因,一般通過內聚力模型描述界面的損傷。其中,雙線性內聚力模型形式簡單,使用最為廣泛。在實際情況下,需要采用混合模式準則來判斷界面的損傷起始點。目前,比較常用的初始損傷準則是二次應力準則,其表達式如下:

(4)

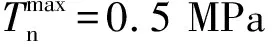
達到界面損傷起始準則后,界面開始出現損傷,損傷變量D表示為

(5)

式中D的取值范圍為[0,1],當D=0時表示界面未出現損傷,當D=1時表示界面完全失效,模擬的裂紋面完全分離。

當界面損傷開始演化時,界面剛度會隨之減小,界面剛度與損傷變量的具體關系如式(6)所示:

(6)

當界面等效位移達到0.02 mm時[17],界面完全失效。為了保證計算的收斂性,在不影響計算結果的基礎上對界面內聚力單元引入適當的粘性[18]。

2 HTPB推進劑細觀數值模型

2.1 RVE尺寸確定

細觀力學模型主要利用均勻化技術,從材料的局部本構響應來確定宏觀材料參數。均勻化技術已廣泛應用于預測材料宏觀響應的微尺度數值結果,均勻化通常是基于代表性體積單元的概念。一方面,RVE尺寸要足夠大,使其可以代表整個宏觀模型的力學性能;另一方面,RVE尺寸過大會造成計算資源極大的浪費,同時也不利于有限元計算的收斂。因此,在建模時應該考慮RVE尺寸的下界,選擇合適的RVE尺寸。

依照經驗法一般選擇最大顆粒尺寸的3～5倍[19],可選取的RVE尺寸范圍太大,且由于推進劑材料的特殊性,無法滿足一些精確計算。本節采用數值方法定量分析了RVE尺寸。為提高計算可靠性,基于目前推進劑配方,建立的模型如圖2所示,其中,模型的RVE尺寸為4000 μm×4000 μm,大顆粒(紅色)粒徑為250～425 μm,體積分數為39.94%,小顆粒(藍色)粒徑為106～150 μm,顆粒體積分數為22.7%。

圖2 RVE尺寸細觀模型

采用均勻位移邊界(后續章節有對均勻位移邊界條件的具體說明)對上述進行單軸拉伸5%。圖3是覆蓋漸增中心方框的單軸拉伸5%細觀模型應變場。如圖所示,采用中心框增長法[20]確定RVE尺寸,該方法使用從應變場中心點生長的單個方框,方框尺寸記為R,研究方框內平均應變隨方框尺寸增長的變化規律。然后通過評估平均應變在一定范圍內的收斂性來確定RVE尺寸。為了定量分析RVE尺寸,將方框內的局部平均應變記作εlocal,整個模型的全局平均應變記作εmacro,則方框內應變變化:

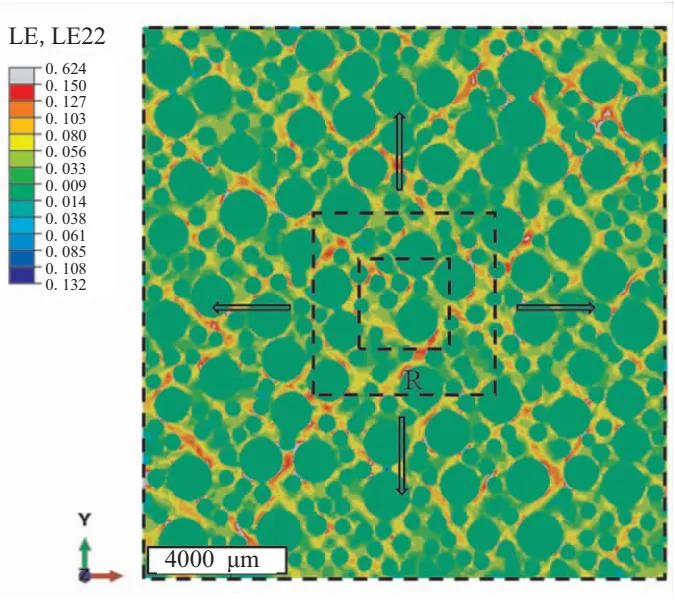
圖3 覆蓋漸增中心方框的細觀模型應變場

(7)

圖4給出了模型應變變化參數隨方框尺寸變化曲線。從圖4中可以看出,隨著方框尺寸的增大,局部平均應變接近于施加的全局應變,在較低的方框尺寸下,局部平均應變與全局應變相差較大。依據5% Strain variation和1% Strain variation將Box size劃分為3個不同的區域,分別記為Ⅰ、Ⅱ和Ⅲ。在區域Ⅰ(R<1330 μm)中,隨著方框尺寸的增大,應變變化參數呈振蕩趨勢;在區域Ⅱ(1330 μm2100 μm)中,應變參數的變化幅度小于1%,而當方框尺寸較大時,該參數依然保持在1%以下,并進一步收斂于0,因此獲得了模型的RVE尺寸為2100 μm。

圖4 平均應變隨方框尺寸的變化曲線

另外,方框尺寸增加到模型的邊界時,其平均應變變化參數有略微變大的趨勢,主要是施加的邊界條件的干擾。最后,將使用中心框增長法估算的RVE尺寸與經驗選取RVE尺寸進行比對,依據經驗一般選擇最大顆粒尺寸的3～5倍[19],RVE尺寸選取范圍過大且因推進劑材料的特殊性,無法滿足一些精確計算。如表3所示,結果較為接近,說明了采用中心框增長法估算的RVE尺寸可行性。

表3 不同方法確定RVE尺寸

2.2 邊界及載荷

圖5為均勻位移邊界條件以及周期性邊界條件。圖6為不同模型不同邊界條件下拉伸方向應力分布,給出了單顆粒模型和多顆粒模型分別在兩種邊界條件下,沿加載方向應力分布云圖。對于復雜的多顆粒模型,不同邊界條件下顆粒發生“脫濕”損傷的位置幾乎一樣,其拉伸方向的最大應力略有差別,均勻位移邊界條件下最大應力為20.972 MPa,周期邊界條件下最大應力為23.476 MPa;對于單顆粒,應力分布完全一致。

(a) Uniform displacement boundary conditions (b)Periodic boundary condition

圖6 不同模型不同邊界條件下拉伸方向應力分布

圖7為不同模型不同邊界條件應力-應變曲線。對于單顆粒模型,不同的邊界條件對應的應力-應變曲線基本吻合;而多顆粒模型中,由于顆粒脫粘的位置具有一定的隨機性,因此不同的邊界會造成一定的誤差,但仍然小于5%,可以認為兩種邊界條件不會造成計算結果較大差異。

圖7 不同模型不同邊界條件應力-應變曲線

對于擁有復雜細觀結構的推進劑而言,依賴周期性網格實現周期性邊界條件是十分困難的。因此本文選擇施加較為簡便的均勻位移邊界條件,如圖5(a)所示,僅需對模型下邊界節點和左邊界節點的豎直方向自由度和水平方向自由度分別進行約束,右邊界通過方程約束使其保持平直,同時對上邊界節點施加豎直方向位移,上邊界節點施加均勻位移載荷。

2.3 二維顆粒填充模型建立

HTPB復合固體推進劑的顆粒填充質量分數通常高達60%～80%,同時顆粒粒徑滿足一定的尺寸分布。圖8為HTPB推進劑微CT掃描重構圖、包含所有顆粒的全配方推進劑細觀模型。

(a) Real mesoscopic structure[22] (b) Filling model with small particles(Volume

從圖8(a)可以看出:AP顆粒的形狀大多接近圓形或橢圓形,在基體中高密度填充,且具有較大的尺寸跨度但大尺寸AP顆粒數量較少;Al顆粒形狀近似為圓形,其尺寸遠小于AP顆粒,且填充在AP顆粒之間,均勻分散在基體相之中;部分顆粒的邊緣及內部含有微孔洞。

常用的建立固體推進劑顆粒填充模型的方法主要有隨機吸附算法(Random Sequential Algorithm,RSA)和分子動力學(Molecular dynamics,MD)算法。另外,COLLINS等[23]基于微CT掃描,結合數學統計重構了推進劑細觀結構,該方法可以最大程度還原固體推進劑真實形貌,但普適性不好,無法對細觀結構這一變量進行討論。本文通過DIGIMAT軟件,結合真實的HTPB推進劑細觀模型,高效、準確地建立了如圖8(b)所示的推進劑細觀模型,AP顆粒粒徑采用二級配,各組分及尺寸如表4所示,粘合劑及其他助劑等效到HTPB中。將所建模型導入到ABAQUS軟件中,二維細觀顆粒填充模型視為平面應變問題進行數值求解[24],進行賦予各組分力學性能參數、有限元網格劃分、施加2.2節中圖5(a)所示的均勻位移邊界條件等前處理工作,之后開始有限元分析計算。

表4 HTPB推進劑基本配方及尺寸[21]

2.4 應力-應變均勻化

采用直接均勻化的方法,通過Abaqus-Python腳本獲取所有積分點的應力和應變,以及對應的體積或面積權重,則RVE平均應力和平均應變的分別定義為:

(8)

(9)

式中 上標t表示三角形單元,q表示四邊形單元;V為代表體積元的體積;σij、εij分別為積分點處的應力和應變;N為單元數量;Vt、Vq為單元的體積。

根據顆粒復合材料的強化機理,顆粒對基體的直接影響是通過兩者之間的載荷傳遞過程來實現的。首先,顆粒、基體和復合材料的平均應力分別為σp、σm、σc,進而定義顆粒的應力集中因子Rp=σp/σc,基體應力集中因子Rm=σm/σc,用于表征組分材料的平均應力集中程度。類似地,為了定量描述顆粒和基體之間的載荷傳遞行為,可定義載荷傳遞系數為Rp/m=σp/σm。

3 結果討論

顆粒位置的分布具有一定的隨機性,為了研究顆粒位置對計算結果的影響,結合HTPB推進劑的配方及填充顆粒尺寸分布規律,建立了4組具有不同顆粒位置分布的細觀模型,填充體積分數均為62.7%。

由于模型數量較多,僅展示了其中3個隨機模型在不同拉伸階段的剛度下降率(SDEG)云圖分布(SDEG為0表示界面未發生損傷,SDEG為1表示界面單元完全失效,并刪除失效單元),如圖9所示。可以看出,大顆粒決定了損傷最先發生的位置,從宏觀角度來看,不同模型大顆粒所占的體積分數是一致的,界面Cohesive單元包含的比例也一致,因此宏觀力學性能也幾乎一致。但是顆粒位置改變,最先失效的單元位置也隨之改變,如圖9(b)所標注的,顆粒位置的隨機導致界面單元失效的隨機性,但失效的進程并未受到影響,當外載應變為9.74%時,不同模型幾乎同時出現界面單元失效。如圖9(c)所示,當應變達到20.31%時,大部分大顆粒和極少數小顆粒都與基體發生脫粘,由于顆粒之間復雜的相互作用導致了極少數小顆粒界面“脫濕”,這進一步說明了“脫濕”損傷發生在大顆粒界面或顆粒聚集的地方,小粒徑顆粒主要起增強作用,基本不發生“脫濕”損傷。值得注意的是,顆粒位置改變雖然不會影響推進劑宏觀力學性能,但導致空穴出現的位置發生了改變,從而影響了裂紋擴展的路徑。

(a)Strain 5.33%

圖10給出了4組隨機顆粒位置模型的應力-應變曲線。可以看出,在彈性階段,應力-應變曲線完美重合,計算結果波動幾乎為0,表明在顆粒級配和體積分數相同的情況下,在“脫濕”損傷前,材料的力學性能不會受到顆粒位置改變的影響;“脫濕”損傷發生階段,應力出現下降,主要是界面單元逐漸失效,不再承受拉伸載荷,從而導致了應力曲線快速下降,由于顆粒位置不同,發生“脫濕”損傷的位置也不同,計算的結果稍有波動,但最大波動也僅5%,可以認為總體上不存在明顯的差異;當應變達到15%以后,主要是基體承載階段,應力-應變曲線逐漸匯聚靠攏。

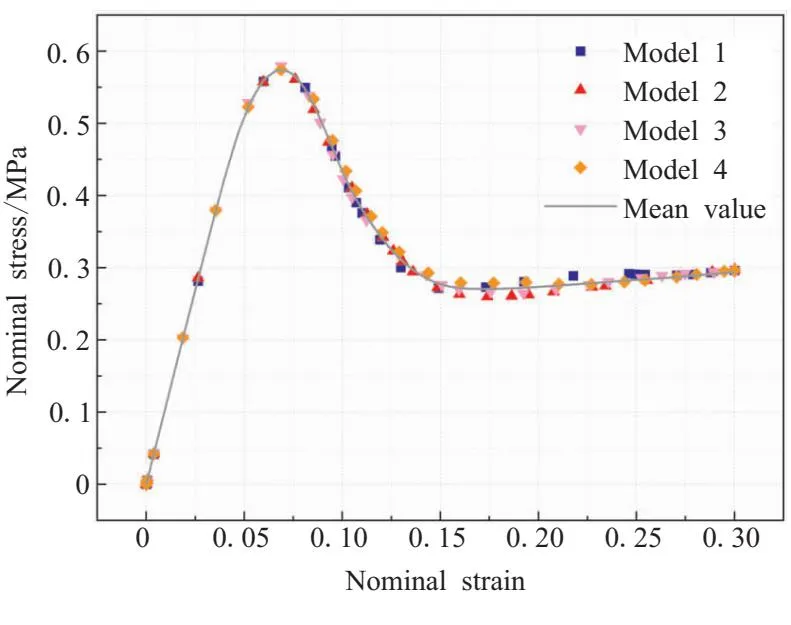
圖10 不同模型應力-應變曲線

圖11給出了隨機模型在不同加載階段的面積變化率。在彈性階段,即應變為5.33%時,不同隨機模型下面積變化率(S-S0)/S0基本一致,其中S0代表RVE模型初始面積(如圖5(a)實線方框所示),S表示拉伸變形后的面積(如圖5(a)虛線方框所示);當拉伸應變為20.31%時,顆粒位置影響了“脫濕”的位置,導致面積變化率略有差別,如Model 1面積變化率約為18.87%,Model 2的面積變化率約為18.23%,兩者的相對誤差僅為3.5%。

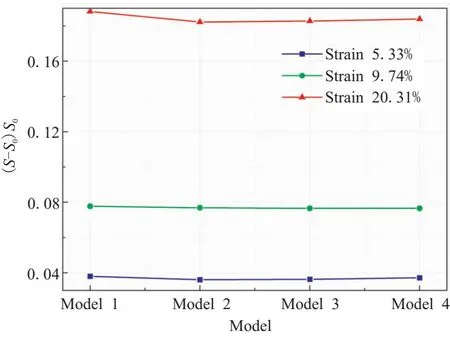
圖11 不同模型的面積變化率

由此可知,當顆粒的體積分數和顆粒級配一定時,改變顆粒的位置不會對結果產生較大影響,因此在后文的計算中可忽略顆粒位置對結果的影響。

3.1 顆粒形狀對推進劑力學性能的影響

固體推進劑的顆粒并不是理想化的圓形,麥麥提圖爾蓀等[25]對多邊形顆粒填充細觀模型進行數值計算,發現多邊形在突出的頂點附近容易產生應力集中現象,容易造成基體撕裂,因此實際生產過程中一般都會采用較為圓潤的顆粒。本節僅考慮了橢圓形顆粒,研究了相同體積分數下,顆粒的長徑比(Ap)對固體推進劑力學行為的影響,其中不同形狀的顆粒都是隨機分布的。

顆粒長徑比越大,顯然越容易發生應力集中現象。圖12(a)給出了應變為20%時,不同長徑比顆粒的最大主應力云圖分布。長徑比增加一倍,顆粒的最大拉伸主應力從1.051 MPa增加到1.209 MPa,增幅約為15%;壓縮主應力從0.16 MPa增加到0.238 MPa,增幅接近50%。對基體采用同樣的研究方法。圖12(b)給出了應變為20%時,不同長徑比基體的最大主應力分布,當長徑比Ap=1.0時,基體的最大主應力為16.679 MPa;當長徑比Ap=2.0時,最大主應力增加到了29.013 MPa,增幅約為74%。

通過載荷傳遞系數,可以有效地表征不同長徑比的顆粒載荷傳遞的效率。圖13給出了不同長徑比下,載荷傳遞系數的變化趨勢。

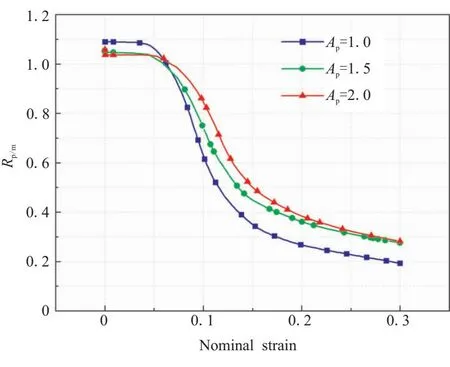
圖13 長徑比對載荷傳遞系數的影響

由圖13可以看出,在初始階段,載荷傳遞系數基本保持不變,長徑比越小,載荷傳遞系數越高,表明越圓潤的顆粒越有利于載荷傳遞;同樣的,載荷傳遞效率越高,界面單元也就越容易發生損傷。當長徑比Ap=1.0時,平均載荷傳遞系數Rp/m最先開始下降,下降速率也是最快的,主要是初始階段高效率的載荷傳遞導致界面單元失效的數量最多,界面單元失效后不再承載,從而降低了載荷傳遞效率。長徑比Ap=2.0時,初始階段載荷傳遞效率最低,但同樣卻阻止了界面單元的快速損傷,在應變大于10%以后,未失效的界面單元的數量最多,反而提高了模型的載荷傳遞效率。

3.2 顆粒級配對應力集中和載荷傳遞系數的影響

為了考慮顆粒級配對應力集中程度和載荷傳遞效率的影響,分別建立了3個不同的細觀計算模型,如圖14所示,模型體積分數都為42.7%。其中,f表示模型的體積分數,下標AP-1表示大顆粒,粒徑250～425 μm,呈正態分布;AP-2表示小顆粒,粒徑為150 μm。

(a)Model 1 (b)Model 2 (c)Model 3

加載過程中,不同級配下顆粒和基體應力集中因子的變化趨勢如圖15所示。可以看出,對于顆粒來說,其應力集中因子Rp在加載的最初階段基本保持不變,而后下降速率開始增大,最后下降速率又開始變緩。基體的應力集中因子Rm的變化趨勢與顆粒正好相反,即加載的最初階段基本保持不變,而后上升速率開始增大,最后上升速率又開始變緩。同時,大顆粒含量越高,在初始階段顆粒的應力集中程度越大,脫粘后顆粒的應力集中程度越小;初始階段基體的應力集中程度越小,脫粘后基體的應力集中程度越大。以全是大顆粒的模型為例,隨著“脫濕”的進行,顆粒的應力集中因子先下降,而后趨于平穩,整體下降的速率逐漸增加而后逐漸減慢,最后顆粒應力集中因子趨于0,表明此時基體的應力幾乎無法傳遞到顆粒中,整個模型的平均應力基本上和基體等效。

圖15 不同級配對應力集中因子的影響

圖16給出了不同顆粒級配下,載荷傳遞系數的變化關系。在初始階段,載荷傳遞系數不會隨外加載荷的變化發生改變,大顆粒體積分數從0增加至42.7%時,載荷傳遞系數也從0.95增加至1.25,表明初始階段大顆粒含量增加可以提高載荷傳遞效率;隨著應變的增加,僅含大顆粒模型的載荷傳遞系數開始迅速減小,而不含大顆粒模型的載荷傳遞系數變化不大。載荷傳遞系數下降主要原因是界面單元損傷發生失效從而無法傳遞載荷,表明大顆粒含量越多,其界面損傷的進程越快,同時界面損傷程度越劇烈,大顆粒更容易脫粘,脫粘以后載荷傳遞比較困難,所以曲線下降更快;隨著拉伸應變的進一步增加,載荷傳遞系數進入平緩下降階段,當應變為0.3時,僅含有大顆粒模型的載荷傳遞系數接近0,表明大顆粒/基體界面大部分單元均已失效不再承載,大顆粒含量越高,界面“脫濕”損傷也越嚴重。

圖16 不同級配對載荷傳遞系數的影響

3.3 顆粒體積分數對應力集中和載荷傳遞系數的影響

針對顆粒體積分數對復合材料內部載荷傳遞行為的影響,以顆粒長徑比為1.0的情況為例進行研究。結合推進劑顆粒級配關系,生成3組不同體積分數的推進劑細觀填充模型,模型對應的體積分數分別為22.7%、42.7%和62.7%,如圖17所示。

(a)fAP=22.7% (b)fAP=42.7% (c)fAP=62.7%

不同顆粒含量時,顆粒和基體應力集中因子隨外加應變的變化規律如圖18所示。從圖中可以看出,“脫濕”前顆粒和基體的應力集中因子差距較小,都在1.0附近;當應變達到0.1后,隨著顆粒含量的提高,顆粒和基體的應力集中因子都將逐漸增加,這是因為顆粒體積分數的變化,會在較大程度上改變復合材料的平均應力。以應變為30%的階段為例進行分析,當顆粒體積分數很小時,顆粒的應力集中因子也很小,如圖體積分數為22.7%時,顆粒的應力集中因子接近0,復合材料的平均應力將會更接近于基體的平均應力,同時基體的應力集中因子也將更接近于1.0;而當顆粒體積分數很大時,復合材料的平均應力將更接近于顆粒,因此顆粒的應力集中因子將趨近于0.5,而同時基體的應力集中因子接近2.0。

圖18 不同體積分數對應力集中因子的影響

體積分數對載荷傳遞系數的影響如圖19所示。在初始階段,顆粒體積分數越大,載荷傳遞系數越小,表明初始階段體積分數增加會降低載荷傳遞的效率;當拉伸應變約0.05時,載荷傳遞系數開始下降,和改變顆粒級配不同的是,體積分數發生改變,并不會影響損傷的進程,載荷傳遞系數幾乎同時下降,但會影響其下降的速率。體積分數fAP=22.7%的載荷傳遞系數下降最快,下降幅度最大,當應變達到30%時,載荷傳遞系數從初始1.2下降至0,表明此時界面損傷嚴重,應力無法通過基體傳遞顆粒;而當體積分數fAP=62.7%時,載荷傳遞系數最大值和最小值的差值明顯小于較低體積分數的情況。在基體承載階段,體積分數越低,其載荷傳遞系數的變化越平緩,主要是因為體積分數越低,界面相的占比也就越少,當大部分單元發生“脫濕”損傷后,阻止了顆粒和基體之間的載荷傳遞,此時顆粒的平均應力接近0,RVE模型的平均應力和基體的平均應力接近。

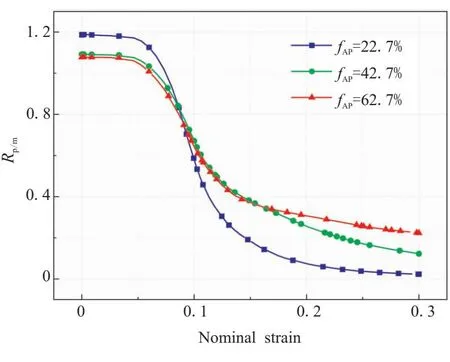
圖19 不同體積分數對載荷傳遞系數的影響

4 結論

本文基于粘超彈性本構和雙線性內聚力模型對HTPB固體推進劑進行了數值模擬,研究了推進劑細觀損傷和載荷傳遞特性,得到以下結論:

(1)相較于經驗法,采用中心框增長法確定的RVE尺寸更為精確、合理;顆粒位置隨機并不會對RVE模型的力學性能造成明顯的影響,這也進一步驗證了采用RVE模型來代表宏觀推進劑的可靠性,但會改變空穴出現的位置,從而影響了裂紋擴展的路徑。

(2)顆粒的長徑比越大,初始階段載荷傳遞效率越低,從而阻止了界面單元的快速損傷;相同體積分數下,由于大顆粒的界面處更容易發生“脫濕”損傷,隨著載荷的增加,推進劑的應力值及載荷傳遞系數下降得更快。

(3)體積分數發生改變,并不會影響損傷的進程,但會影響載荷傳遞系數下降的速率;顆粒填充體積分數主要影響著推進劑基體的承載能力,顆粒的體積分數越低,相應基體的占比則越大,在“脫濕”后,RVE平均應力就越接近基體的平均應力。

致謝：本研究得到了173計劃基金(2021-JCJQ-JJ-0401)、中央高校基本科研業務費(D5000210602)及西安近代化學研究所創新合作項目(SYJJ200313)等資助,在此表示感謝!