基于改進自適應擴展卡爾曼濾波的高精度姿態解算

吳葉麗,行鴻彥,侯天浩,王海峰,李 瑾

(南京信息工程大學電子與信息工程學院,江蘇 南京 210044)

0 引言

高精度姿態角度解算對移動目標自主定位導航有著重要的應用價值[1-3]。姿態角度可以通過陀螺儀傳感器[4]的積分得到,但是所測數據在長時間積分環境下容易產生累積誤差,單個的傳感器采集到的數據信息較為單一,不具有可靠性,并且進行姿態解算的過程中,傳感器采集的數據中會存在不確定性的系統噪聲和測量噪聲,導致得到的位姿結果產生較大的偏差。而采用陀螺儀傳感器、加速度傳感器和地磁計對姿態變換情況共同進行跟蹤可有效解決上述問題,確保采集的數據具有充分性和可靠性,通過將三個傳感器的數據進行信息融合,實現較為準確的姿態估算。

國內外學者對多個應用背景下的姿態解算進行了大量研究[5-7]。文獻[8]提出一種結合共軛梯度法和互補濾波的混合濾波算法,實現慣性傳感器的姿態解算,但沒有充分考慮傳感器數據的影響、算法迭代復雜且計算量較大。文獻[9]通過對多個慣性傳感器進行空間陣列布局,并設計了基于BP神經網絡的誤差補償模型,減少姿態的誤差,一定程度上提高了姿態解算的準確性,但該方法姿態解算過程中增加了較多計算參數,解算實現步驟較為復雜。文獻[10]提出了一種基于優化自適應無跡卡爾曼濾波的姿態解算方法,通過對陀螺儀數據和加速度數據進行誤差預處理,再通過所提算法實現姿態角度解算,但在濾波過程中沒有考慮誤差的迭代更新過程。文獻[11]提出了一種基于Q學習的方法,可以自動調整過程和測量噪聲協方差矩陣的值,解決了迭代過程中的誤差影響,降低了姿態解算誤差,但同時更新過程和測量噪聲協方差矩陣和容易造成姿態發散且計算量增加。文獻[12]將互補濾波器與EKF算法相結合,提出了一種改進的EKF濾波算法實現對無人機的姿態解算,一定程度上提高了精度和實時性,但是該方法需要進行兩步濾波過程,計算量大且容易導致結果發散,仍需要對解算精度進行提高。

為解決已有方法的姿態解算精度較低和計算復雜等問題,本文通過設置權重值對測量噪聲協方差矩陣R的估計公式進行改進,提出一種改進加權自適應的擴展卡爾曼濾波算法應用于姿態解算。

1 優化自適應的擴展卡爾曼濾波算法

傳統的EKF模型要求過程噪聲和測量噪聲的均值為零且統計特性已知的白噪聲。但在動態實踐中無法滿足上述要求,也無法準確地對噪聲的統計特性進行描述。Sage-Husa自適應濾波方法可有效顧及實際過程中的測量信息和動態信息,可以不以動力學模型噪聲先驗協方差矩陣為基礎,就能估計出狀態向量和測量向量的協方差矩陣,可有效進行濾波。

1.1 Sage-Husa自適應濾波算法

Sage-Husa濾波利用開窗法估計出此刻的測量噪聲協方差矩陣或過程噪聲協方差矩陣,使過程噪聲協方差矩陣和測量噪聲協方差矩陣自適應于此時的狀態信息和測量信息,結合EKF濾波進行解算,進而獲得最優的狀態估計值。

EKF的非線性系統表達式為

(1)

對于非線性的EKF系統線性化后其系統方程為

(2)

式(2)中,X(k)為狀態向量;Z(k)為觀測向量;A為狀態轉移矩陣,是狀態向量非線性函數泰勒級數展開式的一階項;H為觀測矩陣;w(k)為過程噪聲;v(k)為測量噪聲。

由上,基于Sage-Husa的時變噪聲統計估計器[13]為

q(k)=(1-d(k))q(k-1)+
d(k)(X(k|k)-AX(k-1|k-1)),

(3)

Q(k)=(1-d(k))Q(k-1)+d(k)(K(k)ε(k)·
ε(k)TK(k)T+P(k|k)-AP(k-1|k-1)AT),

(4)

r(k)=(1-d(k))r(k-1)+d(k)(Z(k)-
HX(k|k-1)),

(5)

R(k)=(1-d(k))R(k-1)+d(k)(ε(k)ε(k)T-
HP(k|k-1)HT),

(6)

但傳統的Sage-Husa自適應濾波方法存在一些缺點:

1) 由文獻[14]可知,在實踐過程中不能同時估計出系統中的Q和R,只能在一方已知的條件下,估計出另一個;

2) 由式(3)-式(6)可知,d(k)和b的數值選取,直接影響了系統的自適應程度,傳統的Sage-Husa自適應方法,使用單一的d(k)數值對不同傳感器測得的數據進行噪聲估計,不能滿足實際的要求,容易產生較大的誤差;

3) 由式(4)、式(6)可知,系統的噪聲方差矩陣Q或R可能失去半正定性和正定性發生濾波發散,導致系統不具有穩定性和收斂性。因此,本文需要針對上述問題對傳統的Sage-Husa自適應濾波方法進行改進。

1.2 優化加權自適應的擴展卡爾曼濾波算法

針對在實踐過程中不能同時估計出系統中的Q和R的問題,本文實現姿態解算的系統的過程噪聲較小并且變化較為穩定,而噪聲通常受到復雜的環境影響,使得實際過程中的測量噪聲會發生較大的變化。因此,本文僅對系統的測量噪聲協方差R進行估計,對過程噪聲協方差矩陣Q設置為已知定值,并且對測量噪聲協方差矩陣進行改進,提高系統的穩定性和準確性。由此,本文提出一種改進的加權Sage-Husa自適應擴展卡爾曼濾波算法。算法流程如下:

狀態預測方程:

X(k|k-1)=f(X(k-1|k-1))。

(7)

預測協方差方程:

P(k|k-1)=AP(k-1|k-1)AT+Q。

(8)

更新增益方程:

K(k)=P(k|k-1)HT[HP(k|k-1)HT+R]-1。

(9)

計算殘差:

e(k)=Z(k)-g(X(k|k-1))。

(10)

更新狀態估計方程:

X(k|k)=X(k|k-1)+K(k)e(k)。

(11)

更新協方差矩陣方程:

P(k|k)=(I-K(k)H)P(k|k-1)。

(12)

對不同的傳感器的噪聲統計特性的置信程度進行判斷,對不同傳感器測量所得的數據賦不同的權重值,可以有效解決單一的d(k)數值對不同傳感器測得的數據進行噪聲估計而導致產生誤差的問題。

濾波出現收斂趨勢時,誤差協方差矩陣P逐漸減小至0,可忽略不計,對傳統的測量噪聲協方差矩陣R的估計公式進行改進,保留殘差e(k),同時使其滿足傳統R的變化趨勢,保證了矩陣R的正定性,防止發生濾波發散的情況,使R隨著噪聲和系統真實情況的變換進行估計。

改進的加權測量噪聲協方差矩陣更新方程:

R(k)=(I-w(k)D(k))R(k-1)+w(k)D(k)·
|((I-HK(k-1))e(k)e(k)T(I-HK(k-1))T)|,

(13)

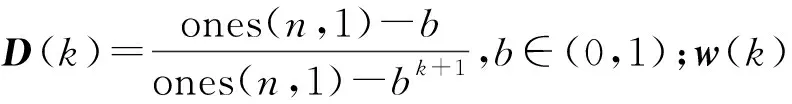
綜上所述,改進算法結構簡單、計算效率高、穩定性好、靈活性高,更適用于系統求解姿態角度信息。

2 基于優化加權自適應擴展卡爾曼濾波的姿態解算

姿態角一般由陀螺儀、加速度計傳感器的測量數據解算得到[15],陀螺儀可由所測角速度經積分得到三個姿態角:俯仰角、航向角和橫滾角,其不易受到外界環境的干擾,且短時內的測量值較為準確但單一的陀螺儀測得數據在長時間積分環境下容易產生累積誤差,而加速度計和磁力計長時間測量的數據比較穩定、準確。因此,本文利用提出的WAEKF方法將陀螺儀、加速度計和地磁計的測量數據進行了融合,實現對陀螺儀實踐過程中產生的隨機偏移誤差的修正,在EKF算法的基礎上,加入自適應過程,控制系統的殘差矩陣對系統的影響,進而得到姿態角的最優估計。其實現原理如圖1所示。

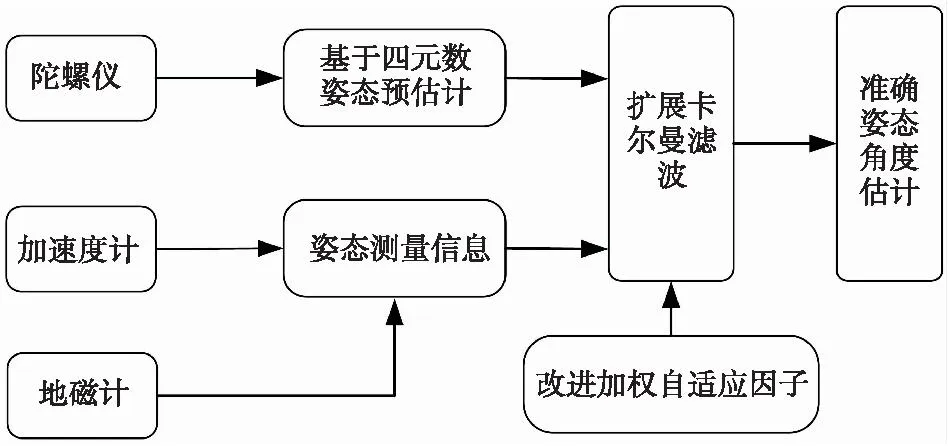
圖1 基于改進方法的姿態角度估計原理圖Fig.1 Schematic diagram of attitude angle estimation based on the improved method

2.1 基于慣性導航的姿態解算原理

姿態解算的方法主要有歐拉法、方向余弦法和四元數法等。歐拉法的計算速度較慢,并且計算過程中矩陣會產生“奇點”,造成萬向節死鎖的現象[16],實時計算困難,難以用于實踐。方向余弦法可有效避免歐拉法出現的“奇點”現象,但計算量較大、較為復雜。因此本文在姿態融合過程中使用四元數法,可克服歐拉法的缺點并且方法簡單、計算量較小。最終將四元數轉換為歐拉角,得到姿態角信息。

若載體坐標系為B系,地理坐標系為N系,兩者可通過旋轉矩陣進行轉換,由四元數表示的從地理坐標系旋轉到載體坐標系的旋轉矩陣[17]為

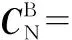
(14)

則由旋轉矩陣解算出目標載體的歐拉角,即俯仰角γ、橫滾角θ和航向角φ為

(15)

2.2 基于慣導和改進方法的姿態解算

基于慣導系統和四元數法構建狀態方程和測量方程,將四元數和陀螺儀角速度偏移量作為狀態方程的變量,將加速度計和地磁計測得的數據作為測量信息,加入自適應因子考慮系統的測量噪聲對系統精度的影響,提高系統姿態角最優估計的準確性。

2.2.1建立狀態方程

使用一階龍格-庫塔法對陀螺儀的角速度值進行更新處理,實現四元數值的更新,則由龍格-庫塔法得到的離散模型[18]為

(16)

式(16)中,q(k),q(k-1)分別為k,k-1時刻的四元數;T為系統采樣時間間隔;ΩB為載體坐標系相對于地理坐標系的角速度在載體坐標系上的分量。

陀螺儀的偏移量模型可表示為

(18)

則,以四元數和陀螺儀數據偏移量作為狀態變量,進而建立的狀態方程為

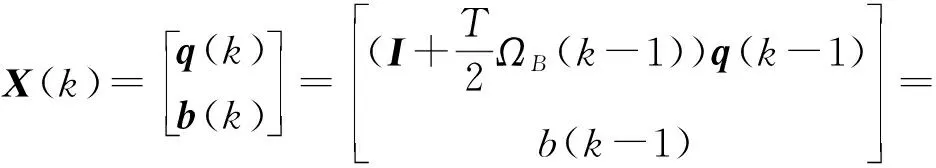
(19)

2.2.2建立測量方程

本文將加速度計和地磁計得到的數據作為測量方程,對狀態向量實現補償估計,設加速度計數據為aB,地磁計所測數據為mB,與地理坐標系中的加速度和磁場mN關系[19]可表示為

(20)

通過地磁和加速度計解算所得的姿態角經過求解得到初始四元數的數值,進而實現四元數的更新優化,由式(20)求解可得由地磁計和加速度計數值表示的姿態角的表達方式為

(21)

選取加速度計和地磁計的數據向量作為測量信息,因此本系統的測量方程表達式為

(22)

2.2.3姿態估計的實現步驟

本文改進WAEKF方法可以更新時變噪聲矩陣參數R,因此,通過本文方法實現姿態角度解算,可有效解決姿態解算過程中的誤差累積問題,提高姿態解算精度。將地磁計的測量數據、加速度傳感器的測量數據和陀螺儀傳感器的測量數據經本文方法解算處理后,得到最優姿態。

算法具體的實現步驟如下:

1) 建立系統的狀態方程(19)和測量方程(22),并對系統進行初始化設置;

2) 根據式(7)、式(8)實現時間更新,得到預測狀態變量X(k|k-1)和預測協方差矩陣P(k|k-1);

3) 根據式(9)更新濾波增益,利用增益K(k)更新k時刻的最優狀態估計X(k|k)和協方差矩陣P(k|k);

4) 重復上述步驟2)至3),實現四元數的最優估計,得到最優姿態角度信息。

本文算法通過使用改進的噪聲統計估計器,能夠有效避免濾波發散,并且能夠實時地估計和修正系統的量測噪聲,實現系統的最優估計。

3 實驗與結果分析

基于MPU9250搭建移動小車實驗平臺,將慣性傳感器在二維水平面內進行移動,利用算法實現移動小車的姿態融合解算,獲取更加準確的姿態信息。基于本文的WAEKF方法實現陀螺儀數據、加速度數據和地磁計數據的姿態解算,并將實驗的解算結果與傳統AEKF、EM-AEKF和互補濾波方法進行對比分析,驗證本文方法求解姿態角具有優越性。

為直觀體現改進方法的姿態解算實驗效果,本文選取均方根誤差(root mean square error,RMSE)和平均絕對誤差(mean absolute error,MAE)對姿態角度誤差情況進行衡量評估[20]。RMSE和MAE表達式如下:

(23)

(24)

式(23)、式(24)中,N表示所測數據個數,x(t)表示系統的解算估計值,y(t)表示系統的真實數據。RMSE可以反映出數據值與真實值之間的擬合程度,RMSE的值越小,表明處理后的實驗數據具有更高的精確性。MAE可凸顯實驗值與真實值之間的數值差距,通過將所有的誤差絕對值相加,可以有效避免因數據值比真實值局部過高或過低而抵銷誤差,因此較適合用于評估數據的整體誤差。

3.1 與傳統AEKF算法的誤差對比

將慣性傳感器在二維水平面內進行直線運動。使用AEKF濾波器和本文的WAEKF方法對慣性測量單元數據進行處理,并將實驗的解算誤差結果進行比較分析,采樣周期為0.02 s。

3.1.1傳統自適應擴展卡爾曼濾波的角度解算誤差實驗分析

采用基于傳統的Sage-Husa自適應擴展卡爾曼濾波算法對傳感器的數據進行融合,分別得到俯仰角、航向角和橫滾角的姿態角度信息,并將其與真實值之間的誤差情況進行表現,顯示出傳統算法的融合效果,效果如圖2所示。

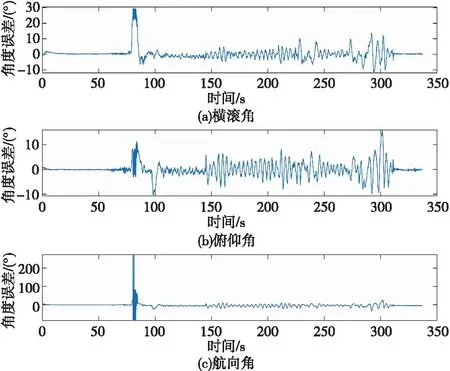
圖2 基于AEKF姿態解算角度誤差曲線Fig.2 Angle error curve calculated based on AEKF attitude

由圖2可看出,基于AEKF的姿態解算結果存在較大誤差值。解算的橫滾角誤差極值差約為40°,在數列值為85 s附近出現誤差極大值,高出真實值33°,誤差變化較為明顯。基于AEKF姿態解算的俯仰角誤差波動幅度值約為28°,誤差極大值高出實際值18°,誤差變化分布的較為明顯。基于AEKF解算的航向角的誤差值在75～85 s區間外整體變化較為平穩,但在75～85 s區間內出現了異常尖峰誤差,誤差極值大于200°,對解算結果造成了較大影響。因此,傳統的AEKF對慣性傳感器數據進行濾波解算后,姿態角度的誤差變化情況都較為明顯,誤差值變化區間較大并且都出現了一段異常尖峰值,因此仍需要對傳統的AEKF濾波算法進行改進。

3.1.2優化加權自適應擴展卡爾曼濾波的角度解算誤差實驗分析

在吸收Sage-Husa濾波和基于傳感器置信程度進行加權的基礎上,本文提出一種新的WAEKF方法,用于改善傳統的AEKF濾波算法的不足,增加濾波融合的靈活性和有效性。

由圖3可知,基于WAEKF方法解算的姿態角誤差明顯小于AEKF的姿態解算結果,能夠更加準確、有效地實現姿態解算。WAEKF方法解算的橫滾角的誤差整體變化較為平緩,無異常尖峰值段,相較于AEKF算法的誤差變化范圍減小約33°,橫滾角誤差變化程度有所控制。本文方法解算的俯仰角誤差波動幅度值約為13°,誤差極大值高出實際值8°,相較于AEKF算法誤差極大值減小約10°。基于本文方法得到的航向角誤差波動幅度值約為13°,遠小于基于AEKF算法的航向角誤差數值范圍,并且整體誤差值偏小。

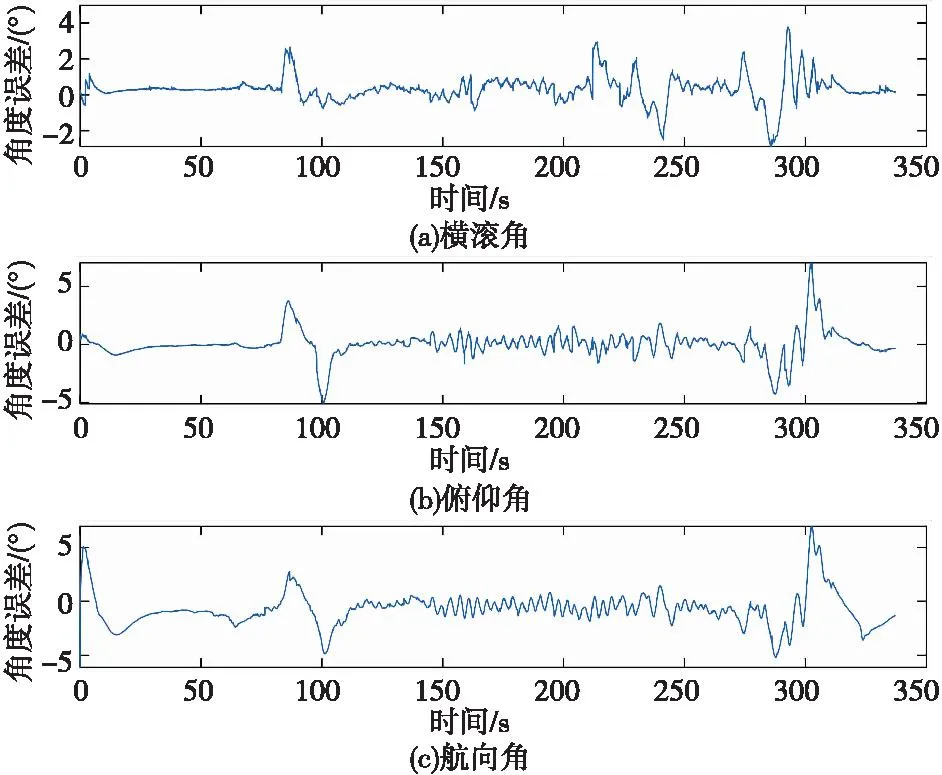
圖3 基于WAEKF姿態解算角度誤差曲線Fig.3 Angle error curve calculated based on WAEKF attitude

因此,基于WAEKF方法解算的姿態角度信息相較于傳統的AEKF算法的解算結果得到了有效地改善,尤其是航向角角度值變化更加準確,說明基于WAEKF方法的姿態解能夠依靠改進的測量噪聲協方差矩陣自適應濾除噪聲,減小誤差,提高姿態解算精度。

3.2 姿態角度對比分析

為證明本文方法對姿態角度解算具有高效性,將慣性傳感器在二維水平面內進行直線運動。利用互補濾波、基于EM-AEKF和本文的WAEKF方法分別對傳感器數據進行處理,直觀對比不同方法融合得到的角度變化情況,結果如圖4-圖6所示。w(k)取(0.5,0.95,0.95,0.95,0.99,0.99)。

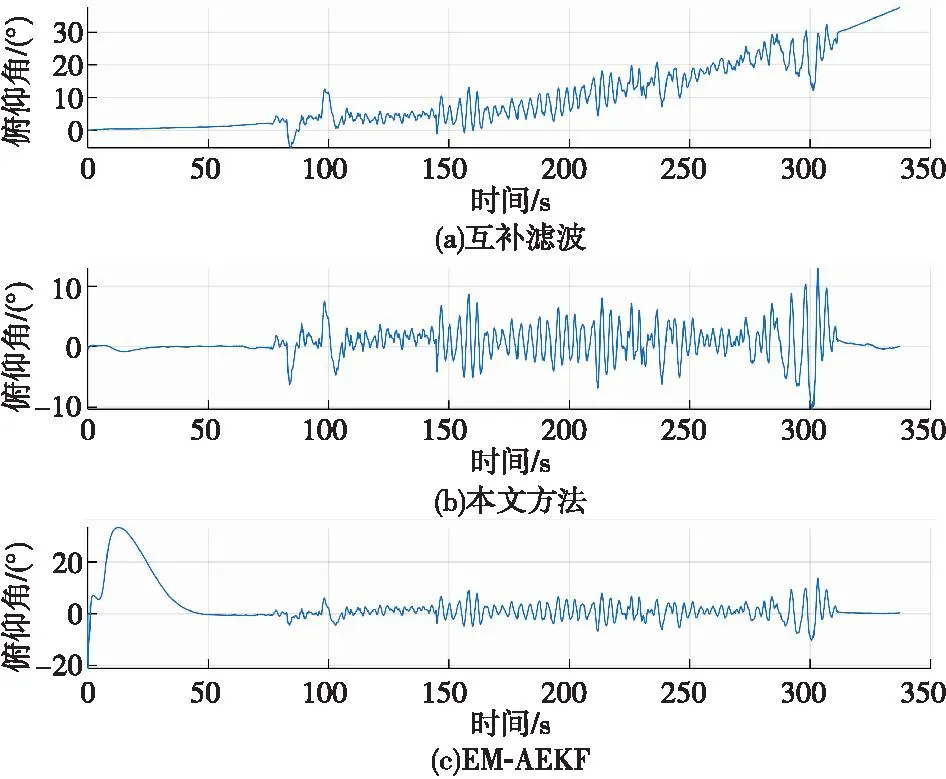
圖4 不同方法解算的俯仰角角度變化圖Fig.4 Elevation angle variation figure calculated by different methods

由圖4可知,互補濾波方法解算后在時間序列200 s后得到的俯仰角隨著時間的推移,信號發生嚴重漂移,誤差逐漸增大,因此互補濾波方法較不適合俯仰角的融合解算。基于EM-AEKF方法解算的俯仰角在時間序列為0～50 s內誤差較大,誤差波動幅度值約為30°,因此該方法解算的俯仰角誤差依然較大。基于WAEKF方法融合解算后的俯仰角整體波動最為平緩,誤差值相較于互補濾波和基于EM-AEKF方法最小。

由圖5可知,基于互補濾波方法解算的橫滾角在時間為100 s后逐漸下降低至-55°,互補濾波方法解算的橫滾角誤差較大。基于EM-AEKF方法解算的橫滾角在時間為0～50 s內誤差較大,誤差極值約為-50°左右,且隨著時間的增加,橫滾角波動較為明顯,因此該方法解算的橫滾角存在明顯失真。基于WAEKF方法解算的橫滾角整體波動穩定,誤差波動幅度值約為20°,解算的橫滾角誤差遠小于互補濾波和EM-AEKF方法。

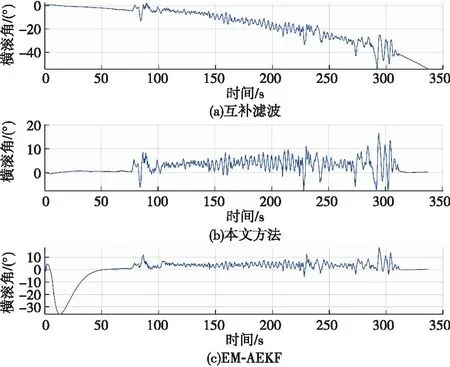
圖5 不同方法解算的橫滾角角度變化圖Fig.5 Changes of roll angle calculated by different methods

由圖6可知,基于互補濾波方法在整個時間序列內解算得到航向角的波形呈上升趨勢,隨著數據的疊加,誤差逐漸增大,最大值偏離40°,因此互補濾波方法較為不適合本文數據下的航向角融合。基于EM-AEKF方法解算的航向角整體變化較為穩定,但0～8 s之間存在較大異常值,因此該方法仍待改進。基于WAEKF方法解算得到的航向角角度值在-109°～-94°之間,解算的航向角誤差相對最小,角度變化具有穩定性和準確性,因此可以用于實際應用中求解航向角。

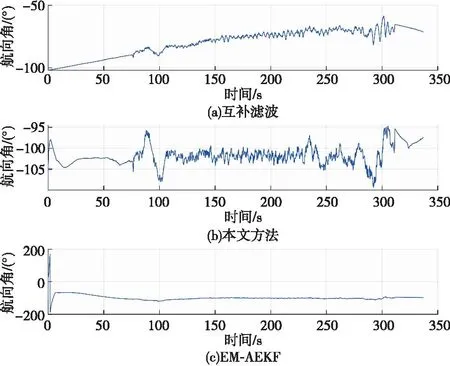
圖6 不同方法解算的航向角角度變化圖Fig.6 Variation of course angle calculated by different methods

綜上所述,基于互補濾波方法解算的俯仰角、橫滾角和航向角都存在明顯的漂移現象;基于EM-AEKF方法解算的俯仰角、橫滾角和航向角都存在較大的異常值。本文的WAEKF方法可有效解決互補濾波方法姿態解算存在漂移和EM-AEKF方法姿態解算存在異常值導致誤差較大的問題,WAEKF方法解算的俯仰角、橫滾角和航向角波形變化都較為平穩且誤差較小,能夠提高姿態解算精度,較適用于實踐應用。因此,WAEKF方法具有優勢性和準確性。

本文為對比四種方法下姿態角的解算效果,使用MAE對其誤差進行衡量,并通過記錄計算時間衡量四種方法的實現效率,結果如表1所示。

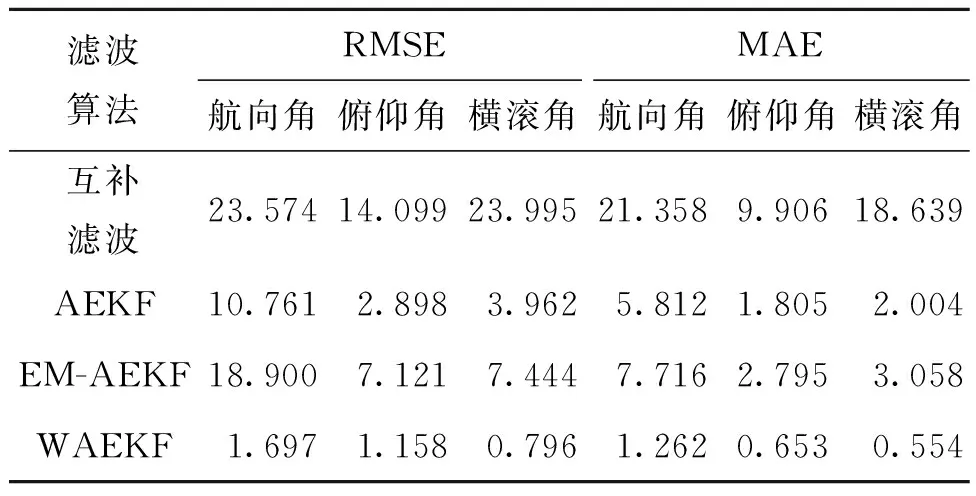
表1 不同方法航向角解算誤差對比表Tab.1 Comparison table of heading angle calculation errors of different methods

從表1可知,本文的WAEKF方法解算得到的橫滾角的RMSE和MAE值明顯小于其他三種方法,EM-AEKF和互補濾波方法解算的橫滾角誤差較大。WAEKF方法解算的俯仰角的RMSE和MAE明顯小于EM-AEKF和互補濾波方法,略小于AEKF方法。基于WAEKF方法解算得到的航向角的RMSE和MAE值明顯小于其他三種方法,且相較于AEKF方法,解算得到的航向角的RMSE和MAE分別降低了84.23%,78.28%。

因此,本文的WAEKF方法相較于互補濾波、AEKF和EM-AEKF方法的姿態解算效果最好,誤差最小,能夠自適應濾除噪聲影響,姿態解算精度最高。

為驗證本文方法的姿態解算具有適用性,在上述相同實驗條件下,將慣性傳感器在水平二維平面內進行多角度變化運動,由于本文主要考慮載體在二維水平面內的移動,此時只有航向角發生顯著變化,不同方法下的航向角解算結果如圖7所示。

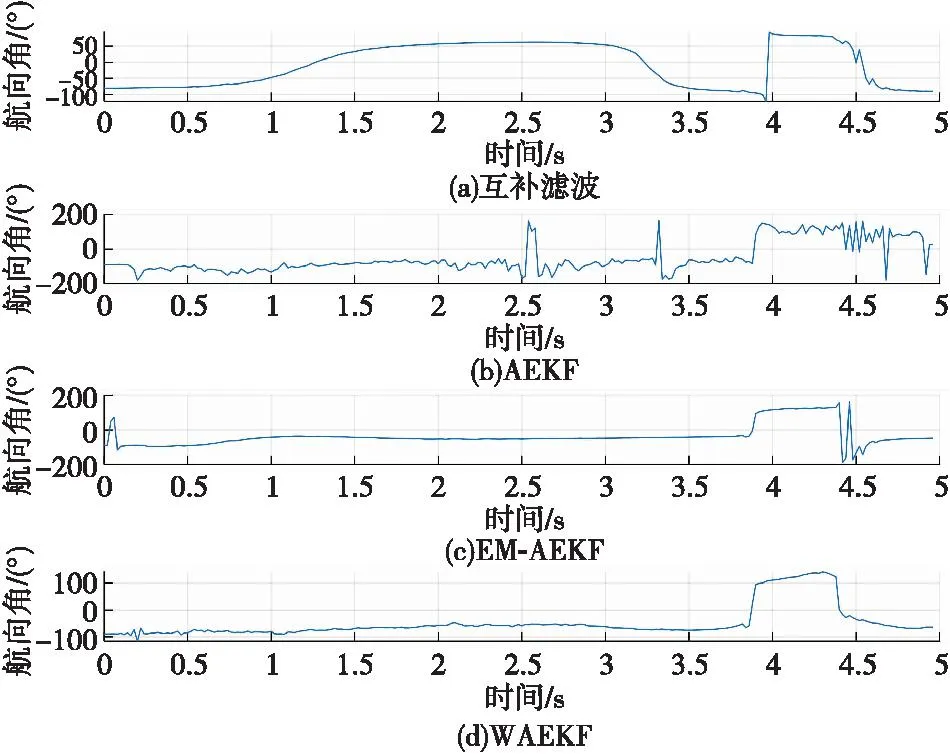
圖7 多角度變化運動下航向角對比圖Fig.7 Comparison of heading angles under multi angle changing motion

由圖7可知,基于互補濾波方法解算的航向角誤差最大,發生明顯漂移。AEKF解算的航向角存在尖峰值,并且在4.4 s后解算的航向角存在明顯漂移誤差。基于EM-AEKF方法和本文的WAEKF方法解算的航向角值較為接近真實值,但在0.5～3.85 s之間,基于EM-AEKF方法解算的航向角略小于真實值,且波形存在異常尖峰值。基于WAEKF方法解算在多角度變化運動背景下解算航向角的效果最佳,解算的航向角波形變化平穩且不存在異常尖峰值,同樣克服了互補濾波、AEKF及EM-AEKF方法解算的航向角存在異常尖峰和漂移等問題,在多角度變化運動背景下同樣適用。

綜上所述,可知基于WAEKF方法姿態解算精度整體優于其他三種方法,姿態解算時能夠自適應濾除噪聲影響,解算角度精度較高,具有優越性和可行性。

4 結論

本文對測量噪聲協方差矩陣的估計公式進行了改進,設置權重值對測量噪聲協方差矩陣進行調節,提出一種基于優化加權自適應的擴展卡爾曼濾波方法實現姿態解算,解決了濾波發散的問題,提高姿態角度解算的精度。利用本文方法實現慣性傳感器測量數據的姿態解算,驗證本文方法的有效性,對陀螺儀數據采用基于四元數的龍格-庫塔法求得姿態運動模型,建立狀態方程,將地磁計和加速度計的數據作為測量信息,利用優化加權的自適應因子調節測量噪聲協方差矩陣,控制測量殘差的影響,經過不斷遞歸更新能夠自適應濾除測量噪聲,估算出最優的姿態角。實驗表明,相較于傳統的自適應擴展卡爾曼濾波算法,本文方法解算姿態的誤差得到了較大的改善。