不同曲線半徑下軌底坡與輪徑差最佳匹配研究

朱愛華,孟宇軒,張 帆,楊建偉,郭宇軒

(北京建筑大學(xué) 城市軌道交通車輛服役性能保障北京市重點(diǎn)實(shí)驗(yàn)室,北京 100044)

軌底坡是軌道的重要參數(shù),軌底坡存在誤差或設(shè)置不合理會影響車輛動力學(xué)性能,也會對車輛和鋼軌造成不同程度的損傷。輪徑差屬于車輪損傷的一種類型,不僅影響車輛的動力學(xué)性能,還會使車輪踏面磨耗現(xiàn)象加劇,嚴(yán)重縮短車輪服役期限。針對軌底坡的研究:任德祥等[1-2]首先分析了地鐵非對稱軌底坡對不同車輪型面下輪軌接觸幾何特性和接觸力學(xué)特性的影響,得到不同型面下軌底坡的推薦數(shù)值,然后進(jìn)一步對地鐵車輪異常磨耗現(xiàn)象進(jìn)行研究,發(fā)現(xiàn)軌底坡較大會導(dǎo)致輪軌型面匹配不合理,進(jìn)而導(dǎo)致車輛輪緣和踏面異常磨耗,最后提出了將車輪踏面外形由S1002鏇修為LM以改善車輪異常磨耗的建議;陶功權(quán)等[3-4]分析了3種類型的地鐵車輪踏面和CHN60鋼軌匹配時,軌底坡對輪軌接觸幾何、輪軌接觸力學(xué)、車輛穩(wěn)定性、曲線通過性能以及車輪磨耗的影響,分別從靜力學(xué)和動力學(xué)的角度提出地鐵車輪型面的最優(yōu)軌底坡匹配;趙越等[5]在進(jìn)行機(jī)車JM3型和貨車LM型踏面與CHN75鋼軌匹配時,分析了軌底坡對輪軌匹配狀態(tài)和輪軌滾動接觸的影響;高雅等[6]運(yùn)用輪軌接觸空間跡線法針對軌底坡對輪軌接觸幾何參數(shù)的影響展開分析,同時研究了多工況下軌底坡對車輛服役性能的影響規(guī)律;杜星等[7]分析了在標(biāo)準(zhǔn)軌底坡、對稱變化軌底坡和非對稱變化實(shí)測軌底坡條件下的車輛動力學(xué)行為,提出了不同線路下軌底坡的工程化建議;溫靜等[8]針對非對稱軌底坡對車輛動力學(xué)性能、輪軌磨耗及滾動接觸疲勞的影響進(jìn)行了研究,給出了曲線線路下軌底坡推薦數(shù)值。針對輪徑差的研究:李洪曉等[9]分析了前后轉(zhuǎn)向架都存在等值同向輪徑差對地鐵車輛曲線通過性能的影響,發(fā)現(xiàn)當(dāng)列車通過曲線線路時,外側(cè)車輪的動力學(xué)響應(yīng)更劇烈;韓鵬等[10]通過研究滾動半徑差函數(shù)形狀與位置的變化規(guī)律,分析得到型面磨耗和輪徑差對高速列車動力學(xué)性能的影響規(guī)律;李潤華等[11]研究了初始輪徑差對高速列車動力學(xué)性能的影響,并給出了初始輪徑差的限度制定標(biāo)準(zhǔn);蔣益平等[12]分析了各種輪徑差組合工況下地鐵車輛各種動力學(xué)指標(biāo)的變化規(guī)律;嚴(yán)松等[13]針對4種典型輪徑差對列車多工況運(yùn)行性能的影響進(jìn)行了研究,發(fā)現(xiàn)輪徑差越大影響越明顯;蔡送寶等[14]分析了在車橋耦合情況下,輪徑差對車輪磨耗的影響,發(fā)現(xiàn)輪徑差會導(dǎo)致車輪偏磨,也會改變車輪踏面的磨耗區(qū)域;王紅兵等[15]發(fā)現(xiàn)在4種典型輪徑差中,等值同向輪徑差導(dǎo)致的車輪踏面偏磨現(xiàn)象最明顯。

綜上,目前對軌底坡的研究主要集中在不同車輪型面的最優(yōu)軌底坡匹配及軌底坡對車輛動力學(xué)性能及車輪磨耗的影響上。對輪徑差的研究主要集中在不同種類的輪徑差對車輛動力學(xué)及車輪磨耗的影響上。實(shí)際上,鋼軌與車輪踏面接觸面有一定角度,因此通過設(shè)置軌底坡來改善輪軌接觸,隨著服役里程的變化,軌底坡和輪徑差都會發(fā)生變化,輪徑差的改變會導(dǎo)致車輪踏面與鋼軌接觸角度的改變,從而加劇輪軌接觸狀態(tài)的變化,影響車輛的動力學(xué)性能。因此,考慮不同軌底坡和輪徑差耦合工況下車輛動力學(xué)指標(biāo)變化規(guī)律,進(jìn)而研究軌底坡與輪徑差最優(yōu)匹配方案具有重要意義。筆者建立了地鐵車輛動力學(xué)模型,對9種不同軌底坡工況和5種等值同向輪徑差工況在4種曲線半徑條件下的輪軌橫向力、輪對橫移量、脫軌系數(shù)、輪重減載率和磨耗指數(shù)進(jìn)行分析,并通過熵權(quán)法對各指標(biāo)加權(quán)求和,得到不同半徑曲線下軌底坡和輪徑差耦合工況車輛動力學(xué)性能的綜合得分,獲得4種曲線半徑下軌底坡和輪徑差的最優(yōu)匹配方案。

1 地鐵車輛動力學(xué)模型

1.1 動力學(xué)模型

運(yùn)用SIMACK軟件建立如圖1所示的國內(nèi)某地鐵車輛動力學(xué)模型。該模型包括1個車體、2個構(gòu)架、4個輪對、8個軸箱和一系、二系懸掛系統(tǒng)。車輪型面選取LM型踏面,鋼軌選取UIC60軌,軌距為1 435 mm,摩擦系數(shù)為0.4。列車參數(shù)設(shè)置如表1所示。

表1 列車主要參數(shù)

圖1 車輛動力學(xué)模型Fig.1 Vehicle dynamics model

1.2 軌底坡工況設(shè)置

因?yàn)檩嗆夐g的接觸面有一定的角度,所以需要設(shè)置軌底坡來提高輪軌接觸的穩(wěn)定性,根據(jù)《地鐵設(shè)計(jì)規(guī)范》(GB 50157—2013),目前我國鐵路普遍使用1/40軌底坡,也有部分地鐵線路采用1/20軌底坡,經(jīng)過磨耗后軌底坡的數(shù)值一般為1/40～1/20。因此,在1/40～1/20之間設(shè)置了9種不同的軌底坡工況。軌底坡工況如表2所示。

表2 軌底坡工況

1.3 輪徑差設(shè)置

在SIMPACK軟件中通過Wheel geometry模塊建立輪徑差模型,輪徑差為兩側(cè)車輪名義滾動圓處直徑的差值,輪對輪徑差定義為

ΔD=D內(nèi)-D外

(1)

式中:D內(nèi)為內(nèi)側(cè)車輪的直徑;D外為外側(cè)車輪的直徑;ΔD>0表示外軌輪徑小于內(nèi)軌輪徑。

在實(shí)際運(yùn)行過程中,由于不同輪對磨耗程度不盡相同,故會產(chǎn)生各種類型的輪徑差,由于線路的影響,等值同向輪徑差比較常見,而且與其他類型相比,等值同向輪徑差對列車動力學(xué)性能和車輪磨耗的影響最為明顯[13-15],為了使每一側(cè)車輪工況保持一致,前后轉(zhuǎn)向架都設(shè)置了等值同向輪徑差,等值同向輪徑差工況如圖2所示。

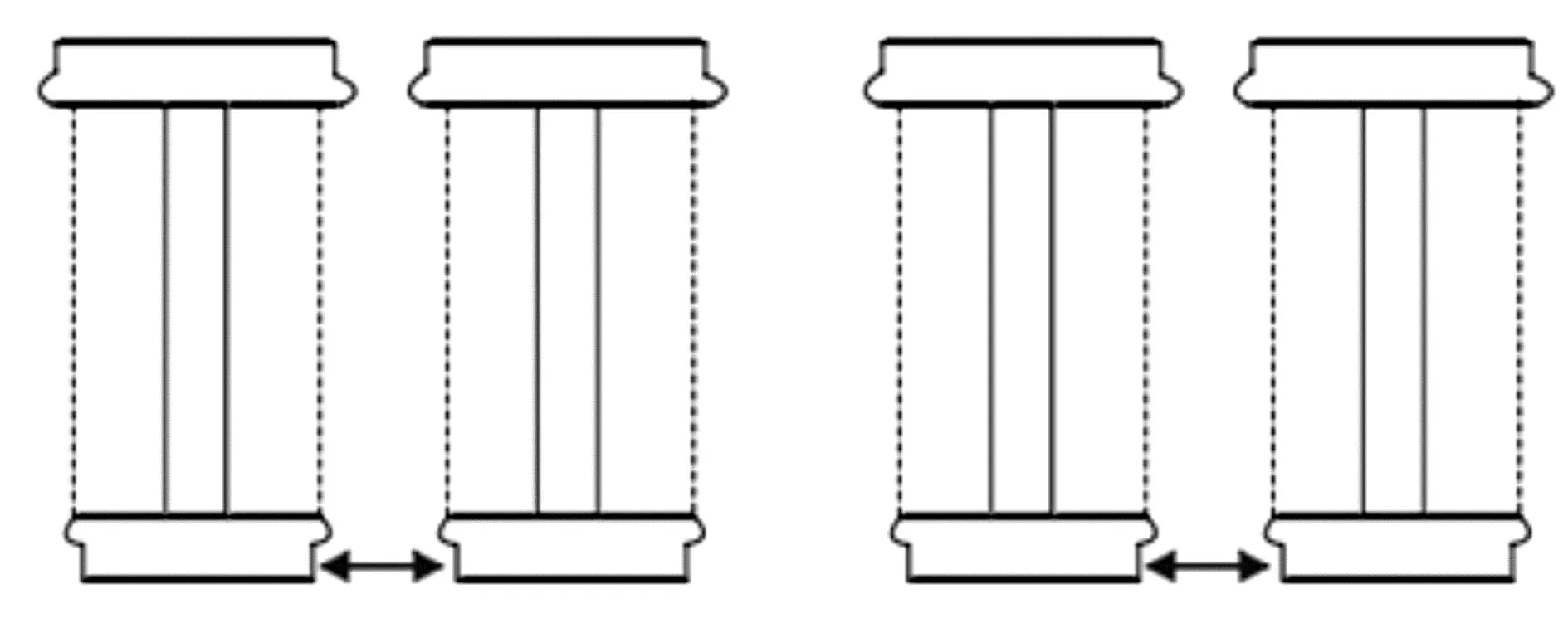
圖2 等值同向輪徑差工況Fig.2 Condition of wheel diameter difference of equal value in the same direction

根據(jù)《地鐵設(shè)計(jì)規(guī)范》(GB 50157—2013)和我國檢修規(guī)章可知,同軸輪徑差超過1 mm時就要進(jìn)行輪對鏇修。輪徑差設(shè)置如表3所示。

表3 輪徑差工況設(shè)置

1.4 線路工況設(shè)置

因?yàn)榈罔F車輛主要在城市建筑群周邊運(yùn)行,所以運(yùn)營線路中小半徑曲線較多,而且小半徑曲線線路極易導(dǎo)致車輪損傷。根據(jù)《地鐵設(shè)計(jì)規(guī)范》(GB 50157—2013),筆者選取4種不同半徑曲線作為研究對象,線路總長為1 000 m,曲線為右轉(zhuǎn)C型曲線,速度為60 km/h勻速,軌道不平順選取德國高干擾譜,線路主要參數(shù)如表4所示。

表4 線路主要參數(shù)

2 基于熵權(quán)法的綜合評價(jià)

選取輪軌橫向力、脫軌系數(shù)、輪重減載率、輪對橫移量以及外軌側(cè)車輪磨耗指數(shù)有效值和內(nèi)軌側(cè)車輪磨耗指數(shù)有效值作為地鐵車輛動力學(xué)性能的評價(jià)指標(biāo)。該6項(xiàng)指標(biāo)單位不同,量綱也不同,數(shù)據(jù)的性質(zhì)更是不盡相同,因此筆者采用熵權(quán)法,將多指標(biāo)問題按照一定規(guī)則轉(zhuǎn)換為單指標(biāo)問題,再通過線性加權(quán)的方法得到一個綜合得分,用來綜合評判地鐵車輛的動力學(xué)性能。

2.1 熵權(quán)法的原理

熵權(quán)法是一種依賴于數(shù)據(jù)本身變化規(guī)律的客觀賦權(quán)法,其指標(biāo)權(quán)重的大小根據(jù)數(shù)據(jù)本身變化特性進(jìn)行權(quán)重賦予,若某一指標(biāo)的信息熵越小,則說明該指標(biāo)的樣本變化越劇烈,提供的信息量越大,其權(quán)重系數(shù)也就越大[16]。

2.2 熵權(quán)法的步驟

選取的輪軌橫向力、脫軌系數(shù)、輪重減載率、輪對橫移量以及軌道兩側(cè)車輪磨耗指數(shù)有效值這6個評價(jià)指標(biāo)的量綱、單位不同,其數(shù)值均是越小越好。先對仿真得到的數(shù)據(jù)進(jìn)行負(fù)向指標(biāo)0～1歸一化處理,將各項(xiàng)評價(jià)指標(biāo)統(tǒng)一到[0,1]區(qū)間,其計(jì)算式為

(2)

式中:x′ij為歸一化的數(shù)據(jù);xij為第i個數(shù)據(jù)組的第j個指標(biāo);max(xj)為第j個指標(biāo)中的最大值;min(xj)為第j個指標(biāo)中的最小值。

計(jì)算第j項(xiàng)指標(biāo)下第i個樣本值占該指標(biāo)的比重,即

(3)

式中:pij為第j項(xiàng)指標(biāo)下第i個樣本值占該指標(biāo)的比重。

計(jì)算第j項(xiàng)指標(biāo)的熵值和信息熵冗余度,即

(4)

dj=1-ej

(5)

式中:ej為第j項(xiàng)指標(biāo)的熵值,且k=1/lnn>0,并滿足ej≥0;dj為熵值冗余度。

計(jì)算各樣本的權(quán)重,得到不同半徑曲線下這6個指標(biāo)的權(quán)重系數(shù)wj,即

(6)

通過對不同工況下的6個指標(biāo)進(jìn)行加權(quán)求和得到不同工況下各樣本的綜合得分si,即

(7)

3 計(jì)算結(jié)果分析

建立地鐵車輛動力學(xué)仿真模型,設(shè)置了45種軌底坡和輪徑差耦合工況,分析在4種不同C型曲線半徑條件下,輪軌橫向力、脫軌系數(shù)、輪重減載率、輪對橫移量和輪軌磨耗指數(shù)的變化規(guī)律。

3.1 輪軌橫向力

輪軌橫向力是地鐵列車曲線通過性能的重要評價(jià)指標(biāo),輪軌橫向力Q計(jì)算式為

Q≤0.4(Pst1+Pst2)

(8)

式中:Pst1,Pst2分別為左輪及右輪靜載荷,kN。

不同曲線半徑下輪軌橫向力峰值如圖3所示。由圖3可知:1) 在4種曲線半徑條件下,當(dāng)軌底坡恒定時,隨著輪徑差從-1 mm變化至1 mm,輪軌橫向力峰值均逐漸變大;2) 在曲線半徑為300,400 m條件下,當(dāng)輪徑差恒定時,軌底坡對輪軌橫向力峰值的影響并不是很明顯,在曲線半徑為500,600 m條件下,當(dāng)輪徑差恒定,內(nèi)軌軌底坡不變時,隨著外軌軌底坡的增大,輪軌橫向力峰值逐漸變大,與內(nèi)軌軌底坡相比,外軌軌底坡的變化對輪軌橫向力峰值的影響更大;3) 隨著曲線半徑的增大,軌底坡和輪徑差對輪軌橫向力峰值的影響程度在逐漸變大。

圖3 不同曲線半徑下輪軌橫向力峰值Fig.3 Peak wheel-rail lateral force under different curve radii

3.2 輪對橫移量

輪對橫移量是評價(jià)列車曲線通過性能的重要指標(biāo),輪對橫移量較大時會發(fā)生輪緣接觸,從而導(dǎo)致踏面異常磨耗,惡化輪軌接觸關(guān)系。不同曲線半徑下列車輪對橫移量峰值如圖4所示。由圖4可知:1) 在4種曲線半徑條件下,當(dāng)軌底坡恒定時,隨著輪徑差從-1 mm變化至1 mm,輪對橫移量峰值均逐漸變大;2) 在4種曲線半徑條件下,當(dāng)輪徑差恒定,內(nèi)軌軌底坡不變時,隨著外軌軌底坡的增大,輪對橫移量峰值逐漸變大;3) 隨著曲線半徑的增大,軌底坡和輪徑差對輪對橫移量峰值的影響程度逐漸變大,當(dāng)軌底坡和輪徑差恒定時,隨著曲線半徑的增大,輪對橫移量逐漸減小。

圖4 不同曲線半徑下列車輪對橫移量峰值Fig.4 Peak values of wheelset traverse under different curve radii

3.3 脫軌系數(shù)

車輛運(yùn)行過程中,運(yùn)行環(huán)境和線路條件等不利因素均可導(dǎo)致列車發(fā)生輪軌分離現(xiàn)象,繼而威脅車輛運(yùn)行質(zhì)量以及乘客生命安全。根據(jù)《機(jī)車車輛動力學(xué)性能評定及試驗(yàn)鑒定規(guī)范》(GB 5599—2019),脫軌系數(shù)安全值為0.8,即

(9)

式中:P為輪軌垂向力,kN;Q為輪軌橫向力,kN。

不同曲線半徑下脫軌系數(shù)峰值如圖5所示。由圖5可知:1) 在4種曲線半徑條件下,當(dāng)軌底坡恒定時,隨著輪徑差從-1 mm變化至1 mm,脫軌系數(shù)峰值均逐漸變大;2) 在曲線半徑為300 m條件下,當(dāng)輪徑差恒定時,軌底坡對脫軌系數(shù)峰值的影響并不是很明顯,在曲線半徑為400,500,600 m條件下,當(dāng)輪徑差恒定,內(nèi)軌軌底坡不變時,隨著外軌軌底坡的增大,脫軌系數(shù)峰值逐漸變大,當(dāng)曲線半徑大于300 m時,與內(nèi)軌軌底坡相比,外軌軌底坡的變化對輪軌橫向力峰值的影響更大;3) 隨著曲線半徑的增大,軌底坡和輪徑差對脫軌系數(shù)峰值的影響程度在逐漸變大。

圖5 不同曲線半徑下脫軌系數(shù)峰值Fig.5 Peak value of derailment coefficient under different curve radii

3.4 輪重減載率

不同曲線半徑下輪重減載率峰值如圖6所示。由圖6可知:當(dāng)軌底坡和輪徑差恒定時,隨著曲線半徑的增大,輪重減載率逐漸變小。相同曲線半徑下,輪徑差和軌底坡對輪重減載率的影響不是很明顯,且變化幅度在0.02以內(nèi)。當(dāng)列車速度小于160 km/h時,輪重減載率要控制在0.65以內(nèi)。所有工況下輪重減載率均在限制范圍之內(nèi)。

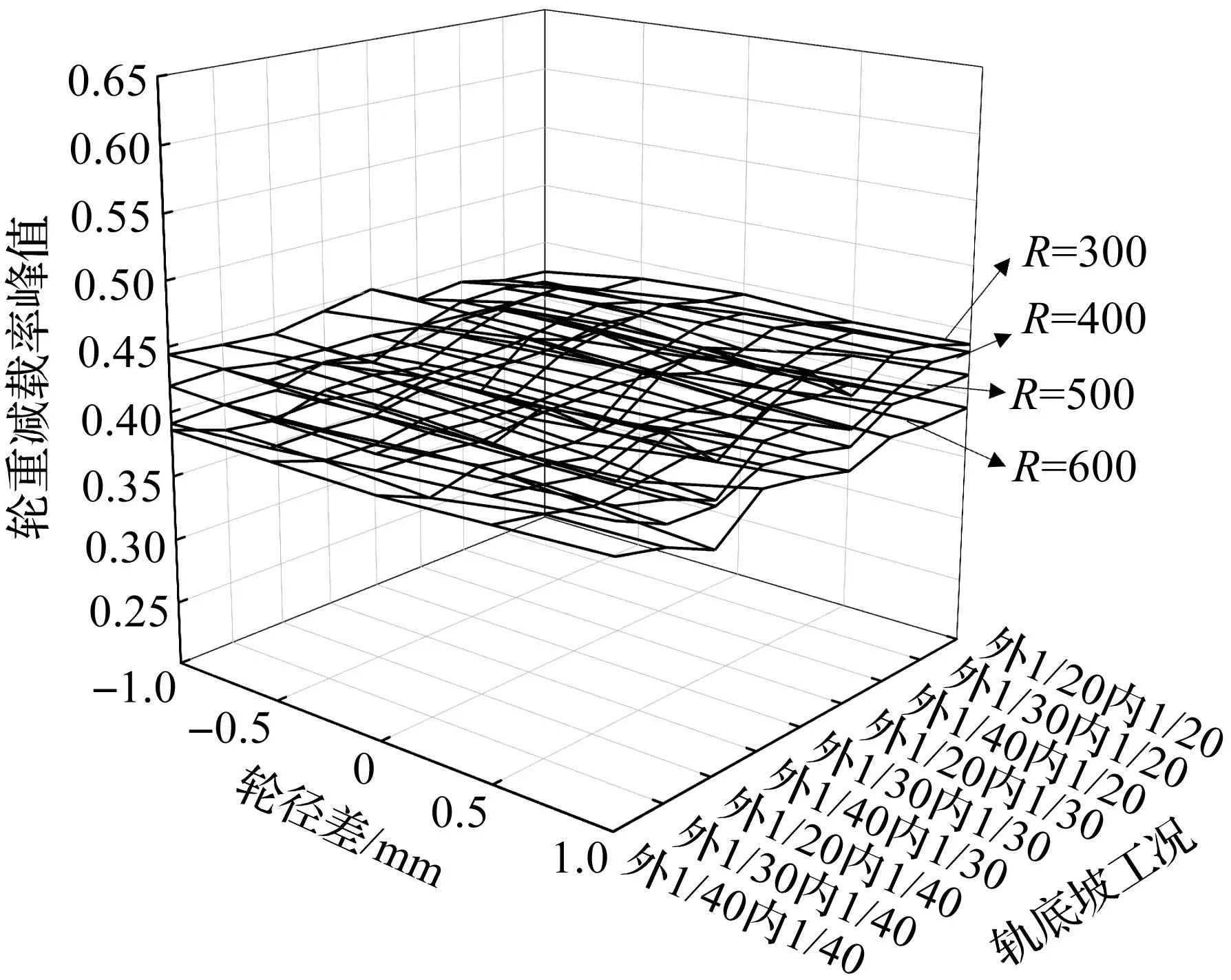
圖6 不同曲線半徑下輪重減載率峰值Fig.6 The peak value of wheel load shedding rate under different curve radii

3.5 磨耗指數(shù)

相較于其他磨耗指數(shù),Elkins磨耗指數(shù)更能有效地表示輪軌之間的磨損現(xiàn)象,更適合研究輪軌間的磨耗問題,磨耗指數(shù)W的計(jì)算式為

W=Txξx+Tyξy

(10)

式中:Tx為橫向蠕滑力;ξx為橫向蠕滑率;Ty為縱向蠕滑力;ξy為縱向蠕滑率。為了更加準(zhǔn)確地反映輪軌的磨耗程度,選取磨耗指數(shù)的有效值RMS作為評價(jià)指標(biāo)。

不同曲線半徑下車輪磨耗指數(shù)有效值如圖7所示。由圖7可知:1) 在相同輪徑差、軌底坡和曲線半徑工況下,外軌車輪磨耗指數(shù)有效值要大于內(nèi)軌車輪磨耗指數(shù)有效值,而且內(nèi)外軌車輪的磨耗指數(shù)有效值變化規(guī)律基本一致;2) 在4種曲線半徑條件下,當(dāng)軌底坡恒定時,隨著輪徑差從-1 mm變化至1 mm,磨耗指數(shù)有效值在逐漸變小,這說明外軌輪徑大于內(nèi)軌輪徑工況會加重兩側(cè)車輪的磨耗;3) 在4種曲線半徑條件下,當(dāng)輪徑差恒定,內(nèi)軌軌底坡不變時,隨著外軌軌底坡的增大,磨耗指數(shù)有效值逐漸變小;4) 隨著曲線半徑的增大,軌底坡和輪徑差對磨耗指數(shù)有效值的影響程度在逐漸變小;5) 隨著曲線半徑的增大,內(nèi)外軌車輪磨耗指數(shù)有效值逐漸減小,且內(nèi)外軌車輪磨耗指數(shù)有效值差距逐漸變小,這說明列車通過曲線的半徑越小,車輪偏磨越嚴(yán)重;6) 當(dāng)外軌軌底坡為1/40,內(nèi)軌軌底坡為1/20,輪徑差為-1 mm時,車輪兩側(cè)磨耗指數(shù)有效值最大,在這個工況下通過半徑為300 m曲線,外軌車輪的磨耗指數(shù)有效值接近100 N,車輪磨耗已經(jīng)十分嚴(yán)重,應(yīng)盡可能避免出現(xiàn)這種工況。

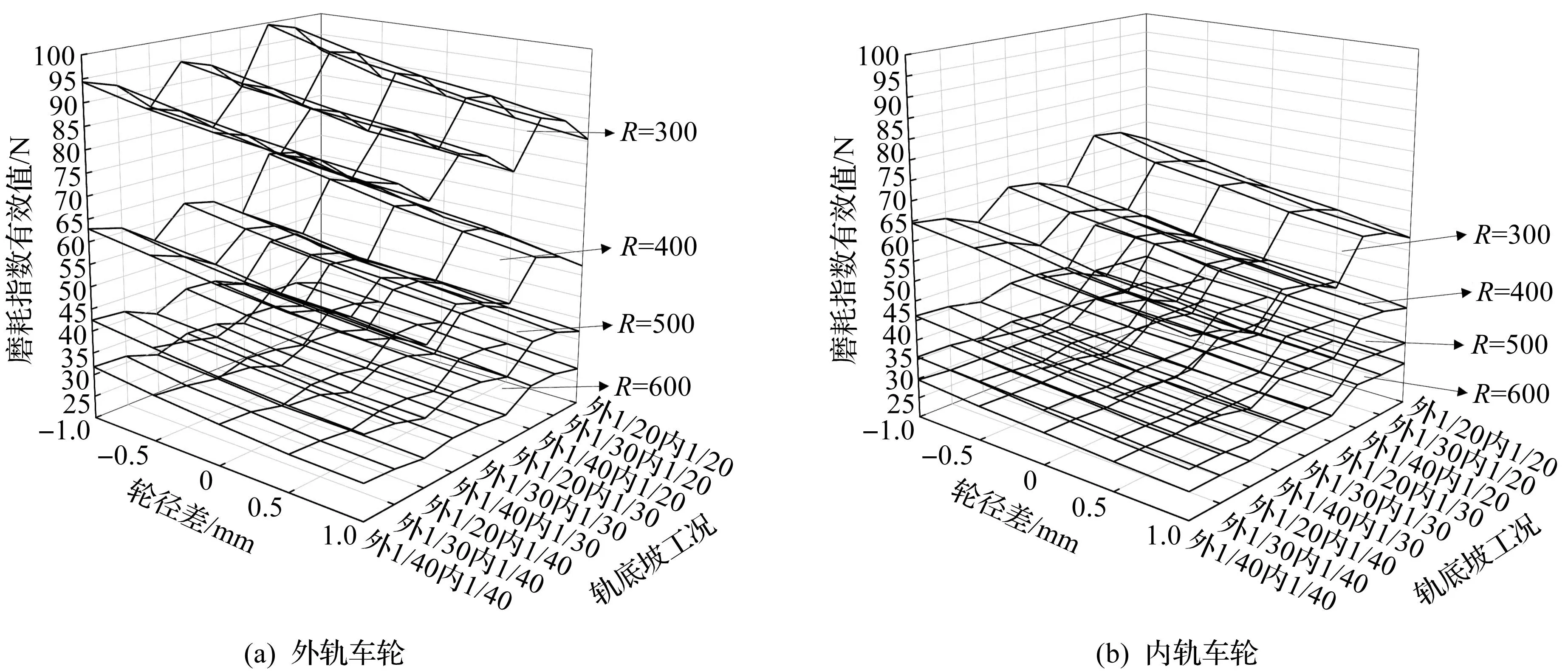
圖7 不同曲線半徑下車輪磨耗指數(shù)有效值Fig.7 Effective value of wheel wear index under different curve radii

4 基于熵權(quán)法的車輛動力學(xué)性能綜合評價(jià)

根據(jù)輪軌橫向力、脫軌系數(shù)、輪重減載率、輪對橫移量以及內(nèi)外軌車輪磨耗指數(shù)有效值的計(jì)算結(jié)果,首先進(jìn)行數(shù)據(jù)的標(biāo)準(zhǔn)化;然后采用熵權(quán)法進(jìn)行數(shù)據(jù)分析;最后計(jì)算出各項(xiàng)指標(biāo)在不同曲線半徑下的信息熵值和信息熵冗余度,從而求得各項(xiàng)指標(biāo)的權(quán)重,結(jié)果如表5所示。

表5 不同曲線半徑下各項(xiàng)指標(biāo)權(quán)重系數(shù)

由表5可知:在同一個半徑曲線下,各項(xiàng)評價(jià)指標(biāo)的權(quán)重系數(shù)相差十分明顯,且曲線半徑不同,各項(xiàng)指標(biāo)規(guī)律也不同。在曲線半徑為300,400 m時,內(nèi)外軌車輪磨耗指數(shù)的權(quán)重系數(shù)更大;在曲線半徑為500,600 m時,輪軌橫向力和脫軌系數(shù)所占的權(quán)重系數(shù)更大。

根據(jù)表5的計(jì)算結(jié)果以及式(7)得到在4種曲線半徑條件下不同耦合工況的綜合得分。綜合得分越低,綜合動力學(xué)性能越好,對應(yīng)的列車運(yùn)行工況越理想,綜合得分結(jié)果如圖8所示。由圖8可知:當(dāng)輪徑差和軌底坡工況不變時,隨著曲線半徑的增大,綜合得分逐漸變小,即車輛動力學(xué)性能得到改善。當(dāng)軌底坡工況一定時,輪徑差由-1 mm變化至1 mm,曲線半徑為300,400 m時對應(yīng)的綜合得分逐漸變小;而曲線半徑為500,600 m時對應(yīng)的綜合得分逐漸變大。當(dāng)輪徑差工況一定且內(nèi)軌軌底坡不變時,隨著外軌軌底坡逐漸變大,曲線半徑為300,400 m對應(yīng)的綜合得分逐漸變小;而曲線半徑500,600 m對應(yīng)的綜合得分逐漸變大。

圖8 不同曲線半徑下綜合得分Fig.8 Comprehensive scores under different curve radii

在同一曲線半徑下的45種工況中找出綜合得分最低(即車輛動力學(xué)性能最佳)的前3種工況,結(jié)果如表6所示。由表6可知,以車輛動力學(xué)綜合性能最優(yōu)為目標(biāo),軌底坡和輪徑差最佳匹配規(guī)律如下:1) 隨著曲線半徑的增大,呈現(xiàn)出外軌軌底坡逐漸變小、內(nèi)軌軌底坡逐漸變大的趨勢,當(dāng)曲線半徑為300,400 m時,外軌軌底坡大于內(nèi)軌軌底坡,當(dāng)曲線半徑為500,600 m時,內(nèi)軌軌底坡大于外軌軌底坡;2) 隨著曲線半徑的增大,輪徑差數(shù)值有變小趨勢,從+1 mm變至-1 mm,當(dāng)曲線半徑為300,400 m時,外軌輪徑小于內(nèi)軌輪徑,當(dāng)曲線半徑為500,600 m時,外軌輪徑大于內(nèi)軌輪徑;3) 在曲線半徑為300,400,500,600 m 4種工況下,外軌軌底坡,內(nèi)軌軌底坡,輪徑差最優(yōu)匹配方案分別為(1/20,1/40,+1),(1/20,1/40,+1),(1/30,1/30,-1),(1/40,1/30,-1)。

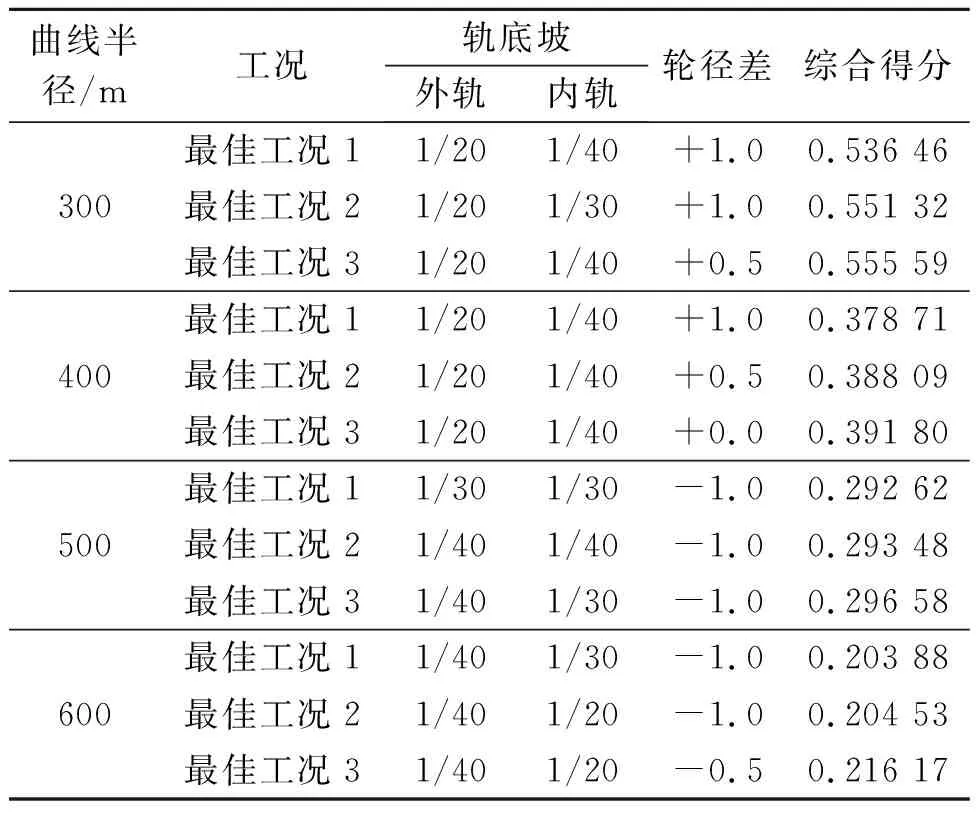
表6 不同曲線半徑下綜合得分排名

5 結(jié) 論

筆者建立了地鐵車輛動力學(xué)模型,設(shè)置了9種軌底坡和5種輪徑差工況,分析了在4種曲線半徑條件下輪軌橫向力、輪對橫移量、脫軌系數(shù)、輪重減載率和輪軌磨耗指數(shù)的變化規(guī)律,通過熵權(quán)法對上述指標(biāo)進(jìn)行加權(quán)求和,得到不同曲線半徑、不同耦合工況下地鐵車輛動力學(xué)性能綜合得分,從而得出不同曲線半徑下軌底坡與輪徑差的最佳匹配,具體結(jié)論如下:1) 隨著曲線半徑的增大,輪徑差和軌底坡變化對輪軌橫向力、輪對橫移量和脫軌系數(shù)的影響程度越來越大,而對輪軌磨耗指數(shù)的影響越來越小。當(dāng)軌底坡一定時,輪徑差從-1 mm變化至1 mm,脫軌系數(shù)、輪軌橫向力和輪對橫移量均逐漸變大,而輪軌磨耗指數(shù)逐漸變小;當(dāng)輪徑差恒定且內(nèi)軌軌底坡不變時,隨著外軌軌底坡的增大,輪軌橫向力、輪對橫移量和脫軌系數(shù)逐漸變大而輪軌磨耗指數(shù)逐漸變小;輪徑差和軌底坡耦合工況對輪重減載率影響不明顯。2) 當(dāng)軌底坡和輪徑差工況不變時,隨著曲線半徑的增大,綜合得分逐漸降低,即車輛動力學(xué)綜合性能逐漸改善。當(dāng)軌底坡工況一定時,輪徑差從-1 mm變化至1 mm,曲線半徑300,400 m對應(yīng)的車輛動力學(xué)綜合性能逐漸增加;而曲線半徑500,600 m對應(yīng)的車輛動力學(xué)綜合性能逐漸減小。當(dāng)輪徑差工況一定時,內(nèi)軌軌底坡不變,外軌軌底坡逐漸變大,曲線半徑300,400 m對應(yīng)的車輛動力學(xué)綜合性能逐漸增加,而曲線半徑500,600 m對應(yīng)的車輛動力學(xué)綜合性能逐漸減小。3) 在半徑曲線為300,400 m條件下,當(dāng)外軌輪徑小于內(nèi)軌輪徑且外軌軌底坡大于內(nèi)軌軌底坡時,車輛動力學(xué)綜合性能最優(yōu);而在曲線半徑為500,600 m條件下,當(dāng)外軌輪徑大于內(nèi)軌輪徑且外軌軌底坡小于內(nèi)軌軌底坡時,車輛動力學(xué)綜合性能最優(yōu)。以車輛動力學(xué)性能綜合評價(jià)為依據(jù),在曲線半徑為300,400,500,600 m 4種工況下,外軌軌底坡、內(nèi)軌軌底坡和輪徑差最優(yōu)匹配方案分別為(1/20,1/40,+1),(1/20,1/40,+1),(1/30,1/30,-1),(1/40,1/30,-1)。研究結(jié)果可為不同曲線半徑線路下軌底坡和輪徑差的設(shè)置提供一定的技術(shù)支持,在實(shí)際應(yīng)用過程中,可以根據(jù)線路的軌底坡狀態(tài)對車輪鏇修進(jìn)行指導(dǎo)。

本文得到了北京建筑大學(xué)研究生創(chuàng)新項(xiàng)目(PG2022133)的支持。