基于稀疏恢復的雷達信號處理研究綜述

全英匯 吳耀君 段麗寧 徐 剛 薛 敏 劉智星 邢孟道

①(西安電子科技大學電子工程學院 西安 710071)

②(西安市先進遙感重點實驗室 西安 710071)

③(東南大學信息科學與工程學院毫米波全國重點實驗室 南京 210096)

④(西安電子科技大學前沿交叉研究院 西安 710071)

1 引言

當信號通過某些特征空間進行表示時，只有很少部分系數非零，且非零元素的個數遠遠小于信號的長度，此時可以認為信號在該特征空間中是稀疏的，將稀疏性的先驗信息引入到信號處理過程可有效解決傳統信號處理技術無法解決的技術難題。基于稀疏性的信號處理中，先驗稀疏性以信號處理的約束條件形式存在，基于稀疏性約束進行信號處理的歷史由來已久[1]，在20世紀稀疏信號處理技術就已被應用于圖像處理等領域，但是整體而言稀疏信號處理處于較為緩慢的發展階段。2006年，著名的壓縮感知模型被提出[2]，Candès從數學角度對該理論的一些關鍵問題開展了研究，極大推動了壓縮感知理論的發展與完善。壓縮感知理論突破了傳統的采樣定理，可從遠小于傳統理論所需的采樣值中恢復出原始信號。該理論的基本條件是信號稀疏，通常采用范數對稀疏信號的稀疏度進行度量，?0范數優化為恢復稀疏信號提供了有力工具，但是該問題難以求解。Donoho等人[3]研究了最小?0范數解的唯一性問題，證明了最小?1范數解與最小?0范數解的等效性，推動了?1范數重構算法的發展。之后出現了如迭代閾值類算法、梯度投影重構算法以及最小絕對收縮和選擇算法(Least Absolute Shrinkage and Selection Operator,LASSO)等的求解方法。Mallat等人[4]首次將匹配追蹤算法應用到了信號稀疏分解任務，之后大量學者開展了如正交匹配追蹤等算法的研究；稀疏貝葉斯學習算法也被應用于求稀疏解。2010年，Gregor等人[5]設計了算法深度展開框架，從該工作中衍生出的模型驅動自學習思想為高效稀疏恢復算法提供了新的思路[6]。針對網格失配問題，也涌現出了基于動態詞典[7]與無網格壓縮感知模型的稀疏恢復方法[8]。

伴隨著壓縮感知的模型[9-11]、求解算法[12-14]與性能邊界分析[15-17]等相關理論的逐步完善，基于壓縮感知的稀疏信號處理技術在雷達探測[18]、陣列信號處理[19,20]、圖像處理、遙感成像[21-23]、無線通信[24-26]等領域廣泛應用，由于現代雷達探測場景的目標稀疏特性，稀疏信號處理在雷達中的應用更是獲得了廣泛而迅猛的發展[27-29]。2007年，Baraniuk等人[18]首次正式討論了壓縮感知原理在雷達成像中的應用，證明了壓縮感知應用于雷達成像的可行性。2009年，Herman等人[30,31]對基于壓縮感知的距離-多普勒雷達的目標高分辨展開研究。Mishali等人[32]在2010年較為系統地提出了一種基于壓縮感知理論的寬帶稀疏信號采集系統。Ender等人[33]較為系統地探討了壓縮感知理論在雷達系統中的脈沖壓縮、雷達成像、波達方向估計等方面的應用。Yu等人[34]對壓縮感知理論在多輸入多輸出雷達系統的應用展開了研究。

稀疏信號處理技術在雷達信號處理中的作用可分為兩個方面。一方面，稀疏信號處理被用于解決傳統體制雷達信號處理中的固有問題，以提升雷達目標探測性能、抗干擾性能以及雷達成像性能等[31,35-39]。另一方面，隨著雷達目標特性測量、抗干擾等需求的不斷發展，雷達的探測任務日益復雜化，硬件性能約束下的多任務雷達體制也日新月異，催生了比如頻域稀疏雷達、稀疏陣列雷達等新型雷達體制，與傳統體制雷達相比，此類雷達往往具備低成本、輕量化、體積小、抗干擾性能強等系統級優勢，但是此類新體制雷達卻使得傳統信號處理方法不再適用，為此相關學者將壓縮感知模型引入新體制雷達的信號處理中，來完成此雷達的波束形成[40-42]、目標參數估計[43-45]與成像[46-48]等?，F代雷達的典型數字信號處理流程為空域處理、脈沖壓縮、相參處理以及目標檢測。稀疏信號處理作為一種通用信號處理方法，被廣泛應用于不同體制雷達的各個信號處理環節。

2 壓縮感知理論模型

隨著數字信號處理技術的快速發展，如何從龐大的數據中穩定有效地提取出有用信息，剔除冗余信息，感知和挖掘信息內在結構和規律，是人們關注的重點問題。傳統的奈奎斯特采樣定理要求信號的采樣頻率必須大于信號帶寬的兩倍，才能完整地恢復原始信號，隨著信號帶寬的增大以及探測精度的提升，奈奎斯特采樣框架對硬件采樣帶來了巨大壓力，制約著信號的處理過程。為此，壓縮感知[2,9-11,49-52]采樣框架應運而生。壓縮感知采樣可以同時完成信號的壓縮和采樣、減小采樣率、降低信號存儲和傳輸壓力，從而降低硬件成本，具有重要的理論意義和應用價值。

2.1 壓縮感知模型

使用壓縮感知方法的前提條件是信號是否具有稀疏性，若信號在某些基映射下可表示為稀疏形式，則稱信號是稀疏的。

假設一個長度為N的離散信號x=[x(1),x(2),...,x(N)]∈CN可由一組變換基矩陣Ψ=[ψ1,ψ2,...,ψN]的線性組合表示為[2]

其中，Ψ為變換基；θ為基矩陣對應的N×1維的向量，包含K(K?N)個非零元素，由投影系數θi組成，是離散信號x在變換基下的另一種表示方式。此時θ中的非零元素很少，且滿足：

則可認為信號x在Ψ域下是K-稀疏的。其中‖·‖0為向量的?0范數，‖θ‖0表示θ中非零元素的個數。但實際的信號中往往混雜著噪聲，使得很難嚴格滿足以上述稀疏性的條件，此時θ包含少量較大數值的系數，其余的系數較小，稱這類信號為近似稀疏信號。

信號的稀疏性可以理解為信號在某個變換域下的分布特性，對同一信號，在不同的變換域中表示各有不同，不存在一個唯一的最佳稀疏變換基，選擇何種變換基要根據實際信號特征來決定，由于變換基選取通常會決定稀疏恢復的效果，因此在基于壓縮感知模型的雷達信號處理中，如何選擇稀疏特征域對雷達回波進行稀疏表征，是建立雷達信號處理的壓縮感知模型進而實現目標參數穩健估計的關鍵。

壓縮觀測作為壓縮感知過程的另一關鍵環節，其與傳統采樣框架最大的不同是不對接收信號直接采樣，而是先對信號做壓縮處理。壓縮觀測通過觀測矩陣將高維稀疏信號投影到低維空間上，保留信號的有效特征量。這樣在采樣過程中可以降低采樣壓力，僅對信號的有效信息進行采樣。

壓縮觀測過程最重要步驟是構造觀測矩陣，適合的觀測矩陣可顯著提升壓縮感知理論的應用效果。本文用Φ∈CM×N來代表觀測矩陣，通過其對長度為N的信號x進行壓縮采樣后，可以得到長度為M(M ?N)的觀測向量y，壓縮觀測過程可表示為

將式(1)代入式(3)可以得到：

其中，Θ=ΦΨ為M×N的矩陣，稱為感知矩陣。式(4)未知量個數遠遠大于方程的個數，屬于欠定問題，有無窮多組解。壓縮感知理論通過給上述問題增加?0范數約束，將通過少量線性觀測恢復出原始稀疏信號的問題轉化為

整個壓縮觀測過程如圖1所示。

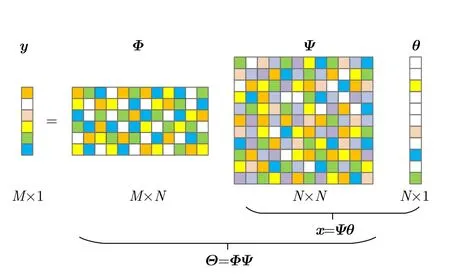
圖1 壓縮觀測過程Fig.1 The process of compressing observations

壓縮感知采樣框架下的信號恢復是一個非線性約束問題，考慮到實際觀測信號中會不可避免混雜噪聲，在噪聲條件下，信號重構可用?0范數優化問題表示為

其中，ε的值由噪聲能量決定。

若要精確的恢復信號，Θ需要滿足一定的列正交性或者近似正交性[3,53-55]。針對矩陣相關性，有兩種常用的衡量方式，一種是約束等距性條件(Restricted Isometry Property,RIP)，一種是互不相干性(Mutual Incoherence Property,MIP)，矩陣的MIP條件或者RIP條件為稀疏恢復算法提供了理論保證。Candès和Tao在文獻[56]中提出使用RIP性質對矩陣的正交性進行度量，用數學表達式可寫為

其中，δK是約束等容常數，值比較小，一般δK＜1 ；θ為K-稀疏向量；當Θ使得式(7)對于任意滿足?0范數小于等于K的θ成立時，我們就稱Θ滿足稀疏度為K的RIP條件，則可以保證稀疏向量的穩健重構。

對于一個確定性的矩陣，矩陣的MIP特性通過最大相干系數進行衡量，Θ=[α0,α1,...,αn,...,αN-1]，則最大相干系數定義為

其中，〈ai,aj〉為ai,aj內 積的模 值，‖ai‖2為ai的?2范 數。當最大相干系數滿足μ(Θ)＜1/(2K-1)時[57]，可對K-稀疏向量θ精確求解，該矩陣Θ具有MIP特性。壓縮感知中，有多種對矩陣性質的度量指標，除了RIP,MIP性質之外，還有零空間性質(Null Space Property,NSP)，L1-約束最小奇異值[53](L1-Constrained Minimal Singular Value,L1-CMSV)等多種性質。

傳統的壓縮感知理論中，稀疏信號的非零元素是隨機分布的，但是在許多稀疏信號中，非零元素存在一定的結構，由此發展出如圖稀疏結構[58]、塊稀疏結構[59]、動態字典模型[7]、無網格模型[8]以及樹狀稀疏[60]等新模型。當信號中非零的元素成塊出現時，稱其為塊稀疏信號，塊稀疏的結構特性與雷達目標的特性具有很強的一致性，可以在雷達目標參數估計等應用中獲得相較于傳統算法更好的性能[61]。

2.2 優化重構

式(6)的求解是NP難(Non-Deterministic Polynomial-Time Hard)問題，實際中難以直接求解，目前對壓縮感知模型的求解算法主要有凸松弛算法、貪婪追蹤算法以及稀疏貝葉斯算法等。

(1) 凸松弛算法：此算法的本質是求解一個凸優化問題的最小值來重構稀疏信號。將?0范數最小化的NP難問題轉化為對?1范數最小化的求解，將對非凸問題的求解轉換為對凸優化問題的求解，來尋找全局最優解。典型算法包括：基追蹤(Basis Pursuit,BP)[62]、迭代閾值(Iterative Thresholding)[63]等算法。該類算法估計能力較強，重構精度高，但是運算實時性較差，很難滿足實際工程的需求。

(2) 貪婪追蹤算法：該算法包括典型的如匹配追蹤(Matching Pursuit,MP)[12]、正交匹配追蹤(Orthogonal Matching Pursuit,OMP)[13]、正則化匹配追蹤(Regularized OMP,ROMP)[14,64]和壓縮采樣匹配追蹤(Compressive Sampling Matching Pursuit,CoSaMP)[65]等算法，其基于?0范數最小化策略，在每一次的循環迭代中利用最小二乘法對當前的殘差向量進行更新，選擇局部最優解，以此實現稀疏信號的重構。該類算法計算量較小，運算速度較快，但信號恢復精度較差。

(3) 稀疏貝葉斯算法(Sparse Bayesian Learning,SBL)[66,67]：該類算法將稀疏信號的重構問題轉化為稀疏信號各元素的似然估計問題。首先根據信號的先驗分布，采用貝葉斯理論進行概率計算，得到目標參數的后驗分布，并對其進行參數估計。將稀疏貝葉斯算法應用到探地雷達成像領域中可降低數據存儲量及數據采集成本，且在低信噪比(Signal to Noise Ratio,SNR)下成像效果更好[68]。

塊稀疏是稀疏信號的特殊情形，經典的壓縮感知重構算法可以對其進行處理，但是采用塊CS重構算法，利用塊稀疏信號的非零元素成塊特點，可以獲得相較于傳統算法更好的性能[69]。典型的塊稀疏恢復算法分為兩類，分別是凸優化類算法以及貪婪追蹤類算法。凸優化類算法如混合?2/?1范數優化算法，貪婪追蹤類算法如由MP和OMP擴展來的塊匹配追蹤算法以及塊正交匹配追蹤算法[70]。

3 雷達回波信號的稀疏特性

當滿足稀疏性的先驗要求時[15]，稀疏恢復技術可應用于傳統體制雷達的信號處理；同時稀疏恢復技術也可應用于新體制雷達，用于解決傳統信號處理方法不適用新雷達體制的問題。因此本節主要討論傳統體制雷達中的場景稀疏性與新體制雷達中的稀疏觀測，為第4節的基于稀疏恢復的信號處理奠定基礎。

3.1 場景稀疏

場景的稀疏性指的是雷達觀測場景中的目標稀疏性，由目標的個數、尺寸、形狀、材質等物理特性所決定，體現為雷達信號處理特征域下的稀疏。如在點目標探測中，目標的距離與速度只占據了有限個距離單元與多普勒單元；在雷達的高分辨一維距離像中，典型飛機目標的一維距離像只有有限個強散射點；在合成孔徑雷達(Synthetic Aperture Radar,SAR)或者逆合成孔徑雷達(Inverse Synthetic Aperture Radar,ISAR)成像中，目標呈現散射點分布，散射點個數遠小于成像單元個數。下面結合窄帶與寬帶兩種雷達體制依次討論場景的稀疏性。

(1) 窄帶雷達場景

目標個數的稀疏性是場景稀疏性的主要決定因素，在雷達觀測場景中，受雷達威力以及波束寬度的限制，通常探測的目標數量小于雷達分辨單元個數，目標個數是稀疏的。但同時目標個數的稀疏性會和目標的特征域特征相結合，最終體現為信號處理特征域上的稀疏性，本文從時域、頻域、空間域以及聯合特征域對場景稀疏性進行分析。

(a) 時域稀疏

在時域稀疏性方面，回波信號經過脈沖壓縮處理后，目標在粗分辨距離單元上呈現有限個強幅值響應點，強幅值點數遠遠小于整個快時間采樣點數，具備時域上的稀疏性。

(b) 頻域稀疏

在頻域稀疏性方面，在雷達探測場景中，探測的目標個數稀疏時，對應分布在多普勒頻率單元的強幅值點是稀疏的，頻域具備稀疏性。

(c) 空間域稀疏

雷達探測場景中，目標僅占據少量的角度分辨單元，即目標在空域內是稀疏的。

(d) 距離-多普勒域

雷達探測場景中目標個數稀疏時，位于相同或不同距離單元的目標具備不同的多普勒，相應地，目標分布在距離-多普勒特征域的強幅值點是有限的，且強幅值點個數遠小于距離-多普勒單元個數，目標在距離-多普勒單元上呈現稀疏分布[71]。

(2) 寬帶雷達場景

根據雷達的分辨理論，雷達的距離分辨率與其帶寬成反比，當雷達帶寬足夠大時，雷達距離分辨單元小于目標尺寸，目標不再由點目標模型表征，而是由更為復雜的散射特性進行描述。在SAR和ISAR等寬帶高分辨雷達應用中，大帶寬目標回波經過脈沖壓縮處理，目標上各散射中心的回波將分布在不同的距離單元中，而目標的回波通常由幾個強散射中心構成，強散射中心在成像平面上僅占很少的像素單元，具備稀疏性。

3.2 稀疏觀測

雷達稀疏觀測由雷達的體制、觀測方式等決定，多體現為雷達系統設計或者雷達發射波形在各個特征域下的稀疏性，同時也會帶來對探測場景的信息稀疏。比如稀疏陣列雷達的陣元分布為均勻布陣雷達的非完整采樣，對目標在空域進行稀疏觀測，具備空域稀疏性；頻率捷變雷達發射的頻率為工作帶寬內的頻率子集，對目標在頻域稀疏觀測，具備頻域稀疏性。下面對典型的頻域稀疏雷達與空域稀疏雷達進行討論。

(1) 頻域稀疏雷達

頻域稀疏雷達是指雷達發射的波形中，頻點具備稀疏性。雷達通過稀疏頻率發射的方式提升電子對抗裝備對雷達頻點的分選識別難度。因而頻率稀疏波形在雷達中得到了廣泛應用，典型的頻域稀疏雷達體制有頻率捷變雷達、頻率稀疏編碼雷達以及稀疏捷變-正交頻分復用(Sparse Frequency Agile Orthogonal Frequency Division Multiplexing,SFA-OFDM)雷達。

頻率捷變雷達為雷達在相鄰脈沖間進行載頻隨機/偽隨機跳變的雷達體制。頻率捷變雷達誕生于第二次世界大戰期間，受限于當時電子器件的發展水平與信號處理水平，頻率捷變雷達在誕生初期只能工作在非相參模式下[72]，但隨著電子技術的不斷發展，頻率捷變雷達逐步實現了全相參的工作能力。全相參頻率捷變雷達的典型波形如圖2所示[73]，其中，f0為初始載波頻率，Δf為跳頻間隔，Tr為脈沖重復周期；雷達在相鄰的脈沖間進行頻率跳變，同時每個相參處理間隔內，雷達的有效頻點為其工作總帶寬的一個子集，即一個相參處理間隔內的信號載頻具有頻率稀疏性。

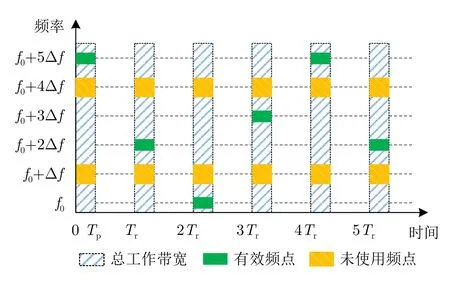
圖2 頻率捷變波形示意圖Fig.2 Schematic diagram of frequency agile signal

頻率稀疏編碼雷達是指對單個脈沖內的信號劃分子脈沖，對其進行稀疏頻率編碼。與脈間頻率捷變雷達相似，頻率編碼波形也按照一定的隨機/偽隨機方式對頻率序列進行設計，其典型的頻率編碼波形可以是頻率步進波形、隨機/偽隨機步進波形以及稀疏編碼波形等。典型的頻率稀疏編碼雷達波形如圖3所示[74]，其中，B為瞬時帶寬，Tsub為子脈沖寬度，Tp為脈沖寬度，其編碼序列為隨機編碼，通過設置脈內頻率編碼波形子脈沖頻率間隔大于子脈沖帶寬，雷達發射波形為頻率稀疏編碼信號。

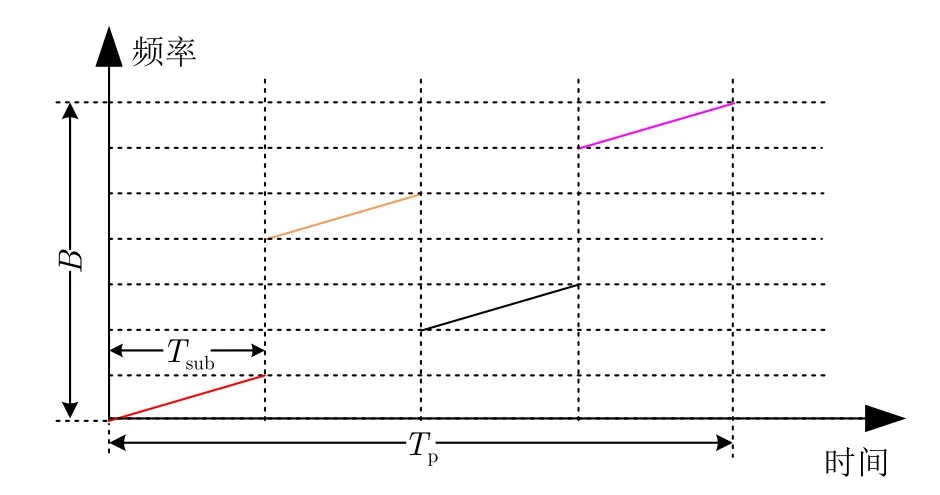
圖3 頻率稀疏編碼波形示意圖Fig.3 Schematic diagram of frequency encoded modulated signal

正交頻分復用(Orthogonal Frequency Division Multiplexing,OFDM)波形是一種多載波同時發射的波形，最初應用于通信系統中。1998年，Jankiraman等人將OFDM技術引入到雷達系統[75]。之后，Lellouch等人[76]首次將捷變思想與OFDM技術相結合，提出了頻率捷變-正交頻分復用(Frequency Agile Orthogonal Frequency Division Multiplexing,FA-OFDM)信號，而SFA-OFDM是在FA-OFDM的基礎之上發射稀疏子載波信號[77,78]。FA-OFDM波形示意圖如圖4(a)所示，在相參處理間隔的每個脈沖內發射多個頻點隨機跳變的子載波；如圖4(b)所示為SFA-OFDM，其在一個脈沖內發射連續的一組子載波，但是不同脈間的子載波組頻率稀疏，M為一個相干處理時間(Coherent Processing Interval,CPI)內的脈沖數，單個脈沖由K個帶寬為Δf的子載波組成，N表示總的跳頻數，N＞M，脈間最小跳頻間隔為B=KΔf，N個跳頻信號的總帶寬表示為Btotal=NB。

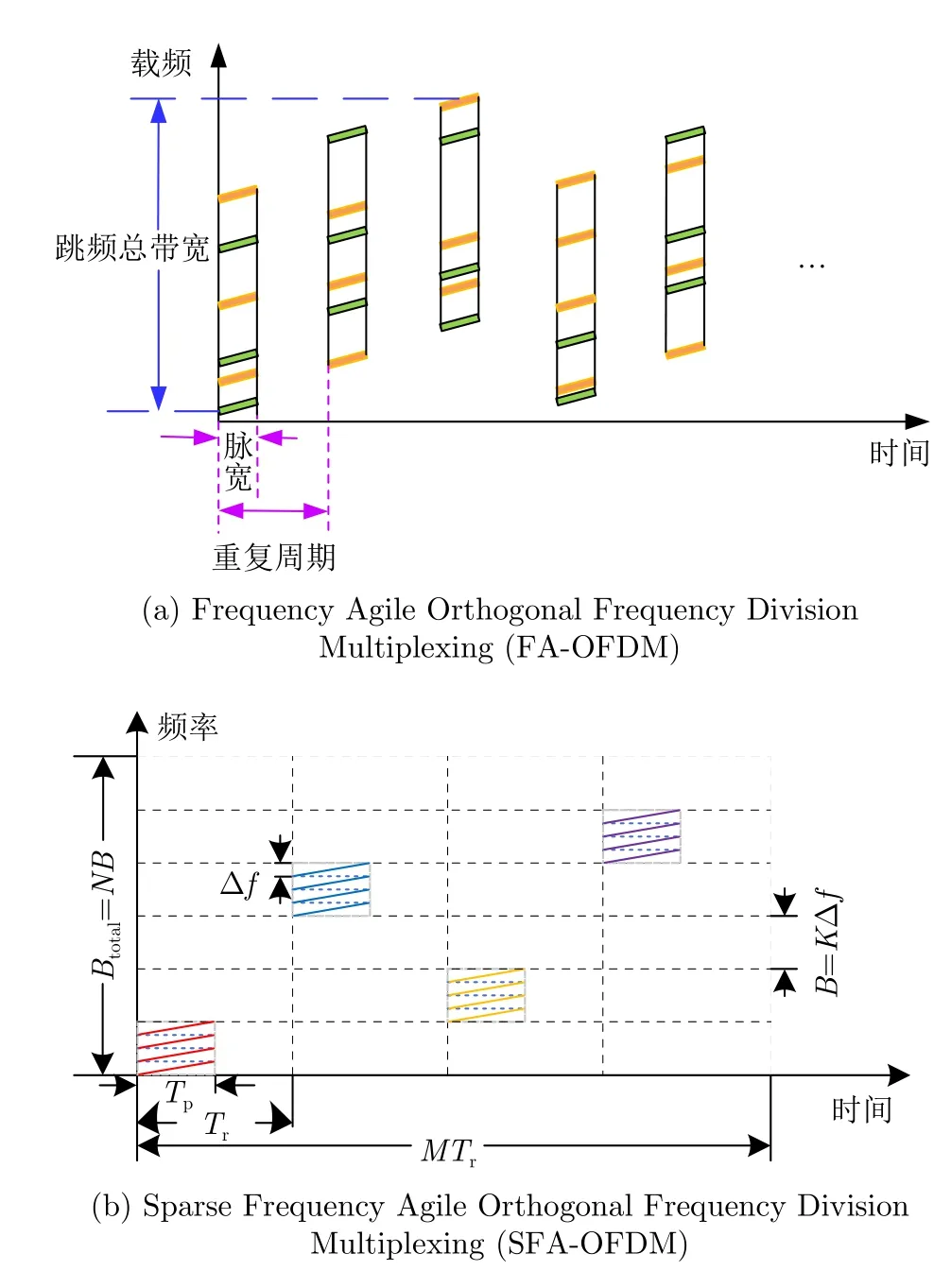
圖4 波形示意圖Fig.4 Schematic diagram of the waveform

(2) 空域稀疏雷達

空域稀疏雷達指的是雷達天線或者天線陣元的布陣方式存在稀疏性，雷達的天線布局設計以及雷達觀測方式都會導致空域稀疏的現象發生，典型的空域稀疏可分為稀布陣與孔徑稀疏兩種。

在相控陣列或數字陣列中，廣義的稀布陣指的是陣元非等間隔排布的陣列。在20世紀60年代至20世紀90年代，大量學者對稀布陣開展了研究[79-81]，現代的稀布陣可以分為稀布陣列與稀疏陣列兩種類別。兩者的區別在于陣元排布方式以及陣元間隔的不同[82]，稀布直線陣列陣元布局如圖5所示[83]，陣元數目為N，孔徑大小為 |dN-d1|，d1,d2,...,dN分別表示陣元的不同坐標，θ表示從線陣開始掃描的角度大小。稀布陣列的陣元排布方式以及陣元間隔是任意的，只是受限于互耦效應以及陣元自身的尺寸等因素的影響，陣元間隔限制大于等于半波長，且陣元間距是互相不能整除的。

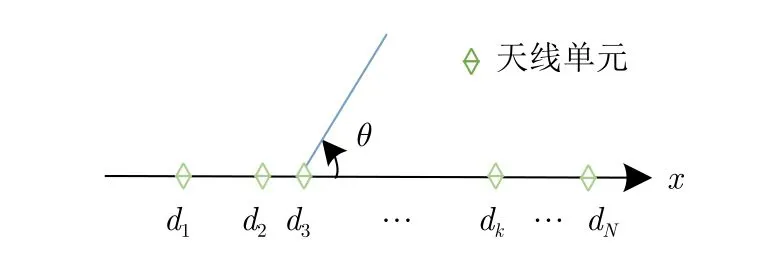
圖5 稀布直線陣列的幾何結構Fig.5 The geometry of the sparse linear array

稀疏直線陣列的陣元排布方式如圖6所示[83]，d為柵格間距，L=Md為孔徑大小，孔徑上有M+1個柵格點。稀疏陣列基于對均勻陣的采樣而形成的非均勻陣列，通過陣元的稀疏排布，各陣元間距為柵格間距的整數倍。稀疏陣列可以減小陣元之間的互耦效應，可以在陣列孔徑不減小的條件下，提高雷達分辨率[84]。

圖6 稀疏直線陣列的幾何結構Fig.6 The geometry of the thinned linear array

均勻直線陣列的陣元排布以及方向圖如圖7所示，圖7(a)為均勻直線陣列的陣元排布方式，圖7(b)為其相應的天線方向圖，此時的陣元排布為等間隔的10個陣元。

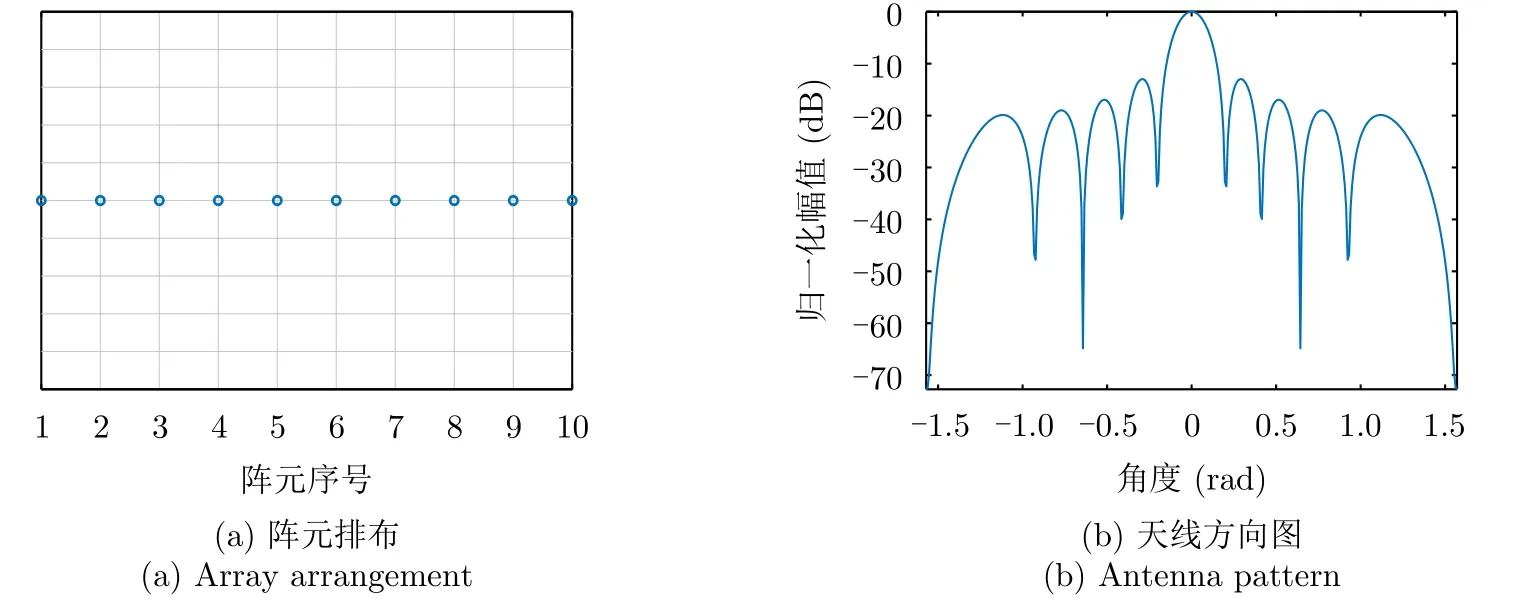
圖7 均勻直線陣列Fig.7 Uniform linear array

稀布直線陣列的陣元排布以及方向圖如圖8所示，陣元個數為8，圖8(a)為稀布直線陣列的陣元排布方式，圖8(b)為其相應的天線方向圖，稀布直線陣列的陣元排布更具有隨機性。

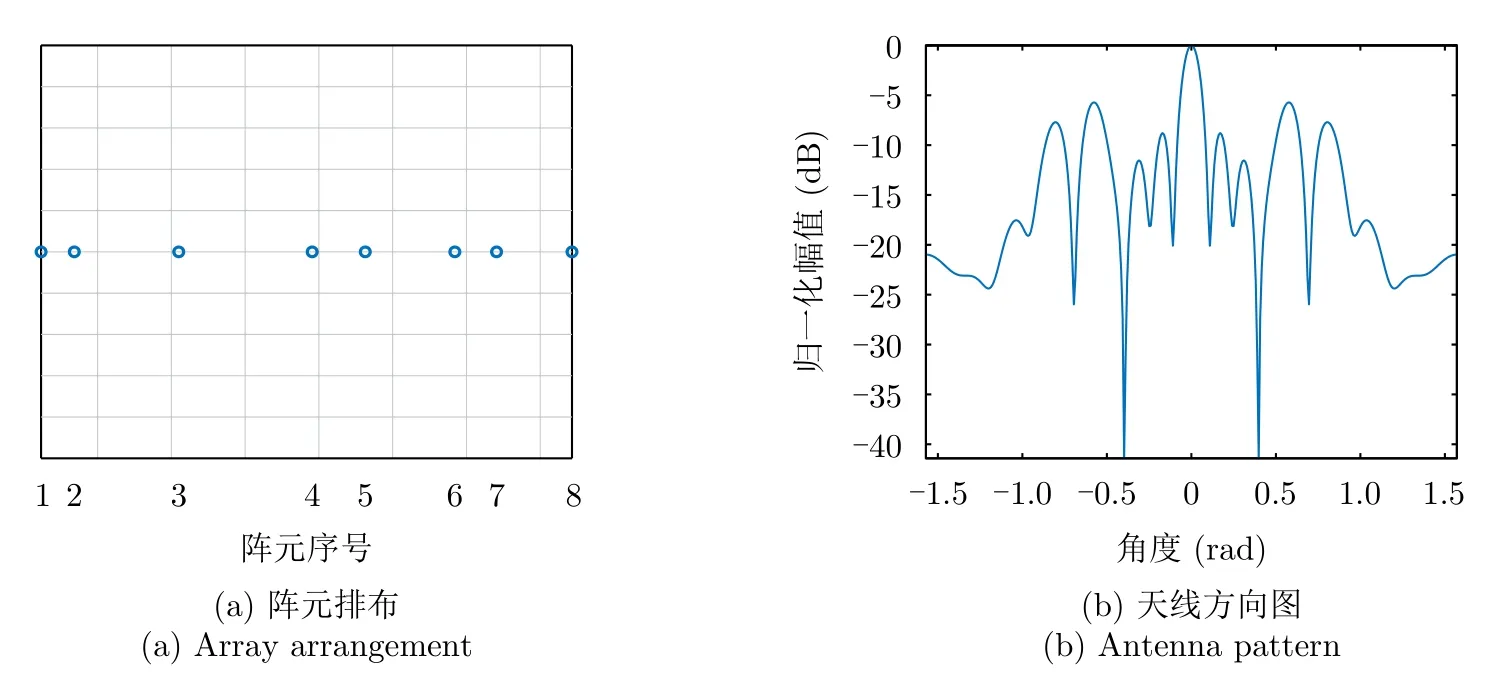
圖8 稀布直線陣列Fig.8 Sparse linear array

稀疏直線陣列的陣元排布以及方向圖如圖9所示，陣元個數為8，是在均勻直線陣列的基礎上對其進行采樣，圖9(a)為稀布直線陣列的陣元排布方式，圖9(b)為其相應的天線方向圖。

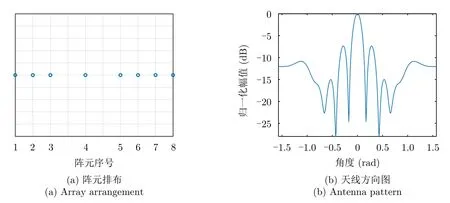
圖9 稀疏直線陣列Fig.9 Thinned linear array

稀疏孔徑是由于合成孔徑雷達觀測模式所帶來的一種特殊的空域稀疏。合成孔徑雷達通過對合成孔徑時間內的信號聯合處理，實現小孔徑天線合成大孔徑天線的效果，進而提升雷達的角度分辨率，但是隨著雷達同時多任務的功能需求以及相控陣等靈活波束指向技術的應用，合成孔徑雷達成像過程中雷達系統會分時執行不同的功能，從而導致對單一場景波束照射不連續或數據丟棄均會造成回波數據丟失，進而導致稀疏孔徑[85]。

4 稀疏恢復在雷達信號處理中的應用

雷達觀測場景中的先驗稀疏性與雷達的稀疏觀測方式為基于稀疏恢復的雷達信號處理提供了充分條件，本節結合傳統非稀疏體制雷達與新體制雷達中不同信號處理需求，圍繞空域處理、脈沖壓縮、相參處理、雷達成像以及目標檢測的典型雷達信號處理過程，對稀疏恢復技術在雷達信號處理中的應用展開討論。

4.1 空域處理

壓縮感知理論在空域處理的應用主要體現在空間譜估計、自適應波束形成以及陣列方向圖綜合等領域的應用。

在空域濾波應用方面，現有的方案主要是通過利用壓縮感知和稀疏表示技術對陣列采樣的相關矩陣進行更精確的估計，以此來提高和改善傳統方法的目標參數檢測性能[86]。針對傳統的多重信號分類算法估計信源數與陣列形式之間的矛盾，文獻[87]基于目標的空域稀疏性，采用OMP算法，在較少陣元數的條件下進行空間譜估計，并通過仿真進行驗證。針對空域信號波達方向(Direction of Arrival,DOA)估計中采樣數據量大以及受信噪比影響較大的問題，文獻[88]提出了采用奇異值分解的多矢量欠定系統的聚焦求解算法，基于空域目標信號占據少量角度分辨單元的稀疏性，實現了DOA高分辨估計。文獻[89]提出了一種基于深度展開交替方向乘子法(Alternating Direction Method of Multipliers,ADMM)網絡的離格DOA估計方法，可在提高估計精度的同時降低計算復雜度。針對空時自適應處理(Space-Time Adaptive Processing,STAP)，利用稀疏恢復技術可以通過極少的樣本估計雜波空時譜，有效降低STAP的運算復雜度。為了在小訓練樣本場景下提高雜波抑制性能，文獻[90]基于稀疏約束投影近似子空間跟蹤，提出了一種快速STAP算法。利用雜波協方差矩陣的低秩特性，在投影近似子空間跟蹤的代價函數中施加稀疏約束，迭代推導出自適應權向量，與沒有稀疏約束的傳統STAP方法相比較，該方法具有更好的性能和更快的收斂速度。大多數基于稀疏恢復的空時自適應處理技術都受到角度多普勒平面離散化引起的離網效應的影響?？哲婎A警學院王永良團隊[91]提出了一種利用雜波脊先驗信息劃分非均勻網格的稀疏恢復-空時自適應處理(Sparse Recovery Space-Time Adaptive Processing,SR-STAP)方法，并證明了采用非均勻字典的SR-STAP算法后的雜波抑制性能優于傳統的均勻字典。針對大規模字典應用，Cui等人[92]提出了一種基于張量的稀疏恢復空時自適應處理方案，傳統的基于向量的運算被其相應的低復雜度張量表示取代，使得一個大規模的矩陣運算轉化為多個小規模的矩陣計算，從而可以在恢復過程中節省巨大的運算量。

稀疏陣列由于陣元的稀疏性，通過少量陣元可以滿足設計指標要求，同時降低成本。文獻[93]提出了一種新的陣列稀疏方法，基于壓縮感知理論求取稀疏線性陣列方向圖，并驗證了該方法在少量稀疏陣元實現低增益、強方向性的方向圖效果的有效性。文獻[94]構建了一個統一的空頻域稀疏模型，可以同時估計載波和DOA，結合多傳感器數據進行頻譜重構，提高數據利用率和DOA估計精度，并通過頻譜和DOA的時空分布特性解決了陣列參數估計中的源模糊和相干信號問題。同時根據信號空間分布的稀疏性特征，給出了一種空間分離處理方案，從而顯著降低計算復雜度。另外，該方法放寬了對陣列流形的限制，適用于任意陣列，具有更廣闊的應用前景，仿真和硬件結果驗證了該方法的有效性。稀疏陣列的自由度可以利用無網格算法實現，可實現在避免網格劃分的同時，恢復虛擬陣列空洞的響應[95]。文獻[96]針對均勻/稀疏線性陣列的DOA估計問題，提出了一種基于協方差擬合準則的稀疏參數法，實現了在無網格的劃分的同時實現DOA參數估計。

近年來，多任務貝葉斯壓縮傳感(MulTitask Bayesian Compressive Sensing,MT-BCS)已成功應用于單模式稀疏平面陣列的合成，在文獻[97]中，Yu等人把MT-BCS擴展到多平面陣列方向圖的合成，實現了在較短的時間內解決大規模陣列問題，并獲得相對稀疏的結果。根據稀疏陣列場景信息，可構建如下模型[84]：

其中，X是陣列接收信號，S是空間目標角度位置，S中只有有限個元素是非零的，N是噪聲，A表示場景感知矩陣，f(·)為場景關系函數。

雜波及干擾場景下，為提升空間角度超分辨性能通過對弱小目標角度位置進行加權來區分目標、噪聲及干擾區域，則在目標角度求解過程中既能保證散射中心的恢復精度又能抑制噪聲和干擾，結合稀疏表示與?1,?2分解方法，稀疏陣列角度超分辨壓縮感知模型如下所示：

其中，W表示加權矩陣，gw(·)表示加權矩陣W與空間角度位置S之間的關系函數。利用稀疏信號處理技術對式(10)進行迭代求解，可獲得空間角度超分辨結果。

基于上述的壓縮感知模型，設置10×10陣面，50個陣元的稀布陣，空間角度分辨率為 11.5°，稀疏陣的排布如圖10所示。在單快拍場景下，將初始角度分辨結果與OMP算法[4]進行比較，對比結果如表1及圖11所示。圖11(a)為初始角度分辨結果，圖11(b)為通過OMP算法得到的空間角度超分辨結果。依據表1所示的誤差分析結果以及圖11所示的仿真結果對比，可以看出初始角度分辨結果分辨率較低，采用OMP算法可實現角度超分辨，但是存在一定的誤差。

表1 計算結果對比圖Tab.1 Comparison chart of calculation results

圖10 陣面陣元位置分布Fig.10 Distribution of array element locations

4.2 脈沖壓縮

基于匹配濾波理論，線性調頻信號是應用最廣泛的一種脈沖壓縮信號。窄帶雷達脈沖壓縮處理中，通常利用匹配濾波實現。寬帶雷達通常采用有源相關處理實現脈沖壓縮，進而得到目標散射點的高分辨一維距離像。傳統的脈沖壓縮為了降低旁瓣需要進行加窗處理，但是加窗處理會存在主瓣展寬的現象[98,99]；同時常規脈沖壓縮的距離分辨率取決于信號的帶寬，而基于目標場景的稀疏性，利用壓縮感知可以實現對目標距離的高分辨。

相關學者開展了基于稀疏恢復思想實現脈沖壓縮的研究，文獻[37]針對大帶寬信號傳輸數據量大的問題，結合SAR雷達系統的脈壓工作機理，在降低距離像數據量的同時，基于脈壓后距離上的強點稀疏性，運用壓縮感知理論實現脈沖壓縮；同時，與傳統的匹配濾波方法進行對比，文獻[37]表明壓縮感知方法得到的脈壓結果更加理想的旁瓣。文獻[98]針對傳統脈沖壓縮低旁瓣與主瓣展寬的矛盾，提出了一種基于壓縮感知的線性調頻(Linear Frequency Modulation,LFM)脈沖壓縮的實現方法，構造與脈壓參考信號相關的稀疏基，利用平滑最小化0-范數算法，在保留回波信號的相位信息的同時對脈壓結果實現了較高精度重構。文獻[100]分別對匹配濾波以及去斜處理進行介紹，針對匹配濾波模式下的壓縮感知距離壓縮算法，通過對雷達作用距離范圍進行網格劃分，對發射信號進行延時構造稀疏基矩陣，將觀測值以及重建矩陣代入重構算法，實現匹配濾波的脈壓結果重構；針對去斜模式下的壓縮感知距離壓縮算法，稀疏矩陣為單位矩陣的傅里葉逆變換，稀疏恢復之后去除剩余相位，繼而得到一維距離像。文獻[101]針對寬帶LFM信號的脈沖壓縮處理，首先對其進行去斜處理，基于去斜回波信號的頻譜稀疏性，采用正交匹配追蹤算法重構了目標回波的一維高分辨距離像。假設雷達的發射信號為

Tp代表脈沖寬度，t代表快時間且滿足 0＜t＜Tp，φ(t) 為脈沖內的信號調制，rect(·)表示矩形窗函數。

假設場景中有G個目標，τg表示第g個目標的延時，則混頻后的雷達回波信號表示為

混頻后對雷達回波數據采樣得到s，K為稀疏基，H為量測矩陣，ζ為噪聲項，ω為待求解脈壓結果，則壓縮感知模型可以表示為[98,99]

分別采用傳統脈沖壓縮算法以及正交匹配追蹤算法對頻率編碼信號進行脈沖壓縮。如圖12所示，仿真場景中存在3個點目標時，目標形成的強幅值點在距離單元上呈現稀疏性，圖12(a)為頻率編碼信號做傳統脈沖壓縮結果，可以看出此時的旁瓣較高，主旁瓣比為14 dB；采用正交匹配追蹤算法實現脈沖壓縮時，如圖12(b)所示，此時脈壓結果相較于傳統方法旁瓣明顯降低，但是相近的兩個點目標之間存在一定的旁瓣。

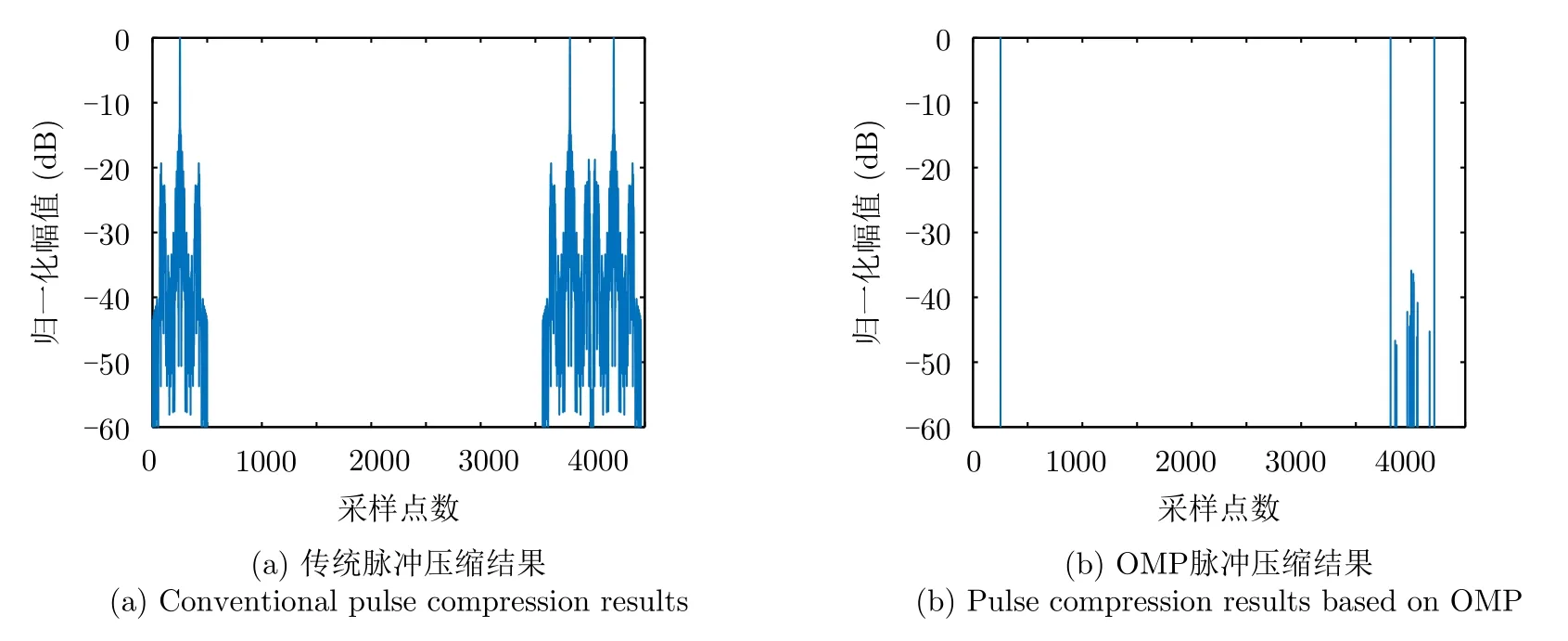
圖12 傳統算法與OMP算法的脈沖壓縮結果Fig.12 Comparison of pulse compression results based on traditional algorithm and OMP algorithm

4.3 捷變相參處理

當雷達探測場景目標個數稀疏時，對目標回波進行脈沖壓縮之后，一個粗分辨距離單元中往往只有有限個目標，因此一個粗分辨距離單元中的目標呈現出高分辨距離域、速度域或者距離-多普勒等聯合特征域的稀疏分布，通過構造與目標特性相符的字典矩陣，利用壓縮感知算法可實現對有限個目標的距離以及多普勒等信息的估計。

稀疏恢復在新體制雷達的相參處理方面的應用是稀疏信號處理的研究熱點，被廣泛應用于比如隨機脈沖重復頻率(Pulser Repetition Interval,PRI)抖動、脈間捷變、載頻-重頻聯合捷變等雷達的相參處理中，由于重頻抖動與頻率捷變雷達可視作載頻-重頻聯合捷變雷達的特例，假設雷達觀測場景中存在G個目標，每個目標相對雷達的徑向距離和徑向速度分別表示為rg和vg，其中g ∈{1,2,...,G}為目標個數索引，Tq為慢時間序列，將第q個發射脈沖的載頻為fq，fq=f0+d(q)Δf，其中 Δf為最小跳頻間隔，f0為基準載頻，d(q)是頻率跳變編碼，d(q)∈{1,2,...,N}，N為總跳頻點數，則第q個脈沖壓縮后的載頻-重頻聯合捷變回波信號表示為

其中，Tr代表平均脈沖重復頻率，Tr/U(q)第q個脈沖的隨機抖動程度。

根據探測場景稀疏性，構建壓縮感知信號模型[102]：

其中，δ為噪聲向量，S為對回波信號采樣后做脈沖壓縮處理的數據，Z為冗余字典矩陣，通過將雷達不模糊距離以及不模糊速度區間進行劃分，使得字典矩陣中包含目標的距離以及速度信息，θ為待重構的相參結果。

基于場景稀疏性，利用字典矩陣和脈壓數據可重建向量θ。然后，通過求解一個?1范數最優問題對原始信號進行重構：

噪聲項ε=‖δ‖2可以從相鄰的距離/速度單元估計。

相對于固定參數脈沖多普勒(Pulse Doppler,PD)雷達而言，脈間捷變雷達的目標回波的脈間相位由線性變化轉為非線性變化，如圖13所示，圖13(a)為PD雷達相位的脈間相位，圖13(b)為脈間頻率捷變雷達的脈間相位，可以看出脈間捷變雷達的相位在脈沖間非線性變化，這種變化使得傳統動目標檢測(Moving Target Detection,MTD)信號處理算法不再適用，基于場景的稀疏性先驗信息，壓縮感知技術被引入到捷變波形的相參處理中，實現了多脈沖聯合處理并完成了目標的參數估計。

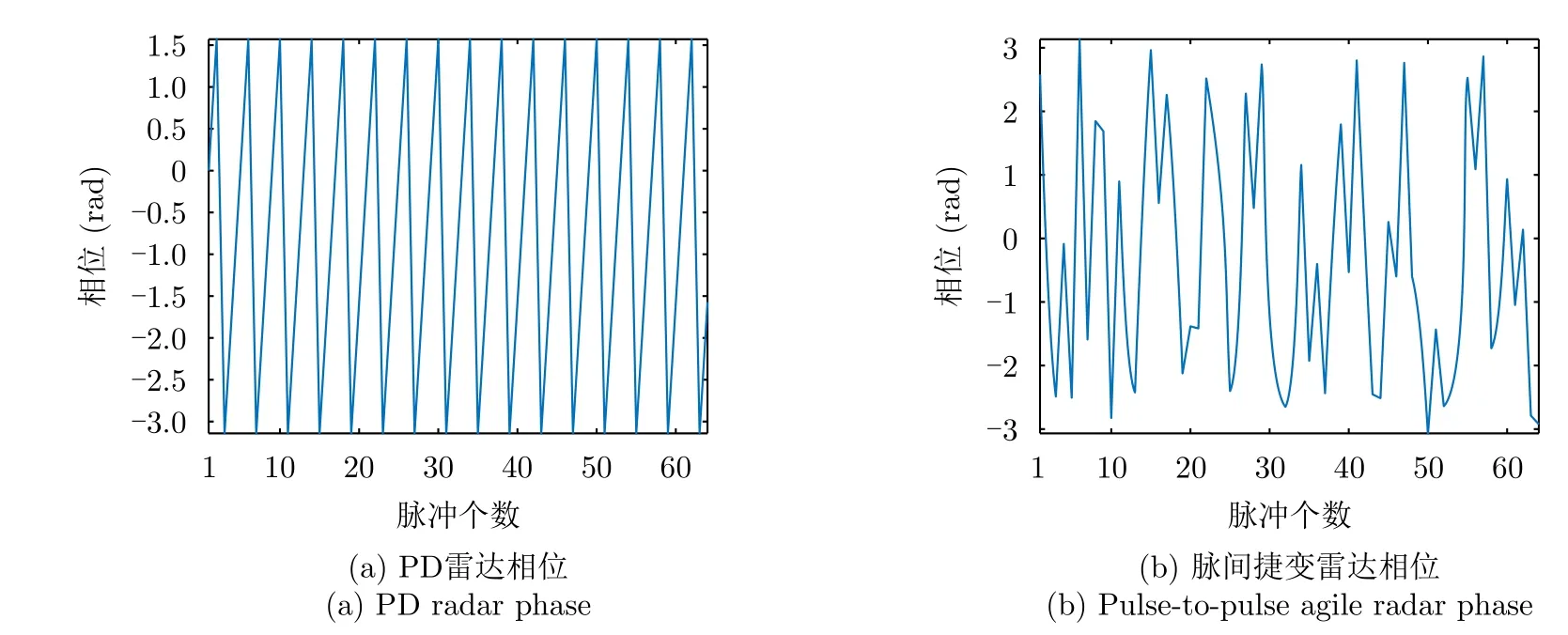
圖13 PD雷達與脈間捷變雷達相位Fig.13 Radar and pulse-to-pulse agile radar phase

在隨機PRI抖動雷達的信號處理問題方面，稀疏恢復主要被應用于多普勒參數提取與解模糊等應用，文獻[103]提出了基于稀疏恢復的重頻抖動雷達解模糊算法，并基于加權稀疏重構的方法實現了對雜波的抑制。文獻[104]針對假目標場景下變重頻雷達稀疏性被破壞的問題，提出了目標與干擾聯合稀疏表征的處理方法。

在頻率捷變的相參處理方面，基于稀疏恢復的算法在目標距離-速度二維信息重建、邊界性能分析等方面取得了豐碩的研究成果。文獻[45]基于目標稀疏性，利用壓縮感知算法對稀疏步進頻信號實現目標參數估計。文獻[72]針對距離-速度聯合匹配中的網格失配問題，提出了總體最小二乘的自適應匹配追蹤算法。清華大學劉一民團隊[57,105]對基于稀疏恢復的捷變相參能力邊界進行分析與討論，給出了場景中目標以及雜波個數K的邊界，文中指出當(N為脈沖個數，M為載頻個數)時，觀測場景可大概率被精確重構，進一步地，通過相變圖對其性能邊界進行表征。在脈間頻率捷變的基礎之上，對于脈間的載頻-重頻聯合捷變波形的相參處理方面，文獻[106]結合載頻與重頻跳變序列，在脈沖壓縮之后構建了與目標高分辨距離-速度信息相匹配的二維字典矩陣，利用OMP實現對目標距離-速度的二維重構。本文結合構建的壓縮感知模型，采用OMP算法對脈間捷變雷達進行相參處理[106]，并與快速傅里葉變換(Fast Fourier Transform,FFT)算法進行對比，結果如圖14(a)所示，由于脈間相位的非線性變化，傳統相參處理算法失效，無法完成目標的多普勒測量；如圖14(b)與圖15(a)所示，OMP算法可對脈間捷變雷達實現有效相參處理，但是采用此種方法進行相參處理時，會存在網格失配的問題，如圖15(b)所示，當目標的距離與速度并不在所設的距離-速度網格上時，存在失配問題。

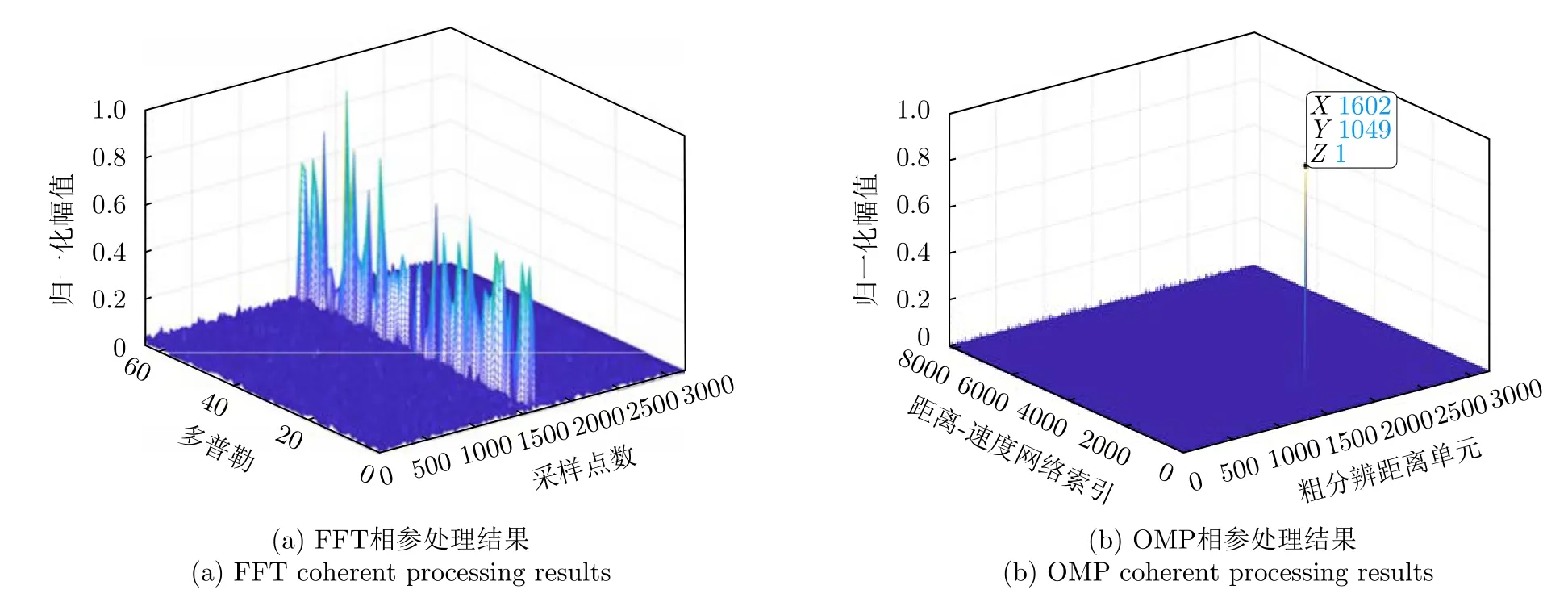
圖14 FFT算法與OMP算法Fig.14 FFT algorithm and OMP algorithm

圖15 目標所在距離單元的重構結果Fig.15 Reconstruction results for the distance cell where the target is located

在SFA-OFDM波形的相參處理方面，文獻[71]針對SFA-OFDM波形的目標參數估計問題，提出了通過對多子載波的壓縮感知處理等效合成寬帶OFDM，利用目標在距離-速度聯合特征域的稀疏性，基于壓縮感知對距離-速度高分辨進行估計。文獻[78]通過對子載波頻移、時移等的操作，將SFA-OFDM波形的相參處理問題轉換為捷變雷達的相參處理問題，結合目標場景稀疏性，實現對目標的距離-速度的高分辨估計。

4.4 雷達成像

雷達成像是指對發射的電磁信號的回波進行信號處理，從而得到感興趣的目標的電磁散射特性信息[107-109]。如3.2節所述，雷達成像回波存在的數據缺失現象會導致孔徑稀疏問題，本節對壓縮感知成像模型以及稀疏信號處理在SAR與ISAR中的應用展開討論。

不失一般性地，合成孔徑雷達成像觀測可表示為[110]

其中，σ(x,y) 表示位于 (x,y)的目標的后向散射，具有隨機相位。c表示電磁波速度，f表示載波頻率，τ和t分別表示對應距離和方位向的快慢時間。u(τ)表示發射信號的包絡。將散射場分解為二維離散網格，并以矢量形式疊加，得到離散化后的觀測模型為[110]

其中，s表示采樣后的回波數據，x表示待求解的成像結果，表示n噪聲，F表示SAR成像過程對應的觀測方程，Ψ表示稀疏采樣。

壓縮感知稀疏成像利用稀疏先驗實現對x的重建。對ISAR而言，目標相對背景具有天然的稀疏性，對SAR而言，即使x本身不具備稀疏性，也可利用線性變換x=Φa挖掘其在變換域的稀疏性，因此壓縮感知成像模型可統一表示為

其中，‖a‖p表示向量的?p范數，ε表示估計的噪聲誤差。

(1) 壓縮感知SAR成像

傳統的雷達成像方法在數據大量缺失條件下，存在高旁瓣以及高柵瓣的問題。將壓縮感知應用到高分辨雷達成像中，基于雷達成像場景的先驗稀疏性，可以從少量的測量數據中重構目標圖像，有效緩解數據采集、存儲等的壓力[111]，解決不完整采樣條件下的稀疏孔徑雷達成像問題。2007年，Baraniuk等人[18]提出了一種低采樣率的SAR系統，并通過實驗驗證了欠采樣條件下獲取目標高分辨圖像的能力。在此之后，稀疏信號處理技術被逐步應用于單基SAR和多基SAR的信號處理中。

在單基地SAR信號處理方面，壓縮感知成像技術的研究集中在稀疏孔徑條件下高質量成像技術以及性能邊界分析等方面。文獻[48]提出一種基于CS理論的SAR成像方法，該方法同時在距離維和方位維進行CS反演，在大量原始數據被丟棄的條件下，具備良好的二維成像效果。后續相關學者對成像稀疏表示以及壓縮感知理論在不同的成像場景中的應用等方面展開了研究。文獻[112]基于小波稀疏表示的SAR成像方法，對隨機稀疏采樣的數據進行處理，實驗結果表明在方位向數據嚴重降采樣的條件下，采用所提算法可以無模糊重構SAR圖像。針對聚束SAR成像問題，文獻[113]構建了基于CS的成像模型，采用交替迭代思想求解優化問題，實現了目標圖像特征增強，同時對有限數據量的目標成像具備魯棒性。文獻[114]通過聯合稀疏正則化以及卷積神經網絡(Convolutional Neural Network,CNN)，設計了一種即插即用框架，實現了聚束式SAR成像。文獻[115]將成像自聚焦問題視為一個聯合優化問題，在變分最大化期望準則下提出一種聯合相位誤差抑制的稀疏成像算法，該算法充分利用相位噪聲的先驗特性以及目標的結構稀疏散射特性，實現了精度較高的相位噪聲估計和聚焦良好的成像結果。如圖16所示，SAR數據稀疏孔徑情況下，由于稀疏孔徑導致了多普勒模糊，傳統SAR成像結果存在散焦和模糊問題，利用壓縮感知[116]能夠從稀疏孔徑數據重建無模糊SAR圖像，但是采用壓縮感知技術重構SAR圖像時，需要滿足稀疏性要求，且使用壓縮感知技術時需要考慮運算量的問題。

圖16 傳統SAR成像算法與壓縮感知稀疏成像結果Fig.16 Comparison of SAR imaging results based on traditional algorithm and CS algorithm

多基地雷達系統相較于單基地雷達系統具有更強的靈活性，可從多角度觀測獲得更多目標信息，但是由于雷達系統接收信息的增加，也意味著雷達系統有更大的數據存儲壓力。壓縮感知理論的應用可以有效解決多基地雷達數據量大以及高分辨能力與雷達系統成本之間的矛盾[117]。文獻[118]研究了CS理論在多站SAR場景下運動目標成像問題，并通過仿真說明了壓縮感知方法比傳統通過匹配濾波方法在自聚焦方面具有更好的性能。文獻[119]針對雙基地SAR二維高分辨成像問題，將CS理論與雙基地SAR模型相結合，測量值采用二維隨機降采樣回波數據，與傳統的雙基SAR成像算法相比，基于CS的重建算法具有更高的分辨率，且數據量更少。

(2) 壓縮感知ISAR成像

與在SAR中的影響相似，稀疏信號處理技術也用于解決稀疏孔徑條件下的ISAR成像處理。通過對實測數據進行隨機稀疏采樣后，采用基于?1范數的壓縮感知(L1-norm CS,L1-CS)算法[120,121]得到不同信噪比下的ISAR成像結果如圖17所示，可以看出L1-CS算法可以在稀疏孔徑條件實現ISAR成像，但是其成像性能會受到信噪比的影響。利用均方根誤差(Root Mean Square Error,RMSE)以及相關系數(Correlation Coefficient,CORR)作為ISAR成像性能評估指標，給出不同稀疏孔徑數據條件下的成像性能評估結果，結果如圖18以及表2所示，隨著稀疏采樣率的提升，L1-CS算法的均方根誤差逐漸減小，相關系數逐漸提升[121]。本小節結合平穩目標的ISAR成像與機動目標ISAR成像兩種場景，對稀疏信號處理在ISAR成像中的應用展開討論。

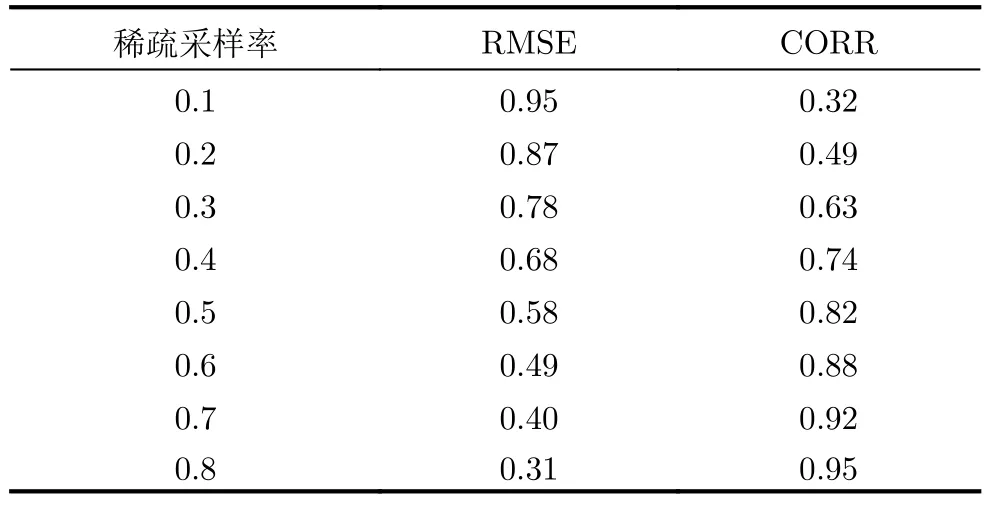
表2 成像性能分析Tab.2 ISAR imaging performance analysis

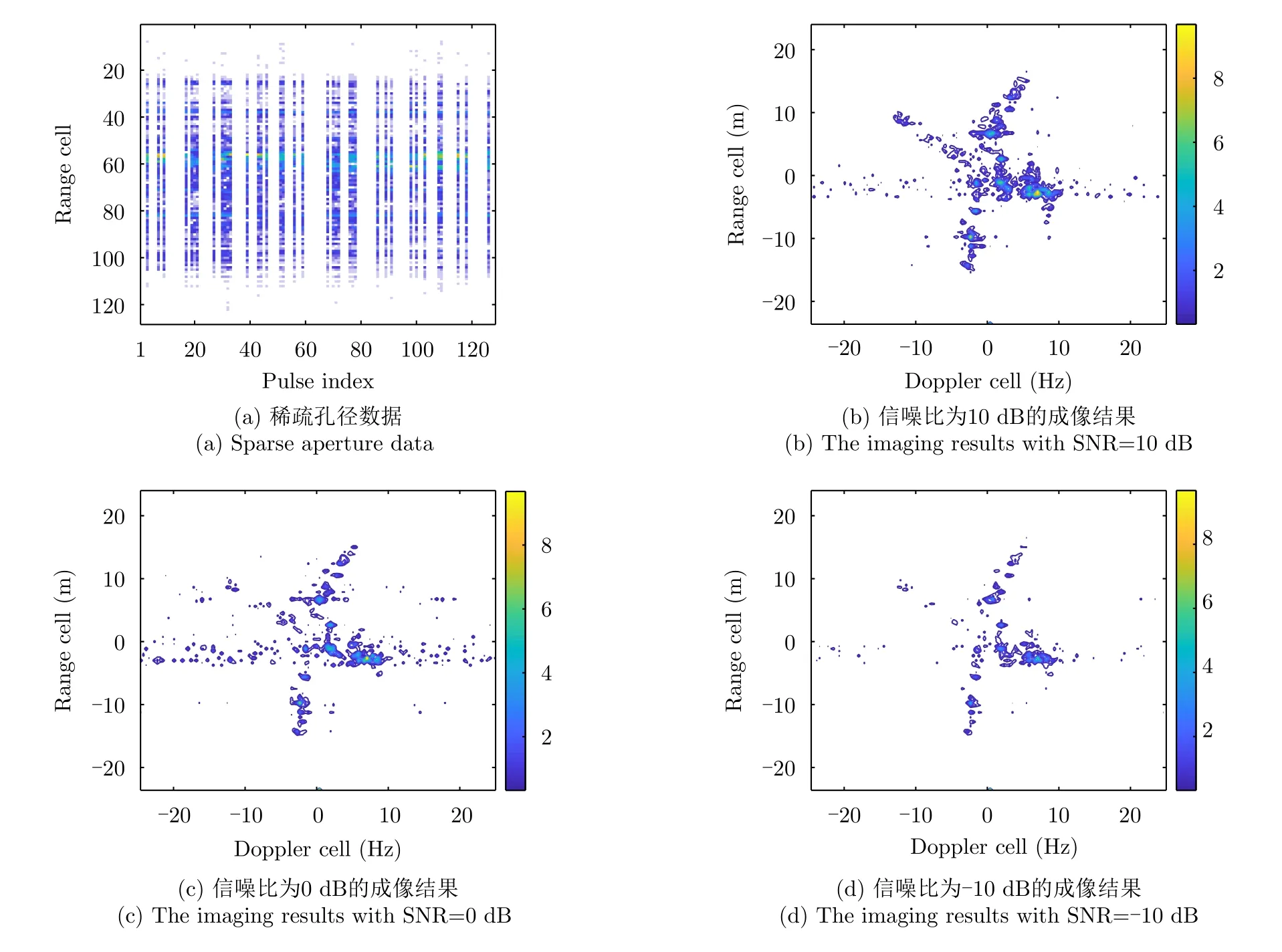
圖17 稀疏孔徑下的稀疏ISAR成像[120]Fig.17 Sparse ISAR imaging using sparse aperture[120]

圖18 ISAR成像性能分析[121]Fig.18 ISAR imaging performance analysis[121]

在平穩目標的ISAR稀疏成像方面，西安電子科技大學邢孟道團隊[122]利用CS實現了對目標的超分辨ISAR成像，進一步通過相干投影和加權提高了算法的抗噪以及抗雜波性能，完成對散射中心的精確估計。對于低信噪比場景，文獻[123]提出了基于廣義柯西分布族中Meridian先驗的CS超分辨成像模型。隨著脈沖數量和信噪比的降低，該模型在分辨率和幅度誤差方面相較于基于拉普拉斯先驗的CS模型表現出更好的性能。在雜波場景中，為解決信號與雜波背景難以區分問題，文獻[124]結合局部稀疏約束和非局部總變分提出了新的ISAR成像方法，該方法去除虛假的強散射中心或雜波的同時保持了目標區域的形狀和幾何結構，減少虛假散射點和雜波對ISAR成像的影響。針對欠采樣ISAR成像問題，文獻[125]提出了一種基于ADMM展開網絡成像算法，基于多個可學習的稀疏變換以及可學習的逐點分段線性函數，實現了欠采樣條件下的高性能ISAR成像。此外，大量學者開展了相位誤差校正方面的研究工作[126]，提高了 CS 成像算法的魯棒性。

機動ISAR目標的回波信號在一定匹配傅里葉域具有稀疏性，文獻[127]提出了適用于隨機稀疏孔徑和短孔徑情況的基于壓縮感知的ISAR成像方法，該方法考慮了稀疏字典對相對旋轉參數的依賴性，并利用分數傅里葉域最優搜索的參數估計方法實現參數估計，實現了良好的成像效果。文獻[128]利用目標場景的稀疏空間特性來描述其在時頻域中的回波信號的稀疏性，構建基于瞬時傅里葉變換的字典并將距離-瞬時多普勒(Range-Instantaneous Doppler,RID)成像轉化為稀疏重建問題，然后采用迭代加權策略實現信號增強和噪聲抑制。

4.5 雷達目標檢測

在現代雷達通常采用恒虛警率(Constant False Alarm Rate,CFAR)進行目標檢測，在雜波或者存在干擾的場景中CFAR的檢測門限會隨著參考單元變化而自適應改變，從而完成恒虛警目標檢測。CFAR作為一種經典的目標檢測方法，其理論研究與工程應用方面均得到了不斷的發展與完善[129]，但為了減小雷達處理數據量，將壓縮感知運用在CFAR中成為一種研究趨勢，在拓展目標檢測等應用中取得了廣泛應用。假設雷達系統發射信號為步進頻，第q個脈沖串經過鑒相器后的輸出表示為[130]

其中，R和v分別表示目標的距離和速度，c為光速，fq為第q個回波信號的載頻，T為雷達發射信號的脈沖重復周期。根據壓縮感知理論可將鑒相器的輸出改寫成矩陣的形式：

隨機抽取Ψ中的n行作為觀測矩陣，該過程可描述為

n′是復高斯噪聲。將式(23)轉化為以下無約束問題：

其中，λ表示松弛因子。

目前基于壓縮感知框架實現目標檢測方面的研究成果頗多，文獻[131]通過設計一種建立在壓縮域上的分布式單元平均恒虛警(Cell Averaging-CFAR,CA-CFAR)檢測器和適用于壓縮檢測的門限選定方法，可在低SNR下直接實現目標檢測，無需重構，節省了運算量。另外，基于壓縮感知將CFAR與其他算法聯合也有優異的性能，文獻[132]針對基于壓縮感知的CA-CFAR檢測器在相近目標檢測性能下降的問題，提出了一種基于壓縮感知的可變標識恒虛警檢測算法(Compressive Sensing Variable Identification-CFAR,CSVI-CFAR)；清華大學劉一民團隊[133]針對行正交設計模型下壓縮感知傳感器的目標檢測問題，提出了一種去偏LASSO檢測器的設計，相較于傳統的壓縮感知檢測器和其他去偏的LASSO檢測器而言，該檢測器可以根據給定的誤報率進行分析提供閾值且具有更優的檢測性能。文獻[134]基于壓縮感知理論，分析高分辨率范圍剖面(High Resolution Range Profile,HRRP)可以通過?1范數最小化從低維壓縮感知測量中獲取，利用統計特性和顯性散射體，提出一種新的恒虛警檢測器來檢測復高斯噪聲中的距離擴展點目標。

5 結語

將雷達場景中的稀疏性作為目標參數估計與雷達成像的約束條件，可以有效提升傳統雷達信號處理的性能，或者解決新雷達體制下傳統信號處理方法不適用的問題，因此稀疏信號處理技術在雷達數字信號處理的各個階段都得到了廣泛的應用。隨著雷達技術的不斷發展，新的雷達體制、雷達系統設計、雷達觀測方法也層出不窮，美國國防高級研究計劃局也推出了其超線性信號處理的雷達發展項目，擬在通過雷達信號處理的方法提升雷達在硬件受限條件下的探測能力，信號稀疏表示法也被視作其中的重點處理技術?？偠灾靡嬗诶走_探測場景中的稀疏先驗條件，稀疏信號處理將雷達信號處理技術的發展中繼續發揮持續而深刻的作用。

利益沖突所有作者均聲明不存在利益沖突

Conflict of InterestsThe authors declare that there is no conflict of interests