抗滑樁極限位移及樁側阻力分布型式研究

周喜武 朱俊高 包騰飛 陳學東 顏 韜 董云鵬

(1.江蘇省水利工程科技咨詢股份有限公司, 南京 210029;2.河海大學 巖土力學與堤壩工程教育部重點實驗室, 南京 210098;3.河海大學 水利水電學院, 南京 210098;4.三峽大學 水利與環境學院, 湖北 宜昌443002;5.河海大學 大禹學院, 南京 210098;6.東北農業大學 水利與土木工程學院, 哈爾濱 150030)

工程中常利用樁的側承載能力加固岸坡,提高岸坡的抗滑穩定性,這類樁稱為抗滑樁,它是提高岸坡穩定性最有效的工程構筑物.在設計抗滑樁時,需根據岸坡的穩定狀況、抗滑樁抗滑阻力大小及分布型式確定樁徑、樁間距及樁長等.國內外對抗滑樁樁側阻力的計算方法及其分布型式已有一些研究,王龍等[1]基于極限分析上限原理和擬動力法,考慮基質吸力對樁側阻力的提升作用,分析了樁間距、樁位布置及土體內摩擦角對岸坡加固效果的影響.余敏林[2]基于強度折減法,分析了抗滑樁樁長及樁間距對岸坡穩定的影響.李仁平[3]通過分析黏性土體中抗滑樁與土體之間的作用關系,提出了采用理想彈塑性模型計算樁側土壓力.魏作安等[4]采用彈性理論方法分析了樁后土體應力的分布.戴自航等[5]采用三維有限元法對樁周土壓力的分布規律進行了研究.咸玉建等[6]采用有限元法,分析了抗滑樁極限滑坡推力的大小和分布.以上研究成果對抗滑樁抗滑阻力及樁側阻力分布型式的確定有一定的指導作用,但在適用范圍及計算精度等方面尚有改進的余地.

筆者曾采用有限元法分析了抗滑樁極限阻力的影響因素,給出了樁極限阻力的計算模型[7].但對于抗滑樁的極限位移,目前尚未有系統研究.圖1為采用黏土進行試驗所得到的樁阻力F與樁位移X的關系曲線.本文將抗滑樁達到極限阻力Fu時所對應的樁位移Xu定義為抗滑樁的極限位移.

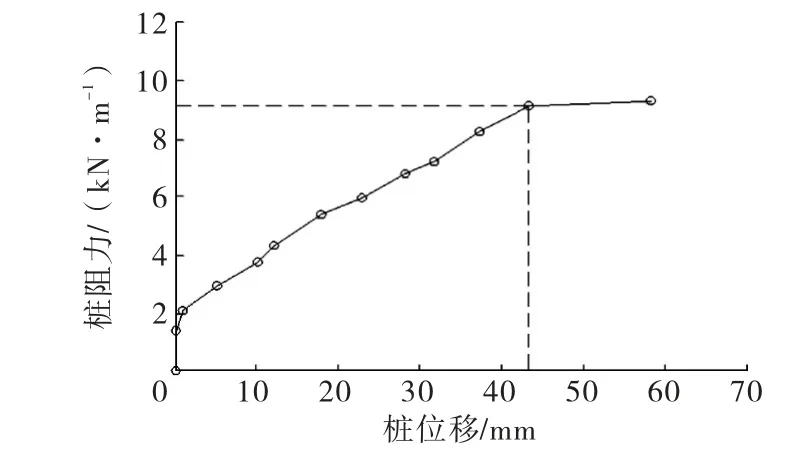
圖1 樁阻力與樁位移的關系曲線

對于地基中的抗滑樁,一般可以通過量測樁的變位來判斷該樁是否正常工作[8].由樁的極限位移Xu的定義可知,當樁土相對位移X大于Xu時,就可以判定該樁基礎是不安全的.通過本文的研究發現,在樁的不同深度處,樁的極限位移Xu是不同的,Xu是隨樁埋置深度的增加而增大的.這也說明在通過量測樁土的相對變位來判斷該樁是否正常工作時,僅量測樁頂變位是不夠的,而應該從土層所埋置的樁身段整體來考慮.

另外,對于某些結構,在實際使用時不允許產生過大的變位,即實際使用時樁土之間的相對位移可能達不到樁的極限位移,因此樁周土體對樁所提供的阻力也就達不到極限阻力.如果確定了樁周土體不同深度處樁的極限位移,就可以根據實際結構所允許的變位來計算各深度樁周土體所能提供的最大阻力,并進一步確定樁側阻力的分布型式,從而使抗滑樁的設計更合理.因此,研究抗滑樁的極限位移,無論是對地基中抗滑樁變位安全監測還是對確定樁側阻力的分布型式,都具有一定的意義.本文將采用有限元法研究抗滑樁極限位移的影響因素,給出樁極限位移的計算模型及樁側阻力分布型式,可供實際工程參考.

1 有限元模型及樁、土體參數

1.1 有限元模型

由于抗滑樁樁周土體主要沿水平向對垂直樁作相對運動,而在沿樁深度方向變形很小[9].因此,可以假定在深度方向上,土層處于平面應變狀態.基于這種假定,本文采用河海大學殷宗澤和朱俊高教授共同開發的BCF951平面應變有限元計算程序,模擬樁不同深度的土層中樁土相互作用,研究樁周土體初始側向(徑向)應力、樁徑、土體黏聚力、內摩擦角和彈性模量、泊松比變化對樁極限位移的影響.

朱俊高等[10]已對有限元模型尺寸、邊界條件及模型實現過程進行了闡述,因此本文不再贅述.

1.2 樁、土體參數

有限元計算中采用理想彈塑性模型模擬土體的應力應變關系,采用Goodman接觸面單元模擬樁、土之間的錯動.主要參數取值見表1～2.

表1 有限元計算中樁及土體參數

表2 樁土接觸面參數

為研究這些參數對樁極限位移的影響規律,當考察樁徑或土體某一個參數對樁極限位移的影響時,保持其它參數不變,并取表1 中的樁及土體基本參數(第一行參數).對每種參數變化時,土體初始側向應力都變化取值進行計算.實際上,不同的初始側向應力對應不同的土層深度,從而可以將極限位移與深度聯系起來.

2 樁極限位移影響因素分析

圖2給出了不同應力狀態下Xu/D(樁極限位移與樁徑比)和黏聚力c的關系.從圖2可以看出,Xu/D隨著c的增加呈線性增大.

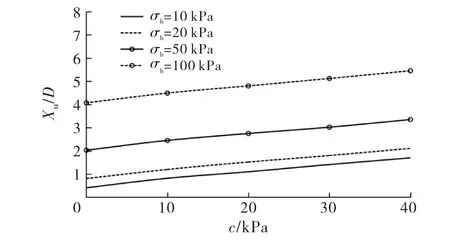
圖2 X u/D 與c 的關系曲線

圖3給出了不同應力狀態下Xu/D和內摩擦角φ的關系.從圖3可以看出,Xu/D隨著φ的增加呈非線性增大.

圖3 X u/D 與φ 的關系曲線

圖4給出了不同應力狀態下Xu/D和彈性模量E的關系.從圖4可以看出,Xu/D隨著E的增加呈非線性減小.

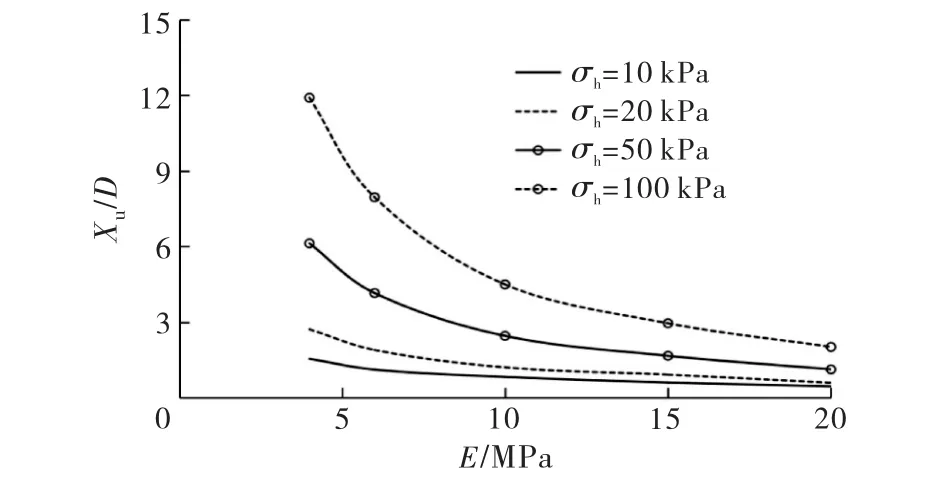
圖4 X u/D 與E 的關系曲線

圖5給出了不同應力狀態下Xu/D和泊松比υ的關系.從圖5可以看出,Xu/D隨著υ的增加呈非線性增大.

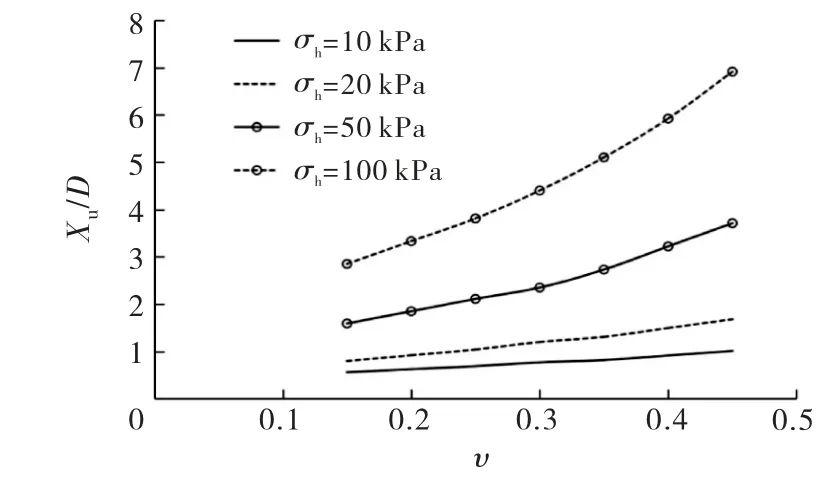
圖5 X u/D 與υ 的關系曲線

圖6給出了不同應力狀態下Xu/D和樁徑D的關系.從圖6可以看出,Xu隨D的增加按比例線性增大.

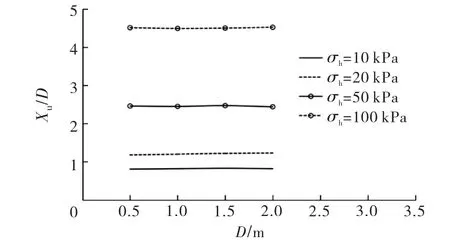
圖6 X u/D 與D 的關系曲線

圖7顯示了各參數變化率與Xu/D變化率的關系.在分析中,取c=20 k Pa、φ=20°、E=10 k Pa、υ=0.3以及D=1.0 m 為基準值,分析各參數相對基準值的增減而引起Xu/D的變化.從圖7可看出,Xu/D隨E的增加而減小,隨參數c、φ、υ的增加而增大,其中φ和E的變化對Xu/D的影響很大,其次υ和c的變化對Xu/D的影響也較大,而樁徑的變化對Xu/D幾乎沒有影響,即Xu隨D的增大按比例線性增大.

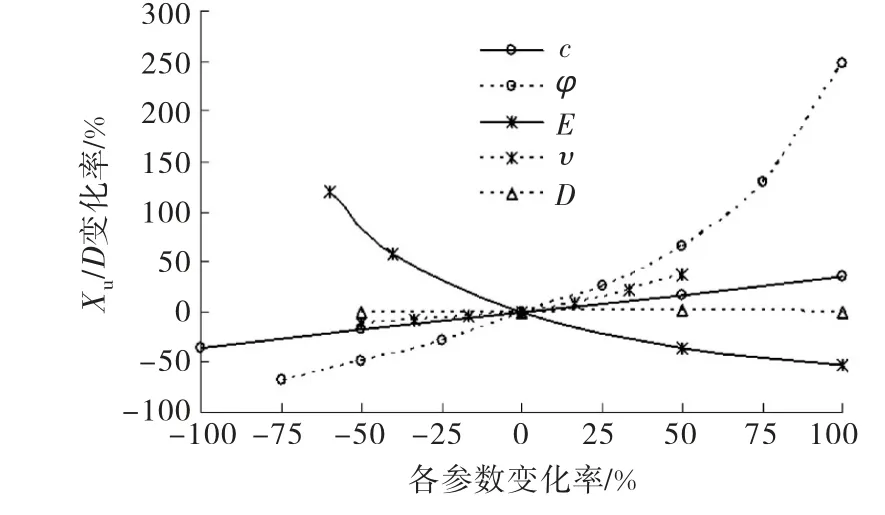
圖7 各參數變化率與X u/D 變化率的關系曲線

圖8給出了取不同彈性模量、泊松比、內摩擦角時Xu/D和初始應力σh的關系.由圖8可知,Xu/D隨著樁周土體初始應力的增加呈線性增大.

圖8 X u/D 本文模型與有限元計算值比較

3 抗滑樁極限位移計算模型

3.1 樁極限位移計算模型

通過采用蒙特卡羅法[11]對有限元計算成果進行擬合分析,本文給出了可以考慮樁徑D、初始應力σh及土體參數c、φ、E、υ等因素的抗滑樁極限位移的計算模型(以下簡稱“本文模型”):

式中:Xu(z)為樁深度z處的極限位移,m;D為樁的直徑,m;σh為樁周土體初始側向應力,k Pa,可按σh=k0γz計算;k0為靜止側壓力系數;γ為土體容重,k N/m3;c為土體黏聚力,k Pa;φ為土體內摩擦角,(°);E為土體彈性模量,MPa;υ為土體泊松比.

另外,為了反映E、υ和φ的非線性影響,本文通過對有限元計算成果的擬合,在式(1)中引入了N E、Nυ和Nφ3個參數,其中

關于泊松比的取值,據文獻[12],較軟黏土可取0.4,較硬黏土可取0.2,一般黏土可取0.3.

3.2 計算模型的精度分析

計算模型中引入了參數N E、Nυ和Nφ分別反映E、υ和φ對抗滑樁極限位移的非線性影響.為驗證參數N E、Nυ和Nφ的擬合精度,本文分別采用有限元法和本文模型計算了不同彈性模量、泊松比和內摩擦角時的Xu/D值,如圖8所示.

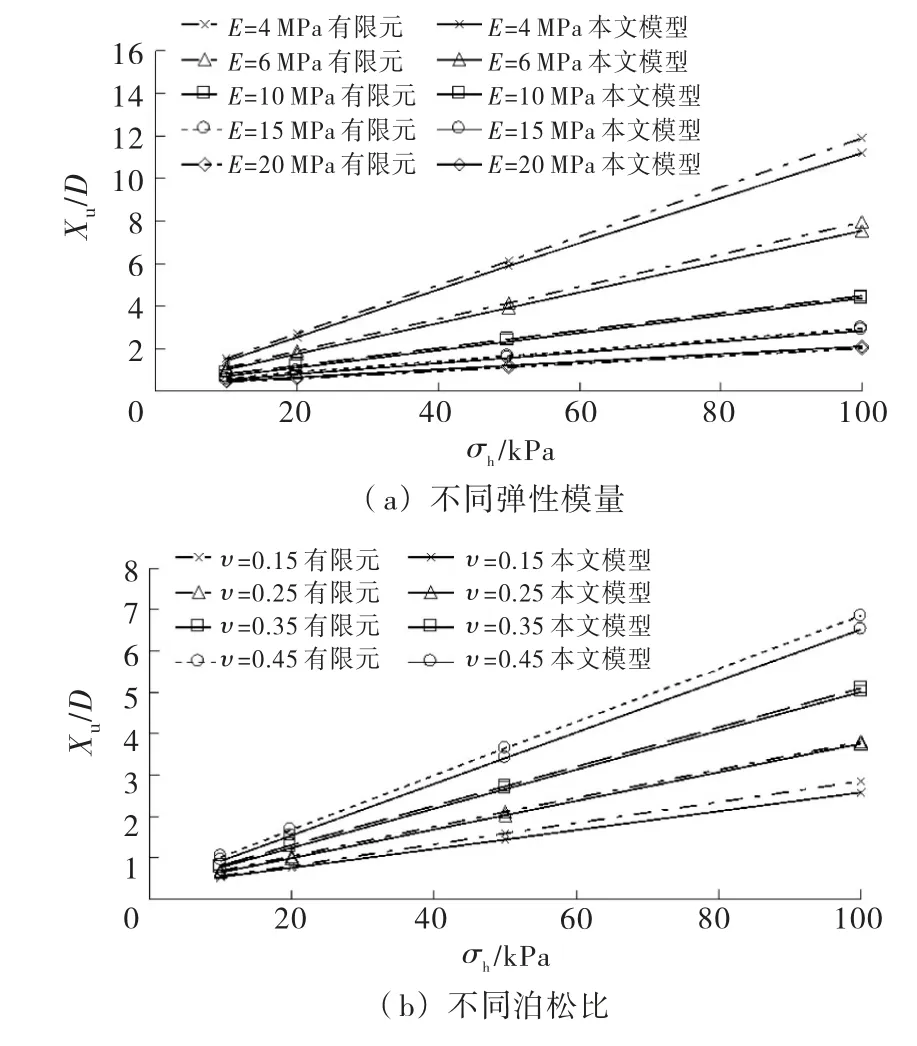
由圖8可知,采用有限元法和本文模型得出的極限位移值很接近,說明參數N E、Nυ和Nφ對E、υ和φ的非線性擬合精度是比較好的.在圖8的計算中,除彈性模量、泊松比和內摩擦角分別變化取值外,其它參數按表1中的樁土體基本參數取值.

4 樁側阻力分布型式研究

4.1 樁極限阻力的分布型式

筆者曾在文獻 [7]給出了抗滑樁極限阻力的計算模型,具體見式(2):

式(2)中,公式第一項“8.1c D”與σh無關,公式第二項“50.8σhNφNυDtanφ”與σh呈正比例增大.所以極限阻力Fu與初始應力σh的關系如圖9 所示,Fu與σh的關系是呈直線變化的.根據σh=k0γz可知,初始側向應力σh與深度z之間呈正比例變化.所以,如果k0γ沿深度z不變化,即k0γ為常數,則極限阻力Fu(z)與深度z的關系也是呈直線變化的;若k0γ沿深度z呈拋物線型式分布,則極限阻力Fu(z)與深度z的關系也是呈拋物線型式分布.即極限阻力Fu(z)沿深度z的分布型式取決于k0γ沿深度z的分布型式.

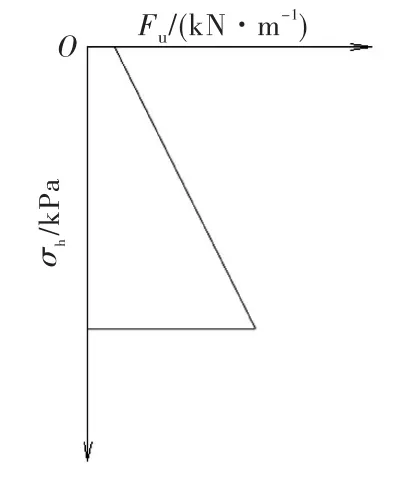
圖9 F u 與σh 的關系

4.2 樁側阻力的分布型式

由上面的分析可以得到樁極限阻力Fu(z)沿深度z的分布型式,又由于實際樁側阻力F(z)的分布型式與極限阻力Fu(z)的分布型式一般不相同,圖10為某一深度z處樁阻力F(z)與樁位移X(z)的關系曲線.

由圖10可知,當樁位移X(z)＜Xu(z)時,樁阻力F(z)可按F(z)=Fu(z)來計算;當X(z)≥Xu(z)時,樁阻力F(z)=Fu(z).

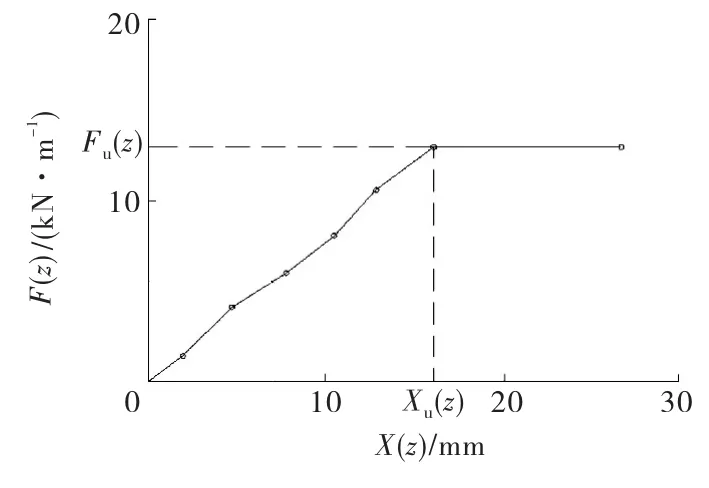
圖10 z 處F(z)與X(z)的關系曲線

5 結 論

本文通過上述分析,可以得出以下結論:

1)提出了抗滑樁極限位移的概念;研究抗滑樁極限位移,對抗滑樁變位安全監測及確定樁側阻力分布型式均具有一定的意義.

2)抗滑樁極限位移Xu隨土體參數φ、υ的增加呈非線性增大、隨E的增加呈非線性減小、隨c及樁徑D的增加呈線性增大.

3)給出了抗滑樁極限位移計算模型,Xu(z)=0.03c D+17.78σhN E NυNφDtanφ.

4)給出了樁樁側阻力分布型式的確定方法.

本文關于抗滑樁極限位移的有關結論,僅是通過分析有限元成果得出的,其合理性尚需進一步驗證.本文抗滑樁極限位移計算模型的土槽模型試驗驗證筆者將另文討論.