海上浮式風機重力安裝式筒形錨承載特性分析

康思偉，欒辰宇，張雨蓉，李颯

（1.中海油融風能源有限公司，上海 200120；2.天津大學建工學院，天津 300072）

0 引言

隨著我國海上風電的迅速發(fā)展，有關海上風電技術的研究越來越受到工程界和學術界的重視[1]。浮式風機是一種安裝在浮動結(jié)構(gòu)上的海上風力發(fā)電裝置。浮式風電場具有以下優(yōu)勢：可以進一步增加海上風力開發(fā)的范圍和深度；可以解決近海用海矛盾突出的問題；對海床擾動小，較少干涉人類活動；為近海與航運通道提供更多空間；可為海上石油和天然氣設施提供綠色電力[2]。浮式風機現(xiàn)有錨型主要有重力錨、打入樁錨、拖曳埋置錨、吸力樁錨、動力貫入錨與平板錨[3]。吸力樁錨、重力錨以及拖曳埋置錨已經(jīng)被應用于海上浮式風電的建設中[4，5]。

吸力錨是一種常用的錨固基礎型式，常用于承受傾斜荷載的條件。Aubeny C P[6]對吸力錨受傾斜荷載作用下的承載力進行了研究，提出了一種計算傾斜荷載條件下吸力錨承載力的簡化上限解。Magued Iskander[7]對吸力錨在粘土和砂土中的特性進行了對比分析，指出在砂土中安裝吸力錨時，容易出現(xiàn)超土塞現(xiàn)象，且吸力安裝有可能導致其承載力的降低。目前，吸力錨更多地被應用于粘性土當中[8，9]。針對浮式風機的受力特征，Laszlo Arany[10]提出了作為浮式風機錨固基礎的吸力錨的設計計算流程，指出了由于浮式風機受力特征與一般海洋結(jié)構(gòu)物不同，設計荷載的準確對于吸力錨的設計至關重要，其在粘土中的設計計算方法可參考海洋工程中吸力錨的設計方法。

拖曳錨也是浮式風機錨固基礎的一種選擇，拖曳錨的精確定位是拖曳錨研究中的關鍵問題。毋曉妮[11]研究了黏土中淺埋拖曳錨的運動性能，并指出在埋深較淺的情況下，埋深比和方位角對土體中的屈服面均有影響。張春會[12]基于增量迭代法提出了預測拖曳錨嵌入運動軌跡和系泊點拉力的模型。但由于拖曳錨不能承受垂直荷載且需要相當長的拖曳距離，從而導致更大的現(xiàn)場調(diào)查成本，并增加了干擾現(xiàn)有系泊線和海底管道的可能性[13，14]。

重力錨的適用范圍廣，施工簡單。重力錨主要用于海底管道的管匯系統(tǒng)，也被稱為防沉板。針對重力錨，Gourvence S[15]提出了考慮H-V-M效應的重力錨破壞包絡面方程。

重力錨也被用于海管鋪設的起始錨，李颯[16]探討了這類重力錨在復合荷載作用下的承載機理。這種重力錨由于其功能所限，重量一般都在十幾到幾十噸的量級。由于重力錨主要靠重力提供承載力，與其他錨固形式相比，其水平承載效率較低[17]。還有一些重量大的重力錨，主要被用于固定近海的海上結(jié)構(gòu)物。

我國海域地質(zhì)條件非常復雜，常常出現(xiàn)砂土或硬粘土地質(zhì)。為此，本文以我國南海某海域粗砂地質(zhì)為背景，考慮到粗砂滲透性較大，無法采用吸力安裝，因此提出了采用重力安裝方式的重力安裝式筒形錨，該錨型可以提供近2 000 t的承載力，可用于粗砂等滲透性較大的風電場地，并利用數(shù)值分析對其貫入過程以及承載特性進行分析。

1 工程背景及錨固基礎型式

南海某海域海底5 m深范圍內(nèi)均為粗砂，粗砂的基本物理力學性質(zhì)見表1，海域的海況條件見表2。

表1 土層物理力學性質(zhì)Table 1 The physical and mechanical properties of soil

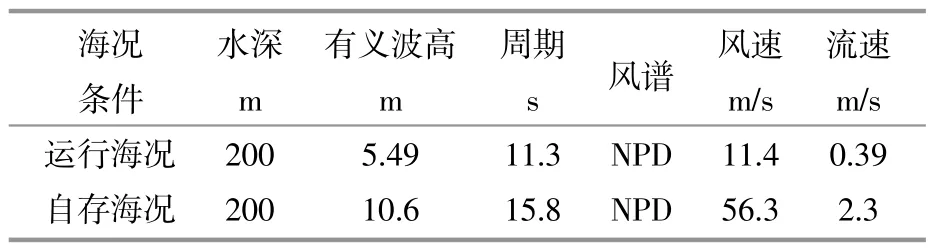
表2 南海某海域環(huán)境參數(shù)Table 2 Environmental parameters of a certain area in the South China Sea

本文采用半潛式浮式風機結(jié)構(gòu)計算錨固基礎的所受荷載，其中，浮式平臺塔架浮筒上的穩(wěn)態(tài)風量的表達式為

式中：Fw為風載荷推力，N；Cw為系數(shù)，一般取0.615 N?s2/m4；Cs為風力形狀系數(shù)；Ch為風力高度系數(shù)；A為暴露在風中的塔架表面的垂直投影面積，m2。

采用NPD陣風譜來表示某處的時變風力，其表達式為

式中：SNPD（f）為NPD風譜的譜密度，m2/s；z為海平面的垂直高度，m；fw為風速頻率；U10為海洋靜水面以上高10 m處的10 min內(nèi)平均風速，m/s。

采用Morison公式計算波浪荷載。

對單位波浪載荷積分得到總的波浪力為

式中：Fw（t）為某時刻浮式平臺所受波浪荷載；ρw為流體的密度，kg/m3；CD為拖曳阻力系數(shù)；Dp為浮式平臺結(jié)構(gòu)的截面尺寸，m；u（z，t）為某時刻垂向分布浮式平臺結(jié)構(gòu)截面的水質(zhì)點速度，m/s；Cm為慣性力系數(shù)；Ap為浮式平臺結(jié)構(gòu)的截面波浪方向的正投影面積，m2；a（z，t）為某時刻垂向分布浮式平臺結(jié)構(gòu)截面的水質(zhì)點加速度，m/s2；B為浮式平臺水下部分吃水長度，m；η為海平面標高，m；S為海域水深，m；z為海平面的垂直高度，z=0即為靜水面，m。

海流荷載的計算式為

式中：FC為作用于浮式平臺的海流力；Ad為浮式平臺靜水面以下部分迎流方向的投影面積，m2；vc為海流的流速，m/s。

根據(jù)環(huán)境載荷以及上述計算式，得到浮式風機錨固基礎在運行海況條件下的水平荷載為11.2 MN，在自存工況條件下的水平荷載為14.4 MN。如果考慮安全系數(shù)為1.5，則其錨固基礎需要提供約22 MN（2 200 t）的水平承載力。由于粗砂的密封性差，采用吸力錨安裝風險較大，因此采用了重力安裝式筒形錨。為了進一步說明重力安裝式筒形錨的承載特性，本文同時對常規(guī)重力錨進行了計算分析。

重力安裝式筒形錨[圖1（a）]的重力塊采用混凝土制成，尺寸為15 m×15 m×6 m。重力塊下的筒形基礎高度為4 m，壁厚0.05 m，重量約94 t，整體重量3 200 t左右。常規(guī)方形重力錨采用混凝土制成[圖1（b）]，尺寸為15 m×15 m×6 m，干重約3 100 t。

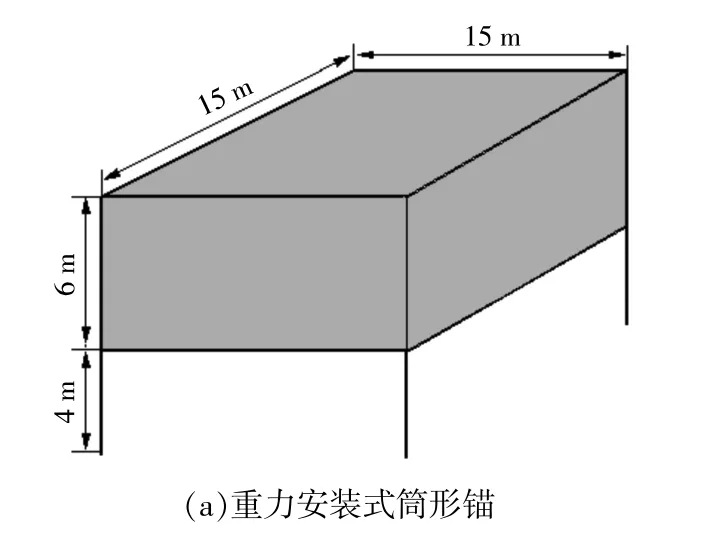
圖1 兩種錨型Fig.1 Two kinds of anchor

2 重力安裝式筒形錨的貫入

重力安裝式筒形錨需要通過筒形基礎的貫入來提高錨固基礎的水平承載力，因此能否貫入至設計深度是這種錨固基礎能否成功使用的關鍵。在巖土工程中的下沉貫入屬于大變形問題。對于大變形問題，目前的有限元模擬方法主要有任意拉格朗日-歐拉法（ALE）[18]、網(wǎng)格重劃分和插值技術法（RITSS）[19]，耦合歐拉-拉格朗日法（CEL）[20]。其中RITSS實質(zhì)上還是ALE法，它主要是將全自動網(wǎng)格重劃分和現(xiàn)行插值技術與小變形計算相結(jié)合，以此避免大變形所造成的網(wǎng)格畸變。此外，還有學者采用了流體動力學法（CFD）[21]以及離散元法（DEM）[22]進行貫入模擬。

由于CEL方法結(jié)合了拉格朗日法與歐拉法的優(yōu)點，利用了歐拉法中材料可以在網(wǎng)格里自由流動而網(wǎng)格保持固定位置這一特征建立模型，該模型可以有效解決大變形問題。因此，本文計算采用了CEL方法，通過有限元程序ABAQUS/Explicit模塊實現(xiàn)。其中錨采用拉格朗日體，地基采用歐拉體。考慮到貫入工況的對稱性，計算模型（圖2）取實際模型的1/4。

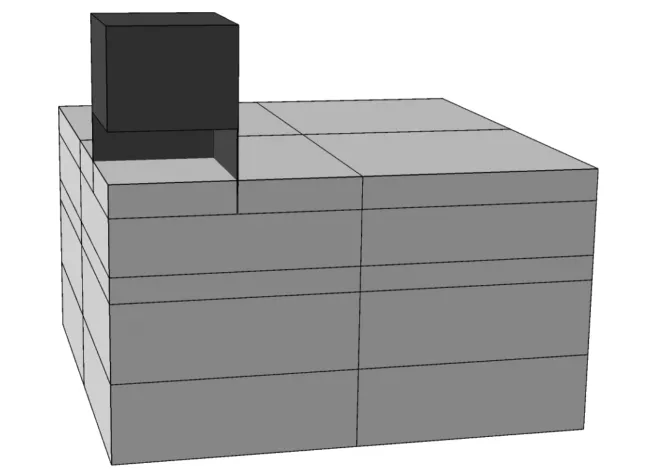
圖2 貫入的計算模型Fig.2 Penetration model

計算中將錨視為剛體，其單元類型為8節(jié)點三維體單元，單元默認劃分尺寸為0.2 m。地基的計算深度為15 m，長度和寬度均為50 m。為了允許錨貫入過程中土體向上隆起，建立模型時在地基表面向上取2 m為計算模型的一部分，該部分區(qū)域初始材料設置為空。在貫入過程中，地基土會發(fā)生大變形，因此土體采用8節(jié)點三維歐拉體單元，本構(gòu)關系采用M-C模型，模型參數(shù)取值見表1。

錨的總重為其實際水下重量，通過施加重力加速度的方法實現(xiàn)。地基底部3個方向上的速度設為0，對稱面上法向速度為0，其他3個側(cè)面3個方向速度為0。錨的對稱面法向位移固定，其他位置可以自由移動。錨和地基之間設置接觸面單元。法向接觸為硬接觸，由于地基貫入深度范圍內(nèi)的土體全部為砂土，切向摩擦系數(shù)取為0.4。

計算得到錨的貫入速度變化曲線如圖3所示。

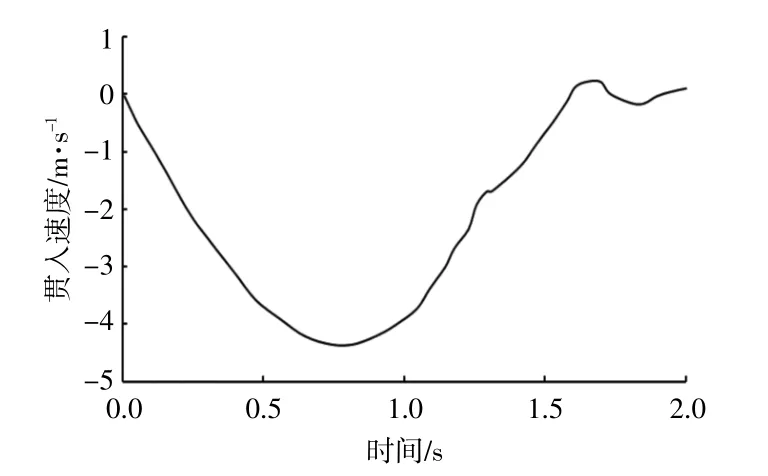
圖3 錨的貫入速度隨時間的變化關系Fig.3 The relationship between penetration velocity and time

計算得到錨的貫入深度隨時間的變化過程如圖4所示。由圖4可知，錨的最終貫入深度為4.2 m，說明重力塊可以保證筒形基礎貫入至設計深度4 m。

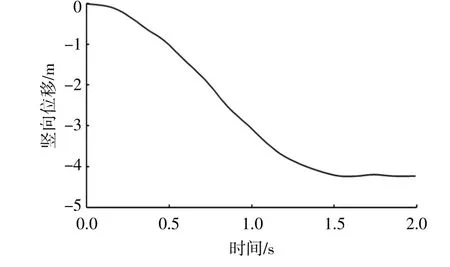
圖4 錨的貫入深度隨時間的變化關系Fig.4 The relationship between penetration depth and time

根據(jù)錨的貫入速度可以將錨的貫入過程分為兩個階段。第一階段是貫入速度增加的過程，該過程持續(xù)到0.88 s時速度達到最大值，此時對應的貫入深度約為2.2 m。表明在此深度范圍內(nèi)，錨受到的貫入阻力小于錨的自重，錨為加速運動。第二階段錨的貫入速度開始降低，直至降低為0，貫入過程停止。這表明第二階段錨受到的阻力大于錨的重力，錨開始做減速運動，直至貫入停止。

3 不同錨固基礎的承載特性

在保證重力安裝式筒形錨可以貫入至設計深度后，進一步分析錨固基礎的承載特性。錨固基礎的承載力可采用小變形方法進行計算。本文采用拉格朗日有限元法，利用ABAQUS進行計算。計算針對重力安裝式筒形錨和常規(guī)重力錨展開。重新建立有限元模型，由于采用拉格朗日有限元法計算，錨體和土體的單元類型均為8節(jié)點三維體單元。考慮到承載條件下的受力情況的對稱性，為節(jié)省計算時間，采用了半模進行分析。地基的計算深度為15 m，長度為100 m，寬度為50 m，以上模型尺寸可以消除邊界的影響。地基土采用M-C模型，為反映筒形基礎和土的相互作用，在土-筒表面采用摩爾庫侖罰函數(shù)的形式。采用位移加載法施加水平荷載，系泊點（荷載作用點）在重力錨上底面中心位置。

圖5（a）為常規(guī)重力錨土體中塑性區(qū)的分布。由圖中可以看到，在水平力的作用下，常規(guī)重力錨塑性區(qū)主要出現(xiàn)在重力錨底部的有限范圍，依靠重力錨底部與土體的摩擦提供抗滑力。圖5（b）為重力安裝式筒形錨的土體中塑性區(qū)的分布。為清楚起見，給出三維圖。從地基破壞時的塑性變形圖可以看出，地基的破壞形式為典型的淺層破壞，筒體范圍內(nèi)的土體已全部被破壞。

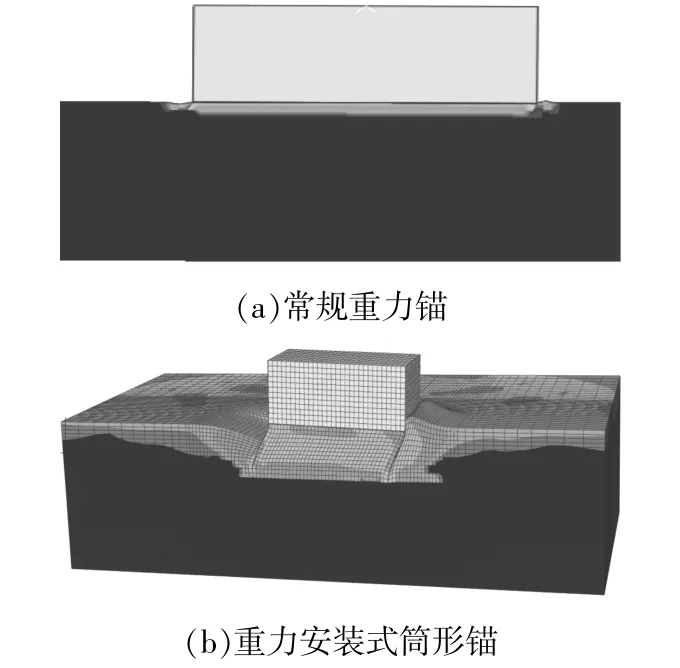
圖5 水平荷載下地基破壞時的塑性區(qū)Fig.5 The plastic zone under horizontal loading

除此之外，本文還對兩種不同類型的基礎形式進行了豎向抗拔承載力的計算。圖6為常規(guī)重力錨和重力安裝式筒形錨在承受上拔力時土體中的塑性區(qū)分布。

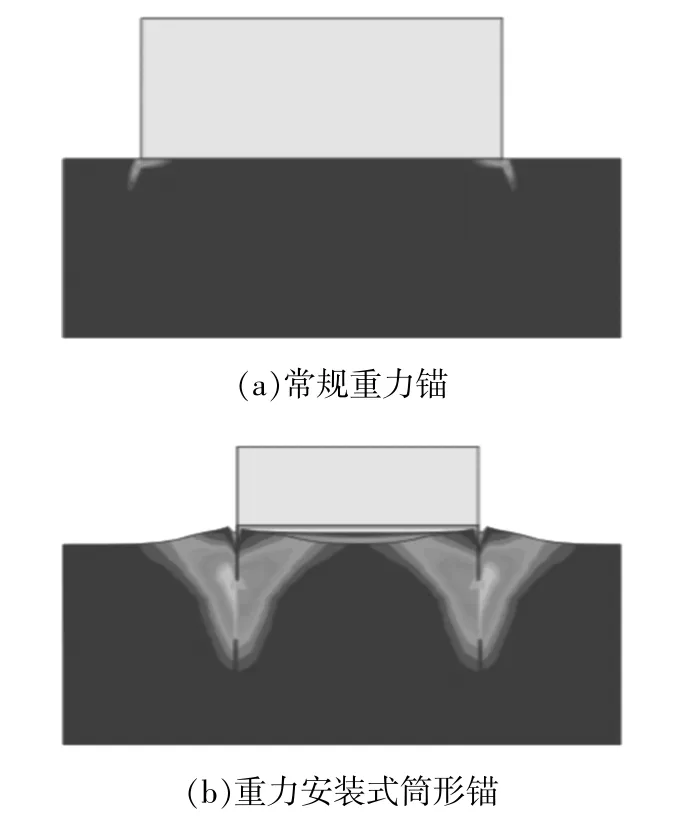
圖6 上拔荷載下地基破壞時的塑性變形Fig.6 The plastic zone under pullout loading

由圖6可知：由于常規(guī)重力錨僅與土層表面相接觸，土體的塑性應變范圍很小，僅有與土體接觸面的四周的少量土體產(chǎn)生了塑性區(qū)，這說明常規(guī)重力錨主要依靠自重抵抗上拔力；當重力安裝式筒形錨受到上拔力時，筒形周圍斜向上產(chǎn)生楔形體塑性區(qū)，且由于土體為砂土，筒形基礎的頂面與土體產(chǎn)生了分離，主要為筒形側(cè)壁的摩擦力以及自身的重量抵抗上拔力，這種破壞模式一般稱為不密封破壞模式。

前文計算分析了錨固基礎在分別承受水平荷載和上拔荷載時的破壞模式。當錨固基礎承受傾斜向上的荷載時，即同時受水平（H）和上拔（V）荷載時，需要考慮采用H-V耦合效應對承載力的影響[15]。考慮H-V耦合效應時，有限元的計算模型不變，但加荷方式發(fā)生變化。本文采用常用的Swipe加載方法進行計算。首先，沿X方向采用位移控制法施加荷載，直至達到極限承載力；然后，保持X方向的位移不變，沿Y方向施加位移荷載，直至達到極限承載力。得到的加載軌跡可作為基礎的破壞包絡線[23]。采用上述方法得到的兩種基礎的H-V破壞包絡線如圖7所示。

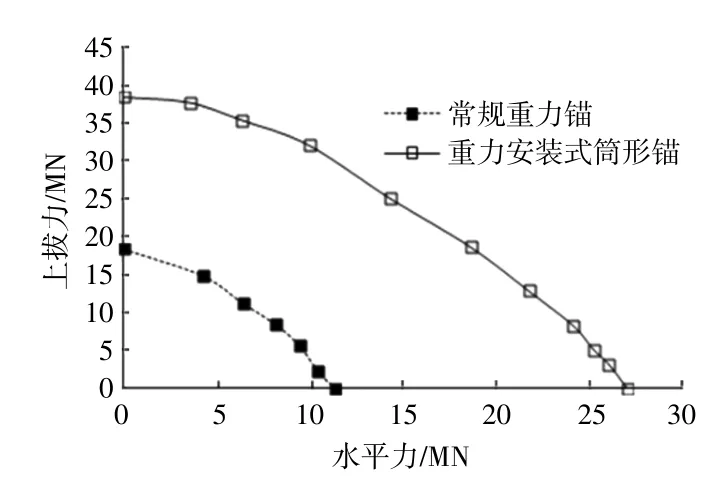
圖7 兩種錨型的H-V破壞包絡線Fig.7 The failure envelope of two kinds of anchor

由圖7可知：由于重力安裝式筒形錨可以調(diào)動更大范圍內(nèi)地基土的承載力，其水平向承載力超過2 500 t，滿足浮式風機的承載要求；常規(guī)重力錨的水平承載力為1 100 t左右，重力安裝式筒形錨的水平承載力為常規(guī)重力錨的2倍以上；由于上部重力塊的重量較大，重力安裝式筒形錨H-V破壞包絡面的形狀更加接近于圓形而不是常見的橢圓形。

4 結(jié)論

本文針對高滲透性砂土提出了一種重力安裝式筒形錨，采用CEL法模擬了重力安裝式筒形錨的貫入。利用拉格朗日法分別計算了重力安裝式筒形錨和常規(guī)重力錨的水平和抗拔承載力，同時采用Swipe加荷方式得到了兩種類型錨固基礎的H-V破壞包絡面。

①采用重力塊將筒形基礎貫入至土體一定的深度是可行的。重力安裝式筒形錨可以作為土體滲透性較大，吸力錨安裝存在困難條件下的一種選擇。

②由于存在一定的入泥深度，重力安裝式筒形錨在承載過程中將形成更大范圍的塑性區(qū)，因此對具有幾乎相同重量的重力安裝式筒形錨和常規(guī)重力錨，重力安裝式筒形錨的水平承載力可以達到常規(guī)重力錨的2倍。

③對于砂土中的筒形基礎，其上撥破壞為不密封模式。在這種破壞模式下，重力安裝式筒形錨在復合加載模式下的H-V破壞包絡面的形狀更加接近于圓形。

④重力安裝式筒形錨可以作為粗砂質(zhì)海底條件下浮式風機錨固基礎的一種選擇。