修正的晶體相場方程的無條件能量穩定數值格式
梁譯泓 賈宏恩,2,*
(1.太原理工大學數學學院,晉中,030600?2.智能優化計算與區塊鏈技術山西省重點實驗室,晉中,030619)
1 引言
晶體相場方程(PFC)是由Elder 等引入相場變量模擬材料在原子空間尺度和擴散時間尺度上的微觀結構時提出的[1,2].這種方程用途廣泛,可以模擬晶粒增長、外延增長、裂紋擴展等行為.PFC 方程經Stefanovic 等加入彈性相互作用后發展為修正的晶體相場方程(MPFC)[3,4].該方程可以自洽地模擬大尺度上的快速彈性松弛.但文獻[5]指出,MPFC 方程的原始自由能在某些時間區間上會隨時間增長,因此需要引入一個偽能量并且證明它是耗散的.與PFC 方程相比,MPFC 方程引入了高階時間導數,這給數值格式的構造帶來了困難.對此,文獻[6,7]提出了非線性且能量穩定的數值格式,文獻[8]對MPFC 方程給出了LDG 方法,文獻[9]提出了一個全離散的有限元格式,文獻[10] 通過IEQ 方法提出了3 個線性的、無條件能量穩定的數值格式,文獻[11,12]通過SAV 方法提出了線性的、無條件能量穩定的格式.
為了構造MPFC 方程的二階線性格式,本文基于文獻[13]中的拉格朗日乘子法,對空間六階的非線性方程進行降階處理.本文結構如下:第二節介紹MPFC 方程并對其能量進行修正?第三節應用拉格朗日乘子法構建一個二階的數值格式,然后證明這個格式是質量守恒、唯一可解及無條件能量穩定的?第四節對這個二階格式進行嚴格的誤差估計?最后一節通過數值算例對理論分析進行驗證.
2 MPFC 模型
Swift-Hohenberg 型自由能泛函為[1]
其中??Rd(d=2,3),變量?(x,t)表示密度場,常數?∈(0,1).修正的相場晶體模型可以寫成一個偽梯度流的形式:
其中常數α>0,β >0,遷移率常數M >0,化學勢μ定義為
其中變量滿足周期邊界條件.方程(2.2)的初始條件為?(x,0)=?0,?t(x,0)=ψ0.
對式(2.2)兩端積分得到常微分方程
引入一個新變量ψ(x,t):=?t(x,t),則.用算子(-?)-1作用于式(2.2)兩邊后代入式(2.3),再與?t作內積,可得MPFC 方程滿足下述能量耗散律:
3 二階數值格式
通過引入兩個輔助變量u(x,t)=?2,w=??,式(2.1)可以改寫為
偽能量式(2.4)可以改寫為
式(2.2),(2.3)的等價形式為
因為式(3.5)是一個常微分方程,故u不需要邊界條件,其余變量取周期邊界條件,初始條件為
用(-?)-1作用于式(3.2)兩邊,再與?t作內積,并將式(3.6)代入得
然后將式(3.5)兩邊與?t,分別做內積得
再將式(3.6)兩邊與-w做內積得
最后,綜合式(3.7)–(3.10),得
注3.1 對式(3.5)關于時間求積分可得u=?2,把它和式(3.6)代入式(3.2)與(3.3)可得到式(2.2)和(2.3),因此,(2.2)與(3.2)–(3.6)這兩個系統是等價的.(3.2)–(3.6)關于修正的能量式(3.1)是無條件穩定的.本文將對系統(3.2)–(3.6)構造數值格式,使其滿足新能量律(3.11).
以下,用δt表示時間步長,tn=nδt(0≤n≤N=),?n表示?(tn)的數值近似,C泛指某個正常數,它與δt和n無關,在不同情況下可以取不同的值.
下面對系統(3.2)–(3.6)構造二階格式.
對于1≤n≤N-1,若已知(?n,ψn,un,wn) 和?n-1,則通過下述方式求解(?n+1,ψn+1,un+1,wn+1):
其中初始條件為?0=?0,ψ0=0,u0=(?0)2.
注3.2 式(3.12)–(3.16)和式(3.17)–(3.21)都是通過引入拉格朗日乘子u=?2得到的,它可以看作IEQ 方法[2]的一個特例.與文獻[2]不同的是本文顯式處理2??,得到一個強制的雙線性形式a(·,·).
對式(3.12)–(3.16)進行等價變形得到
其中,
由式(3.22)可得到?n+1,μn+1,wn+1,然后通過式(3.14)和式(3.15)可得到un+1,ψn+1.這樣,引入的輔助變量u和ψ沒有增加額外的計算成本.
由于對于具有周期邊界條件的函數f和g都有
且(P(f),f)=0 當且僅當f≡0 時成立,故線性算子P(?)是對稱正定的.
對式(3.12)和(3.17)兩邊關于x積分得
對式(3.14)與(3.19)兩邊關于x積分得到
這說明系統滿足質量守恒性.
下面討論系統(3.22)(或其等價系統(3.12)–(3.16))的適定性.
定理3.1 線性系統(3.22)存在唯一解.
用(-?)-1算子作用于式(3.23)兩邊,然后將式(3.24),(3.25)代入,可得
令V=,則式(3.26)的變分問題為:求?∈V,使得
其中,
由(?(-?)-1?,?(-?)-1?)≤∥(-?)-1?∥·∥?∥≤∥?(-?)-1?∥·∥?∥及Poincaré 不等式可得∥?(-?)-1?∥≤C∥?∥.因此,a(?,v)=γ((-?)-1?,v)+(P(?),v)+≤C∥?∥2∥v∥2,即a(·,·)是連續的.
由Lax-Milgram 定理知,變分問題(3.27)的解?∈V存在且唯一,因而等價系統(3.22)的解存在且唯一.
類似地可證明初始格式(3.17)–(3.21)的解存在且唯一.定理證畢.
定理3.2 格式(3.12)–(3.16)是無條件能量穩定的,即
其中,
證明用算子(-?)-1作用于式(3.12)兩邊,然后兩邊與?n+1-?n作內積,再結合式(3.14)可得
用?n+1-?n與式(3.13)兩邊作內積得
再將式(3.16)與wn=??n相減,然后兩邊與wn+1+wn作內積得
最后,結合式(3.29)–(3.32)可得
定理證畢.
定理3.3 格式(3.17)–(3.21)是無條件能量穩定的,即
其中,
證明用(-?)-1算子作用于式(3.17)兩邊,然后與(?n+1-?n)作內積,再結合式(3.19)可得
將(?1-?0)與式(3.18)兩邊作內積,得
將式(3.21)與式w0=??0相減,然后兩邊與wn+1做內積,得
最后,結合式(3.35)–(3.38)可得
定理證畢.
4 誤差估計
本節對半離散格式(3.12)–(3.16)進行誤差分析.為簡單起見,用f?g表示f≤Cg.根據離散的能量耗散律(3.28)和(3.34),對數值解?n有如下的H2估計.
定理4.1 假設初始條件足夠正則,且≤C,則||?n||2≤C,其中0≤n≤N.
證明由式(3.34)得≤C.由式(3.39)得≤C.因此,
由式(3.33)得
故
所以,
又因為
所以,
由式(3.32)和式(3.38)知
進一步,有
定理得證.
設(3.2)–(3.6)的精確解(?,ψ,u,w)滿足下列正則性條件:
定義誤差函數:
定理4.2 設(3.2)–(3.6)的精確解滿足正則性條件(4.3).則有
證明將(3.2)–(3.6)改寫為
其中,
它們滿足
由式(4.5)與式(3.20)–(3.22),可得
用算子(-?)-1作用于式(4.6)兩邊,然后與作內積,可得
結合式(4.11)–(4.13)得
上式右端各項的估計如下:
利用這些估計可得
定理證畢.
接下來對二階格式(3.12)–(3.16)進行誤差估計.
將式(3.2)–(3.6)改寫為
其中,
對于截斷誤差式(4.15),有下述定理,其證明略.
定理4.3 在正則性條件式(4.3)下,截斷誤差式(4.15)滿足
由式(4.14)及式(3.12)–(3.16),可得下列誤差方程:
定理4.4 設式(3.2)–(3.6)的精確解(?,ψ,u,w)滿足正則性條件(4.3).則存在某個常數C1使得
證明用算子(-?)-1作用于式(4.17)兩邊,然后與作內積得
下面分析式(4.23)右端各項.
結合式(4.22)–(4.28)得:
下面對式(4.29)的右端各項進行估計.
類似可得:
綜上可得:
對式(4.30)兩邊令n取值1 到m,然后求和(1≤m≤N-1),可得
再由式(4.16)得
再由Gronwall 不等式知,存在某個常數C1,使得
定理證畢.
定理4.5 設(3.2)–(3.6)的精確解滿足正則性條件式(4.3).則
即離散能量式(3.29)是對偽能量式(2.4)的二階近似.
證明根據定理4.4 及三角不等式可得:
進一步,我們有
5 數值實驗
本節的數值實驗都在二維空間中進行,變量均使用周期邊界條件,并且選擇P1有限元空間.例5.1 計算數值格式(3.15)–(3.19)的時間精度,例5.2 模擬相變過程.
例5.1 方程參數設為α=1,β=0.9,M=1,?=0.025,總時間T=1.0,積分區域?=[0,1]2,相變量的精確解為
為了與方程(2.2)保持一致,需要在方程(2.2)的右端增加一個外力項f(x,y,t),即
這里需要將?(x,y,t)的精確值代入f(x,y,t)的表達式中進行計算.
變量?,u的L2誤差表達式分別為
變量?,u關于時間的收斂階的表達式分別為
實驗結果如表1 所示.從表中可以看到隨著時間步長減小,誤差值越來越小,趨于0,收斂階o(?)與o(u)逐漸趨于2.由此說明本文所構造的差分格式在時間上是二階收斂的,與文中理論分析的結論一致.
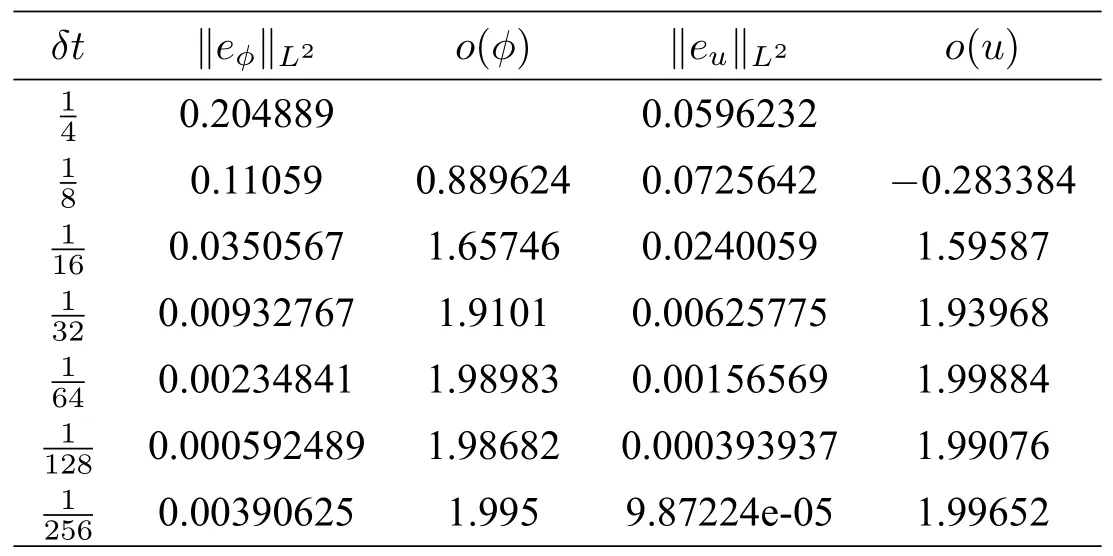
表1 二階格式(3.15)–(3.19)的實驗結果
例5.2 將積分區域?=(0,6π)×(0,6π)分成50×50 個正方形,每個正方形沿左下角(右上角) 對角線劃分,得到一致三角剖分.方程參數設為α=0.1,β=1,M=1,?=2,時間步長δt=0.25,初始條件為
圖1 到圖4 展示了液滴從條形分布到三角形分布的大致變化過程,實驗進行到t=1250 時液滴的三角形分布達到穩定.

圖1 t=5
圖2 t=26.25

圖3 t=30

圖4 t=1250

