一個求解特殊加權線性互補問題的預估校正光滑牛頓法
賀曉瑞 湯京永
(信陽師范大學數學與統計學院,信陽,464000)
1 引言
2012 年,國際著名優化專家Potra 教授在文獻[1]中提出了加權線性互補問題的數學模型:
其中P∈R(n+m)×n,Q∈R(n+m)×n,R∈R(n+m)×m為給定矩陣,a∈Rn+m為給定向量,w≥0 為權重向量,xs表示向量x和s對應分量相乘組成的向量,即xs:=(x1s1,···,xnsn)T.如果加權線性互補問題(1.1)滿足:對任意的(?x,?s,?y)∈Rn×Rn×Rm,當P?x+Q?s+R?y=0 時,總有〈?x,?s〉≥0,則稱其是單調的.
經濟、管理等領域中的許多均衡問題都可以轉化成加權線性互補問題進行求解.雖然有些均衡問題可以轉化成互補問題,比如著名的Fisher 均衡問題,但將其轉化成加權線性互補問題可以更有效地進行求解[1].
許多學者對加權線性互補問題展開了深入研究.Potra 在文獻[1]中給出了兩個求解單調加權線性互補問題的內點算法,分析了算法的多項式迭代復雜性?在文獻[2]中給出了一個求解充分加權線性互補問題的預估校正內點算法,證明了算法的迭代復雜性與求解充分線性互補問題內點算法的最好結果相同.Zhang[3]和Tang[4]分別研究了求解單調加權線性互補問題的光滑牛頓法,分析了這些算法的全局和局部收斂性質.Asadi 等[5]給出了第一個求解單調加權線性互補問題全牛頓步內點算法,證明了算法具有目前最好的迭代復雜性.最近,Tang 和Zhou[6]給出了一個求解非單調加權線性互補問題的阻尼高斯牛頓法,在局部誤差界條件下證明了算法具有局部二次收斂性質.
本文考慮一種特殊的加權線性互補問題:
其中M∈Rn×n為給定矩陣,q∈Rn為給定向量.因為x≥0,s≥0,xs=0 當且僅當x≥0,s≥0,xT s=0,所以如果權重向量w為零向量,那么互補問題(1.2)即為如下標準的線性互補問題:
光滑牛頓法是求解加權線性互補問題(1.1)和線性互補問題(1.3)的一種重要方法([3,4,7,8]),其基本思想是利用光滑函數將優化問題轉化成一個光滑方程組,然后利用牛頓法求解該方程組.
受文獻[3,4,7,8]的啟發,本文利用一個帶有權重的光滑函數將加權線性互補問題(1.2)轉化成一個光滑方程組,然后用一個預估校正光滑牛頓法去求解.在適當條件下,我們將證明給出的算法具有全局和局部二次收斂性質.特別地,在解集非空的條件下,我們將證明價值函數點列收斂到零.最后,我們將用數值試驗驗證我們的算法的有效性.
2 問題(1.2)的等價轉化
考慮如下光滑函數:
其中c≥0 是一個固定常數.
接下來,我們利用光滑函數(2.1)將特殊加權互補問題(1.2)等價轉化成一個非線性方程組H(z)=0.
引理2.1?c在任意點(ε,a,b)∈R++×R×R 處連續可微且
引理2.2 對任意的(ε,a,b)∈R+×R×R,有
證明如果?c(ε,a,b)=0,則由(2.1)可得
上式兩邊同時平方,可得ab=c+ε,從而
如果a≥0,b≥0,ab=c+ε,則由(2.1)可得?c(ε,a,b)=a+b-=0.證畢.
令z:=(ε,x,s),其中ε為光滑函數中的光滑參數,x,s為加權線性互補問題的變量.利用(2.1)給出的函數?,我們定義
其中
由引理2.2 可知H(z)=0 當且僅當ε=0 并且(x,s)是特殊加權線性互補問題(1.2)的解.
引理2.3 以下結論成立:
(i)H(z)在任意點z∈R++×Rn×Rn處連續可微,其雅可比矩陣為
這里I表示n×n單位矩陣,而
其中vec{αi}表示向量α=(α1,···,αn)T,diag{αi}表示第i個對角元素為αi的對角矩陣.
(ii)如果M半正定,那么H′(z)在任意的點z∈R++×Rn×Rn處非奇異.
證明由引理2.1 可知結論(i)成立.類似于文獻[3]中的引理1,我們可證明結論(ii).證畢.
3 算法的構造
下面我們給出求解問題(1.2)的算法.
算法3.1選擇參數σ,δ∈(0,1)和初始點z0:=(ε0,x0,s0)∈R++×Rn×Rn?選取γ∈(0,1)使得γ <ε0且γ+σ <1?選取θ >0 和序列 {θk}使得≤θ <∞.令k:=0.
步驟1 如果∥H(zk)∥=0,則停止迭代.
步驟2(預估步) 如果∥H(zk)∥>1,則令:=zk并轉步驟3.否則,通過求解線性系統
令αk:=,其中lk是滿足下式的最小非負整數l,
步驟4 令k:=k+1.轉步驟1.
注3.1 算法3.1 的框架由Huang,Han 和Chen[9]提出,用于求解線性互補問題(1.3).與文獻[9]中算法的不同之處是,在算法3.1 的校正步中,我們采用非單調線搜索技術來生成步長,這使得我們的算法具有更好的計算效果.
定理3.1 如果M半正定,那么算法3.1 可以產生一個無窮點列 {zk=(εk,xk,sk)},并且對所有的k≥0 有εk >0.
因此,我們得到如下結論:如果zk∈R++×Rn×Rn,那么算法3.1 可以生成zk+1并且zk+1∈R++×Rn×Rn.因為z0∈R++×Rn×Rn,故由數學歸納法可知定理成立.證畢.
4 收斂性分析
引理4.1 設{zk=(εk,xk,sk)}是由算法3.1 生成的迭代序列,則對所有的k≥0 有:(i)∥H(zk+1)∥≤(1+θk)∥H(zk)∥;(ii)εk≥βk.
證明由(3.5)可知,對所有的k≥0 有∥H(zk+1)∥≤.如果預估步成立,那么∥H(zk)∥≤1 且
否則,
結論(i)得證.
接下來,我們假設εk≥βk對某個k成立,例如,它對k=0 成立.如果預估步成立,那么由(3.1)和(3.2)可得
這里最后一個不等式成立是因為序列{βk}單調遞減.由數學歸納法可知結論(ii)成立.證畢.
定理4.1 假設M是半正定的并且{zk=(εk,xk,sk)}是由算法3.1 生成的迭代序列,那么{zk}的任意聚點z?:=(ε?,x?,s?)是H(z)=0 的一個解.
證明對所有的k≥0,因為∥H(zk+1)∥≤(1+θk)∥H(zk)∥且<∞,所以由文獻[10]中的引理2.2 可得,存在一個常數H?≥0 使得
由(4.1)和(4.2),對所有的k≥0 有
現在我們假設H(z?)0,然后推出一個矛盾.顯然,∥H(z?)∥=H?>0.由算法3.1 的步驟3 可得
由此可得
因為{βk}是單調遞減的,所以存在一個常數β?≥0 使得=β?.因為=H?>0,由(3.4)可得β?>0.結合引理4.1(ii)可知
因此,H(z)在z?處連續可微.在(4.9)中令k(∈K)→∞,可得
另一方面,由(3.3)可知
這里不等式成立是因為ε?≤∥H(z?)∥和β?≤γ∥H(z?)∥.由(4.10) 和(4.11) 可知(1-γ-σ)∥H(z?)∥≤0,再結合γ+σ <1 可得H(z?)=0,從而推出矛盾.證畢.
下面我們證明價值函數點列 {∥H(zk)∥} 收斂到零.
引理4.2 設Φw由(2.3)定義.則對任意的(ε,x,s,t)∈R++×Rn×Rn×Rn,有
這里E:=(1,···,1)T.
證明由(2.1)可知對任意的(ε,a,b,?)∈R++×R3,有
從而由引理2.2 可得
利用上述結論,由(2.3)我們可以得到
證畢.
引理4.3 假設M半正定并且 {zk=(εk,xk,sk)} 是由算法3.1 生成的迭代序列.如果特殊加權線性互補問題(1.2)的解集非空,那么有
證明由(4.7)可得
因為對所有的k≥0,有∥H(zk+1)∥≤(1+θk)∥H(zk)∥,故由文獻[10] 中的引理2.1 可知∥H(zk)∥≤eθ∥H(z0)∥,進而可得
這說明序列{εk}是有界的.因為問題(1.2)的解集非空,所以存在(x?,s?)∈Rn×Rn使得
對任意的k=0,1,···,令
由(2.2),(4.13)和(4.14)可知,對所有的k=0,1,···,有
這說明 {(uk,vk)} 是有界的.現在,我們構造另一個序列:
由(4.17)可知Φw(εk,xk,sk)=2(εkvk-εkxk),再結合引理4.2 可得
由(4.15)可知x?s?=w,故〈x?,s?〉=.因此,
由(4.15),(4.18),(4.19),(4.23)和M半正定,可得
這里
由(4.13)和(4.24),對所有的k≥0,有
因為序列 {(εk,uk,vk)} 是有界的,所以如果∥xk∥→∞,那么是有界的.此時,當k→∞時(4.26) 的左邊趨向于+∞,這與(4.26) 矛盾.因此,序列 {xk} 是有界的.再結合 {(εk,uk)} 的有界性和sk=Mxk+q+εkuk可得 {sk} 是有界的.因此,序列 {zk=(εk,xk,sk)} 有界,從而可知 {zk} 至少有一個聚點z?.由H的連續性和(4.12)可知H(z?)=H?.再結合定理4.1 可得H?=0,即=0,進而由(3.4)可知β?=0,從而推出矛盾.證畢.
因為算法3.1 的局部二次收斂速度取決于預估步,所以由文獻[9]中的定理5.1 可得如下結論.
引理4.4 假設M半正定并且 {zk} 是由算法3.1 產生的迭代序列.令z?為 {zk} 的任意聚點.如果所有的V∈?H(z?)都是非奇異的,則 {zk} 收斂于z?并且∥zk+1-z?∥=O(∥zk-z?∥2).
5 數值結果
在本節中,我們通過數值試驗來檢驗算法的有效性.算法3.1 中的參數設置為δ=0.5,ε0=10-4,γ=10-5,σ=10-5,θk=0.9k.我們使用 ∥H(zk)∥≤10-6作為停止準則.
5.1 求解特殊加權線性互補問題(1.2)
本小節應用算法3.1 求解特殊加權線性互補問題(1.2).令M=UUT/∥UUT∥,其中U=rand(n,n),q=rand(n,1).此外,選擇=rand(n,1),=rand(n,1),并令w:=.我們分別使用以下兩個初始點求解這些測試問題:
SP1x0=s0=(1,···,1)T?
SP2x0=(1,0,···,0)T,s0=Mx0+q.
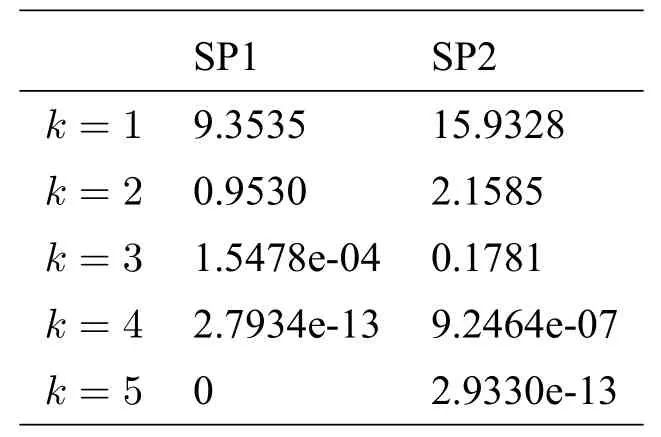
首先,我們生成一個n=1000 的測試問題,然后應用算法3.1 去求解此問題.表1 給出了迭代過程中∥H(zk)∥的值.由表1,我們可以很容易看出算法3.1 具有局部快速收斂性質.
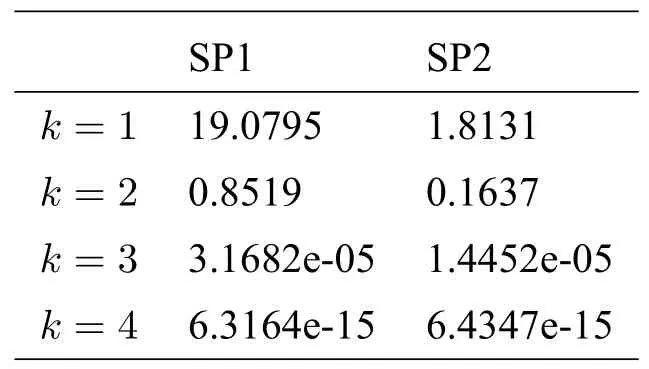
表1 第k 次迭代時∥H(zk)∥的值
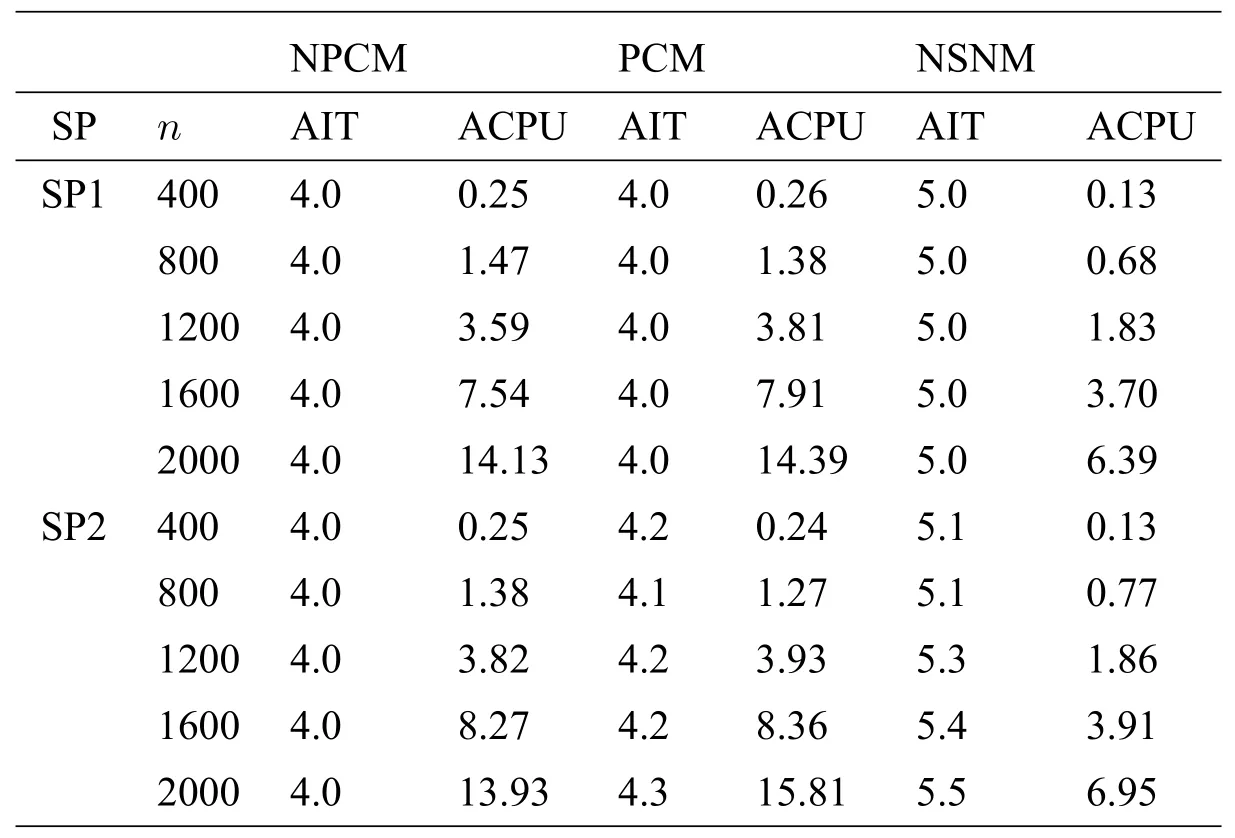
接下來,對于每個測試問題,我們生成10 個算例,然后應用算法3.1 去求解這些算例.數值試驗的結果列于表2,其中SP 表示初始點,AIT 和ACPU分別表示用算法3.1 求解問題所需的迭代次數和CPU 時間的平均值,AHK 表示算法終止時 ∥H(zk)∥的平均值.從表2 可以看出,算法3.1 對于求解特殊加權線性互補問題(1.2)是非常有效的,它只需很少的迭代次數和CPU 時間就可以找到滿足終止條件的解.此外,我們還可以發現,當測試問題的規模變大時,算法3.1 所需的迭代次數變化不大,但所需的CPU 時間增加.
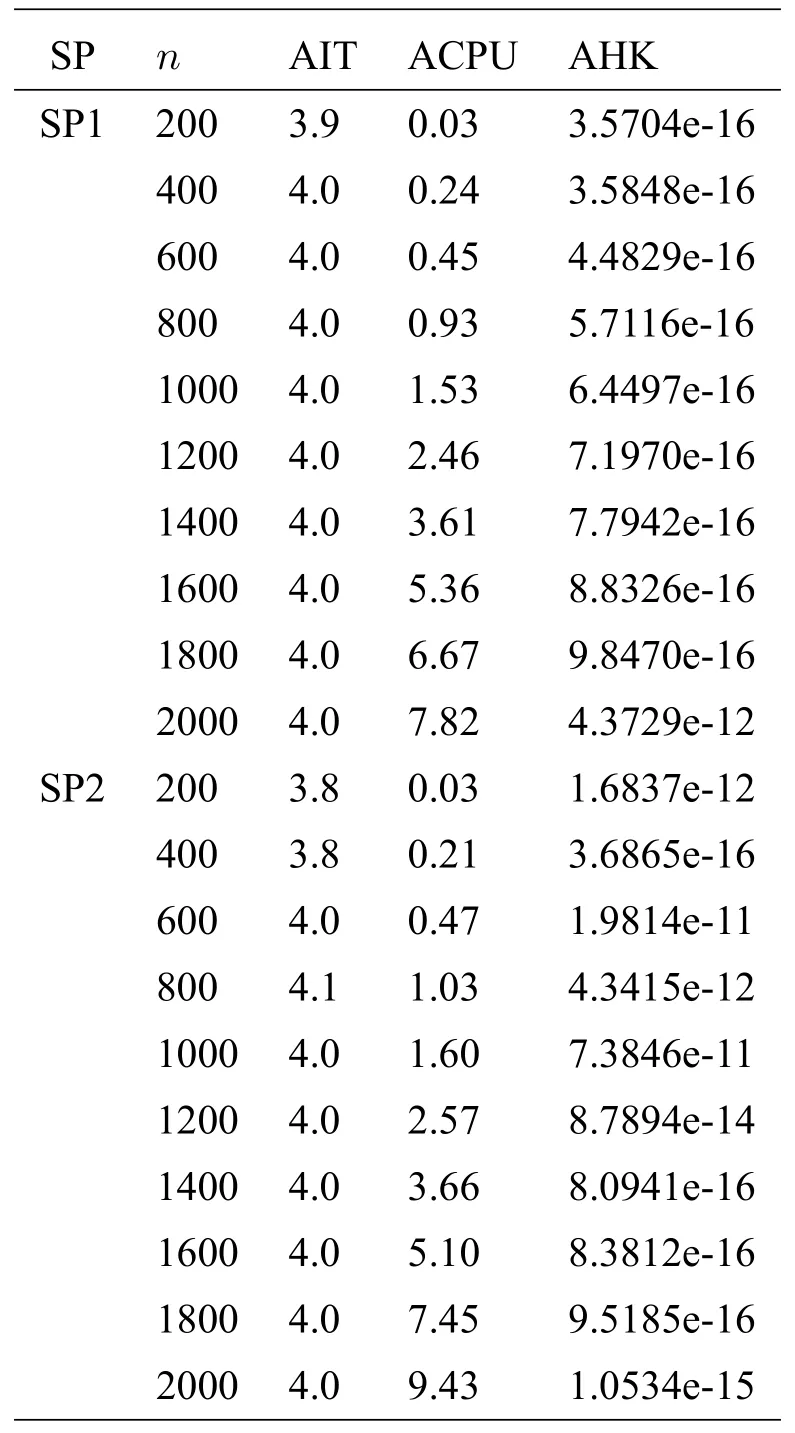
表2 求解問題(1.2)的數值結果
5.2 求解加權線性互補問題(1.1)
本小節應用算法3.1 求解加權線性互補問題(1.1),其中
其中N是一個給定的n×n對稱半正定矩陣,A∈Rm×n是一個m 在試驗中,我們產生一個行滿秩的矩陣A∈Rm×n,然后選擇N=BBT/∥BBT∥,其中B=rand(n,n),=rand(n,1),f=rand(n,1),再定義.對于每個問題,我們分別使用以下兩個初始點進行求解: SP1x0=s0=(1,0,···,0)T,y0=(0,···,0)T? SP2x0=rand(n,1),s0=rand(n,1),y0=rand(m,1). 首先,我們生成一個n=1000,m=500 的測試問題,然后應用算法3.1 去求解.表3 給出了迭代過程中∥H(zk)∥的值,其再一次表明算法3.1 具有局部快速收斂速度. 表3 第k 次迭代時∥H(zk)∥的值 接下來,我們對算法3.1 和文獻[9],[11]給出的算法進行比較. 本文給出的算法3.1,記為NPCM?文獻[9]給出的求解線性互補問題的預估校正光滑牛頓法,記為PCM?文獻[11]給出的求解加權互補問題的非單調光滑牛頓法,記為NSNM. 對于每個n(=2m)的測試問題,我們生成10 個算例,并分別應用上述三種算法求解.數值結果列于表4. 表4 NPCM,PCM和NSNM的數值比較結果 由表4,我們有如下結論: (i)算法3.1 對于求解一般的加權線性互補問題(1.1)也是有效的,它只需很少的迭代次數和CPU 時間就可找到滿足精度要求的解. (ii)算法3.1 比文獻[9]中的預估校正光滑牛頓法更穩定. (iii)與文獻[11]中的算法相比,算法3.1 所需的迭代次數減少而CPU 時間增加.一個合理的解釋是算法3.1 在每次迭代時需要求解兩個線性方程組并進行兩次線搜索,而文獻[11]中的算法在每次迭代時只需求解一個線性方程組并進行一次線搜索.換句話說,與文獻[11]中的算法相比,算法3.1 每一次迭代時∥H(z)∥下降的量更大,但所需的CPU 時間更多.