基于多聯盟非合作博弈納什均衡搜索的集群對抗方法

劉 飛 董希旺,2 化永朝,2 于江龍 任 章

集群系統及集群智能的研究得到了廣泛重視,其在集群編隊、搜索救援、區域偵查等場景[1-3],以及軍事領域具有極大應用潛力.軍用無人集群系統具有分布式、自組織、自主決策的特點,面對常規防御系統可形成非對稱優勢.以無人集群攔截入侵集群是應對其威脅、抵消其優勢的可行方式,由此形成了集群對抗這一研究課題[4].

多聯盟非合作博弈理論可以用來建模與分析無人集群對抗中包含的復雜合作與競爭關系[5].大規模無人集群中可能會基于其載荷或性能特點形成各類異構子群,承擔探測、干擾、攻擊等不同任務.敵我無人集群均可基于上述特點或多樣任務形成多個聯盟.在多聯盟非合作博弈框架下,每個智能體作為實際的決策者驅動其決策變量到達納什均衡點,從而完成集群對抗任務.

多聯盟非合作博弈建模了集群內的合作關系和集群間的非合作關系,其納什均衡搜索算法的設計是實現集群對抗的關鍵.博弈參與者的策略由其動力學及控制輸入驅動[6].對于具有動力學系統的多智能體系統的納什均衡搜索算法設計,可利用時間尺度分離的方式依次進行靜態納什均衡的搜索和定點跟蹤控制[7-8].另一種方法是直接設計分布式反饋控制器[9-10].針對部分信息未知的問題,通?；谝恢滦詤f議進行分布式狀態估計[11-13].

無人集群的對抗中存在著大量的約束條件,主要來自資源或任務約束[14].含有約束的博弈問題的均衡被稱為廣義納什均衡（generalized Nash equilibrium,GNE）.文獻[15-17]提出了分布式的算子分割算法以定步長求解GNE,同時保證了算法收斂性.文獻[18]研究了多聯盟非合作博弈中GNE 的求解問題,考慮了代價函數和約束函數不光滑的情況.另一方面,集群對抗是一個高動態過程,無人集群的任務是時變的,因此,這種情況下多聯盟非合作博弈的納什均衡是一個軌跡,而不是一個靜態策略[19],這對納什均衡搜索算法的設計帶來了更大困難.

本文主要研究基于多聯盟非合作博弈的無人集群對抗的建模方法,提出多聯盟非合作博弈時變納什均衡的搜索策略,主要貢獻總結如下：

1）考慮多聯盟之間存在的耦合約束和局部約束,設計了一種障礙函數處理智能體的局部約束,可用于保證集群對抗的安全性.

2）將障礙函數引入博弈代價函數并轉化為新的多聯盟非合作博弈問題,證明了其廣義納什均衡是原問題的epsilon 廣義納什均衡.

3）基于障礙函數和原對偶方法設計了時變廣義納什均衡搜索算法.分析了該算法在集群對抗中分布式時變編隊隊形設計的應用.

1 問題的提出

1.1 多聯盟非合作博弈模型

考慮集群博弈對抗場景下包含N 個聯盟的多聯盟非合作博弈廣義納什均衡搜索問題.

1.2 廣義納什均衡搜索

給出上述博弈問題的廣義納什均衡的定義.

對于所有的i∈P,j∈Pi成立,其中,.此外,如果存在集合Sij使得,對于任意的i∈P,j∈Pi和xij成立,那么是多聯盟非合作博弈的納什均衡.根據廣義納什均衡的定義,在滿足約束的前提下,當各智能體采取廣義納什均衡策略時,沒有一個參與者可以通過單方面改變策略來降低代價函數.

在無人集群的多聯盟非合作博弈中,需考慮智能體的動力學特性,設智能體的動力學模型為無擾動的二階積分器模型

關于通信拓撲、約束、代價函數有如下假設.

假設1:對于每個智能體聯盟i,聯盟內通信拓撲Gi是無向且連通的,聯盟間通信拓撲也是無向且連通的.

假設2: 局部集合約束Ωij是閉凸集且邊界是分段光滑的,聯盟內耦合代價函數gij是凸函數且二次可微,滿足Slater 條件.

假設4: 對每個智能體,其代價函數時變部分的一階和二階微分是有界的.

為便于求解多聯盟非合作博弈的廣義納什均衡,引入變分不等式問題.

事實上,多聯盟非合作博弈的廣義納什均衡同樣也是上述變分不等式問題（5）的解.

引理1[6]: 在假設3 下,變分不等式問題（5）的任意一個解是多聯盟非合作博弈問題（1）的廣義納什均衡.

引理2[6]: 假設變分不等式問題（5）滿足Slater條件,那么x*是問題（5）的解當且僅當存在乘子,滿足

對比式（6）和式（7）可見,區別在于式（6）中同一聯盟i 中的對偶變量是相同的,即,因此,式（6）是式（7）的特殊情況.前面提到,偽梯度的強單調性保證了基于式（6）得到的廣義納什均衡的唯一性,且該廣義納什均衡屬于滿足式（7）的解的集合,特別地,將該廣義納什均衡稱為變分廣義納什均衡.

本文主要研究多聯盟非合作博弈的變分廣義納什均衡的搜索問題.變分廣義納什均衡的唯一性有利于納什均衡搜索算法的收斂,同時也有著重要的結構和物理特性,即相同的對偶變量可使聯盟中耦合約束帶來的邊界代價對于各個參與者是均衡的.由于多聯盟非合作博弈的代價函數中引入了時變部分,博弈問題的納什均衡不再是固定的點,而是時變的納什均衡軌跡.因此,納什均衡搜索算法要能夠較好地尋找并跟蹤納什均衡軌跡,這也是一個具有挑戰性的難題.

2 多聯盟非合作博弈變分廣義納什均衡搜索問題轉換

在多聯盟非合作博弈的變分廣義納什均衡搜索中,智能體的動力學特性和局部約束的強制性是矛盾的,很難在滿足動態搜索納什均衡的過程中時刻滿足局部約束.本章將設計一種障礙函數處理局部約束,將障礙函數引入代價函數中,從而將局部約束隱含在代價函數中,并得到新的多聯盟非合作博弈問題.

2.1 局部約束的障礙函數

多聯盟非合作博弈問題中參與者具有高階積分器動力學特性或復雜動力學特性,文獻中基于投影動態系統（projected dynamical system）穩定性設計的變分納什均衡搜索算法不再適用.將根據局部集合約束設計障礙函數,使得納什均衡搜索過程始終保持在局部約束范圍內.

即便根據假設2,博弈策略的局部集合約束Ωij具有分段光滑邊界,但是對于一般集合Ωij,很難找到表達其解析表達式.受優化理論中內點方法的啟發,針對集合約束Ωij可設計障礙函數

從式（8）可見,對于某一決策變量xij,障礙函數有限表示決策變量滿足局部約束,障礙函數為正無窮表示決策變量位于約束邊界或不滿足約束.障礙函數可以近似視為某個力場的勢函數,當智能體的決策變量xij靠近約束邊界時,由邊界產生排斥力阻止其繼續接近約束邊界.對于任意形狀的凸集合Ωij,很難找到完美的勢函數,但是,后續分析將證明,式（8）的障礙函數可同樣發揮勢函數的作用,使得決策變量在多聯盟非合作博弈納什均衡搜索中始終滿足局部約束.

對于完美的勢函數,其勢場力為其負梯度方向.當障礙函數作為近似勢函數時,勢場力為,其中,當在xij處可微時,為的梯度;當在xij處不可微時,為的次梯度.障礙函數（8）的性質由以下引理給出.

引理3: 在假設2 下,障礙函數（8）有以下性質:

如果xij在邊界上有多個投影點,那么在xij處不可微,在xij處的次微分是集合的凸包.

2.2 ε-廣義納什均衡

通過引入障礙函數來處理局部集合約束,原多聯盟非合作博弈問題可以轉換為如下的博弈問題

對比問題（1）和問題（10）,可見問題（10）中障礙函數成為各智能體代價函數的一部分,而局部約束則放寬了邊界條件.障礙函數將隱性地起到局部約束的作用,在廣義納什均衡搜索過程中,由于障礙函數的懲罰作用,智能體的決策變量會避免穿越局部集合約束邊界.

后續將求解多聯盟非合作博弈問題（10）,而非問題（1）.由于障礙函數的作用,問題（10）的納什均衡搜索軌跡將始終保持在中,同時根據假設2,Slater 條件依然滿足.

為了說明多聯盟非合作博弈問題（10）和問題（1）的廣義納什均衡之間的關系,下面引入了ε-廣義納什均衡的概念.

下面的定理說明了多聯盟非合作博弈問題（10）的解是問題（1）的一個ε-廣義納什均衡.

定理1: 在假設1-3 下,多聯盟非合作博弈問題（1）和問題（10）均有唯一的變分廣義納什均衡.對于任意的ε>0,存在,使得問題（10）的變分廣義納什均衡是問題（1）的ε-廣義納什均衡.

證明: 在假設2 和3 下,多聯盟非合作博弈問題（1）的策略空間約束滿足Slater 條件,且代價函數偽梯度是強單調的,因此,基于多聯盟非合作博弈問題（1）定義的變分不等式（5）存在唯一解.根據引理1,多聯盟非合作博弈問題（1）的變分廣義納什均衡即為變分不等式（5）的解,同樣滿足存在性和唯一性.

對于多聯盟非合作博弈問題（10）,每個智能體的代價函數改寫為,根據引理3,是凸函數但不一定可微.可建立廣義變分問題: 尋找,滿足

根據式（13）,最終有

進一步,對于任意聯盟i 中任意智能體j,可以定義類似的參數序列,對于任意的ε>0,可以找到一致的N,當選擇n>N 時,以及參數組,多聯盟非合作博弈問題（10）的變分廣義納什均衡是原問題（1）的ε-廣義納什均衡.這個結論很容易利用反證法證明.證畢.

3 分布式變分廣義納什均衡搜索算法設計與穩定性分析

在多聯盟非合作博弈問題框架中,每個聯盟中的智能體通過通信網絡交互信息,并通過動態平均一致性算法,實時估計聯盟代價函數對于各自決策變量的偏微分.采用原對偶方法處理聯盟中的可分耦合約束,每個智能體均需估計各自的對偶變量,并引入了輔助變量zij以確保聯盟內所有智能體對于對偶變量的估計是一致的.

無人集群的多聯盟非合作博弈變分廣義納什均衡搜索算法設計為

定理2: 在假設1～3 下,x*是多聯盟非合作博弈（10）的變分廣義納什均衡,當且僅當存在使得是系統（15）的平衡點,其中,.

是系統（15）的平衡點,則有

根據引理1 和引理2,x*是多聯盟非合作博弈問題（10）的變分廣義納什均衡當且僅當存在滿足下述KKT 條件

因此,下面主要證明條件（16）～條件（19）與條件（20）～條件（21）的等價性.

對上述李雅普諾夫函數函數求導,利用假設3和4,可依次證明級聯系統的輸入狀態穩定,并且系統狀態收斂到納什均衡的鄰域內.

在多聯盟非合作博弈變分納什均衡搜索算法（14）中,直接使用了所有智能體決策變量的完全信息x 和v,所以策略（14）不是完全分布式的.事實上,類似對聯盟代價函數梯度的估計,可以利用領導者-跟隨者一致性算法估計其他智能體的狀態信息,并用來計算代價函數偏微分和約束函數數值.

4 集群時變編隊干擾與反干擾對抗

4.1 集群時變編隊跟蹤的決策－控制架構

本節將介紹多聯盟非合作博弈納什均衡搜索算法在分布式時變編隊控制中的應用.

假設敵我雙方無人集群分別形成一個任務聯盟,每個聯盟內分別有一個領導者,聯盟中跟隨著進行時變編隊跟蹤以完成聯盟任務.在已有文獻中,時變編隊隊形通常是指定的全局信息,本文通過多聯盟非合作博弈納什均衡搜索給出時變編隊隊形決策.假設我方聯盟P1中每個智能體均搭載有電磁干擾裝置,需與聯盟中其他智能體協作以產生對敵方聯盟P2最大干擾效果.聯盟P2則處于防御態勢,盡量形成緊密陣型維持聯盟內通信拓撲的連通性.在這一場景下,兩個聯盟均需協調聯盟內智能體的策略,并找到各自最佳時變編隊隊形.

此外,各聯盟需滿足一些約束條件.要求聯盟中智能體與領導者的平均距離存在最大閾值以減小通信能量損耗.每個聯盟內任意一個智能體有活動范圍限制,該活動范圍是以領導者為圓心,給定半徑的球,從而引入了聯盟中智能體的局部約束.

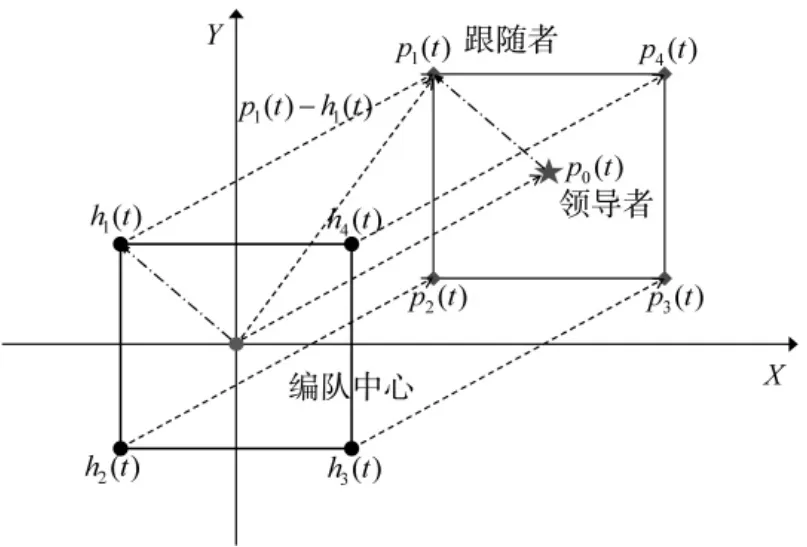
圖1 時變編隊跟蹤示意圖Fig.1 Schematic diagram of time-varying formation tracking

多聯盟非合作博弈變分廣義納什均衡搜索—分布式時變編隊跟蹤控制構成了決策—控制的雙層結構,如圖2 所示.多聯盟非合作博弈變分廣義納什均衡搜索算法給出跟隨者最優編隊構型,隨后由編隊跟蹤控制算法實現.領導者作為獨立節點,是編隊跟蹤的目標,也是編隊構型決策的參考點.

圖2 時變編隊構型決策—編隊跟蹤控制層次結構Fig.2 Hierarchy structure of time-varying formation decisionmaking and formation tracking control

在上述博弈問題的代價函數定義中,假設聯盟P1的領導者是運動的,因此,代價函數與領導者的坐標有關,博弈問題的納什均衡是時變的.基于納什均衡搜索算法（14）以及編隊構型的動力學模型（2）可輸出時變編隊構型,編隊構型的一階導數,以及二階導數,其中,等于納什均衡搜索算法（14）給出的控制量.在此基礎上可設計聯盟P1的編隊跟蹤控制器,在跟蹤的同時實現時變編隊構型的保持.

智能體動力學仍為二階積分器模型,時變編隊跟蹤控制器設計由文獻[2]給出,其形式為:

4.2 仿真算例

在無人集群干擾及反干擾對抗場景以及多聯盟非合作博弈模型基礎上,應用多聯盟非合作博弈納什均衡搜索算法（14）以及編隊跟蹤控制算法（24）,仿真結果如圖3～圖5 所示.圖3 給出了集群博弈對抗雙方軌跡曲線.聯盟P1跟隨其領導者環繞聯盟P2作圓周運動.兩個聯盟根據干擾與反干擾作戰任務和博弈模型實時求解編隊構型,在近似收斂到時變納什均衡后,聯盟P1在其領導者軌跡內側,抵近聯盟P2施加干擾,而聯盟P2則遠離聯盟P1,兩個聯盟的運動形成了環繞聯盟P2中心節點的運動模式.

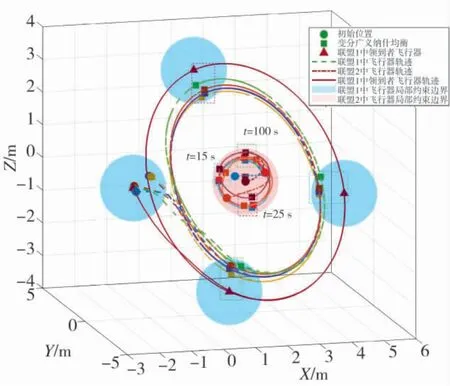
圖3 時變編隊跟蹤干擾-反干擾場景下集群博弈對抗雙方軌跡Fig.3 Trajectories of both sides of cluster game confrontation in the time-varying formation tracking interference and anti-interference scenario

兩個聯盟的狀態曲線如圖4 所示,不同于靜態納什均衡,本例中納什均衡是時變的編隊構型,由于聯盟P1的領導者為規律的圓周運動,可見各聯盟智能體的狀態也是周期性變化.聯盟的耦合約束如圖5所示.由于收斂誤差的存在,聯盟P1、P2的耦合約束圍繞0 附近上下波動.理想結果應當是耦合約束漸進收斂到0,可通過RISE 方法設計納什均衡搜索策略,這會是本文后續的研究方向.

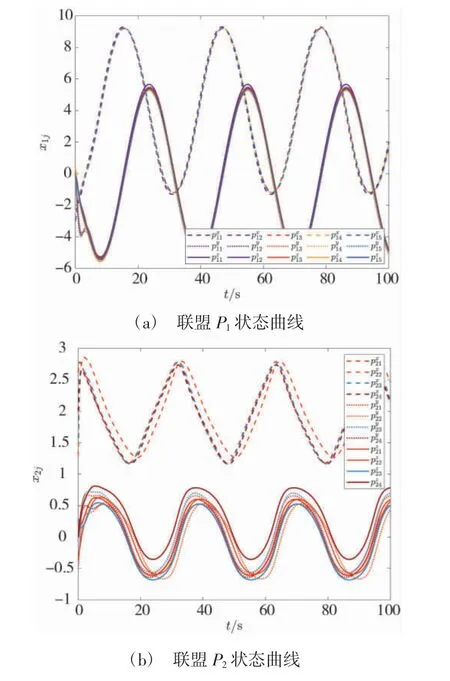
圖4 時變編隊跟蹤干擾-反干擾場景下集群博弈對抗雙方軌跡Fig.4 Trajectories of both sides of cluster game confrontation in the time-varying formation tracking interference and anti-interference scenario

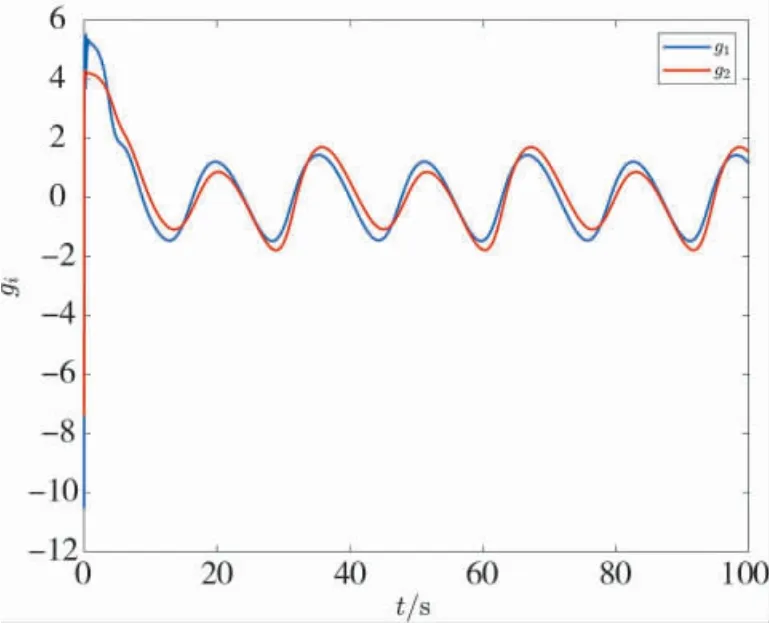
圖5 時變編隊跟蹤干擾－反干擾場景下聯盟耦合約束Fig.5 Coalition coupling constraints of agents in the time-varying formation tracking interference and anti-interference scenario

5 結論

本文研究了嚴苛多約束下多聯盟非合作博弈變分廣義納什均衡搜索算法及其在無人集群博弈對抗中的應用.在多聯盟非合作博弈中,智能體決策變量存在局部約束,以及聯盟內的耦合約束.為使得決策變量始終滿足局部約束,設計了一種障礙函數,其滿足凸性和可微性.隨后,設計了多聯盟非合作博弈變分廣義納什均衡搜索算法,證明了搜索算法的平衡點等價于變分廣義納什均衡點,在多聯合非合作博弈目標函數為時變的情況下,變分廣義納什均衡搜索算法可以收斂到變分廣義納什均衡點的鄰域.最后設計了集群干擾與反干擾的對抗場景,驗證了多聯盟非合作博弈變分廣義納什均衡搜索算法在該場景中的應用能力.