領(lǐng)航者-跟隨者集群系統(tǒng)的隊(duì)形優(yōu)化與控制

陳明飛 王曉東 宋 勛 王 東 王 偉

隨著人工智能、多傳感器信息融合和網(wǎng)絡(luò)通信等相關(guān)技術(shù)的高速發(fā)展,由無(wú)人機(jī)和無(wú)人車等智能設(shè)備組成的集群系統(tǒng)作為未來智能化戰(zhàn)場(chǎng)環(huán)境下的新型武器,受到了中美等軍事強(qiáng)國(guó)的高度關(guān)注.相比于單一個(gè)體,集群系統(tǒng)通過信息傳遞實(shí)現(xiàn)個(gè)體間相互合作,形成優(yōu)勢(shì)互補(bǔ),并借助數(shù)量龐大的優(yōu)勢(shì)在軍事對(duì)抗中占據(jù)主導(dǎo)地位.編隊(duì)控制作為集群系統(tǒng)的重要研究課題之一,已廣泛應(yīng)用于軍事領(lǐng)域,如多架低成本的無(wú)人機(jī)形成固定的隊(duì)形以保護(hù)高價(jià)值的有人機(jī)免受敵方攻擊.相較于集中式控制,基于多智能體架構(gòu)的分布式控制具有去中心化、良好的可擴(kuò)展性和魯棒性等特點(diǎn),已成為國(guó)內(nèi)外的研究熱點(diǎn).

隨著多智能體系統(tǒng)一致性理論發(fā)展,分布式編隊(duì)控制技術(shù)取得了豐富的研究成果[1-12].文獻(xiàn)[1]設(shè)計(jì)基于相對(duì)狀態(tài)反饋的控制器,通過局部信息傳遞,跟隨者與領(lǐng)航者之間保持固定的距離實(shí)現(xiàn)編隊(duì)控制.文獻(xiàn)[3]考慮了通信鏈路故障下的編隊(duì)問題,結(jié)合李雅普諾夫穩(wěn)定性理論和線性矩陣不等式技術(shù),證明設(shè)計(jì)的控制系統(tǒng)是穩(wěn)定的.針對(duì)無(wú)人機(jī)系統(tǒng)存在未知擾動(dòng)的情況,文獻(xiàn)[5]基于有限時(shí)間控制理論設(shè)計(jì)分布式自適應(yīng)控制協(xié)議,減少了跟蹤誤差.文獻(xiàn)[6]考慮了固定翼無(wú)人機(jī)集群在航行過程中存在速度約束和風(fēng)速干擾的情況,設(shè)計(jì)僚機(jī)跟隨長(zhǎng)機(jī)的分布式控制律,實(shí)現(xiàn)編隊(duì)跟蹤控制.針對(duì)固定有向通信網(wǎng)絡(luò)和時(shí)變有向通信網(wǎng)絡(luò)兩種情況,文獻(xiàn)[10]設(shè)計(jì)基于觀測(cè)器的分布式控制協(xié)議,給出時(shí)變編隊(duì)的充分條件.文獻(xiàn)[11-12]分別研究了高階同構(gòu)系統(tǒng)和高階異構(gòu)系統(tǒng)的有限時(shí)間編隊(duì)跟蹤問題.

在上述提到的集群編隊(duì)工作[1-12]中,研究者根據(jù)領(lǐng)航者與跟隨者之間的相對(duì)位置和姿態(tài)等信息,通過設(shè)計(jì)相應(yīng)的控制協(xié)議,使得運(yùn)動(dòng)軌跡滿足預(yù)先設(shè)定的偏移函數(shù).然而,上述文獻(xiàn)并沒有結(jié)合特定實(shí)際的背景衡量隊(duì)形的收益,也沒有判斷集群的隊(duì)形是否為最優(yōu)的.為了獲得集群系統(tǒng)中個(gè)體的最優(yōu)位置,文獻(xiàn)[13]基于博弈論研究了四旋翼無(wú)人機(jī)集群的最優(yōu)位置問題.但每架無(wú)人機(jī)在相互競(jìng)爭(zhēng)的場(chǎng)景下僅衡量自身的收益,獲得的個(gè)體最優(yōu)位置并不意味著整個(gè)集群系統(tǒng)是最優(yōu)的.為了充分發(fā)揮集群協(xié)作的優(yōu)勢(shì),文獻(xiàn)[14]將靜態(tài)的隊(duì)形優(yōu)化問題建模為分布式聚合優(yōu)化問題: 每個(gè)智能體有一個(gè)與自身位置和集群中心位置相關(guān)的目標(biāo)函數(shù),通過局部信息交互衡量集群系統(tǒng)的整體收益,合作構(gòu)建最優(yōu)隊(duì)形.在實(shí)際的跟隨者形成最優(yōu)隊(duì)形環(huán)繞在領(lǐng)航者周圍并抵御入侵者攻擊的情形下,跟隨者的目標(biāo)函數(shù)會(huì)隨著入侵者位置和領(lǐng)航者位置動(dòng)態(tài)變化.因此,關(guān)于時(shí)變目標(biāo)函數(shù)的領(lǐng)航者-跟隨者隊(duì)形優(yōu)化問題亟待進(jìn)一步研究.

受上述工作啟發(fā),本文考慮了領(lǐng)航者-跟隨者集群系統(tǒng)的隊(duì)形優(yōu)化問題,每個(gè)跟隨者不僅需要保護(hù)領(lǐng)航者,還存在威懾入侵者和避障等任務(wù),并基于多智能體分布式優(yōu)化理論,將上述問題建模為在線聚合優(yōu)化問題.通過分布式搜尋全局目標(biāo)函數(shù)的極小值優(yōu)化領(lǐng)航者-跟隨者的隊(duì)形.主要?jiǎng)?chuàng)新點(diǎn)如下:

1）結(jié)合梯度下降法和投影算子,提出了一種固定步長(zhǎng)的離散時(shí)間分布式在線算法.基于矩陣放縮方法,證明設(shè)計(jì)的算法動(dòng)態(tài)遺憾界與常數(shù)項(xiàng)和在線時(shí)間相關(guān).

2）結(jié)合動(dòng)態(tài)平均一致性協(xié)議和梯度追蹤方法,實(shí)現(xiàn)分布式估計(jì)集群系統(tǒng)的中心位置,充分保護(hù)了跟隨者的隱私.

1 預(yù)備知識(shí)與問題描述

1.1 符號(hào)說明

首先介紹本文使用的符號(hào).

Rn表示n 維實(shí)向量空間.1n和0n分別是所有元素均為1 和0 的n 維列向量.定義△g 是函數(shù)g 的梯度以及列向量.表示矩陣A 和矩陣B 的克羅內(nèi)克積.定義為歐幾里得范數(shù).對(duì)于任意的矩陣A 和向量a,則有.表示矩陣A 的譜半徑.

1.2 圖論

1.3 問題描述

考慮領(lǐng)航者-跟隨者集群系統(tǒng)的隊(duì)形優(yōu)化問題,其中,由n 個(gè)跟隨者旨在形成最優(yōu)隊(duì)形保護(hù)領(lǐng)航者免受入侵者攻擊.本文不考慮底層姿態(tài)和機(jī)動(dòng)控制,僅將領(lǐng)航者和跟隨者看作運(yùn)動(dòng)的質(zhì)點(diǎn),采用如下模型描述跟隨者的運(yùn)動(dòng)

在上述問題中,跟隨者i 存在如下的局部目標(biāo)函數(shù)[14-15]:

注2 在集群編隊(duì)問題[5-7]中,跟隨者xi需要與領(lǐng)航者x0之間保持編隊(duì)偏移量di,即.然而,編隊(duì)偏移函數(shù)di往往是根據(jù)先驗(yàn)知識(shí)設(shè)定的.如果偏移函數(shù)設(shè)定較差,則難以充分發(fā)揮集群系統(tǒng)中智能體的互補(bǔ)優(yōu)勢(shì).在問題（2）中,通過求解在線聚合優(yōu)化問題尋找最優(yōu)決策,跟隨者形成最優(yōu)隊(duì)形保護(hù)領(lǐng)航者免受入侵者攻擊.

注3 不同于分布式優(yōu)化問題[16],分布式聚合優(yōu)化問題（2）局部目標(biāo)函數(shù)fi不僅與局部決策xi相關(guān),還依賴于全局聚合信息.此外,在聚合博弈[17]問題中,所有參與者以非合作的方式尋找納什均衡點(diǎn).而問題（2）中跟隨者以合作的方式最小化函數(shù),形成最優(yōu)隊(duì)形.

為了方便后續(xù)分析,給出如下假設(shè).

本文旨在設(shè)計(jì)分布式算法求解在線聚合優(yōu)化問題（2）的極小值,進(jìn)而確定領(lǐng)航者-跟隨者集群系統(tǒng)的最優(yōu)隊(duì)形.

2 算法設(shè)計(jì)與收斂性分析

2.1 算法設(shè)計(jì)

根據(jù)式（1）、式（4）～式（6）,設(shè)計(jì)的算法的緊湊形式如下:

其中,

2.2 收斂性分析

在分析算法（7）的收斂性之前,給出后續(xù)證明中用到的引理.

引理2[14]在假設(shè)2～5 的前提下,對(duì)所有的,則有

引理3[18]假定是一個(gè)非負(fù)不可約矩陣且對(duì)角元素滿足.矩陣M 的譜半徑的充要條件是.

引理4[14]在假設(shè)1 的前提下,存在正數(shù)滿足

下面的引理給出了核心的矩陣不等式關(guān)系.

引理6 在假設(shè)1～5 的前提下,算法（7）的軌跡使得下列不等式成立:

如果步長(zhǎng)α 滿足

整理式（10）,式（13）和式（16）可得式（8）.根據(jù)引理3,計(jì)算行列式

結(jié)合式（18）和式（19）,可得式（9）.根據(jù)文獻(xiàn)[20]中定理6.2.24,由于矩陣M 對(duì)應(yīng)的有向圖是強(qiáng)連通的,則M 不可約矩陣.由引理3 可得矩陣M 譜半徑.證畢.

下面的定理描述了算法（5）動(dòng)態(tài)遺憾界.

定理1 假設(shè)1～5 成立.如果步長(zhǎng)α 滿足式（9）,則動(dòng)態(tài)遺憾界滿足

證明: 首先,遞歸迭代式（8）可得

對(duì)式（21）兩邊同時(shí)取歐幾里得范數(shù)可得

根據(jù)式（3）,動(dòng)態(tài)遺憾界為

因此,可得動(dòng)態(tài)遺憾界RT式（20）.證畢.

,且步長(zhǎng)α 滿足式（9）,則動(dòng)態(tài)平均遺憾界滿足

對(duì)式（25）兩邊同時(shí)取2 范數(shù)可得

由式（23）和式（26）可得

同理,動(dòng)態(tài)遺憾界為

則平均動(dòng)態(tài)遺憾界為

因此,可得平均動(dòng)態(tài)遺憾界式（24）.證畢.

注7 文獻(xiàn)[14]將集群系統(tǒng)的隊(duì)形優(yōu)化問題建模為分布式聚合優(yōu)化問題,通過設(shè)計(jì)離線分布式算法求解全局函數(shù)極小值.然而,文獻(xiàn)[14]的算法無(wú)法處理局部目標(biāo)函數(shù)隨時(shí)間變化的情況.因此,本文將離線的聚合優(yōu)化問題延伸到在線情形,利用矩陣放縮方法分析算法的動(dòng)態(tài)遺憾界.此外,采用動(dòng)態(tài)平均一致性方法,實(shí)現(xiàn)分布式估計(jì)集群系統(tǒng)的中心位置和平均梯度,充分保護(hù)了跟隨者的隱私.

3 仿真算例

考慮由1 個(gè)領(lǐng)航者和4 個(gè)跟隨者組成的集群系統(tǒng)的隊(duì)形優(yōu)化問題,跟隨者相應(yīng)的通訊網(wǎng)絡(luò)如圖1所示.其中,跟隨者形成最優(yōu)隊(duì)形保護(hù)領(lǐng)航者免受入侵者攻擊.在仿真中,僅考慮二維平面的運(yùn)動(dòng)軌跡（可直接擴(kuò)展到多維空間）,設(shè)定運(yùn)動(dòng)區(qū)域約束為,安全距離,權(quán)重系數(shù),,障礙物d0是以為圓心,半徑為0.4 的圓.假定入侵者從運(yùn)動(dòng)區(qū)域外圍向領(lǐng)航者逼近,設(shè)定領(lǐng)航者和入侵者的運(yùn)動(dòng)軌跡為

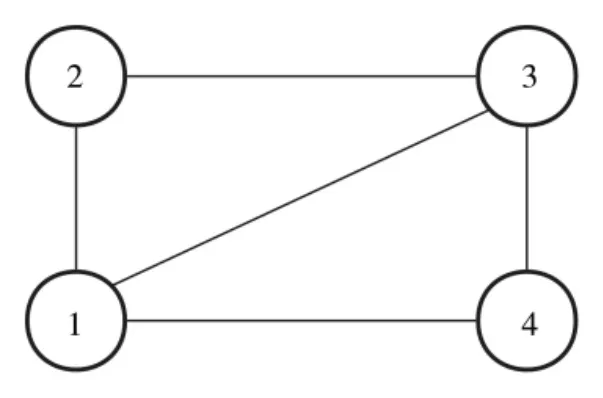
圖1 集群系統(tǒng)的通訊網(wǎng)絡(luò)Fig.1 The communication network of the swarm system

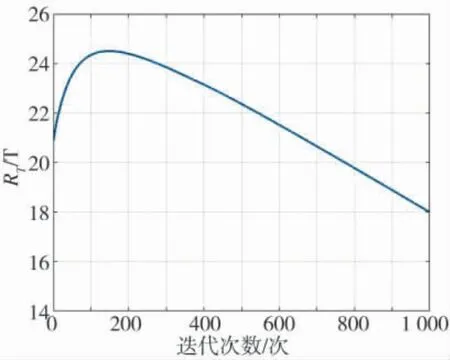
圖2 算法（5）的平均動(dòng)態(tài)遺憾界Fig.2 The evolutions of the average dynamic regret of algorithm（5）

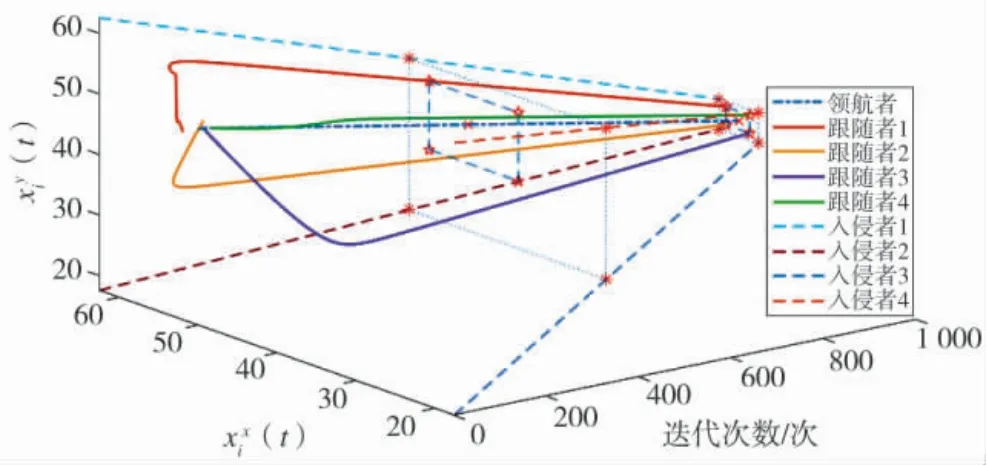
圖3 集群系統(tǒng)的運(yùn)動(dòng)的軌跡Fig.3 Movement trajectories of the swarm system

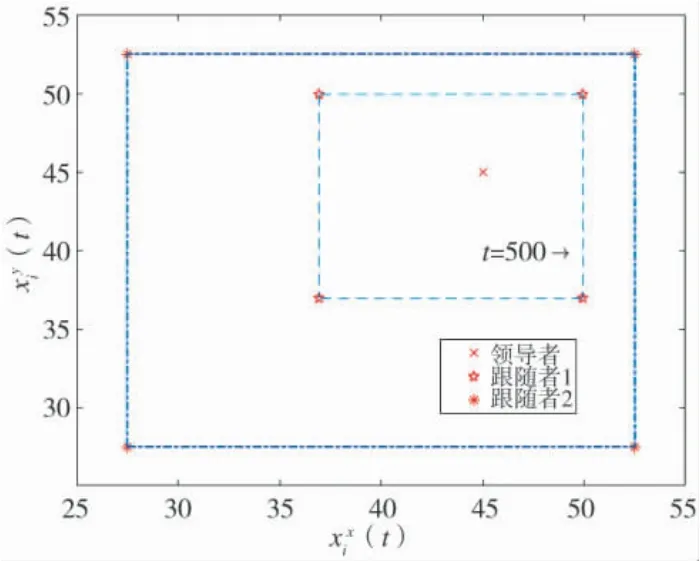
圖4 t=500 時(shí)集群系統(tǒng)的位置Fig.4 Locations of the swarm system at t=500

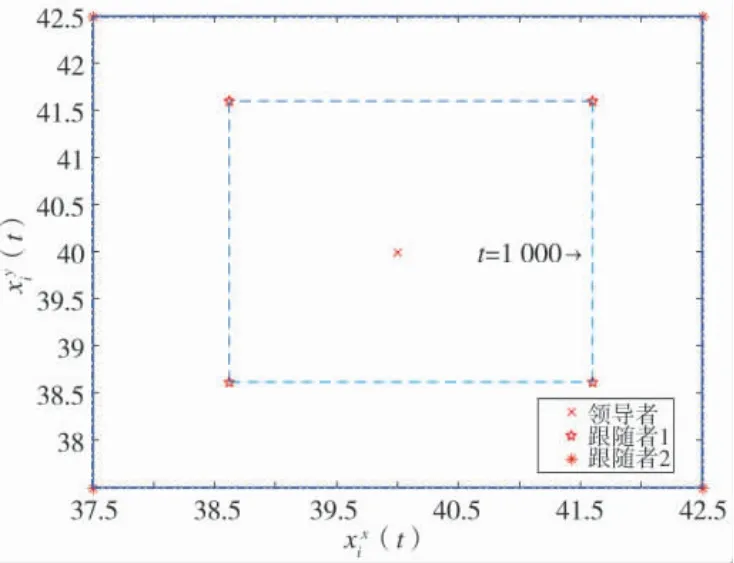
圖5 t=1 000 時(shí)集群系統(tǒng)的位置Fig.5 Locations of the swarm system at t=1 000

4 結(jié)論

本文提出了一個(gè)固定步長(zhǎng)的離散時(shí)間算法解決分布式在線聚合優(yōu)化問題.結(jié)合動(dòng)態(tài)平均一致性協(xié)議和矩陣放縮方法,證明跟隨者軌跡的動(dòng)態(tài)遺憾界與常數(shù)項(xiàng)和在線時(shí)間相關(guān).設(shè)計(jì)的算法為領(lǐng)航者-跟隨者集群系統(tǒng)的隊(duì)形優(yōu)化問題提供了理論依據(jù),具有良好的應(yīng)用價(jià)值.