從古老的方程說起

萬廣磊

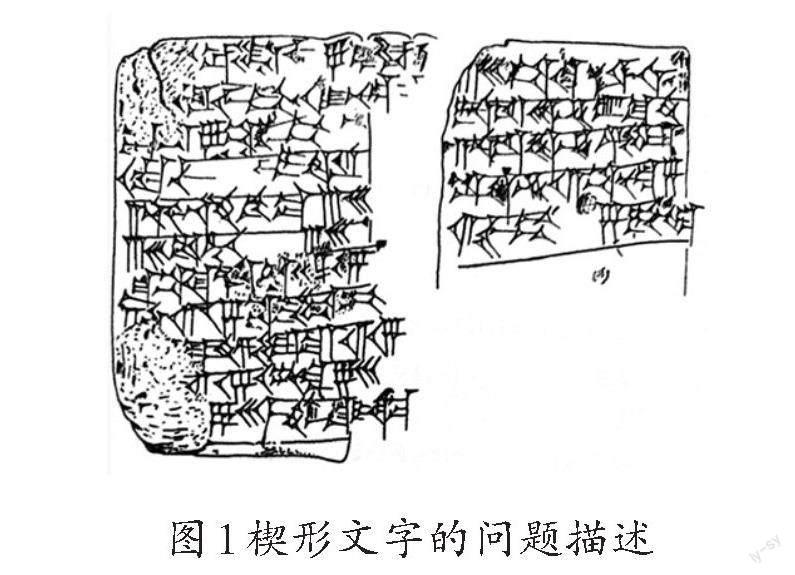
在《楔形文字數學文獻》中有一道數學題，圖1是用楔形文字解釋這道古巴比倫數學題的分析過程，刻在一塊泥板的正反兩面。

除了古代數學史家諾伊格鮑爾和數學家薩克斯的翻譯方法之外，我們用現代方法翻譯一下。這塊泥板上的數學問題大概就是：“一個數比它的倒數大7，這個數是多少？”

有些同學一看到這個問題，會立即寫出方程：x-1/x=7。

但是，我告訴你，你寫錯了。為什么呢？

這是因為古巴比倫的數的進位制與我們現在使用的不一樣。他們用的是“六十進制”，而不是“十進制”。比如，十進制的26表示2個10加6個1，六十進制的26則表示的是2個60加6個1，也就是126。事實上，x的“倒數”可能是60的任何次冪除以x的值，所以，這里x的“倒數”不是我們現在理解的[1/x]，而可能是[60/x]，[3600/x]，等等。不少學者從原作者的求解過程中分析得出，這里的“倒數”應該是[60/x]。所以，正確方程應該是x-60/x=7。

上述方程中，分母含有未知數，我們稱之為分式方程，然后利用等式的基本性質，在方程的兩邊都乘x（x≠0），得到x2-60=7x，再整理，就得到新方程x2-7x-60=0。類比一元一次方程的定義，我們發現這個方程含有一個未知數，且未知數的最高次數是2，二次項的系數不是0。我們將這個方程叫作一元二次方程。

那么這個一元二次方程的x究竟等于多少？將來我們會學習專門的解法，可以得到x=12或x=-5。但是，古巴比倫人不知道負數的存在，所以，他們關心的解是x=12，則它的“倒數”[60/x]的值是5，12-5=7，滿足題意。

1500年前的《孫子算經》中記載了一道數學名題——“雞兔同籠”問題：今有雉兔同籠，上有三十五頭，下有九十四足，問雉兔各幾何？

這四句話的意思是：有若干只雞和兔同在一個籠子里，從上面數，有35個頭，從下面數，有94只腳。請問籠中各有多少只雞和兔？

如果設有x只雞，則兔子有（35-x）只，根據題意，得2x+4（35-x）=94。這是列一元一次方程，同學們在本章已經學習過。

如果設有x只雞，y只兔子，根據題意，得[x+y=35，2x+4y=94。]這是列二元一次方程組，在后續學習中，我們將會遇到。

萬丈高樓平地起。同學們，在初中階段，我們一定要先學好一元一次方程，這樣才可以順利解決其他幾種方程（組）的問題哦！

（作者單位：江蘇省南京市鼓樓實驗中學）