基于虛擬坐標(biāo)的矢量地圖差值擴(kuò)展可逆水印方法

戴 千 一,吳 柏 燕

(湖南科技大學(xué)地理空間信息技術(shù)國家地方聯(lián)合工程實(shí)驗(yàn)室,湖南 湘潭 411201;湖南科技大學(xué)測繪遙感信息工程湖南省重點(diǎn)實(shí)驗(yàn)室,湖南 湘潭 411201;湖南科技大學(xué)地球科學(xué)與空間信息工程學(xué)院,湖南 湘潭 411201)

0 引言

數(shù)據(jù)安全是城市數(shù)字治理的重要前提,數(shù)字成果的應(yīng)用與共享應(yīng)以數(shù)據(jù)安全為基礎(chǔ)。數(shù)字水印技術(shù)能彌補(bǔ)傳統(tǒng)加密技術(shù)限制共享的局限性,在嵌入水印的同時保留原始載體的使用價值[1-3],而在醫(yī)學(xué)診斷、軍事地圖和遙感測繪等特殊場合需要使用無損的高精度數(shù)據(jù),可逆數(shù)字水印應(yīng)運(yùn)而生。可逆水印技術(shù)可在正確提取水印的同時無損恢復(fù)原始載體數(shù)據(jù),避免數(shù)據(jù)永久失真[4]。目前柵格圖像的可逆水印算法較成熟,主要包括基于無損壓縮[5]、直方圖平移[6,7]和差值擴(kuò)展[8,9]3種算法,而矢量數(shù)據(jù)高精度和低冗余的特性使得水印嵌入條件更嚴(yán)格,故柵格圖像的水印算法不完全適用于矢量數(shù)據(jù)[10]。

國內(nèi)外針對矢量數(shù)據(jù)可逆水印的研究大多借鑒圖像水印算法。基于無損壓縮,Celik等[5]提出一種高容量低失真的廣義無損LSB水印嵌入算法,比傳統(tǒng) LSB 方法具有更大的靈活性和更精細(xì)的容量失真粒度。基于直方圖平移,Chen等[7]整合3類直方圖(像素灰度直方圖、差值直方圖和預(yù)測誤差直方圖)平移的優(yōu)勢,采用基于塊的多輪預(yù)測提高了圖像質(zhì)量和水印容量。相比無損壓縮和直方圖平移技術(shù),差值擴(kuò)展技術(shù)具有計(jì)算復(fù)雜度低和易獲得高水印容量的優(yōu)勢,如Wang等[11]首次將差值擴(kuò)展技術(shù)用于矢量地圖數(shù)據(jù)水印,提出基于地圖坐標(biāo)和曼哈頓距離的兩種水印嵌入方案,但因方案水印容量低,頂點(diǎn)相關(guān)性低的地圖在水印嵌入后失真明顯。為平衡水印容量和圖形質(zhì)量,周璐等[12]基于相鄰頂點(diǎn)構(gòu)建坐標(biāo)差值直方圖,利用差值擴(kuò)展嵌入水印,在相同精度容忍度下取得了更高的水印容量和圖形質(zhì)量,但地圖水印容量最高僅為0.5 bit/點(diǎn)。隨后,Peng等[13]改進(jìn)差值擴(kuò)展技術(shù),將水印嵌入二維CAD工程圖所有頂點(diǎn)相對坐標(biāo)的比率集上,提高了水印容量和不可感知性,但若參考頂點(diǎn)逆序提取水印則會破壞水印數(shù)據(jù)完整性。以上研究均為差值擴(kuò)展技術(shù)在矢量數(shù)據(jù)水印上的應(yīng)用,嵌入水印時均重點(diǎn)關(guān)注水印容量和圖形質(zhì)量。此外,部分學(xué)者從可逆性與魯棒性入手提升水印性能。例如:Cao等[14]從載體數(shù)據(jù)入手增強(qiáng)水印可逆性,使用Douglas-Peucker算法提取矢量地圖特征點(diǎn),將非線性加擾后的特征點(diǎn)和非特征點(diǎn)作為載體嵌入水印,算法嚴(yán)格可逆且對地圖簡化攻擊魯棒;佟德宇等[15]提出一種結(jié)合水印區(qū)間定位和區(qū)間內(nèi)部定位的雙重映射機(jī)制,同時對區(qū)間內(nèi)部定位和水印值進(jìn)行校驗(yàn),將校驗(yàn)后的水印信息嵌入坐標(biāo)的可嵌入位中,增強(qiáng)了算法魯棒性;任娜等[16]基于脆弱水印技術(shù)提出通過坐標(biāo)重排序重新建立空間關(guān)系,將當(dāng)前要素所生成的水印信息量化嵌入其他要素中,從而有效避免了要素刪除導(dǎo)致水印信息一同刪除的問題;唐偉[17]提出一種適用于矢量瓦片數(shù)據(jù)的大容量魯棒水印方法:在水印生成階段,分段生成代表組編碼和用戶編碼的水印信息,進(jìn)一步提高水印檢測的正確性,在水印嵌入階段,對經(jīng)典QIM水印嵌入方法進(jìn)行改進(jìn),劃分出更多數(shù)量區(qū)間,水印容量大幅提升;奚旭等[18]為彌補(bǔ)水印容量提升使水印不可見性降低的缺陷,提出量化索引調(diào)制坐標(biāo)點(diǎn)狀態(tài)值嵌入水印,采用MPR(Maximum Perturbation Regions)方法限定坐標(biāo)范圍以控制水印隱蔽性,該方法水印容量大且數(shù)據(jù)擾動程度可控,但算法整體計(jì)算復(fù)雜度較高。

綜上可知,目前矢量數(shù)據(jù)可逆水印研究聚焦于水印容量和數(shù)據(jù)失真問題[13,19-22],水印可逆性和不可見性仍是衡量可逆水印算法性能的重要指標(biāo),如何保持水印容量、水印不可見性及數(shù)據(jù)質(zhì)量的良好平衡是當(dāng)前研究的重點(diǎn)和難點(diǎn)。傳統(tǒng)差值擴(kuò)展技術(shù)應(yīng)用于頂點(diǎn)相關(guān)性低的矢量地圖時,水印容量較低,數(shù)據(jù)失真明顯,導(dǎo)致水印效果不理想。因此,本文提出一種新的矢量地圖差值擴(kuò)展可逆水印方法,即將虛擬坐標(biāo)融入差值擴(kuò)展技術(shù),將水印嵌入差值直方圖平移后的差值中,以解決傳統(tǒng)差值擴(kuò)展技術(shù)應(yīng)用于矢量地圖可逆水印時容量不足及數(shù)據(jù)失真問題。

1 基于虛擬坐標(biāo)的改進(jìn)差值擴(kuò)展技術(shù)

1.1 基于虛擬坐標(biāo)的差值計(jì)算

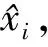
(1)

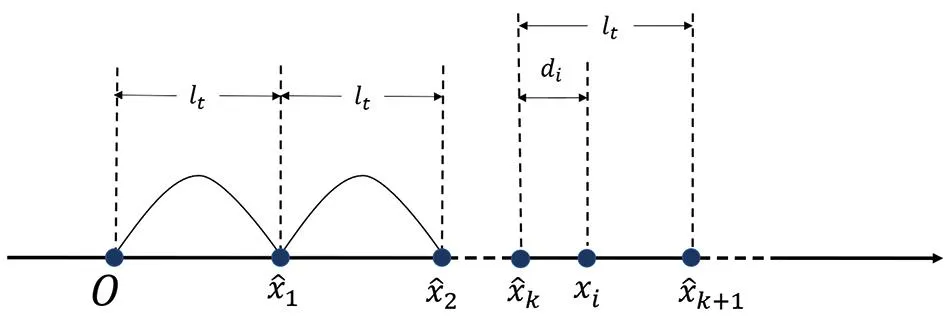
圖1 虛擬坐標(biāo)構(gòu)建差值示意

(2)

(3)

(4)

1.2 參考坐標(biāo)標(biāo)識圖

理論上虛擬坐標(biāo)與實(shí)際頂點(diǎn)重合時,在提取水印時易造成參考坐標(biāo)判斷錯誤,從而導(dǎo)致無法正確提取水印,故僅對不與虛擬坐標(biāo)重合的頂點(diǎn)嵌入水印。提取水印時,差值計(jì)算所基于的參考坐標(biāo)與水印嵌入時應(yīng)保持同步,因此在水印嵌入階段記錄每個實(shí)際頂點(diǎn)的參考坐標(biāo),稱為參考坐標(biāo)標(biāo)識圖,記為L={b1,b2,…,bn},n為地圖頂點(diǎn)個數(shù)。根據(jù)式(5),bi可取值0、1、2,由差值di選取的參考坐標(biāo)及是否與虛擬坐標(biāo)重合兩個條件確定。參考坐標(biāo)標(biāo)識圖能為后續(xù)水印正確提取提供依據(jù),為提高算法效率,對參考坐標(biāo)標(biāo)識圖L采用游程壓縮編碼,壓縮率受區(qū)間步長lt的影響。

(5)

1.3 差值直方圖平移

在基于差值擴(kuò)展嵌入水印時,差值越小,引入的數(shù)據(jù)失真越小。因此,需對差值直方圖進(jìn)行平移,進(jìn)一步降低差值的大小,以減少水印嵌入引入的數(shù)據(jù)失真。差值直方圖峰值所在點(diǎn)記為dmax,則直方圖平移按式(6)進(jìn)行。

d′i=di-dmax

(6)

1.4 水印的嵌入、提取和原始數(shù)據(jù)恢復(fù)

水印嵌入的對象為差值直方圖平移后的差值,水印的提取為水印嵌入的逆過程。為提高算法可讀性,水印的嵌入、提取以及數(shù)據(jù)恢復(fù)以x坐標(biāo)為例說明,y坐標(biāo)的相關(guān)方法和流程與x坐標(biāo)相同。

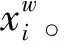
dw′i=d′i×2+w

(7)

(8)

(9)

(10)

(11)

w=dw′i%2

(12)

3)數(shù)據(jù)恢復(fù):①不含水印差值計(jì)算:依據(jù)式(13)計(jì)算不含水印的差值d′i;②差值直方圖逆平移:按式(14)將所有差值d′i向右平移dmax恢復(fù)原始差值di;③原始坐標(biāo)計(jì)算:結(jié)合參考坐標(biāo)標(biāo)識圖L,按式(15)求得原始坐標(biāo)。

d′i=floor(dw′i/2)

(13)

di=d′i+dmax

(14)

(15)

2 基于改進(jìn)差值擴(kuò)展的矢量地圖水印方案

本文算法利用虛擬坐標(biāo)和差值直方圖對傳統(tǒng)差值擴(kuò)展技術(shù)進(jìn)行改進(jìn)(圖2):在水印嵌入階段,首先生成虛擬坐標(biāo),然后對基于虛擬坐標(biāo)計(jì)算的差值直方圖平移,差值擴(kuò)展嵌入水印,形成含水印地圖;水印提取階段,在水印密鑰的輔助下生成與嵌入階段一致的虛擬坐標(biāo),獲取含水印差值,提取水印驗(yàn)證數(shù)據(jù)來源;數(shù)據(jù)恢復(fù)基于差值擴(kuò)展的逆過程,再經(jīng)差值直方圖平移變換求得原始差值,然后計(jì)算原始坐標(biāo),最終恢復(fù)原始地圖。

圖2 本文算法框架

2.1 水印嵌入

(16)

式中:P為小數(shù)點(diǎn)向右移動的位數(shù),Pmax=6。

將區(qū)間長度lt、參考坐標(biāo)標(biāo)識圖L、差值直方圖峰值點(diǎn)dmax、P值保存為密鑰K2,用于后續(xù)水印提取與數(shù)據(jù)恢復(fù)。

2.2 水印提取和數(shù)據(jù)恢復(fù)

以x坐標(biāo)為例,水印提取和數(shù)據(jù)恢復(fù)過程如下:

①遍歷水印地圖Mw所有頂點(diǎn),按式(16)調(diào)節(jié)坐標(biāo),水印提取基于整數(shù)坐標(biāo);②讀取密鑰K2確定區(qū)間步長lt,參照1.1節(jié)生成虛擬坐標(biāo);③利用密鑰K2中的參考坐標(biāo)標(biāo)識圖L,按式(10)計(jì)算含水印差值;④按式(11)將含水印的差值直方圖向左平移;⑤按式(12)提取水印,比較原始水印信息驗(yàn)證數(shù)據(jù)一致性;⑥基于式(13)求出不含水印的差值d′i;⑦按式(14)將差值直方圖向右平移恢復(fù)原始差值di;⑧按式(15)得到整數(shù)化的原始坐標(biāo)xi;⑨解除坐標(biāo)整數(shù)化,獲得原始地圖M。

3 實(shí)驗(yàn)與分析

為驗(yàn)證算法的有效性,在Windows 10操作系統(tǒng)采用Visual Studio 2013開發(fā)平臺進(jìn)行實(shí)驗(yàn)。矢量地圖數(shù)據(jù)由點(diǎn)、線、面要素構(gòu)成,不同類型地圖的數(shù)據(jù)相關(guān)性存在差異,本文選取具有代表性的風(fēng)景名勝POI、等高線、路網(wǎng)和居民地矢量數(shù)據(jù)(圖3)進(jìn)行實(shí)驗(yàn),數(shù)據(jù)格式為Shapefile,基本信息如表1所示。實(shí)驗(yàn)中原始水印圖像為寫有“地理空間”的二值圖像,大小為125×125像素,水印嵌入強(qiáng)度默認(rèn)為1,邏輯映射的初始值k0= 0.635 435。

表1 原始矢量數(shù)據(jù)基本信息

圖3 原始實(shí)驗(yàn)數(shù)據(jù)

實(shí)驗(yàn)選取文獻(xiàn)[11,17,23,24]中的算法作為本文對比算法。其中,文獻(xiàn)[11]是傳統(tǒng)矢量地圖差值擴(kuò)展可逆水印算法;文獻(xiàn)[23]同為虛擬坐標(biāo)在矢量地圖水印的應(yīng)用,但與本文構(gòu)建虛擬坐標(biāo)方法不同;文獻(xiàn)[24]是針對文獻(xiàn)[23]在2維 CAD工程圖的改進(jìn)算法;文獻(xiàn)[17]為矢量瓦片數(shù)據(jù)魯棒水印算法,該算法通過改進(jìn)QIM方法嵌入水印,有效提升了水印容量但不可逆。

3.1 區(qū)間步長lt的討論

本文算法中,確定區(qū)間步長lt是構(gòu)建虛擬坐標(biāo)的前提,不同P值下不同的區(qū)間步長所構(gòu)建的虛擬坐標(biāo)不同,用于水印嵌入的坐標(biāo)差值也不同,區(qū)間步長lt越小,差值越小,基于差值擴(kuò)展嵌入水印后的頂點(diǎn)擾動越小。因此,在相同水印嵌入強(qiáng)度下,區(qū)間步長越小越好。此外,為提升算法的水印容量,虛擬坐標(biāo)與實(shí)際坐標(biāo)的重合概率要盡可能小,因此要求區(qū)間步長盡可能大。綜上,區(qū)間步長的選擇本質(zhì)上是數(shù)據(jù)精度與水印容量的平衡。

3.2 水印容量分析

水印容量即一個數(shù)據(jù)集可嵌入水印數(shù)量的上限,可用平均每個頂點(diǎn)所嵌入的水印比特?cái)?shù)(bit/點(diǎn))表示,即嵌入率。理論上每個頂點(diǎn)的水印容量為2 bit/點(diǎn),本文算法中,水印嵌入在不與虛擬坐標(biāo)重合的坐標(biāo)中,如果部分實(shí)際頂點(diǎn)坐標(biāo)與虛擬坐標(biāo)重合,則重合坐標(biāo)不嵌入水印,此時水印嵌入率小于2 bit/點(diǎn)。由圖4可以看出,4個數(shù)據(jù)集的水印嵌入率均隨lt增大而增大,最大達(dá)到2 bit/點(diǎn),變化速度呈先快后慢趨勢,除風(fēng)景名勝POI數(shù)據(jù)外,在相同lt下,P值越大,水印容量越高;等高線數(shù)據(jù)集首次取得最大水印容量的lt大于其他3個數(shù)據(jù)集,這是由于坐標(biāo)點(diǎn)分布越密集,在相同lt下,與虛擬坐標(biāo)重合的實(shí)際坐標(biāo)越多,水印嵌入率越低;風(fēng)景名勝POI數(shù)據(jù)集由于頂點(diǎn)相關(guān)性較低,受P值變化影響小;當(dāng)lt取最小值時,居民地?cái)?shù)據(jù)集的水印容量最好。

圖4 水印嵌入率與區(qū)間步長lt的關(guān)系

由表2可以看出,當(dāng)區(qū)間步長取合適值時,本文算法水印容量在不同數(shù)據(jù)集中穩(wěn)定為2 bit/點(diǎn),高出文獻(xiàn)[11]的傳統(tǒng)差值擴(kuò)展方法6倍以上。文獻(xiàn)[17]算法水印容量受嵌入位置影響,為便于比較,實(shí)驗(yàn)設(shè)定坐標(biāo)可更改的精度位為6,量化區(qū)間數(shù)為2,即每個坐標(biāo)嵌入一個水印位,水印容量與本文相同且點(diǎn)線面數(shù)據(jù)集均適用。理論上文獻(xiàn)[24]算法迭代次數(shù)可趨近無限,故在不考慮其他水印性能的情況下,文獻(xiàn)[24]算法的水印容量會遠(yuǎn)高于本文算法,但實(shí)驗(yàn)發(fā)現(xiàn)文獻(xiàn)[24]算法應(yīng)用于本文大比例尺地圖時,迭代次數(shù)增加會不同程度地影響水印不可見性和計(jì)算復(fù)雜度,因此對比實(shí)驗(yàn)時迭代次數(shù)設(shè)為1。在同等水印嵌入強(qiáng)度下,文獻(xiàn)[23]與文獻(xiàn)[24]水印嵌入坐標(biāo)數(shù)量相同,故水印容量相同。本文算法水印容量略高于文獻(xiàn)[23,24],這是由于文獻(xiàn)[23,24]算法不能將水印嵌入?yún)⒖甲鴺?biāo)中,而本文算法通過控制區(qū)間步長lt所有頂點(diǎn)均可參與水印嵌入。值得注意的是,雖然POI數(shù)據(jù)集的頂點(diǎn)相關(guān)性很低,但本文算法基于約束的區(qū)間步長lt引入虛擬坐標(biāo),以虛擬坐標(biāo)為參考計(jì)算每個實(shí)際坐標(biāo)的差值,水印可嵌入每個實(shí)際坐標(biāo)中,故水印容量依然很好,而文獻(xiàn)[11,24]在頂點(diǎn)分布稀疏的POI數(shù)據(jù)集中無法嵌入水印。綜上,相對傳統(tǒng)差值擴(kuò)展方法,本文算法擁有更大的水印容量,且顯著降低了頂點(diǎn)相關(guān)性對水印容量的影響。

表2 不同算法水印容量比較(P=6)

3.3 水印不可見性分析

本文從主觀和客觀兩方面評估水印數(shù)據(jù)的不可見性。①主觀上,對嵌入水印后的數(shù)據(jù)與原始數(shù)據(jù)疊加比較,在ArcGIS中進(jìn)行拓?fù)錂z查,未出現(xiàn)要素重疊等問題。觀察圖5發(fā)現(xiàn),正常情況下水印嵌入前后地圖無明顯區(qū)別,局部放大發(fā)現(xiàn)坐標(biāo)點(diǎn)出現(xiàn)微小偏移,但整體沒有出現(xiàn)明顯形變,要素拓?fù)潢P(guān)系保持良好。②客觀上,依據(jù)式(17)和式(18)計(jì)算水印嵌入前后坐標(biāo)點(diǎn)的均方根誤差RMSE(ERMSE)和地圖坐標(biāo)最大改變量Max-R(RMax),二者數(shù)值越小,表示坐標(biāo)偏移越小,水印不可見性越好。由圖6和圖7可知,4個數(shù)據(jù)集的RMSE和Max-R均隨區(qū)間步長lt增大而增大;lt取相同值時,P值越大,同一數(shù)據(jù)集的RMSE和Max-R越小,等高線數(shù)據(jù)在4個數(shù)據(jù)集中的RMSE最小,不可見性最優(yōu);在相同P值下,4個數(shù)據(jù)集的Max-R變化曲線幾乎相同,這是因?yàn)橄嗤琹t下坐標(biāo)構(gòu)建的最大差值相同。風(fēng)景名勝POI數(shù)據(jù)集在P=5時的RMSE與P=6時相差較小,而其他3個數(shù)據(jù)集在P=5時的RMSE與P=4時更接近,P=6時不可見性顯著提升。

(17)

圖5 水印嵌入前后細(xì)節(jié)對比(路網(wǎng))

圖6 Max-R與區(qū)間步長lt的關(guān)系

圖7 RMSE與區(qū)間步長lt的關(guān)系

RMax=max(‖V-Vw‖)

(18)

從表3可以看出,本文算法應(yīng)用于4種數(shù)據(jù)的地圖坐標(biāo)偏移很小,水印不可見性好。文獻(xiàn)[17]作為不可逆水印算法,雖然擁有高水印容量,但水印坐標(biāo)偏移量遠(yuǎn)高于本文算法和其他對比算法。與文獻(xiàn)[11]相比,本文算法的RMSE和Max-R明顯偏低,表明本文算法的坐標(biāo)偏移量更小,圖形質(zhì)量更高,水印不可見性更好;與文獻(xiàn)[23]比較,本文算法應(yīng)用于風(fēng)景名勝POI數(shù)據(jù)的RMSE和Max-R更小,但文獻(xiàn)[23]應(yīng)用于路網(wǎng)數(shù)據(jù)的不可見性與本文算法相差不大;文獻(xiàn)[24]應(yīng)用于等高線和路網(wǎng)數(shù)據(jù)的不可見性略差于文獻(xiàn)[23],原因是文獻(xiàn)[24]的水印坐標(biāo)受虛擬坐標(biāo)區(qū)間狀態(tài)值影響;此外,本文算法在4種數(shù)據(jù)集中的RMSE相差不大,即使對頂點(diǎn)相關(guān)性低的POI數(shù)據(jù)集,也取得了與其他3個數(shù)據(jù)集相當(dāng)?shù)腞MSE結(jié)果,這是因?yàn)樘摂M坐標(biāo)的構(gòu)建提高了數(shù)據(jù)相關(guān)性,差值直方圖平移減小了坐標(biāo)擾動,整體上可嵌入水印的數(shù)據(jù)單元增加而數(shù)據(jù)失真保持在較小范圍。

表3 不同算法水印不可見性比較(P=6)

本文算法實(shí)驗(yàn)中,1∶1 000的原始地圖和水印地圖之間的最大Max-R為 0.000 285 19<0.30 m(國標(biāo)《1∶500 1∶1 000 1∶2 000外業(yè)數(shù)字測圖技術(shù)規(guī)程 GB14912—2005》中的地形圖精度平面誤差要求),符合實(shí)際生產(chǎn)標(biāo)準(zhǔn),其他4個測試數(shù)據(jù)的水印地圖數(shù)據(jù)精度也均滿足應(yīng)用要求,因此,本文算法嵌入水印所引起的數(shù)據(jù)擾動不會影響矢量地圖的可用性。

3.4 可逆性分析

為評價恢復(fù)地圖客觀質(zhì)量,計(jì)算不同算法下原始矢量地圖與恢復(fù)后矢量地圖之間的RMSE和Max-R值(表4)。通常矢量地圖數(shù)據(jù)存儲精度約為0.1 mm,實(shí)驗(yàn)中原始坐標(biāo)與恢復(fù)坐標(biāo)之間的差異小于10-4m即認(rèn)為方案可逆。理論上本文算法可以在正確提取水印的基礎(chǔ)上無損地恢復(fù)原始地圖,這是由本文算法機(jī)制決定的:本文算法和文獻(xiàn)[11]算法是基于整數(shù)坐標(biāo)進(jìn)行運(yùn)算,小數(shù)部分不參與水印嵌入,因此水印嵌入后的精度在運(yùn)算過程中并無損失;另一方面,水印嵌入和數(shù)據(jù)恢復(fù)時差值直方圖經(jīng)過兩次平移變換,兩次變換互為逆運(yùn)算,不會對地圖坐標(biāo)產(chǎn)生影響。文獻(xiàn)[24]算法中,水印坐標(biāo)含有失真參數(shù)Q,會影響水印提取恢復(fù),文獻(xiàn)[17]為魯棒水印算法,無法從水印地圖中恢復(fù)出可用的地圖,因此算法不可逆。由表4可知,基于文獻(xiàn)[23,24]算法的RMSE和Max-R雖然不為0,但數(shù)值極小,對地圖數(shù)據(jù)質(zhì)量的影響很小,因此也認(rèn)為是可逆算法;從可逆性上看,文獻(xiàn)[11]算法與本文算法最優(yōu)。

4 結(jié)束語

本文基于傳統(tǒng)差值擴(kuò)展技術(shù)引入虛擬坐標(biāo)計(jì)算差值,將構(gòu)建的差值直方圖平移,通過差值擴(kuò)展將水印信息嵌入坐標(biāo),與傳統(tǒng)差值擴(kuò)展方法(文獻(xiàn)[11])相比,有效提升了水印容量并減小數(shù)據(jù)擾動。與文獻(xiàn)[23,24]的方法相比,本文算法虛擬坐標(biāo)由區(qū)間步長lt構(gòu)建,無需浪費(fèi)參考坐標(biāo)。同時,本文算法對于頂點(diǎn)相關(guān)性低的地圖數(shù)據(jù)(如POI數(shù)據(jù))同樣適用,可以實(shí)現(xiàn)大比例尺地圖的水印嵌入,在實(shí)際工程建設(shè)中具有現(xiàn)實(shí)意義。

本文未涉及高強(qiáng)度嵌入水印的情況,對于單個水印嵌入單元能否攜帶大量水印信息也欠考慮。因此,提升可逆水印算法的魯棒性和探討高水印嵌入強(qiáng)度的水印算法可行性是下一步的重點(diǎn)研究內(nèi)容。