基于相似圖投影學習的多視圖聚類

趙偉豪 林浩申 曹傳杰 楊曉君

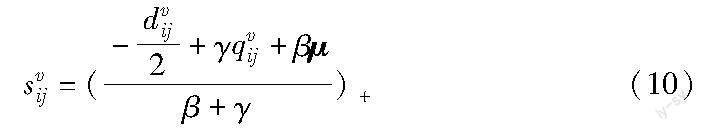
摘 要：隨著數據來源方式的多樣化發展，多視圖聚類成為研究熱點。大多數算法過于專注利用圖結構尋求一致表示，卻忽視了如何學習圖結構本身;此外，一些方法通常基于固定視圖進行算法優化。為了解決這些問題，提出了一種基于相似圖投影學習的多視圖聚類算法（multi-view clustering based on similarity graph projection learning，MCSGP），通過利用投影圖有效地融合了全局結構信息和局部潛在信息到一個共識圖中，而不僅是追求每個視圖與共識圖的一致性。通過在共識圖矩陣的圖拉普拉斯矩陣上施加秩約束，該算法能夠自然地將數據點劃分到所需數量的簇中。在兩個人工數據集和七個真實數據集的實驗中，MCSGP算法在人工數據集上的聚類效果表現出色，同時在涉及21個指標的真實數據集中，有17個指標達到了最優水平，從而充分證明了該算法的優越性能。

關鍵詞：多視圖聚類； 投影學習； 相似圖； 圖融合

中圖分類號：TP391?? 文獻標志碼：A?? 文章編號：1001-3695（2024）01-016-0102-06

doi：10.19734/j.issn.1001-3695.2023.05.0195

Multi-view clustering based on similarity graph projection learning

Abstract：With the diversified development of data sources， multi-view clustering has become a research hotspot. Most algorithms focus too much on using graph structure to seek consistent representation， but ignore how to learn the graph structure itself. In addition， some methods are usually optimized based on fixed views. In order to solve these problems， this paper proposed a multi-view clustering algorithm based on similarity graph projection learning（MCSGP）， which effectively fused the global structure information and local potential information into a consensus graph by using the projection graph， rather than only pursuing the consistency of each view with the consensus graph. By imposing a rank constraint on the graph Laplacian matrix of the consensus graph matrix， this algorithm could naturally divide the data points into the required number of clusters. In the experiments on two artificial datasets and seven real datasets， the MCSGP algorithm shows excellent clustering effect on artificial data sets. At the same time， in the real datasets involving 21 indicators， 17 indicators reach the optimal level， which fully proves the superior performance of the proposed algorithm.

Key words：multi-view clustering; projection learning; similarity graph; graph fusion

0 引言

隨著現代信息技術的發展，信息獲取途徑不斷增多，人們從社交媒體、移動應用程序到各種傳統媒體中收集數據的形式也變得越來越多樣化，例如一個圖片存在HOG特征、LBP特征和Haar特征等多種類型的圖像特征。在人們的日常生活中，由于信息不足，若僅基于一個圖像特征對圖像進行聚類會導致聚類性能降低。由于可以從數據的不同視圖中獲得不同的信息，多視圖聚類所獲得的信息量遠大于單視圖聚類。在多視圖聚類中，如何提取有用的信息并綜合不同視圖的信息進行聚類，已成為一個挑戰。

多視圖聚類算法是一種處理多源異構數據的有效方法，在這個過程中，研究人員采用不同的思路和技術去融合有用的信息來提高整體的聚類性能。現有多視圖算法大致可分為多視圖協同訓練算法、多視圖共正則化算法、多視圖多核聚類算法、基于子空間多視圖聚類算法、基于圖的多視圖聚類算法等。

在考慮多視圖一致性問題下，協同訓練算法被廣泛研究和應用，這類算法旨在最大限度地實現所有觀點（視圖）達成一致，達到最廣泛的共識。此外，研究人員也研究了協同訓練算法的多個擴展版本，如co-EM［1］、聯合正則化［2］、聯合聚類［3］等。多核學習最初是為了擴大核函數搜索空間，以提高模型的泛化能力。傳統的核學習算法通常使用固定的核函數，如線性核、多項式核和高斯核等。基于多核學習的多視圖聚類旨在優化組合一組預定義的核，以提高聚類性能。在這類算法中，一個核心問題就是如何選擇合適的核函數，并將這些核函數進行最優的組合以完成聚類任務。在單視圖場景下基于最大間隔聚類［4］，Zhao等人［5］提出了一種多核聚類算法，可以同時找到最大間隔超平面、最佳聚類和最優核。De Sa等人［6］基于最小化不一致性算法構建了自定義核組合方法。Yu等人［7］將經典的K-means聚類擴展到Hilbert空間，其中多視圖數據矩陣被表示為核矩陣，然后自動組合用于數據融合。低秩張量約束多視圖子空間聚類是由Zhang等人［8］提出的一種基于子空間的多視圖聚類算法，該算法借助潛在空間的理論，假設存在一個多視圖數據可以共同表示的潛在表示，將多個視圖的數據映射到潛在表示下，利用潛在表示的聯系和互補性進行聚類。其中，子空間聚類算法常用的方法包括子空間學習［9～11］和非負矩陣分解。子空間學習通常假設每個視圖的數據分布在一個低維子空間中，而非負矩陣分解則假設數據可以表示為非負基向量的線性組合。Xu等人［12］提出了一種新的帶有平滑權重的自定步長算法，該算法繼承了logistic函數的優點，并提供了概率權重，以緩解局部極小值問題。雖然這些多視圖算法［13～17］在不同的數據集下取得了較好的結果，但依然存在下面幾個問題：a）目前多視圖譜聚類算法中大部分采用預先構造一個共識圖的方法，這種方法首先利用其他單視圖算法獲取每個不同視圖的相似圖，然后固定這些相似圖執行聚類融合任務，未能很好地利用不同視圖的信息互補性以更新相似圖；b）以往許多研究都集中在共識圖與不同視圖相似圖之間的差異，并采用加權策略來調整視圖權重，然而這種差異本身就是存在的，若過度關注于同視圖相似圖和共識圖的本身差異，則會忽略兩者之間的關聯性；c）不同視圖形成相似圖的概率本身并沒有精確地描述數據之間的關系，而是表征了一種可能的關系，這種關系更多地反映了整體數據的部分信息映射到相似圖中的結果。不同視圖提供的信息是由整體數據的總信息與某種關系共同作用的結果，但是這種關系并未得到充分的展現。

為了解決上述問題，本文提出一種基于相似圖投影學習的多視圖聚類（multi-view clustering based on similarity graph projection learning，MCSGP）。a）該算法將投影學習和多視圖譜聚類融合為一個框架，并聯合優化投影矩陣、局部相似學習和多視圖譜聚類，通過這種方式有助于獲得可靠性高的相似度圖，并最終提高聚類性能；b）該算法采用了互相促進的方法來學習每個視圖的圖和共識圖，而非使用固定的相似圖，從而進一步提高了聚類的性能，具體而言，該方法通過投影圖將不同視圖上的信息融合在共識圖中，而不再是專注地利用圖結構尋求一致表示，運用投影圖去學習圖結構本身，借助投影圖減少了視圖之間的互補性信息，不會產生共識圖丟失重要信息的影響，因此該算法能夠保證每次更新后視圖的互補性信息不會大量減少，并將視圖信息也融合到共識圖中，以促進學習到的共識圖更好地分為不同的聚類簇；c）為了求解聯合優化問題，設計了一種有效的交替迭代方法。實驗結果表明，MCSGP算法在人工數據集和真實數據集中均表現出了較好的性能，證明了其優越性。

1 相關工作

1.1 符號定義

1.2 自適應鄰居聚類

譜聚類是一種基于圖論和矩陣分析的無監督學習算法，在處理非凸、非線性的數據中獲得的聚類效果較好。譜聚類的構造方式可以通過調整相似度矩陣或拉普拉斯矩陣來適應不同的數據類型和聚類需求。在譜聚類中，構造鄰接矩陣時，對于每個邊的權重需要用高斯核函數來構造。Nie等人［18］提出在自適應近鄰學習中，通過對每個數據點分配基于局部連通性的自適應和最優鄰居來學習數據相似度矩陣S，并用實驗驗證相似度矩陣稀疏會對噪聲具有魯棒性，極大地提高了聚類效果。目標函數為

s.t.i， sTi1=1，0≤si≤1，F∈RApn×c，FTF=I（1）

其中：拉普拉斯矩陣LS=D－（S+ST）/2；度矩陣D是一個對角矩陣，其對角線第i個元素dii=（sij+sji）/2；F∈RApn×c是譜嵌入矩陣，由LS矩陣的c個最小特征值對應的特征向量組成，c是聚類的類別數。上述自適應近鄰學習（CAN）的單視圖聚類算法可直接使用在多視圖聚類中，故目標函數為

其中：svij是第v個視圖中相似度矩陣Sv里的第i行、第j列的元素。過去的研究［18］表明，通過樣本間的局部相似性可以更準確地刻畫樣本之間的關系。

1.3 相似圖學習

在多視圖聚類的圖形學習中，MVGL［19］提出了構建共識圖的思路，首先對每個視圖運用CAN算法，得到每個視圖的相似圖Sv，然后從多個視圖的相似圖中學習得到一個統一的共識圖A，最后對共識圖進行一個拉普拉斯秩約束。在基于圖的多視圖聚類中，對MVGL進行了改進。GMC［20］模型首先在每個視圖的原始樣本空間Xv分別學習到自身視圖的相似度誘導圖Sv，為了融合不同視圖的相似圖，GMC引入了一個共識的相似度圖U，并使每個Sv盡可能地與U達到一致，主要是將視圖的一致性信息融合進去。其中wv使每個視圖都是自動加權的，并且相似圖矩陣和統一圖矩陣是聯合學習的，以便它們能夠以相互加強的方式相互幫助。考慮到每個視圖的貢獻可能是不同的，GMC的目標函數為

其中：U是學習得來的共識相似度矩陣。這里忽略每個視圖的相似度圖可能本身差異性就較大，而使用的約束是wv‖U－Sv‖2F，該約束項側重于增強視圖之間的共性，以盡可能使每個視圖的自身相似圖一致，但是沒有充分利用視圖之間的差異性。在更新過程中，視圖的相似圖由于趨于一致而損失了自身視圖的信息量，這可能會影響下一次更新共識圖矩陣的準確性。為了更好地利用視圖間的互補性信息，在每次更新過程中需要保持視圖的互補性信息不減少。

2 MCSGP聚類算法

2.1 MCSGP模型

為了將每個視圖的相似圖學習到一起，MCSGP算法也將引入一個共識的相似度圖U，并且假設每個視圖的相似度圖Sv是由共識相似度圖投影得到的，本文模型使用核范數來度量誤差，所構建的約束為

其中：Pv是投影矩陣。每個視圖樣本之間的關系主要是通過將整個共識圖樣本之間的關系投影到視圖空間中獲得的，這樣可以避免每個視圖的相似圖逐漸趨于一致的問題，并且減少了在更新過程中損失視圖間互補性信息的風險。此外，這種方法還可以獲得每個視圖中的信息，并將其融合到共識圖中。為更好地將共識相似度圖合理地劃分為c個聚類簇，在GMC算法啟發下，本文也引入rank（LU）=n－c約束項，其中LU=DU－（U+UT）/2。矩陣的秩約束直接求解并不能有效地得到目標函數的解。令υi（LU）為LU的第i個最小的特征值。由于LU

其中：β、γ、λ是目標函數的超參數，用于平衡每個約束項之間的權重。在整體的目標函數中，本文通過投影關系將多視圖數據的共識相似圖與每個視圖的相似圖融合在一起。此外，多視圖相似度圖和共識圖之間的相互學習可以改善不同視圖與共識圖的映射關系，并且能夠生成更符合實際映射關系的投影圖。接下來，采用一種交替迭代優化方法（alternating direction method of multipliers，ADMM）來求解式（5），即目標函數。

2.2 優化求解

本文提出的多視圖聚類模型的目標函數是高度耦合的，難以一次性求解每個變量。為了解決這個問題，本文將目標函數分解為四個子問題，并采用交替迭代優化方法對每個變量進行優化求解。通過這種方式可以有效地降低問題的復雜度，提高求解效率，并且保證每個變量的優化問題都能得到充分的考慮和處理。

1）固定Pv、U、F，更新Sv 當其余參數固定時，目標函數最后一項變為常量，目標函數等價于

注意到式（6）中不同的i對應的svi之間是相互獨立的，因此可以對每個svi分別求解該問題。

定義dvij=‖xvi－xvj‖22和Qv=PvU，將qvi∈RApn×1定義為向量，屬于Qv中的第i列。式（6）可以寫成向量的形式：

由式（7）根據現有的約束項構建拉格朗日函數：

其中：μ為拉格朗日系數標量;ξ為拉格朗日系數向量。由上式對svi求導并令求導為零，即得到

根據Karush-Kuhn-Tucker（KKT）條件求解得到

根據文獻［21］中的解法，限制svi有k個非零元素，則

又因約束條件1Tsvi=1，則

由式（11）（12）綜合可得

為了約束svi有k個非零元素的最優解，可得

根據式（11）（12）（14），聯立可得Sv最終的更新公式為

2）固定Sv、U、F，更新Pv 當其余參數固定時，目標式（3）只有第三項依然是變量，目標函數等價于

對于任意矩陣，‖M‖2F=Tr（MMT）都成立。可將式（16）推導為

通過簡單替換，模型變為

其中：A=UUT，B=USv。為了求解式（18），本文引入文獻［22］中的定理來解決此模型。可以將式（18）中的Stiefel流形上的二次問題進一步松弛為

其中：W=（Pv）T，通過式（20）對W求導為0，且由文獻［22］可得到

定理1 用UΣVT表示M∈RApm×n的奇異值分解，則Z=UVT是式（19）的解。

arg max Tr（ZTM）

s.t. ZTZ=I（22）

其中：UTU=VTV=Ir;Σ∈RApr×r為非奇異對角矩陣，其對角線上的元素為矩陣B的奇異值λi；r=rank（M）。

根據定理1，式（18）的最優解為

Pv=WT=（UVT）T（23）

其中：U和V是M的左、右奇異向量矩陣。

3）固定Sv、F、Pv，更新U 當其他參數固定時，目標式（5）可推導為

由于Pv是投影矩陣，且符合（Pv）TPv=I，而且投影矩陣是固定的，可繼續優化公式得

由于‖AB‖F≤‖A‖F‖B‖F和‖Pv‖F=‖（Pv）T‖F，式（26）的第二部分一起優化，將矩陣轉換成矩陣各個元素即

其中：dfij=‖fi－fj‖22，Ev=PvSv，evij是矩陣Ev中第i行、第j列的元素。因式（27）的變量為U，‖Pv‖2F是一個固定量，可當做常數。注意到問題對不同的i是獨立的，因此對每個ui分別求解式（27），可優化為

進一步將dfi表示為向量，對應第j個元素為dfij，將evi表示為向量，對應第j個元素為evij。將問題等價于求解如下問題：

4）固定Sv、Pv、U，更新F 優化問題即為解決以下問題：

則最優解F由拉普拉斯矩陣LU最小c個特征值對應的c個特征向量組成。算法1總結了MCSGP的所有操作流程。

5）初始化 在實際實驗過程中，本文初始化相似圖（SIG）矩陣，每個視圖的SIG矩陣是獨立的，這里以Sv為例。

其中：bvij=‖xvi－xvj‖22和k是近鄰個數。設投影矩陣Pv初始化為單位矩陣，共識相似圖矩陣U為

算法1 MCSGP

輸入：具有m個視圖的多視圖數據集{Xv}mv=1，聚類數c，初始化參數β、γ、λ。

輸出：Sv、Pv、U，F。

初始化：通過式（31）（32）（30）來初始化Sv、U、F以及初始化Pv為單位矩陣；

重復執行：

通過式（15）來優化Sv；

通過式（23）來優化Pv；

通過式（29）來優化U；

通過式（30）來優化F；

直到目標函數收斂

2.3 復雜度分析

本節分析MCSGP算法的計算成本，該算法主要由相似圖構造、投影圖構造、共識相似圖構造和譜聚類四部分組成。對應的復雜度分別為O（mnk），O（m3n3），O（cn），O（cn2）。其中m代表視圖數，n代表樣本數，c代表聚類，由于n>>m并且n>>c，本文算法的復雜度主要計算投影圖的構造過程。

3 實驗結果與分析

3.1 人工數據集實驗

本文使用了兩個被廣泛應用的人工數據集，分別是：a）TwoMoon數據集，由兩個視圖組成，每個視圖包含兩個月球形簇，添加0.12%的高斯隨機噪聲，每個類別包含100個樣本點；b）ThreeRing數據集，由三個視圖組成，每個視圖都由三個同圓心但不同半徑的圓組成，并且添加了隨機高斯噪聲，每個類分別包含30、90和180個樣本點。

圖1和2顯示了TwoMoon和ThreeRing中兩個視圖的聚類過程。圖2（b）展示了兩個視圖最原始的相似矩陣構造圖，兩個類之間的數據點是有連接的部分，說明類群之間的相連不易分離；圖2（c）展示了兩個視圖通過目標函數迭代學習到的相似矩陣構造圖，可以發現，其與圖2（b）部分數據點之間的邊被削弱，部分邊被對應地加強；圖2（d）展示了三個圓形聚類得到了很好的分離，這是因為MCSGP算法通過投影圖，充分利用了不同視圖相似矩陣的差異性信息，并在共識圖中融合它們。在人工數據集上的實驗結果表明，本文算法能夠很好地融合不同視圖的信息互補性，利用投影圖可以最大程度地保留每個視圖的信息，同時在共識圖中融合這些信息，從而實現視圖間的信息交互。

3.2 真實數據集實驗

本節旨在對七個真實的多視圖數據集進行評估，以驗證本文算法的有效性。表1介紹了這些數據集的相關信息。

a）BBC數據集，它是一個包含685篇文章的合成文本數據集，這些文章來自BBC新聞網站。每個文檔分為四個部分，對五個主題標簽中的一個進行人工標注。

b）100Leaves數據集，它是一個包含16種不同植物葉片的數據集，每種都有100個樣本。對于每個樣本，給出了形狀描述符、細比例邊界和紋理直方圖。

c）ORL數據集，它是一個包含400張不同人臉的圖像數據集，是由英國劍橋的Olivetti研究實驗室在1992—1994年期間創建的。該數據集包括40個不同人的圖像，每個人有10張圖像，此外，該數據集還包括4個視圖。

d）MSRC_v1數據集，它是一個包含210張圖像和7個類的數據集，數據來自劍橋微軟研究院，是帶有粗粒度標記的圖像。

e）3sources數據集，它是包含169條新聞組成的多視圖文本語料庫。該數據集由三個在線新聞服務的文章組成，包括英國廣播公司、路透社和《衛報》的三個視圖，每個視圖有169個新聞，共分為6個類別。

f）WebKB數據集，它是包含四所大學的計算機科學系收集的網頁數據，共4個類別以及203個網頁樣本。每個網頁通過頁面的內容、超鏈接的錨文本以及標題中的文本進行描述。

g）HW2sources數據集，它是一個包含2 000個手寫數字的圖片數據集，來自UCI存儲庫，其中每個樣本都是手寫數字之一（0～9）。數據來源于HW數據集里的兩個視圖。

用于比較的11種多視圖聚類算法分別是SC_best、基于聯合非負矩陣分解的多視圖聚類（multi-view clustering via joint nonnegative matrix factorization，MultiNMF）［24］、譜聚類的親和聚合（affinity aggregation for spectral clustering，AASC）［25］、自適應加權過程進行多視圖聚類（multiview clustering via adaptively weighted procrustes，AWP）［26］、共正則化多視圖光譜聚類（co-regularized multi-view spectral clustering，CoReg）［27］、多視圖共識圖聚類 （multiview consensus graph clustering，MCGC）［28］、多視圖聚類的圖形學習（graph learning for multiview clustering，MVGL）［19］ 、基于低秩和稀疏分解的魯棒多視角譜聚類（robust multi-view spectral clustering via low-rank and sparse decomposition，RMSC）［29］、基于圖的多視圖聚類（graph-based multi-view clustering，GMC）［20］、基于深度非負矩陣分解的多層流形學習多視圖聚類（multi-layer manifold learning for deep non-negative matrix factorization-based multi-view clustering，ODD-NMF）［30］、基于集成的快速多視圖聚類（fast multi-view clustering via ensembles： towards scalability，superiority，and simplicity）［31］。其中SC_best是在真實數據集中每個視圖實驗過程中進行譜聚類，取單個視圖中最好的聚類效果。為了減少部分對比算法初始化帶來的隨機性，將每種對比算法重復執行10次，并取其平均聚類效果值，本文算法和對比算法在真實數據集的聚類性能結果如表2～4所示。

3.3 聚類實驗結果

在本次實驗中，對樣本數據進行歸一化處理，并采用三種常用的評價指標，即準確度（accuracy，ACC）、歸一化互信息（normalized mutual information，NMI）、純度（purity，PUR）。對于這三個指標，數值顯示越高，證明聚類性能越好。如表2～4所示，在這次實驗過程中，對相同數據集的實驗性能，不同算法聚類性能最優算法用黑體加粗，次優算法加下畫線。具體來看，在ORL、MSRC_v1、WebKB、BBC和HW2sources數據集上，顯示了本文算法優于其他對比算法，三個指標都占優。在BBC、100Leaves和3sources數據集上顯示本文算法在部分指標上占優，尤其是3sources和WebKB數據集，準確度遠遠領先于次優算法，分別提高了6.51%和6.77%。在WebKB數據集中，MCSGP算法在互信息量指標下的聚類效果也顯著優于其他算法，該算法能夠學習到樣本間的局部相似性以及視圖間的互補性，將每個視圖的互補性信息映射到共識相似矩陣中，從而獲得一個更優的聚類效果。

3.4 參數敏感性分析

在本文實驗過程中，有三個超參數需要手動調整，分別是視圖正則化參數β、視圖投影權重系數γ、譜聚類權重參數λ。為了直觀地說明參數對聚類性能的影響，本文在BBC數據集上進行了基于ACC和NMI的參數分析實驗。三個參數在［50：10：100］遍歷。實驗結果如圖3所示。實驗固定一個參數，測試另外兩個參數的敏感性，從圖3可以看出，三個參數對算法準確度和互信息量影響不大，表明本文方法的性能對參數不敏感。在其他數據集上的實驗也得出類似結論，說明本文算法穩定可靠，但仍需根據具體情況調整參數，以達到最佳性能。

3.5 收斂性分析

本節主要負責驗證目標函數能否達到收斂。圖4展示了迭代目標函數與迭代次數的關系，本文算法的目標函數在七個數據集中，在前15次迭代就已達到條件，收斂速度較快，側面說明了本文算法的高效性。

4 結束語

本文提出一種基于相似圖投影學習的多視圖聚類（MSCGP）算法。首先該算法充分考慮了局部相似性，能夠自適應地學習樣本間的相似圖構造；充分借助自適應學習的投影圖，將共識圖和不同視圖的相似圖更好地融合，在統一的優化框架下聯合學習自適應圖、學習投影圖和共識圖；最后，通過直接動態融合得到最佳共識圖矩陣和譜嵌入矩陣，以及最后的聚類結構。通過實驗，在涉及到7個真實數據集的評估中，本文算法在11個對比算法中共涉及的21個聚類指標中表現出優異的結果。具體而言，本文算法在這些指標中有17個聚類指標排名最高，并且還有2個聚類指標排名次高，本文算法展現出了比對比算法更為穩定的整體聚類效果。經過對人工數據集和真實數據集的實驗，MCSGP算法證明了其有效性和出色的性能表現，但是本文算法的計算復雜度較高，導致運算時間較長。未來的研究將致力于在不大幅度降低算法精確度的前提下，進一步提升算法的運算效率。

參考文獻：

[1]Nigam K， Ghani R. Analyzing the effectiveness and applicability of co-training［C］//Proc of the 9th International Conference on Information and Knowledge Management.New York：ACM Press，2000：86-93.

［2]Cai Xiao， Nie Feiping， Huang Heng， et al. Heterogeneous image feature integration via multi-modal spectral clustering［C］//Proc of IEEE Conference on Computer Vision and Pattern Recognition.Washington DC：IEEE Computer Society，2011：1977-1984.

［3]Assent I， Domeniconi C， Gullo F， et al. MultiClust 2013： multiple clusterings， multiview data， and multisource knowledgedriven clustering［J］.ACM SIGKDD Explorations Newsletter，2016，18（1）：35-38.

［4]Xu Linli， Neufeld J， Larson B， et al. Maximum margin clustering［C］//Proc of the 17th International Conference on Neural Information Processing Systems.Cambridge，MA：MIT Press，2004：1537-1544.

［5]Zhao Bin， Kwok J T， Zhang Changshui. Multiple kernel clustering［C］//Proc of SIAM International Conference on Data Mining.［S.l.］：Society for Industrial and Applied Mathematics，2009：638-649.

［6]De Sa V R， Gallagher P W， Lewis J M， et al. Multi-view kernel construction［J］.Machine Learning，2010，79（1-2）：47-71.

［7]Yu Shi， Tranchevent L， Liu Xinhai， et al. Optimized data fusion for kernel K-means clustering［J］.IEEE Trans on Pattern Analysis and Machine Intelligence，2011，34（5）：1031-1039.

［8]Zhang Changqing， Fu Huazhu， Liu Si， et al. Low-rank tensor constrained multiview subspace clustering［C］//Proc of IEEE International Conference on Computer Vision.Washington DC：IEEE Compu-ter Society，2015：1582-1590.

［9]張華偉，陸新東，朱小明，等.基于t-SVD的結構保持多視圖子空間聚類［J］.計算機科學，2022，49（S2）：525-530.（Zhang Huawei， Lu Xindong， Zhu Xiaoming， et al. Structure preserved multi-view subspace clustering based on t-SVD［J］.Computer Science，2022，49（S2）：525-530.）

［10]Liu Xiaolan， Pan Gan， Xie Mengying. Multi-view subspace clustering with adaptive locally consistent graph regularization［J］.Neural Computing and Applications，2021，33（11）：15397-15412.

［11]洪振寧，蘇雅茹.非凸張量多視圖子空間聚類［J］.福州大學學報：自然科學版，2022，50（6）：737-741.（Hong Zhenning， Su Yaru. Non convex tensor multi-view subspace clustering［J］.Journal of Fuzhou University：Natural Science Edition，2022，50（6）：737-741.）

［12]Xu Chang， Tao Dacheng， Xu Chao. Multi-view self-paced learning for clustering［C］//Proc of the 24th International Conference on Artificial Intelligence.Palo Alto，CA：AAAI Press，2015：3974-3980.

［13]宋菲.基于聚類結構和局部相似性的多視圖隱空間聚類［J］.計算機應用研究，2023，40（9）：2650-2656.（Song Fei. Multi-view latent subspace clustering with cluster structure and local similarity［J］.Application Research of Computers，2023，40（9）：2650-2656.）

［14]Hussain S F， Mushtaq M， Halim Z. Multi-view document clustering via ensemble method［J］.Journal of Intelligent Information Systems，2014，43（1）：81-99.

［15]Serra A， Greco D， Tagliaferri R. Impact of different metrics on multi-view clustering［C］//Proc of International Joint Conference on Neural Networks.Piscataway，NJ：IEEE Press，2015：1-8.

［16]Xue Zhe， Li Guorong， Wang Shuhui， et al. GOMES：a group-aware multi-view fusion approach towards real-world image clustering［C］//Proc of IEEE International Conference on Multimedia and Expo.Piscataway，NJ：IEEE Press，2015：1-6.

［17]Hou Chenping， Nie Feiping， Tao Hong， et al. Multi-view unsupervised feature selection with adaptive similarity and view weight［J］.IEEE Trans on Knowledge and Data Engineering，2017，29（9）：1998-2011.

［18]Nie Feiping， Wang Xiaoqian， Huang Heng. Clustering and projected clustering with adaptive neighbors［C］//Proc of the 20th ACM SIGKDD international Conference on Knowledge Discovery and Data Mining.New York：ACM Press，2014：977-986.

［19]Zhan Kun， Zhang Chanqing， Guan Junpeng， et al. Graph learning for multiview clustering［J］.IEEE Trans on Cybernetics，2017，48（10）：2887-2895.

［20]Wang Hao， Yang Yan， Liu Bing. GMC：graph-based multi-view clustering［J］.IEEE Trans on Knowledge and Data Engineering，2019，32（6）：1116-1129.

［21]Nie Feiping， Cai Guohao， Li Xuelong. Multi-view clustering and semi-supervised classification with adaptive neighbours［C］//Proc of the 31st AAAI Conference on Artificial Intelligence.Palo Alto，CA：AAAI Press，2017：2408-2414.

［22]Nie Feiping， Zhang Rui， Li Xuelong. A generalized power iteration method for solving quadratic problem on the Stiefel manifold［J］.Science China Information Sciences，2017，60（5）：article No.112101.

［23]Fiori S. Formulation and integration of learning differential equations on the Stiefel manifold［J］.IEEE Trans on Neural Networks，2005，16（6）：1697-1701.

［24]Liu Jialu， Wang Chi， Gao Jing， et al. Multi-view clustering via joint nonnegative matrix factorization［C］//Proc of SIAM International Conference on Data Mining.［S.l.］：Society for Industrial and Applied Mathematics，2013：252-260.

［25]Huang H C， Chuang Y Y， Chen Chusong. Affinity aggregation for spectral clustering［C］//Proc of IEEE Conference on Computer Vision and Pattern Recognition.Washington DC：IEEE Computer Society，2012：773-780.

［26]Nie Feiping， Tian Lai， Li Xuelong. Multiview clustering via adaptively weighted Procrustes［C］//Proc of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining.New York：ACM Press，2018：2022-2030.

［27]Kumar A， Rai P， Daume H. Co-regularized multi-view spectral clustering［C］//Proc of the 24th International Conference on Neural Information Processing Systems.Red Hook，NY：Curran Associates Inc.，2011：1413-1421.

［28]Zhan Kun， Nie Feiping， Wang Jing， et al. Multiview consensus graph clustering［J］.IEEE Trans on Image Processing，2019，28（3）：1261-1270.

［29]Luong K， Nayak R， Balasubramaniam T， et al. Multi-layer manifold learning for deep non-negative matrix factorization-based multi-view clustering［J］.Pattern Recognition，2022，131（11）：108815.

［30]Xia Rongkai， Pan Yan， Du Lei， et al. Robust multi-view spectral clustering via low-rank and sparse decomposition［C］//Proc of the 28th AAAI Conference on Artificial Intelligence.Palo Alto，CA：AAAI Press，2014：2149-2155.

［31]Huang Dong， Wang Changdong， Lai Jianhuang. Fast multi-view clustering via ensembles：towards scalability， superiority， and simplicity［J］.IEEE Trans on Knowledge and Data Engineering，2023，35（11）：11388-11402.