一種多線程概念約簡算法

祁斌,祁建軍,2,李俊安,趙思雨,折延宏

(1. 西安電子科技大學計算機科學與技術學院,710071,西安; 2. 新疆政法學院信息網絡安全學院,844000,新疆圖木舒克; 3. 咸陽師范學院數學與統計學院,712000,陜西咸陽;4. 西安石油大學理學院,710065,西安)

德國數學家Wille于20世紀八十年代為重構格理論提出了形式概念分析(formal concept analysis,FCA)[1-2]。該理論自提出至今得到了很大的發展,已經突破了格論自身,被廣泛應用到諸如數據挖掘[3-4]、軟件工程[5-6]、知識工程[7-8]、推薦系統[9-10]和信息檢索[11-12]等領域,成為解決知識發現問題的重要理論和工具之一。

概念約簡是形式概念分析理論的一個新的研究方向,由魏玲等[13-14]于2018年提出。概念約簡的目標是獲取保持二元關系不變的極小概念集,這樣可以在完全不損失形式背景原始信息的情況下,減少概念數量,降低使用形式概念分析解決問題的復雜性。目前,概念約簡算法相對較少,魏玲等[14]在2020年提出了基于二元關系的概念約簡算法。Zhao等[15]在文獻[14]的基礎上進一步研究,提出代表概念矩陣的定義,簡明直觀地展示了二元關系與概念之間的聯系,并給出了基于代表概念矩陣的串行概念約簡算法(serial concept reduction,SCR)。謝小賢等[16]從布爾運算的角度研究了保持二元關系不變的概念約簡。馬文勝等[17]針對計算部分概念約簡的問題,提出同效關系,并給出通過同效關系求解概念約簡的方法。李俊余等[18]提出三元概念約簡,可保持三元背景中所有的三元關系不變。王霞等[19]提出一種基于概念可辨識矩陣對概念類別進行判定的方法。劉津等[20]提出了基于概念可辨識矩陣的對偶三支概念約簡方法。

SCR算法將概念通過對象和屬性分別聚類的方式構建代表概念矩陣,并使用代表概念矩陣計算概念約簡,其時間復雜度低于文獻[14]和文獻[16]中概念約簡算法的時間復雜度,較二者具有更快的執行速度,但SCR算法中并沒有使用多線程方法,執行效率仍然不高。針對此問題,提出一種多線程概念約簡算法(multi-thread concept reduction, MTCR)。MTCR算法使用構建代表概念矩陣的思想,通過兩個線程分別對對象集和屬性集單獨處理,計算每個對象的對象代表概念集和每個屬性的屬性代表概念集,并以多線程并行計算方式獲取任意對象的對象代表概念集和任意屬性的屬性代表概念集中共有概念,從而構建出代表概念矩陣。本文是在多核環境下運行多線程程序,通過使用多線程,提高概念約簡算法的執行效率。

1 概念約簡基礎理論

先給出形式概念分析的基礎知識。

定義1[1]稱(G,M,I)為一個形式背景,其中G={g1,…,gp}為對象集,每個gi(i≤p)稱為一個對象;M={m1,…,mq}為屬性集,每個mj(j≤q)稱為一個屬性;I為G和M之間的二元關系,即I?G×M。若(g,m)∈I,則表示對象g具有屬性m,也記為gIm。

例1:表1是一個形式背景(G,M,I),其對象集G={1,2,3,4,5},屬性集M={a,b,c,d,e}。表中將(g,m)∈I記為1,(g,m)?I記為0。

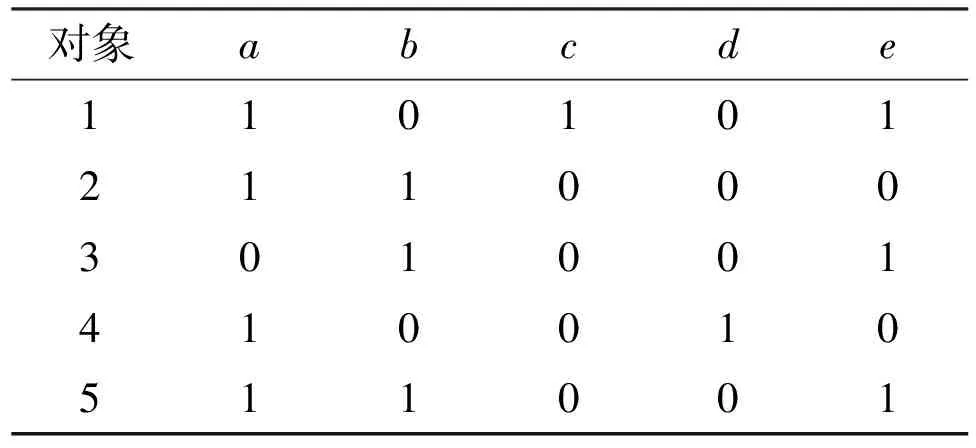
表1 一個形式背景(G, M, I)

對于形式背景(G,M,I),在對象子集X?G和屬性子集B?M上可以定義一對對偶算子

X*={m|m∈M,?g∈X,gIm}

B*={g|g∈G,?m∈B,gIm}

其中X*表示X中所有對象共同具有的屬性集合,B*表示共同具有B中所有屬性的對象集合。

對于任意的X?G,B?M,若X*=B且B*=X,則稱(X,B)為形式概念,簡稱概念。其中X稱為概念的外延,B稱為概念的內涵。

將形式背景(G,M,I)所有形式概念的集合記為L(G,M,I)。對于任意的(X1,B1),(X2,B2)∈L(G,M,I),定義如下的偏序關系

(X1,B1)≤ (X2,B2)?X1?X2(B1?B2)

任意兩個概念的下確界、上確界為

(X1,B1)∧(X2,B2)=(X1∩X2, (B1∪B2)**)

(X1,B1)∨(X2,B2)=((X1∪X2)**,B1∩B2)

從而L(G,M,I)形成一個完備格,被稱為概念格。

例2:例1中形式背景構建的概念格如圖1所示。為了使用方便,本文中所有概念的外延、內涵都以羅列其中元素的序列形式給出,并對所有概念進行編號。

圖1 L(G,M,I)Fig.1 L(G,M,I)

概念格雖然可以清晰地展示形式背景中概念之間的層次關系,但是在知識還原方面,概念格中的概念信息存在冗余,而通過概念約簡僅用部分概念就可以完全還原形式背景的全部信息。下面給出概念約簡的相關定義。

定義2[14]設(G,M,I)是一個形式背景,L(G,M,I)是概念格,F?L(G,M,I)。如果I=∪(X,B)∈F(X×B),則稱F為保持二元關系I不變的概念協調集;若對任意的(Xi,Bi)∈F,F′=F{(Xi,Bi)},有I≠∪(X,B)∈F′(X×B),則稱F為保持二元關系I不變的概念約簡。

注由文獻[15]可知,概念格中頂元與底元均不存在于概念約簡中。因此,這兩種概念在之后的討論中不予考慮。

定義3[15]設(G,M,I)為形式背景,gi∈G,mj∈M。如果存在(X,B)∈L(G,M,I),滿足gi∈X且mj∈B,那么稱(X,B)為(gi,mj)的一個代表概念。記REP((gi,mj))={(X,B)∈L(G,M,I)|(gi,mj)∈X×B},稱REP((gi,mj))為(gi,mj)的代表概念集;記Λ=(REP((gi,mj)),gi∈G,mj∈M)|G|×|M|為代表概念集REP((gi,mj))構成的矩陣,稱Λ為(G,M,I)的代表概念矩陣。

定義4設(G,M,I)為形式背景,gi∈G,mj∈M。如果存在(X,B)∈L(G,M,I),滿足gi∈X,那么稱(X,B)為對象gi的對象代表概念,記REP(gi)={(X,B)∈L(G,M,I)|gi∈X},稱REP(gi)為對象gi的對象代表概念集;若存在(X,B)∈L(G,M,I),滿足mj∈B,那么稱(X,B)為屬性mj的屬性代表概念,記REP(mj)={(X,B)∈L(G,M,I)|mj∈B},稱REP(mj)為屬性mj的屬性代表概念集。

根據對象gi的對象代表概念集和屬性mj的屬性代表概念集的定義,可以得到如下性質。

性質1設(G,M,I)為形式背景,gi∈G,mj∈M,則有REP((gi,mj))=REP(gi)∩REP(mj)。

例3:L(G,M,I)中每一個對象的對象代表概念集和每一個屬性的屬性代表概念集分別如表2和表3所示。

表2 例1中的REP(gi)

表3 例1中的REP(mj)

例1中代表概念矩陣Λ如下所示。

矩陣共有5行5列。第i行第j列的代表概念集表示外延包含第i個對象gi,同時內涵包含第j個屬性mj的所有代表概念。代表概念由對象gi的對象代表概念集REP(gi)和屬性mj的屬性代表概念集REP(mj)做交運算獲得。例如代表概念矩陣第1行第1列的概念集合由對象1的對象代表概念集{c2,c3,c6,c9}和屬性a的屬性代表概念集{c2,c5,c6,c8,c9,c10}做交運算獲得,即滿足外延包含對象1同時內涵包含屬性a的所有概念為{c2,c6,c9}。空集?表示不存在相應的代表概念。

為了得到概念約簡,可以將代表概念矩陣中的代表概念集羅列,并在每個代表概念集中任取一個概念進行組合,得到概念協調集,其中極小的集合就是概念約簡。具體方法由命題1給出。

命題1[15]設(G,M,I)為形式背景,L(G,M,I)是其概念格,對任意的(gi,mj)∈I,記代表概念函數f(Λ)=ΛREP((gi,mj))∈Λ(∨(X,B)∈REP((gi,mj))(X,B)),則f(Λ)所對應的極小析取范式中的所有合取式為該形式背景所對應的概念約簡全體。

在代表概念矩陣中可以很明顯發現,代表概念集之間可能存在包含關系。這種包含關系使代表概念矩陣中存在大量重復信息,造成信息冗余。為了降低概念約簡的計算復雜度,提升概念約簡執行效率,可以通過刪除包含元素,保留被包含元素的方式,將代表概念矩陣簡化。簡化后的代表概念矩陣稱為最小代表概念矩陣。上面的代表概念矩陣簡化結果如下

Λmin=

由例3中最小代表概念矩陣Λmin,可以得到4個概念約簡結果為{c5,c7,c8,c9}、{c2,c4,c5,c7,c9}、{c2,c3,c4,c5,c9}和{c3,c4,c5,c8,c9}。

2 MTCR概念約簡算法

2.1 SCR概念約簡算法

圖2為使用SCR算法計算概念約簡的流程圖,主要包含4個步驟。

(1)計算概念:將輸入的形式背景通過概念格構建算法計算生成所有形式概念。

(2)計算代表概念矩陣:計算所有對象的對象代表概念集和所有屬性的屬性代表概念集,并通過任意對象的對象代表概念集和任意屬性的屬性代表概念集中的共有概念構建代表概念矩陣。

(3)計算最小代表概念矩陣:判斷代表概念矩陣中代表概念集之間的包含關系。若兩個不同的代表概念集之間存在包含關系,則刪除包含的代表概念集,保留被包含的代表概念集。若代表概念矩陣中任意兩個代表概念集之間均不存在包含關系,則該矩陣為最小代表概念矩陣。

(4)計算概念約簡結果:計算最小代表概念矩陣中所有非空代表概念集極小析取范式中的所有合取式獲得概念約簡。

在上述4個步驟中,因為第1步和第4步的算法已相對成熟[21-25],所以在概念約簡中使用現有算法,SCR算法只提出第2步和第3步的算法。第2步是SCR算法的核心步驟,也是占用時間最長的步驟,因此MTCR概念約簡算法對第2步實現多線程并行計算方式改進,其余步驟與SCR算法保持一致。

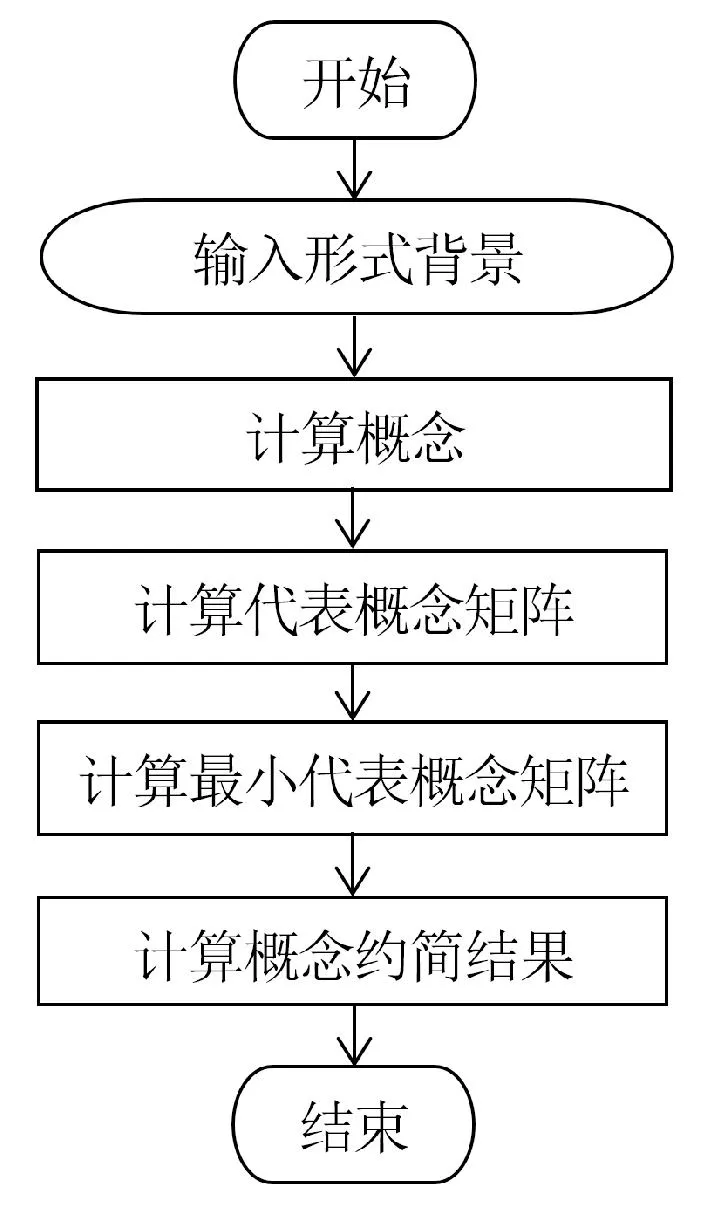
圖2 概念約簡計算過程流程圖Fig.2 The flow chart of concept reduct calculation

2.2 MTCR概念約簡算法

計算代表概念矩陣分為兩步,先計算對象代表概念集REP(gi)和屬性代表概念集REP(mj),再計算REP(gi)和REP(mj)中的共有概念。

MTCR算法在計算代表概念矩陣時,先以對象和屬性為出發點,通過不同線程并行計算每一個對象gi的對象代表概念集REP(gi)和每一個屬性mj的屬性代表概念集REP(mj)。實現過程如算法1所示。

算法1:計算對象代表概念集和屬性代表概念集。輸入概念集合concepts,輸出為對象代表概念集objs[i]和屬性代表概念集attrs[j]。

1 Process1:

2 fori= 0 to |G|

3 for (X,B) in concepts

4 ifgi∈X

5 Add (X,B) to objs[i];

6 end if

7 end for

8 end for

9 Process2:

10 forj=0 to |M|

11 for (X,B) in concepts

12 ifmj∈B

13 Add (X,B) to attrs[j];

14 end if

15 end for

16end for

算法1創建了線程1、線程2,兩個線程并行執行。算法第1行到第8行,創建線程1并計算每一個對象的對象代表概念集。遍歷L(G,M,I)中的概念,將外延中包含對象gi的所有概念的標志以位運算的方式存于objs[i]中。

算法第9行到第16行,創建線程2并計算每一個屬性的屬性代表概念集。遍歷L(G,M,I)中的概念,將內涵中包含屬性mj的所有概念的標志以位運算的方式存于attrs[j]中。

通過對象代表概念集REP(gi)和屬性代表概念集REP(mj)可以計算出(gi,mj)的代表概念集。在計算過程中,每計算一個代表概念集,都會查詢相應的對象代表概念集和屬性代表概念集,但不同代表概念集的計算過程互不影響。因此為了提高計算效率,可以使用多線程方式并行計算不同代表概念集。將形式背景中的對象依次放入p個隊列,并為每個隊列分配線程,通過多線程方式并行計算出任意對象的對象代表概念集和任意屬性的屬性代表概念集的交集,最終得到代表概念矩陣。實現過程如算法2所示。

算法2:計算代表概念矩陣。輸入對象代表概念集objs[i]和屬性代表概念集attrs[j],輸出代表概念矩陣represented[i][j]。

1 for obj in context

2 count ++;

3 Store(obj, queue[count%p]);

4 end for

5 forq=0 top-1

6 new process;

7 for obj in queue[q]

8i←obj;

9 forj=0 to |M|

10 if objs[i]∩attrs[j] ≠ ?

11 represented[i][j]= objs[i]∩attrs[j];

12 end if

13 end for

14 end for

15end for

算法第1行到第4行,將形式背景中的對象依次存入p個隊列。

算法第5行到第15行,為每個隊列分配線程,分別計算隊列中所含對象的對象代表概念集和與每一個屬性的屬性代表概念集中的共有概念。由性質1可知,結果即為外延具有特定對象且內涵具有特定屬性的概念集合,并將其存于代表概念矩陣represented中。

算法2以形式背景中對象為分配數據依次放入p個隊列,計算任意對象的對象代表概念集與任意屬性的屬性代表概念集中的共有概念構建代表概念矩陣。若將算法2中的對象與屬性互換,以屬性作為分配數據放入p個隊列,同樣可以得到代表概念矩陣,并且與算法2計算得到的代表概念矩陣一致。為了使多線程負載均衡,當形式背景中對象數大于等于屬性數時,MTCR算法使用以對象為分配數據的方式進行計算;當形式背景中的對象數小于屬性數時,MTCR算法以屬性為分配數據的方式進行計算。

通過多線程并行計算對象代表概念集和屬性代表概念集的方法計算代表概念矩陣,極大地提高了執行效率。

3 實驗結果與分析

實驗在Apple M1 Pro 10核、主頻為3.20 GHz、內存為16 GB的便攜式計算機上進行,分別對例1中形式背景和4種UCI數據集進行處理,分析SCR算法與MTCR算法在性能上的區別,表明MTCR算法可以準確得到概念約簡結果,并且在運行速度上快于SCR算法。在對比實驗2中使用隨機數據集,分別考慮屬性數量、對象數量和密度大小對MTCR算法性能的影響。

實驗中計算概念步驟和計算概念約簡結果步驟分別使用Andrews[24]提出的InClose3算法和智慧來等[25]提出的極小覆蓋法。為了直觀對比MTCR算法相對于SCR算法在執行速度上的提升,我們僅比較計算代表概念矩陣和計算最小代表概念矩陣消耗的總時間,并計算提升效率。

例1中使用MTCR算法的實驗結果如表4所示,其中t為計算概念約簡所需時間。表4中概念約簡結果與例3中計算得到的概念約簡結果相同,表明MTCR算法的準確性。

對比實驗1使用的UCI數據集是UCI Machine Learning Repository網站中提供的Balance-Scale、Car、Iris和Wine這4個數據集,對比SCR算法和MTCR算法在執行時間上的差異,對比結果如表5所示,MTCR運行時間為使用兩個線程時所消耗的時間。SCR算法分別與1、2、4和8個線程的MTCR算法對比結果如圖3所示。

通過對4個UCI數據集進行實驗,由圖3可以明確觀察到使用MTCR概念約簡算法在計算概念約簡時,使用單線程情況下,與SCR算法計算時間幾乎相同;使用2、4和8線程時,MTCR算法使用時間均少于SCR算法。當線程數不超過8時,線程數每增加1倍,計算速度可以提高約30%。

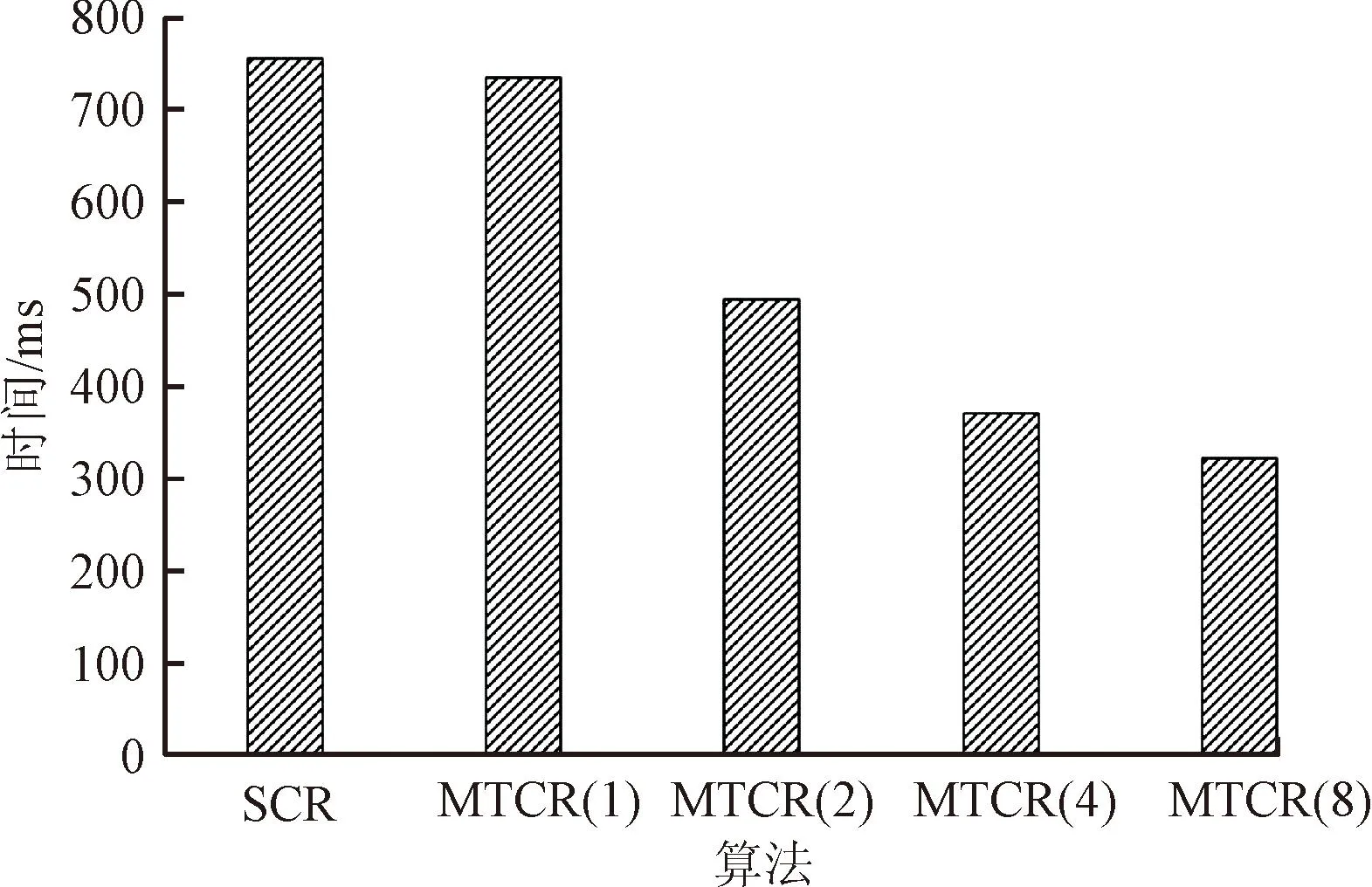
(a)Balance-Scale

(b)Car

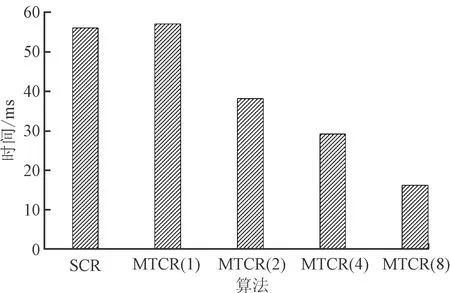
(c)Iris

(d)Wine

表4 例1實驗運行過程表

表5 4個UCI數據集實驗結果

對比實驗2,為了進一步驗證MTCR算法的高效性,對隨機數據進行實驗,固定形式背景中其他變量,分別改變屬性數量,對象數量和密度大小,分析對不同數量線程性能的影響,實驗結果如圖4所示。

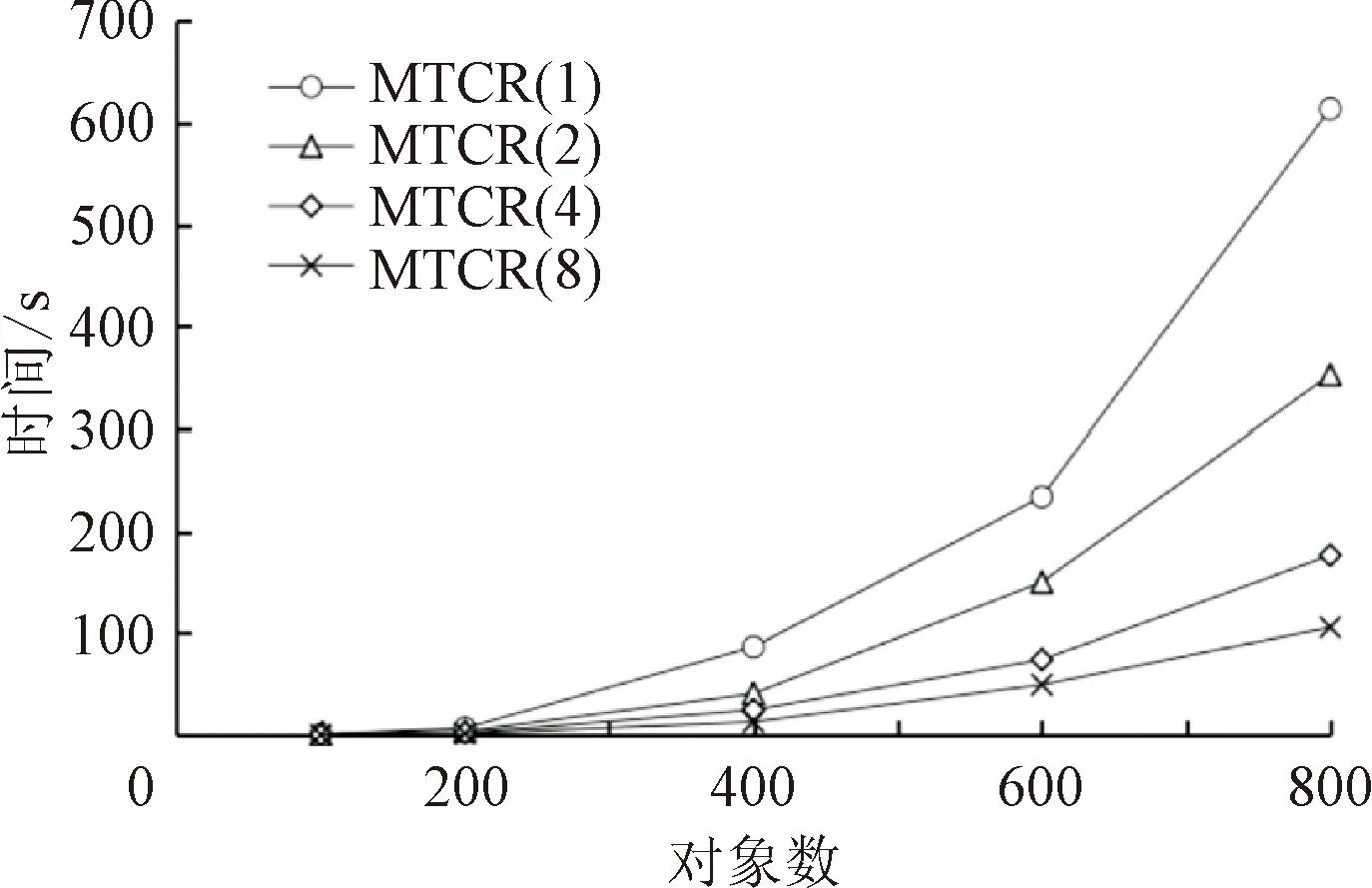
(a)對象數(|M|=30,d=30%)

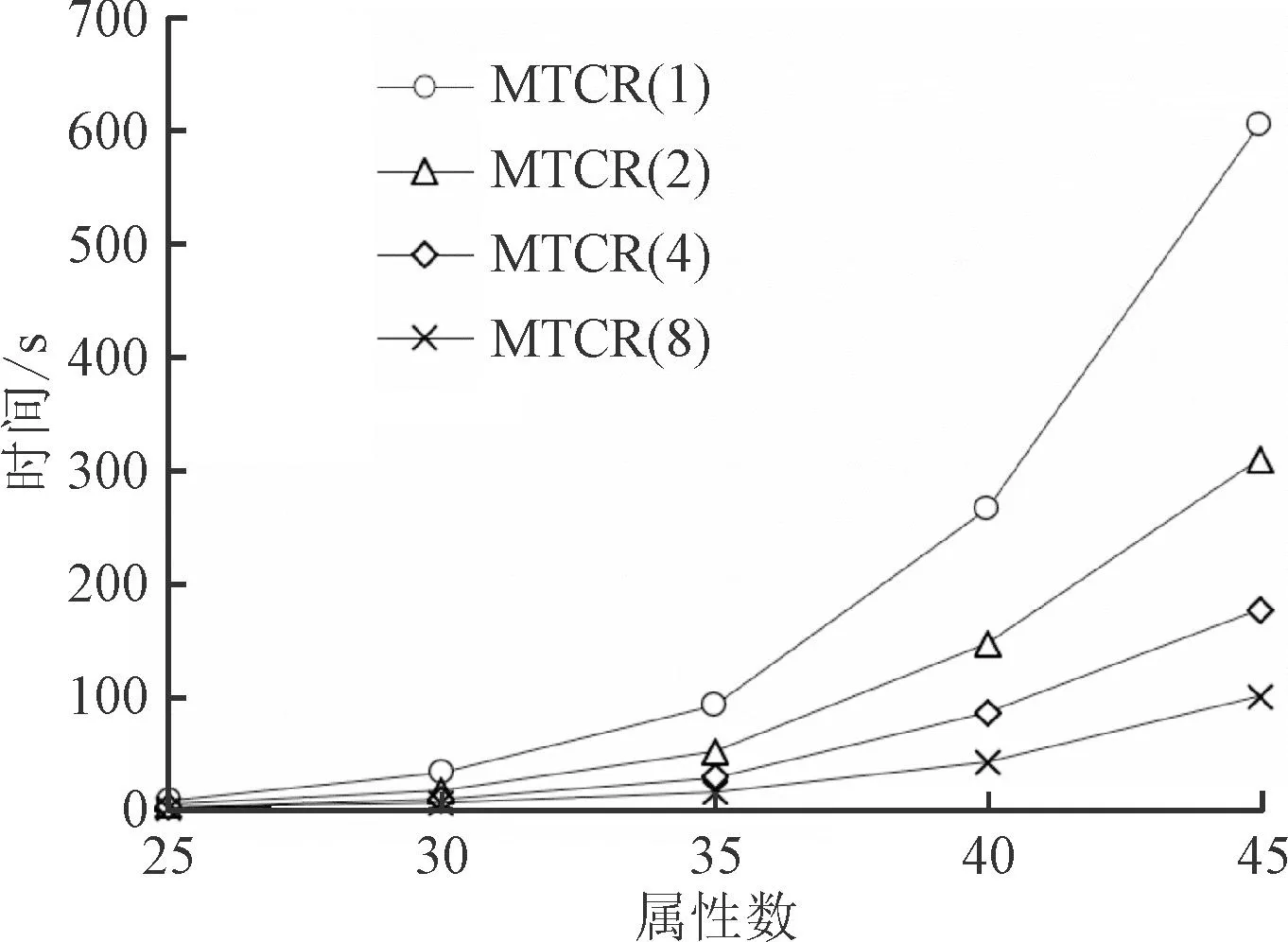
(b)屬性數(|G|=300,d=30%)

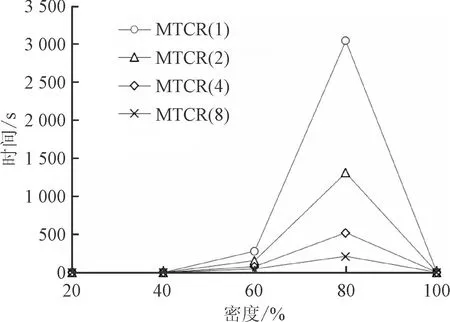
(c)密度(|G|=100,|M|=20)

圖4(a)為固定形式背景的屬性數量為30,密度為30%,對象數量的變化范圍為100～800;圖4(b)為固定形式背景的對象數量為300,密度為30%,屬性數量的變化范圍為25～45;圖4 (c)為固定形式背景對象數為100,屬性數為20,密度大小的變化范圍為20%～100%。

在形式概念分析中,對象與屬性呈對偶關系,對象數與屬性數對MTCR算法的性能具有相同的影響。由圖4中(a)、(b)可知,固定其他變量,僅改變對象數(屬性數)時,MTCR算法計算時間隨對象數(屬性數)增加而增加,當對象數和屬性數都較大時,形式背景中的概念數量呈指數倍增長,MTCR算法計算時間也呈指數倍增長。由圖4(c)可知,固定對象數和屬性數不變,形式背景密度處于80%左右時,概念數量相對較多,MTCR算法計算時間較長,密度趨于0%和100%時,概念數量相對較少,MTCR算法計算時間較短。

通過對UCI數據集和隨機數據集的實驗分析可知,MTCR算法使用的線程數量增長對算法效率的提升趨于穩定,當線程數不超過8時,隨著線程數量每增加1倍,MTCR算法計算效率均可提速30%以上。但是,隨著概念數量的增長,MTCR算法在使用固定數量的多線程情況下,計算所需時間隨概念數量的增長呈指數倍增長。在處理較大規模的數據集時,應增加線程數量,以提高計算效率。

4 結束語

本文基于通過構建代表概念矩陣計算概念約簡的方法,對SCR算法中計算過程復雜,執行效率低的部分提出并行化處理方案。通過對例1中的形式背景、UCI數據集和隨機數據集的實驗表明,MTCR算法能準確、快速地計算出概念約簡的結果,極大提高概念約簡算法的執行效率。當線程數不超過8時,隨著線程數量每增加1倍,MTCR算法計算效率均可以提升30%以上。