基于兩級濾波的改進滑模觀測器PMSM無速度傳感器控制

劉紅俐,黃 旭,朱其新,2,朱永紅

(1.蘇州科技大學 機械工程學院,江蘇 蘇州 215009;2.蘇州市共融機器人技術重點實驗室,江蘇 蘇州 215009;3.景德鎮(zhèn)陶瓷大學 機電工程學院,江西 景德鎮(zhèn) 333001 )

0 引 言

PMSM因其體積小、質量輕、效率高等優(yōu)點在交流伺服領域得到了廣泛應用[1-2]。因為PMSM系統(tǒng)中轉子位置和速度信號非常重要,但是傳統(tǒng)的機械傳感器易受溫度、磁場以及其他外部干擾的影響,越來越不能滿足系統(tǒng)準確性的要求,所以無位置傳感器控制開始出現(xiàn)[3-7]。

無位置傳感器控制方法主要包含2類：一類是適用于低速的高頻信號注入法,包括旋轉高頻電壓信號法和脈沖高頻電壓信號法;還有一類是適用于高速的基于電機基頻模型法,包括定子磁鏈估算法、模型參考自適應法 、狀態(tài)觀測器估算法 、人工智能估算法等。滑模觀測器屬于狀態(tài)觀測器的一種,通過輸入的電壓電流估算出反電動勢,然后由反電動勢估計出定子的位置和轉速信息。它的優(yōu)點在于結構簡單、不依賴系統(tǒng)精確的數(shù)學模型、不受內部參數(shù)和外部干擾的影響、魯棒性強。缺點是滑模控制導致的抖振難以消除。而且滑模觀測器本身就不能解決不同轉速條件下轉子位置估計的問題。文獻[8]運用高頻反電動勢觀測器解決了高頻信號的濾波;文獻[9]從滑模控制率出發(fā)提出非奇異新型快速終端滑模控制以提高系統(tǒng)的準確性,但沒有考慮外部擾動誤差,應用條件有限;文獻[10]利用鎖相環(huán)技術提高了位置追蹤的性能,但補償精度不夠,觀測超調過大;文獻[11]提出的二次濾波方法,通過使用變截止頻率提高了在反電動勢高頻分量變化時的自適應能力,但因為轉子位置需要過多補償,增加了計算難度;文獻[12-13]提出卡爾曼濾波和滑模觀測器結合的方法,抑制了抖振,減小了高頻噪聲,但對于角位置的延遲沒有進行補償。滑模觀測器魯棒性強,不依賴系統(tǒng)精確模型[14-15],卡爾曼濾波算法利用含有噪聲的線性傳感器數(shù)據(jù)使線性隨機系統(tǒng)的均方估計誤差最小化[16],能過濾高頻噪聲但對模型精度要求較高[17],兩者可以相互補充形成復合控制器更好實現(xiàn)伺服系統(tǒng)的精準快速控制。

基于以上討論,提出了一種基于兩極濾波的PMSM改進滑模觀測器。針對PMSM高速低速不同狀態(tài)轉子估計的精度問題,提出了兩級濾波的方法,進行自適應低通濾波以及兩級卡爾曼濾波。針對滑模觀測器抖振的問題,提出了改進滑模控制律。最后與傳統(tǒng)觀測器進行了仿真對比,驗證了所提方法的優(yōu)越性。

1 三相PMSM數(shù)學模型

假設永磁同步電動機處于理想狀態(tài),并做出以下假設[18-19]

1) 永磁體的磁動勢是固定的;

2) 電機的反電動勢是正弦的;

3) 電機轉子上沒有阻尼繞組;

4) 電機的感應電動勢和氣隙磁場是正弦的,不考慮磁場的所有諧波;

5) 三相定子繞組在定子空間中對稱分布,三相繞組中的電樞電阻相等,三相繞組中的電感也相等;

6) 不考慮電機鐵芯的永磁飽和和電機中的渦流損耗;

7) 不考慮電機周圍環(huán)境溫度對電機的影響。

選取在d-q坐標系下進行研究,在d-q坐標系下PMSM的模型為[19]：

(1)

λq=Lqiq

(2)

λd=Ldid+Lmdidf

(3)

ωe=pnωr

(4)

式中：id、iq分別為定子電流d、q軸分量;Ud、Uq分別為定子電壓d、q軸分量;rs為定子電阻;Ld、Lq分別為定子d、q軸電感;ωe為轉子電角速度;ωr為轉子機械角速度;λd、λq為d、q軸定子磁鏈;Lmd為d軸的互感;idf為d軸等效磁化電流;pn為極對數(shù)。

PMSM電磁轉矩和機械運動方程為

Te=3pn[Lmdidfiq+(Ld-Lq)idiq]/2

(5)

(6)

式中：Te為電磁轉矩;TL為負載轉矩;B為摩擦因數(shù);J為轉動慣量。

由于B一般很小,又有

(7)

在表貼式PMSM中,由于Ld=Lq,此時電機的電磁轉矩方程可簡化為

Te=3pnLmdidfiq/2

(8)

PMSM在α-β靜止坐標系下的數(shù)學模型[20-21]如下所示。

電壓方程為

(9)

式中：iα、iβ和uα、uβ分別是α-β坐標系下的定子電流和定子電壓;φα、φβ為α-β坐標系下的磁鏈。

磁鏈方程為

(10)

(11)

式中：ψf為永磁體磁鏈;Eα、Eβ為α-β坐標系下的反電動勢;θ為轉子位置電角度。

轉矩方程為

Te=1.5pn(φαiβ-φβiα)

(12)

2 改進滑模觀測器設計

2.1 傳統(tǒng)滑模觀測器

滑模觀測器由滑模控制發(fā)展而來,其繼承了滑模變結構控制的優(yōu)點,其結構原理如圖1所示。

圖 1 滑模觀測器原理圖Fig.1 Schematic diagram of sliding mode observer

由式(9)、(10)、(11)可以得到

(13)

式中：Ls為定子繞組電感。

滑模觀測器根據(jù)基準電流和反饋電流的誤差來構建數(shù)學模型

(14)

將式(13)和(14)相減可得

(15)

當滑模進入到達階段即在滑模面上運動時

(16)

綜上,傳統(tǒng)滑模觀測器存在以下問題[22-26]：

1) 傳統(tǒng)的滑模觀測器使用sgn函數(shù)作為切換函數(shù)。sgn函數(shù)是一個不連續(xù)的階躍函數(shù),當系統(tǒng)進行高頻切換時,會發(fā)生嚴重的系統(tǒng)抖振,極大降低了控制系統(tǒng)的精度和穩(wěn)定性。

2) 在傳統(tǒng)的滑模觀測器中,低通濾波器用于濾除反電勢信號中的高頻諧波。由于低通濾波器的使用會引起控制系統(tǒng)的延遲問題,這種延遲現(xiàn)象在高速電機控制系統(tǒng)中尤為明顯。此外,相位延遲的存在要求控制系統(tǒng)對延遲進行補償,這使得系統(tǒng)中的計算量很大,增加了系統(tǒng)負擔,降低了系統(tǒng)響應速度,影響了控制系統(tǒng)的跟隨性能。

3) 傳統(tǒng)的滑模觀測器采用反正切函數(shù)來計算轉子的速度和位置,此方法存在較大誤差。

2.2 改進滑模觀測器

滑模觀測器的趨近律決定了觀測器抑制抖振的能力。符號函數(shù)存在切換過程不連續(xù)的問題,容易引起系統(tǒng)的不穩(wěn)定。而趨近律的切換增益的大小既決定了趨近速度,也決定了到達階段后抖振的大小。針對這2個問題提出滑模面S的新型趨近律：

(17)

式中：當|S|大于邊界層厚度a時,sat(S)=sgn(S); 當|S|不大于邊界層厚度a時,sat(S)=sgn(S)S2/a2;切換增益ε=kωref,ωref為給定轉速,k為可變增益。

新的飽和函數(shù)為連續(xù)函數(shù),并且恰當?shù)倪吔鐚雍穸瓤梢越档秃透纳普w的抖振,但會影響系統(tǒng)的精度。所以將切換增益ε引入轉速,并且通過可變增益k進行調節(jié)以達到自適應的效果。

根據(jù)李雅普諾夫穩(wěn)定性條件可得

(18)

由此可得,只要k>max(eα,eβ),即可滿足存在可達和穩(wěn)定的條件。

3 兩級濾波器設計

滑模觀測器觀測到的結果仍然存在大量高頻諧波分量和噪聲,會影響到轉子位置的估計,所以常常采用濾波器進行處理。諧波一般是當PMSM空載時,電機的轉子被外部的拖動電機帶動旋轉時,轉子的磁場切割定子線圈,根據(jù)法拉利電磁感應定律,線圈內變化的磁場產生電動勢,相上的電動勢,即每一相的空載反電動勢。由于 PMSM 齒槽效應、磁路飽和效應以及繞組的分布形式等因素引起的氣隙磁場畸變使得電機的三相電流中含有大量的空間諧波。普通的濾波器直接對輸入信號進行濾波,再經過轉子位置估計得到轉子位置和速度信息,如圖2所示。

圖 2 低通濾波器原理示意圖Fig.2 Schematic diagram of low-pass filter principle

低通濾波器傳遞函數(shù)為

H(s)=ωc/(s+ωc)

(19)

式中：ωc為截止頻率。

低通濾波器濾除高頻諧波后的擴張反電動勢為

(20)

低通濾波器的延遲會引入信號的相移效應,從而可能影響控制系統(tǒng)的響應速度和穩(wěn)定性。較大的延遲可能導致控制系統(tǒng)的相位裕度減小,進而影響系統(tǒng)的穩(wěn)定性。

由于電機運行過程中轉速會因為外部干擾而產生變化,所以高頻諧波分量也會發(fā)生變化。此時定值的截止頻率不能滿足系統(tǒng)的要求,因此用變截止頻率代替固定截止頻率的低通濾波器。所采用的截止頻率低通濾波器的截止頻率為

(21)

其濾除高頻諧波后的擴張反動勢為

(22)

雖然經過低通濾波器,但系統(tǒng)輸出仍然還有紋波分量。常見的反電動勢觀測器利用反正切函數(shù)估算轉子位置誤差仍然會過大,解決不了紋波分量的問題,所以采用卡爾曼濾波器進行兩級濾波。原理如圖3所示。

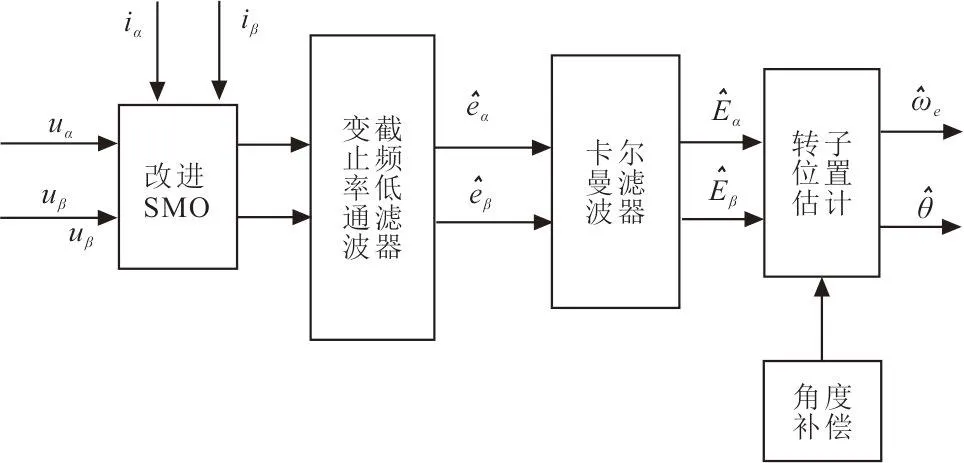
圖 3 兩級濾波器原理圖Fig.3 Schematic diagram of two-stage filter

卡爾曼濾波器狀態(tài)方程為

(23)

式中：M是卡爾曼濾波器增益,M的大小會影響響應速度以及系統(tǒng)的振動情況,所以選取適當?shù)膮?shù)有助于保障系統(tǒng)的穩(wěn)定。

兩級濾波后需要經過反正切函數(shù)的計算得到轉子角度信息

(24)

由于兩極濾波器的特性必然會使信號產生相位延遲,轉子位置必須進行角度補償。

(25)

將式(24)帶入式(10)可得最終角速度表達式為

(26)

4 系統(tǒng)仿真

4.1 仿真參數(shù)設置

為了驗證本文改進二階濾波的滑模觀測器控制算法的正確性,在Simulink中搭建PMSM仿真結構如圖4所示。

圖 4 PMSM仿真結構Fig.4 PMSM simulation structure

電機的具體參數(shù)：定子電阻rs=2.46 Ω;d、q軸電感Ld=Lq=6.35 mH;永磁磁鏈ψf=0.175 Wb;轉動慣量J=1.02 g·m2;體摩擦因數(shù)B=0.000 1;極對數(shù)pn=4;額定轉速3 000 r/min,逆變器開關頻率為15 kHz。

4.2 仿真結果的分析

給定電機轉速為1 000r/min,則PMSM滑模觀測器反電動勢仿真波形如圖5所示。

圖 5 改進前后滑模觀測器反電動勢對比Fig.5 Comparison of back electromotiveforce of sliding mode observer before and after improvement

從圖5可以看出,傳統(tǒng)滑模觀測器為陰影部分,新型觀測器為實線部分。陰影部分抖振較大、高頻分量較多,因此改進的二階濾波滑模觀測器觀測結果精度更高。

圖6表示2種觀測器在額定轉速下的轉速觀測誤差。

圖 6 2種觀測器在額定轉速的轉速觀測誤差Fig.6 Speed error of two observers at rated speed

從圖6可以看出,傳統(tǒng)觀測器轉速誤差在20 r/min,改進的二階濾波觀測器在10 r/min以內,其準確度更高。綜合轉速誤差和反電動勢觀測圖,可以看出,與傳統(tǒng)的觀測器相比,改進的觀測器使用了二級濾波減小了相位延遲對系統(tǒng)的影響,系統(tǒng)的轉速誤差也得到了很大的改善。

為了驗證本文提出的永磁交流伺服系統(tǒng)的抗干擾性能,在永磁交流伺服系統(tǒng)空載啟動0.5 s后增加10 N·m的負載轉矩,此時系統(tǒng)的轉速響應和電磁轉矩響應如圖7和圖8所示。

圖 7 新型滑模觀測器系統(tǒng)的轉速響應圖Fig.7 Speed response diagram of a new sliding mode observer system

從圖7、8可以看出,系統(tǒng)的抗干擾能力良好,負載突然變化不會對系統(tǒng)造成很大的影響,都可以在0.02 s恢復到穩(wěn)態(tài)。

5 結 語

針對滑模觀測器抖振以及觀測輸出存在噪聲的問題,設計了改進二階濾波的滑模觀測器。滑模觀測器的切換抖振可以通過平滑切換函數(shù)以及引入自適應的切換增益來解決。觀測器輸出的噪聲可通過變截止頻率的低通濾波器進行更好的濾波,然后再加上卡爾曼濾波器進一步去除紋波分量,再進行角速度補償就可以得到更為準確的觀測結果。仿真結果表明改進的控制算法估算精度更高,魯棒性更好。