基于博弈論與模糊區間理論的森林康養基地評價方法

陳洪敏，黃慧萍，陳楚楚，李永超，崔文靜，張子超

基于博弈論與模糊區間理論的森林康養基地評價方法

陳洪敏1，黃慧萍1，陳楚楚1，李永超1，崔文靜1，張子超2

（三明學院 1.信息工程學院，2.三明學院-中興通訊ICT學院，福建 三明 361005）

為了提高森林康養基地等級劃分的精度，對相同等級下不同地區之間的優劣做出比較，提出了一種基于博弈論與模糊區間理論的森林康養基地評價方法，建立了區間型森林康養基地評價指標體系．利用博弈論將模糊熵與變異系數權重進行組合，借助模糊區間理論構建評價模型，并采用格貼近度公式得到待評價地區隸屬的等級，引入TOPSIS模型對所選取的待評價地區進行優劣排序．結果表明，該評價方法具有良好的適用性與有效性．

森林康養基地；博弈論組合賦權法；模糊區間綜合評價；格貼近度；等級評價

2016年，國家林業局印發《林業發展“十三五”規劃》明確提出要大力發展森林康養[1]．森林因其特殊功效，能夠滿足人們對于健康的需求，森林康養基地也隨之產生[2]．因此，對于森林康養基地的評價顯得至關重要．陳梅[3]等通過可視化分析，將森林康養基地指標體系歸納為政策型和學術型兩類．宋子健[4]使用理論分析法和專家咨詢法創建了主客觀交互下的多目標二次評價指標篩選體系，最終確立五個多目標共同評價指標，分別為生態環境質量、康養環境質量、康養主體需要程度、社會經濟效益與市場認知程度，得到森林康養基地適宜性綜合評價等級．費文君[5]等根據得分不同將森林康養基地類型劃分為綜合發展型、康復療養型、產業經營型和生態保育型，針對場地選址適宜性、接待能力指標與發展潛能指標三個方面構建指標體系，綜合運用層次分析法與主成分分析法計算評價指標權重，建立森林康養基地資源評價指標框架．晏琪[6]等通過頻數分析法確立初步森林康養空間評價指標體系，接著利用因子分析法，篩選構建出3個一級指標、6個二級指標和22個三級指標．宋子健[7]等使用交互式過濾產生法和理論分析法等最終構建46個指標，構造判斷矩陣得到指標權重，將森林康養區橫向劃為特優、優、良、中、差五個等級，縱向劃分為體驗型、產出型、附加型和失衡型四個類別．李瀟欣[8]采用主成分分析法和因子分析法找到關鍵影響因素，針對適宜性進行打分．任曉旭[9]等將森林康養旅游基地的生態資源指標體系分為森林自然特征、森林小氣候、空氣中保健物質和景觀美學四個類別，并利用KSSD經驗公式界定人體舒適度指數評價標準．楊春蘭[10]應用正靶心距的灰靶決策模型檢驗評價模型得出的結果，并在此基礎上劃分了森林康養基地建設等級．

現有模型大多采取了主觀賦權的方式確定指標的權重，使得評分結果精準度不高，同時也無法給出相同等級下各地區之間的優劣排序．考慮到森林康養的評價指標具有一定的模糊性和波動性，本文提出借助模糊區間理論建立綜合評價模型，通過博弈論將熵權法與變異系數權重進行組合，利用格貼近度確立待評價地區隸屬的等級并引入TOPSIS模型對其進行排序．通過多個地區康養等級評價，驗證了評價方法具有良好的適用性與有效性．該方法豐富完善了博弈論組合賦權、模糊區間綜合評價方法及其應用領域，同時,創新森林康養基地評價的相關理論，可以為森林康養基地的可持續發展提供理論依據和實踐參考．

1 森林康養基地等級評價模型

根據對森林康養基地資源的分析，并總結相關國家規范和行業標準，建立了以森林資源質量、空氣中的物質、環境和位置為一級指標，以近成熟林比例、森林覆蓋率、平均森林郁閉度、NH3體積濃度、PM10體積濃度、NO體積濃度、Tovc有機物污染體積濃度、CO2體積濃度、PM2.5體積濃度、負氧離子體積濃度、水環境、聲環境、土壤環境、太陽能年輻射總量、年平均溫度、風速、緯度、海拔和氣壓為二級指標的評價指標體系[11]（見表1）．

注：水環境采用地表水環境質量級別；土壤環境采用內梅羅綜合污染指數．

為便于說明，本文涉及的主要符號含義見表2.

表2 符號說明

等級性評價指標體系中近成熟林比例、森林覆蓋率、平均森林郁閉度、負氧離子體積濃度、水環境、太陽能年輻射總量、年平均溫度、風速、緯度、海拔、氣壓為效益型指標；NH3體積濃度PM10體積濃度、NO體積濃度、Tovc有機物污染體積濃度、PM2.5體積濃度、聲環境、土壤環境為成本型指標；CO2體積濃度為中間型指標.

在等級性評價中，各級指標數據的變化含義并不相同，因此將其轉化為無量綱的正向化區間模糊數．效益型指標、成本型指標、中間型指標的轉化公式分別為

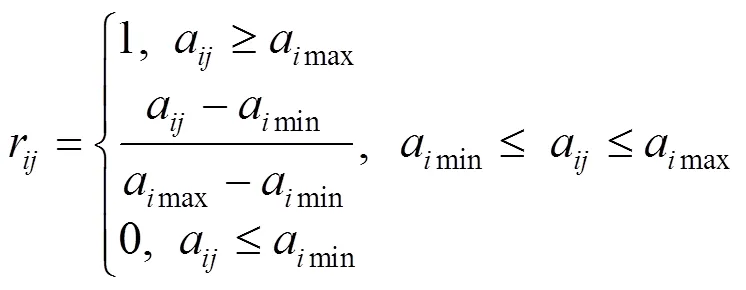
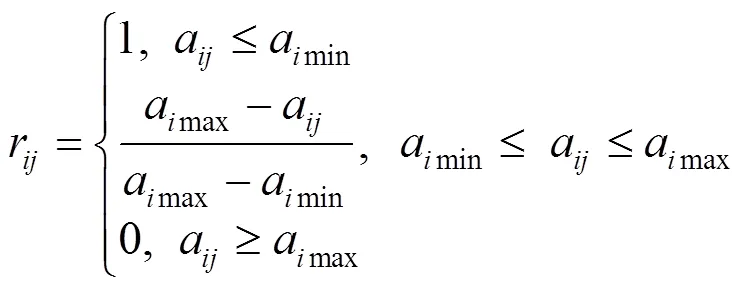
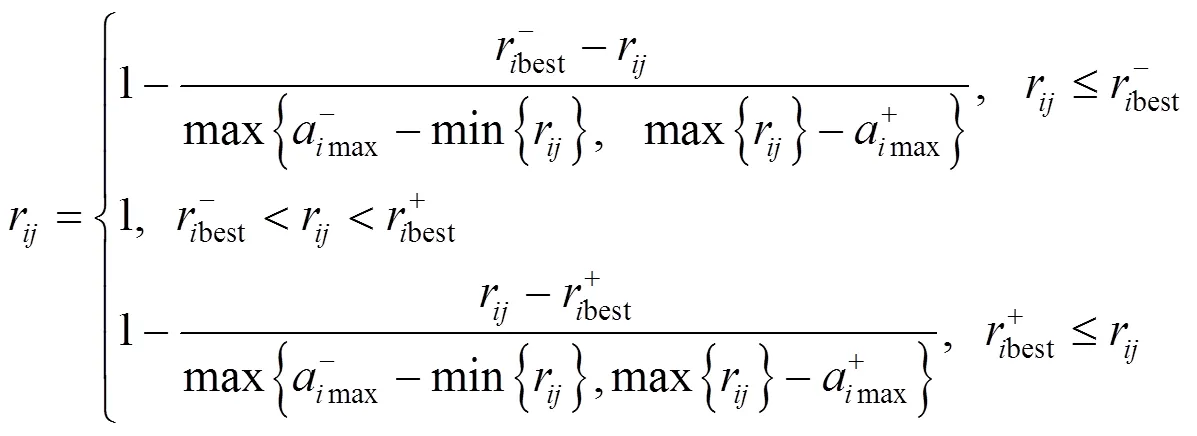
將表1中各指標數據按照式（1）～（3）進行計算，得到各級指標的相對取值（見表3）．

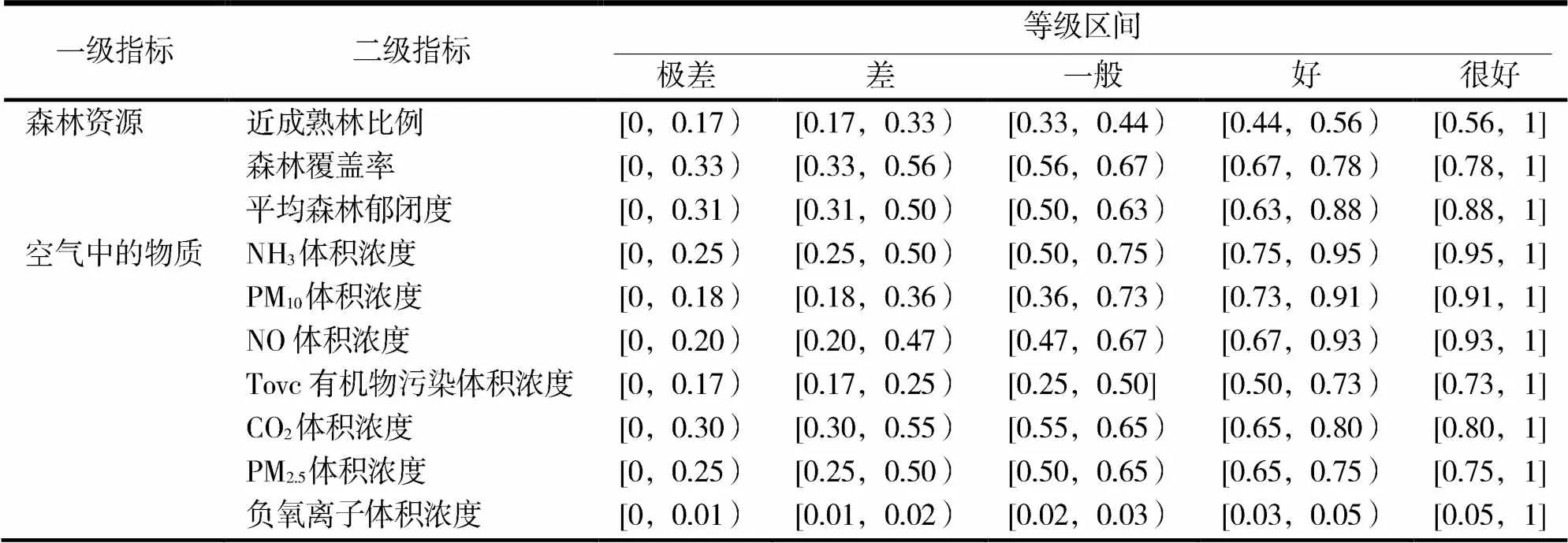
表3 森林康養基地等級評價指標模糊歸一正向化數據

續表3

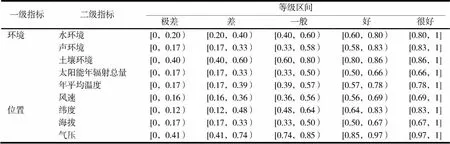
一級指標二級指標等級區間 極差差一般好很好 環境水環境[0，0.20）[0.20，0.40）[0.40，0.60）[0.60，0.80）[0.80，1] 聲環境[0，0.17）[0.17，0.33）[0.33，0.58）[0.58，0.83）[0.83，1] 土壤環境[0，0.40）[0.40，0.60）[0.60，0.80）[0.80，0.86）[0.86，1] 太陽能年輻射總量[0，0.17）[0.17，0.33）[0.33，0.50）[0.50，0.66）[0.66，1] 年平均溫度[0，0.17）[0.17，0.39）[0.39，0.57）[0.57，0.78）[0.78，1] 風速[0，0.16）[0.16，0.36）[0.36，0.56）[0.56，0.69）[0.69，1] 位置緯度[0，0.12）[0.12，0.48）[0.48，0.64）[0.64，0.83）[0.83，1] 海拔[0，0.17）[0.17，0.33）[0.33，0.50）[0.50，0.67）[0.67，1] 氣壓[0，0.41）[0.41，0.74）[0.74，0.85）[0.85，0.97）[0.97，1]

2 博弈論組合賦權法

2.1 變異系數確定權重

變異系數法[12]直接利用各項指標所包含的信息確定權重，本文通過對變異系數進行改進，得到了一種客觀賦權的方法．根據該方法，變化差異較大的指標權重較大，變化差異較小的指標權重較小，從而根據指標的統計學規律確定其重要程度.

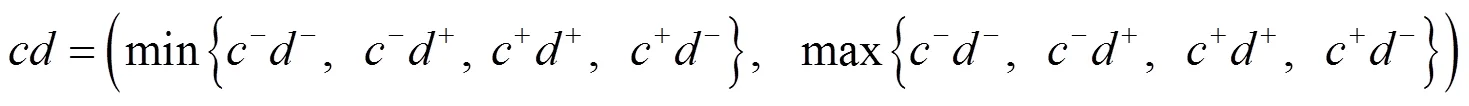
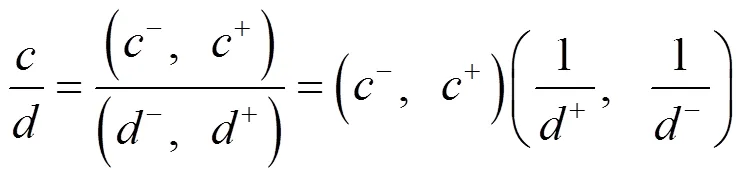
通過區間型數據的運算規則，即可得到區間型均值、方差和變異系數，具體計算方法為

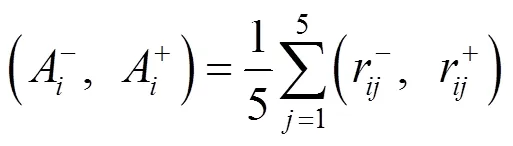
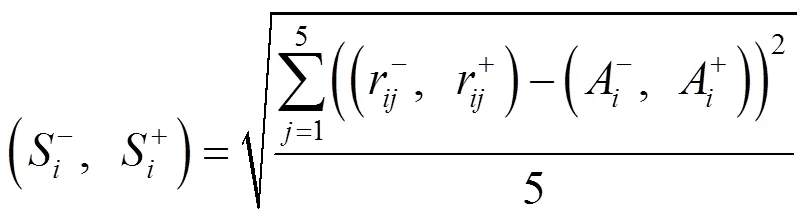
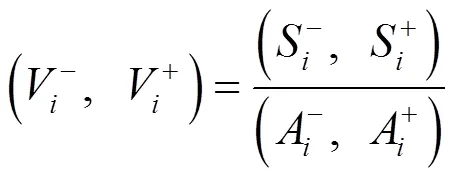
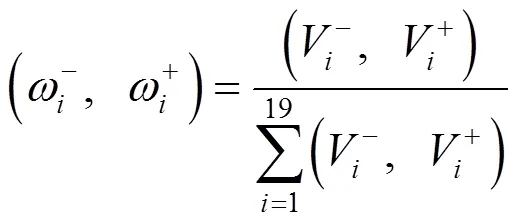
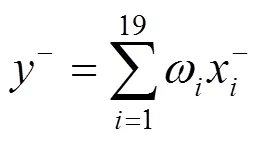
為使二級指標的綜合評價得分的下界小，上界大，確定森林康養等級評價的二級指標的多目標規劃優化函數[13]為

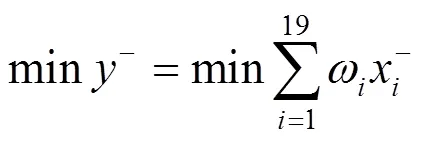
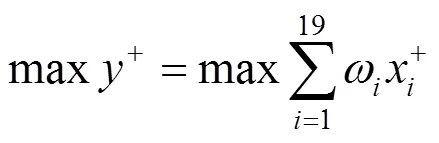
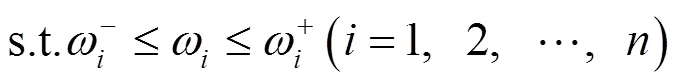
為了便于求解，將多目標函數轉換為單目標規劃

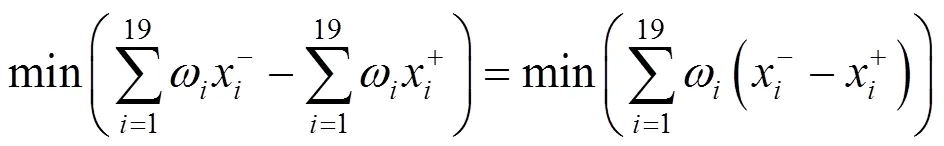
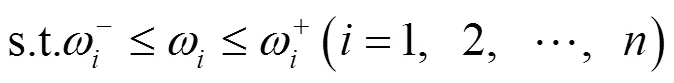
最終，通過該單目標規劃函數，各二級指標就可以在對應的區間型權重中尋得最優實數型權重．

2.2 構建模糊熵確定權重

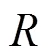
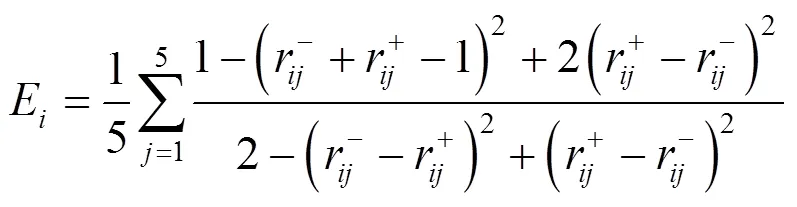
2.3 博弈論組合權重

博弈論是用于分析和研究參與主體的行為之間相互影響以及影響后決策均衡問題的理論．根據博弈論中的NASH均衡，為通過變異系數法和模糊熵確定的兩種權重尋求一致性．博弈論組合賦權法在多種權重間尋求最優線性組合，使得各權重間的偏差最小．其基本步驟為：

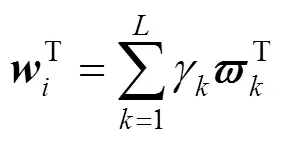
求最優加權線性組合使得離差最小化，即

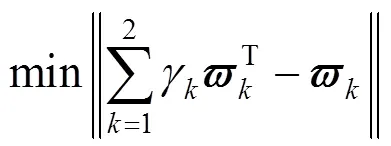
3 區間型模糊綜合評價及基于格貼進度的TOPSIS法

3.1 區間型二級模糊綜合評價

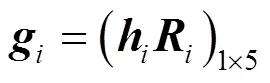
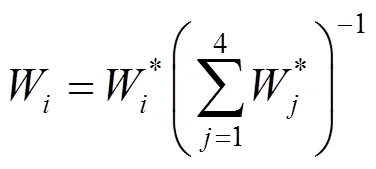
則得總評判斷矩陣為

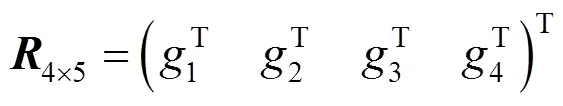
從而得到總綜合評價為

3.2 基于區間模糊數格貼進度的TOPSIS

TOPSIS法也可以稱為逼近理想解排序法，為了對待評價地區進行優劣排序，利用該方法計算每個地區的得分，進而可以得到最終排名．

區間模糊數的格貼近度公式為

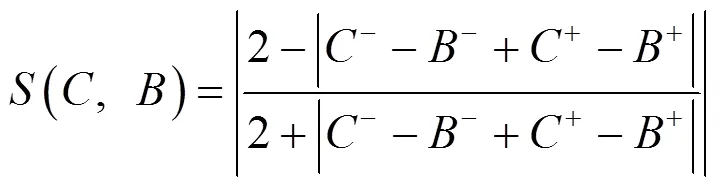
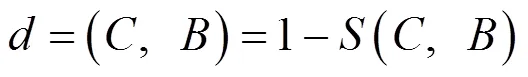
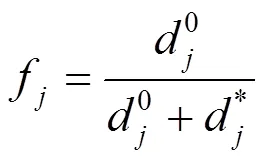
4 融合博弈論與模糊區間理論的森林康養基地評價步驟

融合博弈論與模糊區間理論的森林康養基地評價步驟為：

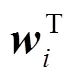
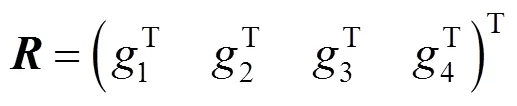
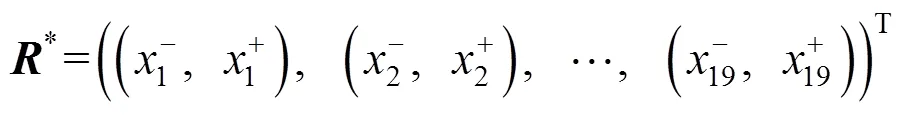
5 實例分析

以上海、北京、三明和麗水市為例進行實例分析，相關數據來源于各級政府部門的公報、中國環境監測總站、地理監測云平臺等官方相關網站[15-17]．以浙江省麗水市為例，其近成熟林比例為32%、森林覆蓋率為83%、平均森林郁閉度53%、NH3體積濃度為0.1 mg/m3、PM10體積濃度為29～40 μg/m3、NO體積濃度為0.001 mg/m3、Tovc有機物污染體積濃度為0.029～0.031 mg/m3、CO2體積濃度為230～300 mg/L、PM2.5體積濃度為17～19 μg/m3、負氧離子體積濃度為2 700 個/m3、水環境為0.8～1 mg/m3、聲環境為52.3～56.2 db、土壤環境（內梅羅綜合污染指數）為0.5、太陽能年輻射總量4 680～5 000 MJ/m2、年平均溫為18～20℃、風速為0.8～2.2 m/s、緯度為27.25～28.57°、海拔74～80 m、氣壓為101 100～101 200 Pa．

利用式（4）～（7），（12）～（16）得到各二級指標權重向量分別為

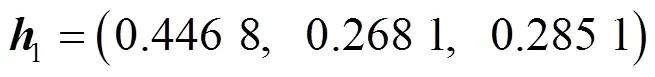
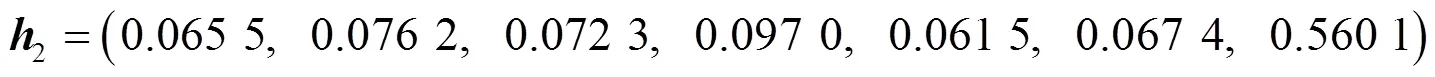
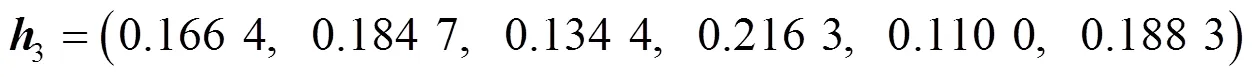
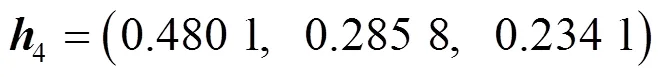
按照公式（17）（18）求得評價指標體系的二級因素集的綜合評價為

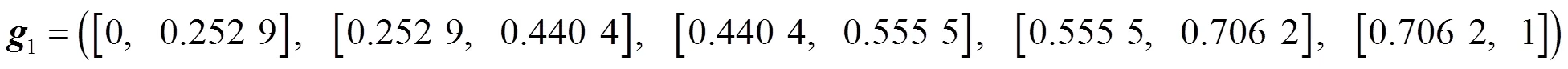
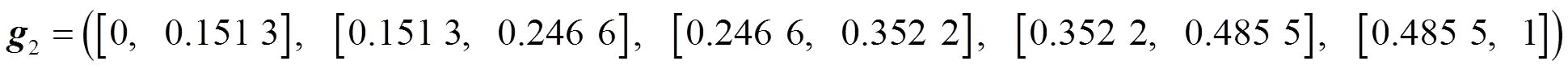
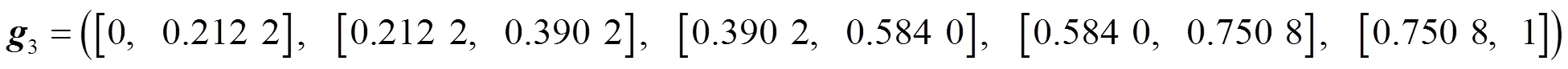
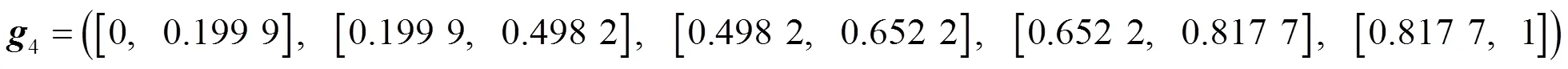
由式（20）（21）求得總綜合評價為

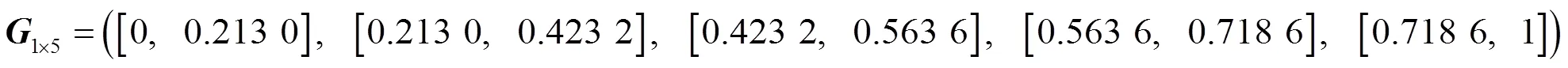
對麗水市的數據按照式（1）～（3）進行無量綱模糊化處理，得到麗水市評價矩陣

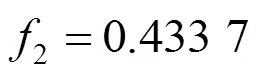
6 結語

考慮到森林康養指標體系的數據多具有區間性和模糊性，因此借助區間型模糊理論對森林康養評價模型進行數學建模．通過博弈論組合賦權法得到最優的權重線性組合，建立了區間模糊綜合評價模型，結合貼近度與TOPSIS模型，確立待評價地區的隸屬等級與優劣順序．通過對麗水、上海、北京、三明市這四個地區的數據進行分析，得到的結果為麗水和三明市隸屬的等級為好，上海和北京市隸屬的等級為一般．由于采用模糊區間數，使得等級評價結果更具有合理性，并解決了各待評價地區的排序問題，提高了排序精度．在未來的工作中，可以建立更完善的評價指標體系，使得森林康養的評價更加全面．同時，上述研究可以進一步推廣到水質等級與土壤環境評價等領域．

[1] 李露霏．“十三五”時期林業旅游與休閑產業發展分析[J]．農業與技術，2023，43（3）：160-162．

[2] 鄭貴軍，段菁陽，劉俊昌．森林康養產業發展的動力機理研究[J]．中南林業科技大學學報（社會科學版），2019，13 （2）：95-101．

[3] 陳梅，陶穎．森林康養基地指標體系評價研究[J]．中國林業經濟，2021（6）：103-106．

[4] 宋子健．森林康養基地適宜性評價研究[D]．上海：華東理工大學，2021．

[5] 費文君，劉思語，高祥飛．森林康養基地資源評價方法研究[J]．南京林業大學學報（自然科學版），2023（2）：1-11．

[6] 晏琪，劉苑秋，文野，等．基于因子分析的森林康養空間評價指標體系研究[J]．中國園林，2020，36（1）：81-86．

[7] 宋子健，溫全平．森林康養資源評價指標體系構建及評價：以蔡家川森林康養區為例[J]．林業科技情報，2020，52（1）：38-43．

[8] 李瀟欣．北京市國有林場發展森林康養的適宜性評價研究[D]．北京：北京林業大學，2020．

[9] 任曉旭，何禎．森林康養旅游基地生態資源評價體系構建研究[J]．文教資料，2021（4）：46-48，68．

[10] 楊春蘭．森林康養基地建設評價研究[D]．成都：西華大學，2020．

[11] 潘洋劉，曾進，文野，等．森林康養基地建設適宜性評價指標體系研究[J]．林業資源管理，2017（5）：101-107．

[12] 黃敏，周德紅，樊旭巖，等．基于兩種組合賦權法的天然氣長輸管道安全風險評估比較[J]．工業安全與環保，2023，49（2）：42-47．

[13] 郜燕群．基于最優區間權重的金融風險評價[J]．貴陽學院學報（自然科學版），2019，14（1）：34-38．

[14] 陳孝國，徐慧，徐源，等．基于直覺模糊集的煤礦應急救援能力評價研究[J]．大連大學學報，2015，36（6）：33-36．

[15] 麗水市人民政府．2021年麗水市生態環境狀況公報[EB/OL]．（2022-06-20）[2022-11-13]．http://www.lishui.gov.cn/art/2022/6/20/art_1229216407_57335516.html．

[16] 上海市人民政府．上海森林覆蓋率增至19.42%?去年固碳釋氧創造價值超38億元，綠色“家底”日益豐厚[EB/OL].（2022-10-27）[2022-11-13]．https://www.shanghai.gov.cn/nw4411/20221027/8c8fd3376bfc4e92b744c952a1ae0c4d.html.

[17] 中華人民共和國生態環境部．全國城市實時空氣質量、水質實時監測發布[EB/OL].（2021-12-30）[2022-11-13]．http://www.cnemc.cn.

Evaluation method of forest health base based on game theory and fuzzy interval theory

CHEN Hongmin1，HUANG Huiping1，CHEN Chuchu1，LI Yongchao1，CUI Wenjing1，ZHANG Zichao2

（1. School of Information Engineering，2. Sanming University-ZTE ICT College，Sanming University，Sanming 361005，China）

To improve the accuracy of the ranking of forest health base and compare the advantages and disadvantages of different areas under the same rank，an evaluation method of forest health base based on game theory and fuzzy interval theory is proposed，an interval-type forest health base evaluation index system is established．Game theory is used to combine fuzzy entropy and variation coefficient weight，then the evaluation model is constructed with the help of fuzzy interval theory，and the rank of the areas to be evaluated is obtained by using the lattice closeness formula，finally，the TOPSIS model is introduced to rank the selected areas for evaluation．The results show that the evaluation method has good applicability and validity.

forest health base；combination weighting approach of game theory；fuzzy interval comprehensive evaluation；lattice closeness；grade evaluation

O225∶S788.1

A

10.3969/j.issn.1007-9831.2024.01.006

1007-9831（2024）01-0022-08

2023-04-13

教育部協同育人項目（202102391036）；福建省中青年教師教育科研項目（JAT210423）；三明學院科學研究發展基金資助項目（B202104）；三明學院項目驅動創新班項目（CXB202017）；三明學院創業訓練計劃項目（X2023161X）

陳洪敏（1984-），男，福建莆田人，講師，碩士，從事數據挖掘和智能優化研究．E-mail：chm@fjsmu.edu.cn