基于多策略混合改進(jìn)HHO算法的WSN節(jié)點(diǎn)覆蓋優(yōu)化

張士榮，趙俊杰，談發(fā)明

(1.江蘇理工學(xué)院 信息中心，江蘇 常州 213001；2.江蘇理工學(xué)院 電氣信息工程學(xué)院，江蘇 常州 213001)

0 引 言

傳感器節(jié)點(diǎn)的部署及網(wǎng)絡(luò)覆蓋是決定WSN感知、通信質(zhì)量的關(guān)鍵，直接影響無線網(wǎng)絡(luò)的生存時(shí)間和網(wǎng)絡(luò)管理效率[1-3]。節(jié)點(diǎn)部署不佳會(huì)導(dǎo)致覆蓋盲區(qū)、節(jié)點(diǎn)密度過高和重復(fù)覆蓋、冗余節(jié)點(diǎn)多等問題，優(yōu)化WSN節(jié)點(diǎn)部署，以更少的WSN節(jié)點(diǎn)部署數(shù)量提高監(jiān)測(cè)區(qū)域覆蓋率將具有重要意義。

將WSN節(jié)點(diǎn)部署位置搜索與群體智能優(yōu)化算法相結(jié)合，可以利用智能算法優(yōu)異的隨機(jī)式和啟發(fā)式搜索機(jī)制加快節(jié)點(diǎn)部署位置的尋優(yōu)過程。哈里斯鷹算法HHO[4]是一種新的智能優(yōu)化算法，算法以哈里斯鷹種群對(duì)獵物的包圍、攻擊過程建立算法數(shù)學(xué)模型。該算法綜合性能較優(yōu)已廣泛應(yīng)用在圖像分割[5]、神經(jīng)網(wǎng)絡(luò)訓(xùn)練[6]、電力系統(tǒng)控制[7]、時(shí)差定位[8]等領(lǐng)域。但HHO算法本身還存在著易早熟收斂、求解精度低的不足。

為了解決WSN節(jié)點(diǎn)覆蓋優(yōu)化問題，本文設(shè)計(jì)一種改進(jìn)哈里斯鷹優(yōu)化算法MHIHHO求解節(jié)點(diǎn)覆蓋優(yōu)化問題。為了提高HHO算法的性能，設(shè)計(jì)Fuch無限折疊混沌初始化策略對(duì)種群進(jìn)行初始化；利用自適應(yīng)精英個(gè)體對(duì)立學(xué)習(xí)提高候選解質(zhì)量；引入正余弦優(yōu)化改進(jìn)局部開發(fā)中軟/硬包圍的跳躍式位置更新，提高局部尋優(yōu)能力；結(jié)合柯西與拉普拉斯最優(yōu)解變異實(shí)現(xiàn)變異，使算法跳離局部極點(diǎn)。結(jié)果表明，改進(jìn)哈里斯鷹算法MHIHHO在優(yōu)化WSN節(jié)點(diǎn)覆蓋率方面實(shí)現(xiàn)了預(yù)期效果。

1 相關(guān)研究現(xiàn)狀

智能優(yōu)化算法因具有較強(qiáng)的全局搜索能力，近年來被廣泛應(yīng)用于WSN節(jié)點(diǎn)覆蓋優(yōu)化問題。文獻(xiàn)[9]提出混合遺傳與差分進(jìn)化的多目標(biāo)覆蓋優(yōu)化算法，實(shí)現(xiàn)了傳感節(jié)點(diǎn)的優(yōu)化部署。文獻(xiàn)[10]利用虛擬力對(duì)傳統(tǒng)PSO進(jìn)行優(yōu)化，將節(jié)點(diǎn)覆蓋率提升了5%。文獻(xiàn)[11]提出外推改進(jìn)人工蜂群算法，應(yīng)用于WSN節(jié)點(diǎn)部署優(yōu)化后，模型的覆蓋率有所提高，但結(jié)果依然存在10%左右盲區(qū)。文獻(xiàn)[12]提出改進(jìn)灰狼優(yōu)化算法，節(jié)點(diǎn)覆蓋率提升了4%，但節(jié)點(diǎn)分布均勻性仍有不足。文獻(xiàn)[13]則引入了種群分布熵和平均粒距的概念，雖然覆蓋率接近于90%，但依然沒有解決好盲區(qū)。文獻(xiàn)[14]提出改進(jìn)鯨魚優(yōu)化算法，網(wǎng)絡(luò)覆蓋監(jiān)測(cè)效率有所提高。文獻(xiàn)[15]利用改進(jìn)果蠅算法對(duì)傳感節(jié)點(diǎn)覆蓋率和連通性進(jìn)行優(yōu)化，部署效果優(yōu)于蟻群算法。有關(guān)哈里斯鷹算法的改進(jìn)也有一些相關(guān)研究，但還未檢索到應(yīng)用在節(jié)點(diǎn)部署優(yōu)化問題中的文獻(xiàn)，在HHO算法改進(jìn)工作上，文獻(xiàn)[16]結(jié)合偽反射學(xué)習(xí)機(jī)制設(shè)計(jì)新型哈里斯鷹算法QRHHO，一定程度提升了算法尋優(yōu)精度。文獻(xiàn)[17]結(jié)合混沌遍歷、規(guī)律、隨機(jī)思想改進(jìn)HHO，以混沌映射增強(qiáng)初始種群多樣性，并結(jié)合模擬退火對(duì)算法局部最優(yōu)跳離能力進(jìn)行改進(jìn)。文獻(xiàn)[18]結(jié)合長(zhǎng)期記憶法提高算法全局搜索能力。文獻(xiàn)[19]引入方形鄰域拓?fù)涓倪M(jìn)種群個(gè)體組成，通過縱橫雙向隨機(jī)覓食提高HHO開發(fā)能力。文獻(xiàn)[20]引入偽反向?qū)W習(xí)提高HHO初始種群的多樣性，進(jìn)一步提升算法收斂速度。

以上基于智能優(yōu)化算法的WSN節(jié)點(diǎn)覆蓋優(yōu)化策略，雖然可以有效優(yōu)化節(jié)點(diǎn)部署，但智能算法本身存在尋優(yōu)精度差和易于得到局部最優(yōu)的缺陷，且在搜索與精細(xì)開采過程的平衡、避免局部最優(yōu)等綜合性能上仍有一些不足。因此，針對(duì)WSN節(jié)點(diǎn)覆蓋率的提升和均勻度方面的優(yōu)化工作仍然有進(jìn)一步的研究空間。

2 HHO算法及其多策略混合改進(jìn)算法

2.1 HHO算法

HHO過程由搜索與開發(fā)兩個(gè)階段組成。兩個(gè)階段的切換則由獵物的逃逸能量系數(shù)E決定，不同E值會(huì)引導(dǎo)哈里斯鷹展現(xiàn)不同的捕食模式。能量系數(shù)E定義為

E=2E0(1-t/Tmax)

(1)

式中：t為當(dāng)前迭代，Tmax為算法最大迭代次數(shù)，E0為獵物的初始能量，且E0=2r1-1，r1為[0，1]間的隨機(jī)量。式(1)表明：獵物的逃逸能量在算法迭代過程中將在(-1，1)間變化。

(1)全局搜索階段

若滿足 |E|≥1， HHO進(jìn)入全局搜索階段。此時(shí)，哈里斯鷹將依據(jù)隨機(jī)選擇個(gè)體和目標(biāo)個(gè)體的位置對(duì)自身的位置進(jìn)行更新，數(shù)學(xué)模型如

Xi(t+1)=

(2)

(3)

式中：Xrand(t)、Xi(t)、Xrabbit(t) 分別指迭代t時(shí)隨機(jī)選擇個(gè)體位置、個(gè)體i原位置、種群全局最優(yōu)個(gè)體位置，Xi(t+1) 為個(gè)體i的更新位置，q、ri(i=1，2，3，4) 為(0，1)間的隨機(jī)量，[lb，ub] 為個(gè)體搜索邊界值，Xm(t) 為個(gè)體位置均值，N為哈里斯鷹的種群規(guī)模。

(2)局部開發(fā)階段

若滿足 |E|<1， HHO進(jìn)入局部開發(fā)階段。此時(shí)，哈里斯鷹擁有4種不同的策略完成對(duì)獵物的捕食：軟包圍、硬包圍、漸進(jìn)式快速俯沖軟包圍和漸進(jìn)式快速俯沖硬包圍。而選擇哪種策略由獵物逃逸能量系數(shù)E和逃逸概率λ決定。

1)若滿足 |E|≥0.5且λ≥0.5，表明存在逃逸能量，此時(shí)的數(shù)學(xué)模型如

(4)

式中：ΔX(t) 為獵物與個(gè)體間距，r5為隨機(jī)量，J為逃逸跳躍值。

2)若 |E<0.5且λ≥0.5， 表明不存在逃逸能量，個(gè)體將以硬包圍方式對(duì)獵物發(fā)起突襲，數(shù)學(xué)模型如

Xi(t+1)=Xrabbit(t)-E|ΔX(t)|

(5)

3)若滿足 |E|≥0.5且λ<0.5， 表明獵物仍有充足能量逃逸，哈里斯鷹將以漸進(jìn)式快速俯沖軟包圍方式圍捕獵物，并實(shí)時(shí)糾正圍捕位置和方向，數(shù)學(xué)模型如

Xi(t+1)=

(6)

式中：D為搜索位置維度，S為大小為D×1的(0，1)間隨機(jī)行向量，LF() 為服從Levy飛行分布的函數(shù)，計(jì)算方法為

(7)

式中：μ、v為(0，1)間隨機(jī)量，β=1.5。

4)若滿足 |E|<0.5且λ<0.5， 表明獵物能量快耗盡，哈里斯鷹將以漸進(jìn)式快速俯沖硬包圍方式圍捕獵物，該數(shù)學(xué)模型如

Xi(t+1)=

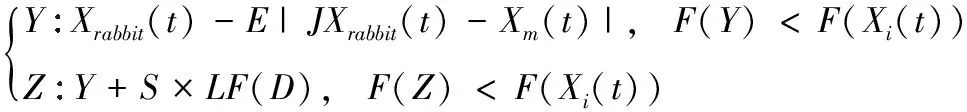
(8)

2.2 多策略混合改進(jìn)哈里斯鷹算法MHIHHO

2.2.1 Fuch無限折疊混沌初始化策略

初始種群的分布對(duì)于算法的尋優(yōu)效率具有很大影響。由于HHO算法對(duì)于最優(yōu)解的所在區(qū)域并無先驗(yàn)知識(shí)可用，故采用了隨機(jī)初始化方法，會(huì)導(dǎo)致個(gè)體分布均勻性差，個(gè)體質(zhì)量下降，影響算法尋優(yōu)速度。混沌系統(tǒng)具有遍歷性、非重復(fù)兼顧了隨機(jī)性的特點(diǎn)，有著比完全隨機(jī)分布更均勻的特征。常用的混沌映射系統(tǒng)如Logistic映射、Tent映射和Circle映射等，但這些都屬于有限折疊混沌映射。相比而言，F(xiàn)uch混沌映射是一種可無限折疊的混沌映射方式，其遍歷性、動(dòng)態(tài)隨機(jī)性以及最后的收斂性都要優(yōu)于前面3種混沌映射。故MHIHHO引入Fuch無限折疊混沌方式對(duì)HHO進(jìn)行種群初始化操作，以生成個(gè)體在搜索空間內(nèi)的初始位置信息。Fuch混沌映射公式為

y(k+1)=cos(1/y(t)2)

(9)

式中：y(k)≠0。 生成Fuch混沌值后，混沌值與種群搜索空間的映射規(guī)則為

X(t)=lb+y(t)×(ub-lb)

(10)

式中：[lb，ub] 為個(gè)體搜索邊界，y(t) 為式(9)生成的Fuch混沌值。

圖1是以隨機(jī)初始化和Fuch混沌初始化得到的種群分布。隨機(jī)初始化方式為

圖1 兩種種群初始化分布

X(t)=lb+rand×(ub-lb)

(11)

顯然，隨機(jī)初始化中個(gè)體重疊覆蓋問題較為嚴(yán)重，F(xiàn)uch混沌初始化的均勻性更好，能夠更均勻地對(duì)解空間遍歷。雖然算法對(duì)最優(yōu)解所在區(qū)域并無先驗(yàn)知識(shí)，但更均勻的個(gè)體分布將提升算法尋覓最優(yōu)解的搜索效率和穩(wěn)定性。

圖2是在基準(zhǔn)函數(shù)Booth的測(cè)試下，MHIHHO分別利用隨機(jī)初始化、Logistic映射初始化、Circle映射初始化以及Fuch無限折疊混沌初始化策略得到的目標(biāo)函數(shù)收線曲線。Sphere函數(shù)的理論最優(yōu)解為0。算法進(jìn)行500次迭代，搜索區(qū)域內(nèi)布置30個(gè)個(gè)體。觀察4個(gè)曲線，3種混沌映射初始化方法對(duì)函數(shù)的求解精度顯然優(yōu)于隨機(jī)化方法，隨機(jī)初始化在50個(gè)數(shù)據(jù)級(jí)的精度下一直處于平緩，最后收斂，在300次迭代后已經(jīng)無法進(jìn)一步提高收斂精度。3種混沌映射均有不同程度精度提高，但趨勢(shì)各異。隨機(jī)種群初始化在迭代約300次后尋優(yōu)精度已經(jīng)穩(wěn)定，無法進(jìn)一步開辟新空間，提升搜索精度。利用混沌種群初始化可以進(jìn)一步提高搜索精度。所提Fuch無限折疊映射初始迭代初期搜索精度不是最優(yōu)，但后期精度迅速提升，得益于該初始化方法能夠使個(gè)體更均勻的分布，遍歷到所有未及區(qū)域，以更高的概率逼近最優(yōu)目標(biāo)，提升多樣性。

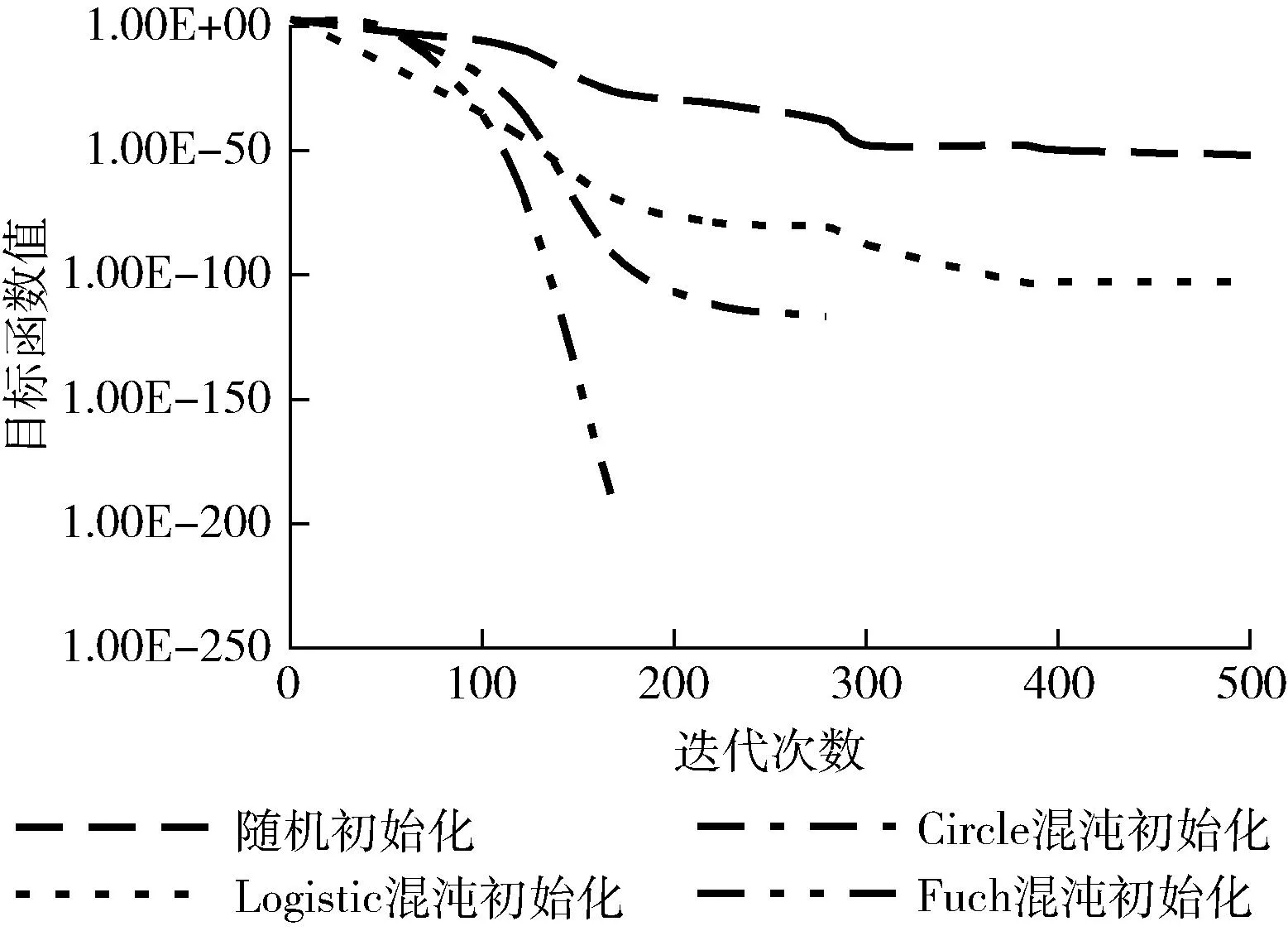
圖2 不同混沌初始化策略對(duì)比

2.2.2 自適應(yīng)精英個(gè)體對(duì)立學(xué)習(xí)策略

研究表明，種群個(gè)體經(jīng)對(duì)立變異后擁有更大的概率靠近最優(yōu)解區(qū)域，種群可行解的質(zhì)量可有效提高。為了擴(kuò)展搜索區(qū)域，提高HHO的全局搜索能力，MHIHHO引入自適應(yīng)精英個(gè)體對(duì)立學(xué)習(xí)策略對(duì)HHO進(jìn)行改進(jìn)。令X表示一個(gè)種群個(gè)體，即問題的一個(gè)可行解，搜索空間范圍為 [lb，ub]， 定義個(gè)體X的對(duì)立解X′為

X′=lb+(ub-X)

(12)

若種群所有個(gè)體進(jìn)行對(duì)立學(xué)習(xí)，勢(shì)必會(huì)增加算法時(shí)間復(fù)雜度，而若個(gè)體適應(yīng)度較差，其對(duì)立解對(duì)種群搜索方向引導(dǎo)也有不利。此外，HHO通過模擬哈里斯鷹的種群捕食過程，目標(biāo)(食物源)的信息決定了種群個(gè)體位置更新，決定著算法進(jìn)化方向。若目標(biāo)已經(jīng)處于局部最優(yōu)，則種群個(gè)體會(huì)向局部極值點(diǎn)靠攏，影響算法尋優(yōu)精度。利用精英個(gè)體組成的種群有利于避免單一個(gè)體在尋優(yōu)中發(fā)生早熟收斂。改進(jìn)算法將進(jìn)一步對(duì)精英個(gè)體進(jìn)行對(duì)立學(xué)習(xí)，以自適應(yīng)比例設(shè)置精英個(gè)體數(shù)量，進(jìn)行對(duì)立學(xué)習(xí)。將種群中精英個(gè)體的數(shù)量定義為

(13)

式中：nelite為種群所選精英個(gè)體數(shù)量，N為種群個(gè)體總數(shù)，t為算法當(dāng)前迭代次數(shù)，Tmax為算法總迭代次數(shù)。根據(jù)式(13)，精英個(gè)體的數(shù)量將隨著算法迭代線性遞減。迭代早期，精英個(gè)體數(shù)量較多，可以盡可能發(fā)揮個(gè)體對(duì)立解的優(yōu)勢(shì)，得到更多適應(yīng)度較優(yōu)的候選解；迭代后期，精英個(gè)體數(shù)量逐步減少，可以加快算法收斂，降低算法時(shí)間復(fù)雜度。具體過程為：先計(jì)算種群個(gè)體適應(yīng)度，按適應(yīng)度對(duì)個(gè)體進(jìn)行升序排列，選取前nelite個(gè)個(gè)體為精英個(gè)體，計(jì)算精英個(gè)體的對(duì)立解，并利用貪婪選擇策略保留適應(yīng)度較優(yōu)的個(gè)體至下一代種群中。

2.2.3 正余弦優(yōu)化策略

當(dāng)HHO迭代時(shí)，個(gè)體搜索維度其實(shí)在變小，即搜索空間逐步壓縮，種群多樣性逐步缺失。為了提升HHO的全局搜索能力，MHIHHO將引入正余弦優(yōu)化機(jī)制SCA[21]對(duì)HHO的局部開發(fā)過程進(jìn)行優(yōu)化。具體針對(duì)MHIHHO中軟/硬包圍時(shí)的跳躍位置更新。

已知正余弦優(yōu)化中粒子個(gè)體的位置更新方式為

xi，j(t+1)=

(14)

式中：xbest，j為全局最優(yōu)解的j維位置，r6為振幅調(diào)節(jié)因子，r7∈[0，2π]、r8∈[-2，2]、r9∈[0，1]均為均勻分布隨機(jī)量。

結(jié)合式(14)，將軟/硬包圍階段的跳躍式位置更新方式定義為

X(t+1)=

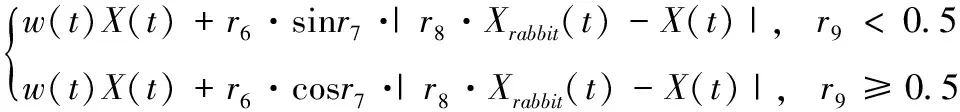
(15)

式中：r6為振幅調(diào)節(jié)因子，用于均衡全局搜索與局部開發(fā)。若r6值較大，算法可以更大的步長(zhǎng)提升全局搜索能力，而較小的r6值則可以使算法在局部范圍內(nèi)作精細(xì)開發(fā)。為了提高改進(jìn)算法的尋優(yōu)能力，本文結(jié)合指數(shù)函數(shù)將r6的更新改進(jìn)為非線性遞減，定義為

r6(t)=(1+βt)·rmax·e-βt

(16)

式中：β表示曲線調(diào)整參數(shù)，rmax表示振幅調(diào)節(jié)系數(shù)的最大值。由此可見，r6將隨迭代非線性從最大值遞減到最小值，更好地在搜索與開發(fā)間進(jìn)行轉(zhuǎn)換。

慣性權(quán)重w(t) 的思想源于粒子群算法，MHIHHO進(jìn)一步引入該因子在迭代前期以更大權(quán)重值增強(qiáng)個(gè)體位置對(duì)種群的影響，迭代后期以更小權(quán)重值增強(qiáng)最優(yōu)個(gè)體引導(dǎo)，具體為

(17)

式中：k為調(diào)整系數(shù)，wmax、wmin分別是權(quán)重最大值和最小值。

2.2.4 高斯與拉普拉斯最優(yōu)個(gè)體變異策略

HHO算法的位置更新公式表明，隨著迭代進(jìn)化，種群搜索將向著最優(yōu)解移動(dòng)，逐步聚集于最優(yōu)解鄰域，這可能導(dǎo)致因多樣性缺失帶來的局部最優(yōu)解。為此，MHIHHO引入一種針對(duì)種群最優(yōu)解的混合變異策略，使得搜索個(gè)體具有跳離局部最優(yōu)、擴(kuò)展搜索空間的能力。混合變異策略由高斯變異和拉普拉斯變異機(jī)制構(gòu)成。

已知高斯分布的概率密度函數(shù)為

(18)

拉普拉斯分布的概率密度函數(shù)為

(19)

式中：m為高斯分布均值，n為變量；a∈(-∞，+∞)， 表示位置，b為比例參數(shù)，且b>0。

利用式(20)的分布函數(shù)定義拉普拉斯分布L(a，b)， 該函數(shù)關(guān)于位置參數(shù)a對(duì)稱分布

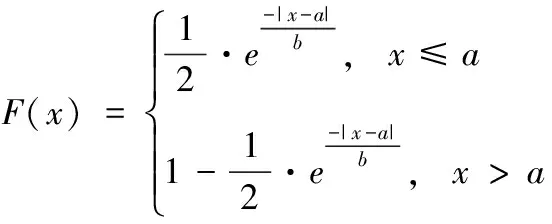
(20)

為了充分利用搜索空間的隨機(jī)性，增強(qiáng)種群多樣性，設(shè)拉普拉斯分布L(a，b) 中a=1，b=2。高斯分布G(m，n) 中m=0，n=1。將針對(duì)種群最優(yōu)解Xrabbit的混合變異方式定義為

Xrabbit(t+1)=(η1·L(1，2)+η2·G(0，1)+1)·Xrabbit(t)

(21)

(22)

拉普拉斯分布L(1，2) 擁有比高斯分布G(0，1) 更大的波動(dòng)。而兩個(gè)系數(shù)η1和η2均是迭代t的指數(shù)函數(shù)，根據(jù)式(22)，系數(shù)η1迭代早期更大，有利于拓展搜索空間；迭代后期，η1漸漸減小，收斂加快。同時(shí)，系數(shù)η2不斷增加，高斯系數(shù)G(0，1) 此時(shí)利于精細(xì)開采，提高局部開發(fā)能力。

3 基于MHIHHO的WSN節(jié)點(diǎn)覆蓋優(yōu)化模型

3.1 覆蓋模型

將WSN節(jié)點(diǎn)部署于矩形區(qū)域，節(jié)點(diǎn)部署后不具備移動(dòng)性，且節(jié)點(diǎn)均為同質(zhì)結(jié)構(gòu)。WSN節(jié)點(diǎn)具備感知能力，能夠發(fā)現(xiàn)其通信半徑內(nèi)其它WSN節(jié)點(diǎn)。現(xiàn)令部署區(qū)域大小為S=L×M，可將其視為L(zhǎng)×M的網(wǎng)格，單個(gè)網(wǎng)格大小為1。WSN節(jié)點(diǎn)部署數(shù)量為V，表示為集合Z={Z1，Z2，…，ZV}， 所有節(jié)點(diǎn)為同質(zhì)結(jié)構(gòu)，具有相同的感知半徑r和通信半徑R，通常r≤2R。令 {xi，yi} 為節(jié)點(diǎn)Zi的坐標(biāo)位置，i=1，2，…，V。

令點(diǎn)oj坐標(biāo)為 {xj，yj}， 以歐氏距離度量方式計(jì)算傳感節(jié)點(diǎn)Zi與oj的距離為

(23)

若d(Zi，oj)≤r， 則oj被Zi覆蓋。定義oj被Zi感知的概率為

(24)

為了提升監(jiān)測(cè)區(qū)域內(nèi)的感知概率，多個(gè)WSN節(jié)點(diǎn)可以協(xié)同進(jìn)行感知。則點(diǎn)oj的聯(lián)合感知概率為

(25)

則監(jiān)測(cè)區(qū)域的覆蓋率即為所有WSN節(jié)點(diǎn)覆蓋的目標(biāo)點(diǎn)數(shù)量與區(qū)域內(nèi)總目標(biāo)點(diǎn)數(shù)量的比值，定義為

(26)

3.2 利用MHIHHO算法求解WSN節(jié)點(diǎn)覆蓋問題

算法優(yōu)化目標(biāo)是：利用若干數(shù)量WSN節(jié)點(diǎn)部署于監(jiān)測(cè)區(qū)域S，求解節(jié)點(diǎn)部署最優(yōu)位置，使目標(biāo)區(qū)域的覆蓋率Pcov達(dá)到最大化。此時(shí)，覆蓋優(yōu)化問題可視為目標(biāo)函數(shù)的搜索問題，算法的最優(yōu)解為各WSN節(jié)點(diǎn)的部署位置，而哈里斯鷹個(gè)體的位置則為WSN節(jié)點(diǎn)的覆蓋分布。對(duì)于一個(gè)搜索哈里斯鷹個(gè)體，其2d-1維位置為節(jié)點(diǎn)d的橫坐標(biāo)，2d維位置則為節(jié)點(diǎn)d的縱坐標(biāo)。具體步驟如下：

輸入：區(qū)域大小L×M、傳感節(jié)點(diǎn)數(shù)V、感知半徑r；種群規(guī)模n、迭代總數(shù)Tmax、搜索范圍 [lb，ub]、rmax、 系數(shù)k、權(quán)重值wmax和wmin；

輸出：WSN節(jié)點(diǎn)部署位置及最優(yōu)覆蓋率Pcov；

步驟1 輸入MHIHHO算法參數(shù)和WSN參數(shù)；

步驟2 在搜索空間內(nèi)利用Fuch無限折疊混沌策略初始化哈里斯鷹種群；

步驟3 令當(dāng)前迭代t=1；

步驟4 執(zhí)行自適應(yīng)精英個(gè)體對(duì)立學(xué)習(xí)策略；并計(jì)算個(gè)體適應(yīng)度，確定當(dāng)前最優(yōu)解；

步驟5 根據(jù)式(1)更新獵物逃逸能量系數(shù)E；

步驟6 若 |E|≥1且q≥0.5， 根據(jù)式(2)中的第1個(gè)公式更新個(gè)體位置；若 |E|≥1且q<0.5，利用式(2)中的第2個(gè)公式更新個(gè)體位置；

步驟7 若 |E|≥0.5且λ≥0.5， 根據(jù)式(15)的正余弦優(yōu)化策略更新個(gè)體位置；

步驟8 若 |E|≥0.5且λ<0.5， 利用式(6)更新個(gè)體位置；

步驟9 若 |E|<0.5且λ≥0.5， 先利用式(5)更新個(gè)體位置；

步驟10 若 |E|<0.5且λ<0.5， 根據(jù)式(15)的正余弦優(yōu)化策略更新個(gè)體位置；

步驟11 返回種群更新后的位置，并更新最優(yōu)解；利用式(21)柯西和拉普拉斯分布對(duì)最優(yōu)解進(jìn)行變異，并擇優(yōu)保留；

步驟12 更新迭代t=t+1；

步驟13 判斷終止條件，若未終止則返回步驟4；否則，輸出最優(yōu)解，即：對(duì)應(yīng)的WSN節(jié)點(diǎn)部署的位置坐標(biāo)及最優(yōu)覆蓋率Pcov。

圖3是MHIHHO求解覆蓋優(yōu)化問題的流程。

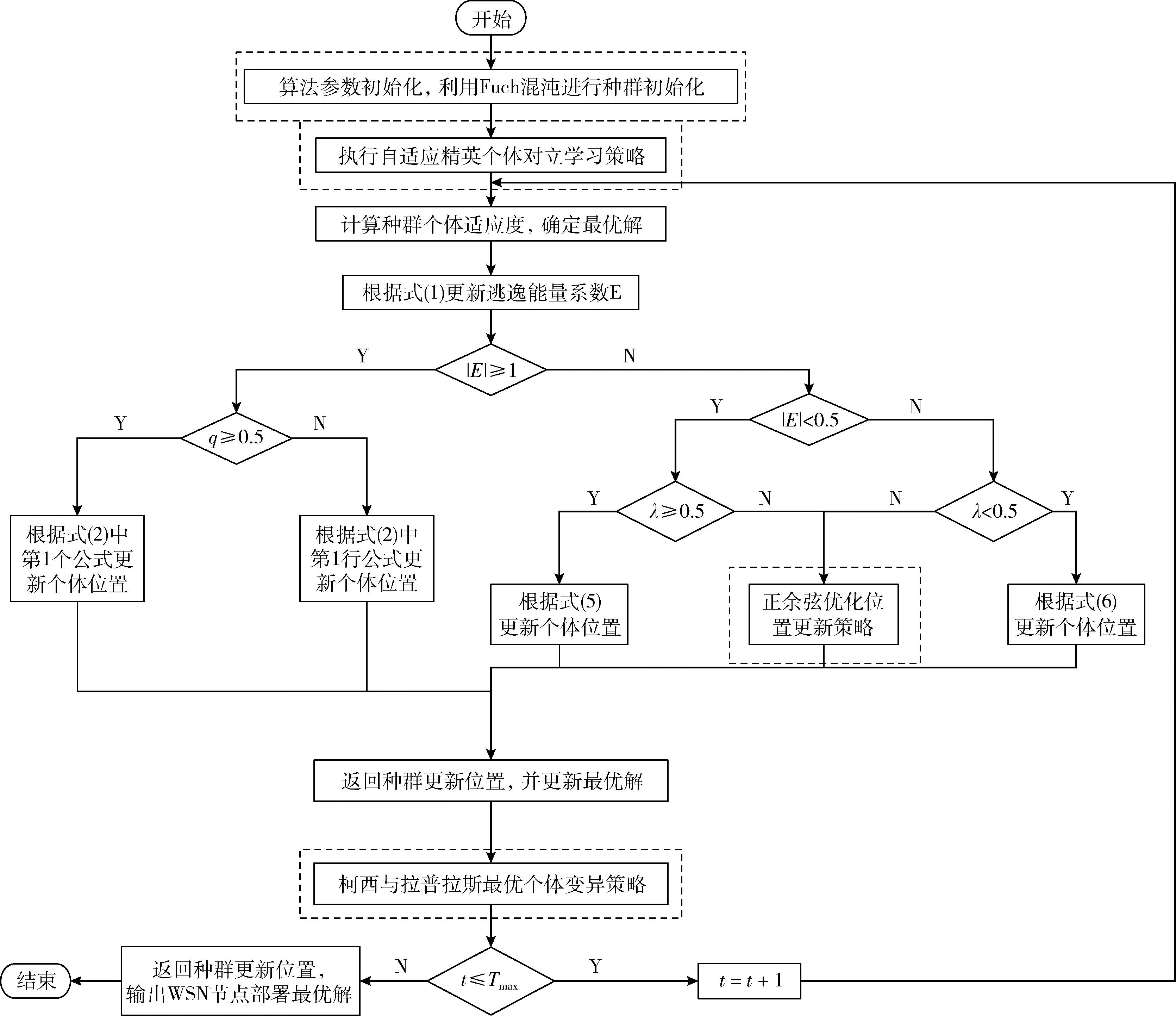
圖3 MHIHHO算法求解流程

4 仿真實(shí)驗(yàn)

4.1 基準(zhǔn)函數(shù)尋優(yōu)實(shí)驗(yàn)

為了驗(yàn)證MHIHHO的有效性，先利用6個(gè)基準(zhǔn)函數(shù)式進(jìn)行目標(biāo)函數(shù)的尋優(yōu)實(shí)驗(yàn)，表1是基準(zhǔn)函數(shù)相關(guān)屬性。表中，基準(zhǔn)函數(shù)f(x) 即為尋找最優(yōu)解的目標(biāo)函數(shù)，搜索范圍為種群個(gè)體的活動(dòng)空間，fmin為函數(shù)理論可達(dá)的最優(yōu)值。同時(shí)，在表1中，函數(shù)f1(x)～f3(x) 為單峰函數(shù)類型，f4(x)～f6(x) 為多峰函數(shù)類型。為了兼顧公平性，算法獨(dú)立運(yùn)行20次，并計(jì)算其適應(yīng)度均值、標(biāo)準(zhǔn)方差、最優(yōu)值。算法的種群規(guī)模n=30，搜索維度d=20，迭代總次數(shù)Tmax=500，振幅調(diào)節(jié)系數(shù)最大值rmax=2，調(diào)整系數(shù)k=2，權(quán)重最大值wmax=0.9，wmin=0.3。仿真平臺(tái)為Matlab2019a。選擇標(biāo)準(zhǔn)哈里斯鷹優(yōu)化算法HHO[4]、改進(jìn)灰狼優(yōu)化算法IGWO[12]和改進(jìn)哈里斯鷹優(yōu)化算法QRHHO[16]與本文的MHIHHO同時(shí)作縱橫向?qū)Ρ确治觥?/p>

表1 基準(zhǔn)函數(shù)說明

(1)尋優(yōu)精度對(duì)比。表2是各算法在基準(zhǔn)函數(shù)上的尋優(yōu)結(jié)果。可以看出，MHIHHO在6個(gè)基準(zhǔn)函數(shù)中的4個(gè)可以取得理論最優(yōu)值，尋優(yōu)成功率達(dá)到66.7%，未取得理論最優(yōu)值的Schwefel2.21和Schwefel2.26中依然得到了最高的求解精度。而得到了更小的標(biāo)準(zhǔn)方差值，則表明MHIHHO具有更好的穩(wěn)定性和魯棒性。相比HHO，MHIHHO在求解精度上平均可以提高約4個(gè)數(shù)量級(jí)，與另外兩種改進(jìn)的群體智能算法QRHHO和IGWO相比也有較大程度的求解精度提高，說明MHIHHO所引入針對(duì)HHO的不同進(jìn)化階段所做的改進(jìn)工作對(duì)標(biāo)準(zhǔn)HHO中的搜索與開發(fā)的均衡、提升收斂速度和尋優(yōu)精度的改進(jìn)是切實(shí)有效可行的。

表2 算法尋優(yōu)結(jié)果

(2)收斂性對(duì)比。圖4進(jìn)一步選取兩個(gè)單峰基準(zhǔn)函數(shù)f2(x)、f3(x) 和兩個(gè)多峰基準(zhǔn)函數(shù)f5(x)、f6(x) 共4個(gè)基準(zhǔn)函數(shù)測(cè)試算法的尋優(yōu)收斂曲線。觀察曲線趨勢(shì)，MHIHHO在4個(gè)基準(zhǔn)函數(shù)上都表現(xiàn)出更快的收斂速度，在f2(x)、f3(x)、f5(x)、f6(x) 上都得到了很好的性能表現(xiàn)，

圖4 收斂曲線

其產(chǎn)生收斂的迭代次數(shù)也是最少的。尤其在兩個(gè)多峰函數(shù)上，由于具有多個(gè)極值點(diǎn)，波峰不定，算法的搜索過程容易到達(dá)局部最優(yōu)而無法進(jìn)化。MHIHHO通過引入基于混合柯西與拉普拉斯變異的動(dòng)態(tài)擾動(dòng)機(jī)制能夠使算法具備跳離局部最優(yōu)的能力，提高多峰函數(shù)中的尋優(yōu)性能。

(3)種群分布對(duì)比。選取基準(zhǔn)函數(shù)Schwefel2.21進(jìn)行實(shí)驗(yàn)，觀察算法在迭代100次、200次和400次時(shí)種群個(gè)體在搜索空間內(nèi)的分布，種群規(guī)模設(shè)為30。如圖5是不同時(shí)期算法種群個(gè)體的分布圖。HHO和IGWO在3個(gè)不同的迭代時(shí)期中，個(gè)體在搜索空間內(nèi)一直處于比較分散的狀態(tài)。迭代后期，甚至一些個(gè)體離最優(yōu)解區(qū)域依然相隔較遠(yuǎn)，已經(jīng)陷入局部最優(yōu)而無法脫離，這表明算法本身搜索性能還有待提升。相比而言，改進(jìn)算法QRHHO全局收斂性能更好，迭代后期一些個(gè)體已經(jīng)聚集在最優(yōu)解區(qū)域，表明算法中采用的偽反射學(xué)習(xí)機(jī)制使HHO種群實(shí)現(xiàn)了一定的信息交互，提升了算法搜索精度。MHIHHO總體上在迭代前、中、后期具備更好的分布，前期比較分散，保證種群多樣性，中期逐步聚集于最優(yōu)解附近，后期多數(shù)個(gè)體已經(jīng)逐步收斂于最優(yōu)解或鄰近區(qū)域。MHIHHO通過混合多策略改進(jìn)思路對(duì)HHO的改進(jìn)是行之有效的。

圖5 種群個(gè)體分布

4.2 WSN節(jié)點(diǎn)覆蓋優(yōu)化實(shí)驗(yàn)

令監(jiān)測(cè)區(qū)域大小S=100 m×100 m， 部署的WSN傳感節(jié)點(diǎn)總數(shù)V=30，節(jié)點(diǎn)感知半徑r=12 m，通信半徑R=24 m。仿真平臺(tái)為Matlab2019a。選擇標(biāo)準(zhǔn)哈里斯鷹優(yōu)化算法HHO[4]、改進(jìn)灰狼優(yōu)化算法IGWO[12]、改進(jìn)哈里斯鷹優(yōu)化算法QRHHO[16]與本文的MHIHHO算法進(jìn)行性能比較。

(1)WSN節(jié)點(diǎn)分布對(duì)比。圖6為分別利用HHO算法、IGWO算法、QRHHO算法和MHIHHO算法求解WSN節(jié)點(diǎn)部署位置后得到的區(qū)域覆蓋優(yōu)化情況，圖中黑實(shí)心點(diǎn)代表一個(gè)傳感器節(jié)點(diǎn)的部署坐標(biāo)，而圓形弧線區(qū)域則代表相應(yīng)傳感器節(jié)點(diǎn)所覆蓋的范圍，數(shù)字為傳感器節(jié)點(diǎn)的編號(hào)。可以看到，HHO算法得到的節(jié)點(diǎn)部署結(jié)果中，節(jié)點(diǎn)分布均勻性較差，存在多個(gè)覆蓋盲區(qū)，而部分區(qū)域又存在節(jié)點(diǎn)密度過高、覆蓋重復(fù)和冗余較大的問題，說明其尋優(yōu)性能還有待改進(jìn)。IGWO算法經(jīng)過節(jié)點(diǎn)位置和使用節(jié)點(diǎn)數(shù)量的優(yōu)化后，區(qū)域覆蓋更加均勻，明顯減少了高密度節(jié)點(diǎn)覆蓋區(qū)域，區(qū)域覆蓋率有所提高，但依然存在一些覆蓋空洞。利用本文的MHIHHO算法進(jìn)行節(jié)點(diǎn)覆蓋優(yōu)化后，節(jié)點(diǎn)分布更加均勻，節(jié)點(diǎn)使用數(shù)量又進(jìn)一步降低，幾乎不產(chǎn)生任何冗余節(jié)點(diǎn)和高密度重復(fù)覆蓋區(qū)域，覆蓋率接近于100%。

圖6 傳感節(jié)點(diǎn)部署

(2)WSN節(jié)點(diǎn)組網(wǎng)拓?fù)鋵?duì)比。基于圖6所得的WSN節(jié)點(diǎn)分布，利用普里姆算法構(gòu)建最小生成樹，結(jié)果如圖7所示。在節(jié)點(diǎn)通信距離均勻性上，MHIHHO優(yōu)于對(duì)比算法。同時(shí)，在MHIHHO所構(gòu)建的WSN通信網(wǎng)絡(luò)中，承接數(shù)據(jù)聚合的匯聚節(jié)點(diǎn)能夠更好地分布在區(qū)域邊緣，避免了中心位置，這樣避免了長(zhǎng)距離數(shù)據(jù)傳輸，降低了遠(yuǎn)距離數(shù)據(jù)傳送的能耗。綜合來看，智能優(yōu)化算法能夠一定程度上以提高網(wǎng)絡(luò)覆蓋率為目標(biāo)優(yōu)化節(jié)點(diǎn)的位置，但MHIHHO的平均通信距離分布更加均勻，匯聚節(jié)點(diǎn)分布更佳。

圖7 WSN節(jié)點(diǎn)組網(wǎng)

(3)覆蓋率對(duì)比。圖8是算法迭代過程中，覆蓋率的變化收斂曲線。可以看到，首先，從迭代完成后的最終區(qū)域覆蓋率上講，MHIHHO算法的覆蓋率接近于100%，是4種算法中最高。QRHHO算法、IGWO算法和HHO算法的覆蓋率分別達(dá)到93.6%、91.8%和83.2%，之所以無法進(jìn)一步提高覆蓋率，在于此時(shí)算法在求解最佳節(jié)點(diǎn)部署位置時(shí)已經(jīng)得到局部最優(yōu)解，該結(jié)果也驗(yàn)證MHIHHO算法在求解精度上得到有效提升。同時(shí)，從得到相同覆蓋率所使用的迭代次數(shù)上看，MHIHHO明顯使用了更少的迭代次數(shù)，說明算法的進(jìn)化速度更快，在相同條件下，能夠以相同數(shù)量節(jié)點(diǎn)得到更高的區(qū)域覆蓋率，節(jié)點(diǎn)部署位置更精確。圖9展示W(wǎng)SN節(jié)點(diǎn)部署數(shù)量對(duì)覆蓋率的影響。隨著部署節(jié)點(diǎn)數(shù)量的增加，區(qū)域覆蓋率都有所增加，但從覆蓋率增漲速度上看，MHIHHO算法明顯更快，并且在相同部署數(shù)量下，該算法的覆蓋率也是最高的。此外，當(dāng)部署節(jié)點(diǎn)較少時(shí)，在相對(duì)廣闊的監(jiān)測(cè)區(qū)域內(nèi)，較少節(jié)點(diǎn)幾乎不存在交叉覆蓋區(qū)域，所有4種算法的覆蓋率比較接近。但增加節(jié)點(diǎn)數(shù)量后，MHIHHO算法的覆蓋率明顯增加的更快，在160個(gè)節(jié)點(diǎn)數(shù)時(shí)，已經(jīng)接近于完全覆蓋，說明算法不僅求解精度更高，而且收斂速度更快，可更少部署節(jié)點(diǎn)數(shù)得到更高的區(qū)域覆蓋率。

圖8 覆蓋率隨迭代變化

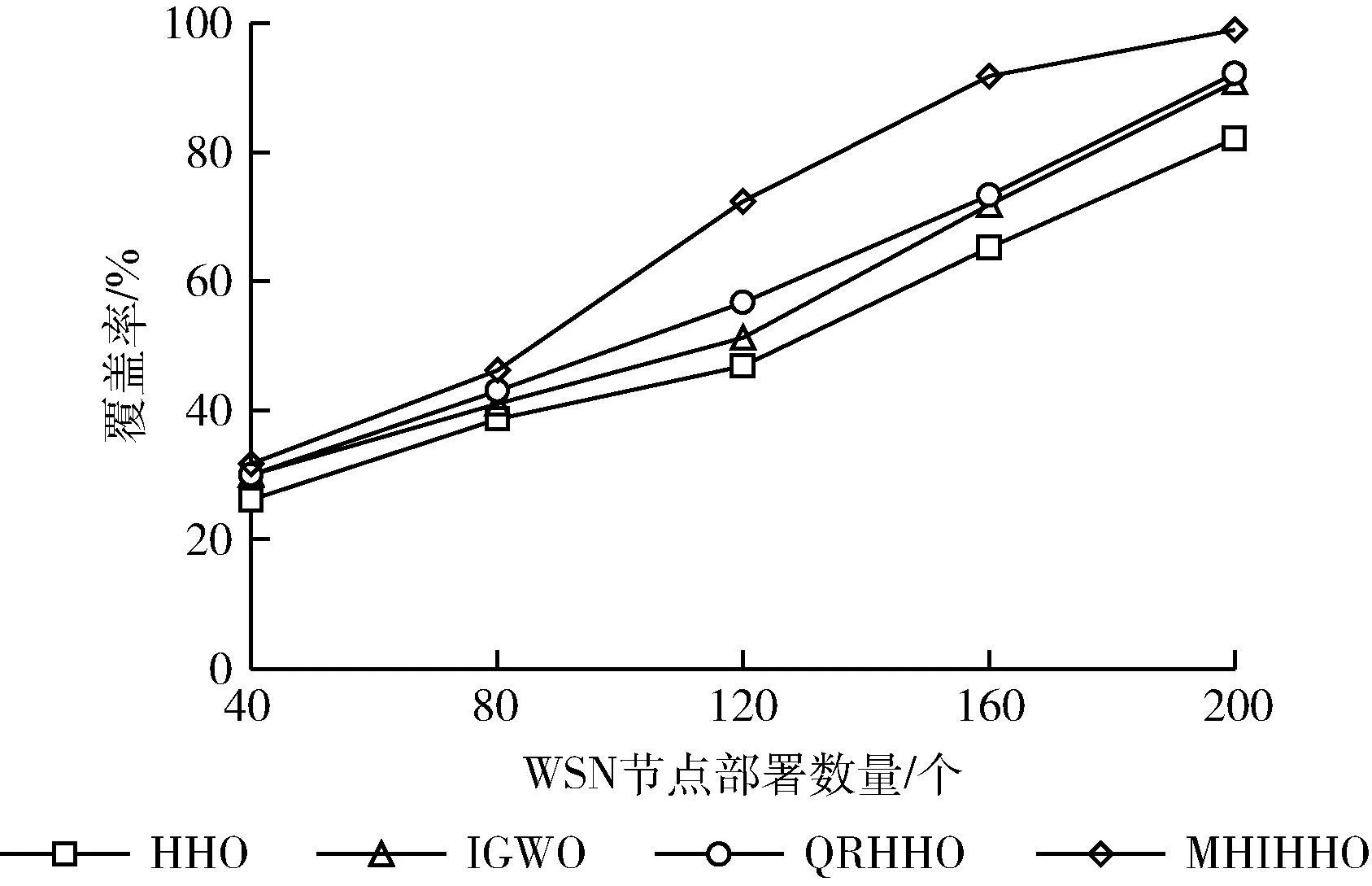
圖9 部署節(jié)點(diǎn)數(shù)量對(duì)覆蓋率的影響

(4)WSN生存時(shí)間對(duì)比。圖10是利用Leach作為組網(wǎng)協(xié)議，網(wǎng)絡(luò)工作后節(jié)點(diǎn)數(shù)量的變化情況。節(jié)點(diǎn)初始能量為0.5 J，采用常規(guī)能耗模型計(jì)算能耗[22]。由結(jié)果可知，MHIHHO算法的節(jié)點(diǎn)死亡慢于HHO算法、IGWO算法和QRHHO算法，若節(jié)點(diǎn)分布均勻性差，會(huì)導(dǎo)致冗余節(jié)點(diǎn)多，從而加快能耗。而未覆蓋區(qū)域數(shù)據(jù)中繼傳輸過多同樣會(huì)加快節(jié)點(diǎn)能耗。MHIHHO的數(shù)據(jù)傳輸距離均勻，遠(yuǎn)距離傳輸和近距離的冗余傳輸更少，節(jié)點(diǎn)工作時(shí)間更長(zhǎng)，可以延長(zhǎng)網(wǎng)絡(luò)生存時(shí)間。

圖10 網(wǎng)絡(luò)生存時(shí)間

表3是覆蓋所有目標(biāo)點(diǎn)時(shí)不同算法所需要的節(jié)點(diǎn)數(shù)的比較情況。仍然以30個(gè)傳感節(jié)點(diǎn)進(jìn)行部署，在完成相同覆蓋率的情況下，對(duì)比各算法所使用的節(jié)點(diǎn)數(shù)量情況。從結(jié)果中可以看到，在完成相同區(qū)域覆蓋率的情況下，MHIHHO算法能夠以更少數(shù)量的傳感器節(jié)點(diǎn)進(jìn)行部署，說明算法所利用的對(duì)節(jié)點(diǎn)位置的搜索機(jī)制能夠得到最佳的坐標(biāo)，盡可能地減少了交叉覆蓋的情況。對(duì)比算法由于存在對(duì)區(qū)域的冗余覆蓋，導(dǎo)致相同數(shù)據(jù)的節(jié)點(diǎn)部署下得到的覆蓋率相對(duì)較低。綜合說明改進(jìn)算法能夠求解到最優(yōu)的節(jié)點(diǎn)部署位置，以更少的部署節(jié)點(diǎn)得到更高的區(qū)域覆蓋率。

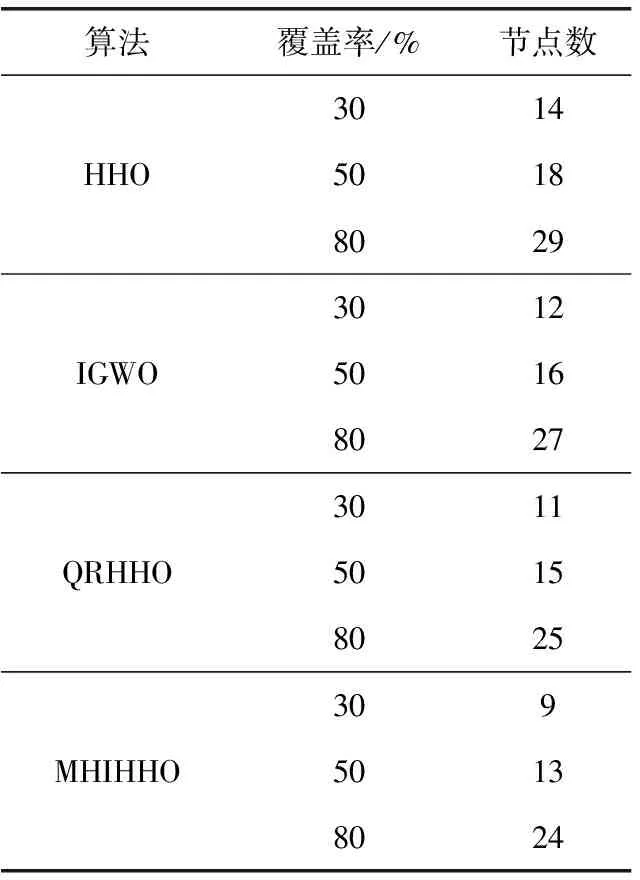
表3 節(jié)點(diǎn)使用數(shù)量對(duì)比

MHIHHO算法時(shí)間復(fù)雜度分析。令種群規(guī)模為n，搜索維度為d，算法迭代總次數(shù)為Tmax。種群初始化階段的時(shí)間復(fù)雜度為O(nd)， 執(zhí)行精英個(gè)體對(duì)立學(xué)習(xí)過程的最大時(shí)間復(fù)雜度為O(nd)。 接著算法需要以4種不同的方式更新個(gè)體位置，且該過程需要迭代Tmax次。該過程的時(shí)間復(fù)雜度為O(ndTmax)。 個(gè)體變異時(shí)間復(fù)雜度為O(ndTmax)。 則MHIHHO時(shí)間復(fù)雜度為O(nd+nd+ndTmax+ndTmax)=O(ndTmax)。

5 結(jié)束語

本文提出一種多策略混合改進(jìn)哈里斯鷹算法的WSN節(jié)點(diǎn)覆蓋優(yōu)化算法。首先，為了提高標(biāo)準(zhǔn)哈里斯鷹算法HHO的尋優(yōu)性能，引入Fuch無限折疊混沌初始化、自適應(yīng)精英個(gè)體對(duì)立學(xué)習(xí)、正余弦優(yōu)化、柯西/拉普拉斯變異對(duì)算法進(jìn)行改進(jìn)。應(yīng)用改進(jìn)算法求解WSN節(jié)點(diǎn)覆蓋優(yōu)化，以覆蓋率最大為目標(biāo)，求解節(jié)點(diǎn)最佳位置。結(jié)果表明，改進(jìn)算法實(shí)現(xiàn)了預(yù)期結(jié)果，能夠優(yōu)化網(wǎng)絡(luò)覆蓋率。未來研究方向可進(jìn)一步改善哈里斯鷹算法的全局搜索能力，在尋優(yōu)廣度和精度做一些改進(jìn)，從而達(dá)到覆蓋率的最大提升。