考慮場址危險一致性的中國完備條件目標譜與記錄選取

汪維依，冀 昆，溫瑞智，任葉飛

(1.中國地震局工程力學研究所中國地震局地震工程與工程振動重點實驗室，黑龍江，哈爾濱 150080；2.地震災害防治應急管理部重點實驗室，黑龍江，哈爾濱 150080；3.河海大學土木與交通學院，江蘇，南京 210024)

隨著結構彈塑性時程分析越發普遍，如何選取合適的地震動輸入進行結構抗震分析受到越來越多的關注。在相同的抗震設防烈度與場地條件下，《建筑抗震設計規范》[1]給出的目標譜是基本一致的。但不同地區、不同場址所處的具體地震地質構造環境與地震活動性水平都存在較大差異，僅僅依據抗震設計規范給出的峰值加速度和設計目標譜確定地震動輸入是不夠的。除了考慮目標結構特性之外，合理的地震動輸入應保證所選地震動與目標場址的概率地震危險性分析(Probabilistic seismic hazard analysis, PSHA)的結果相匹配。也就是說，地震動輸入是基于概率地震危險性水平而不是地震動強度指標(Intensity measures, IM)來確定。一旦工程結構和所在場址確定，結構響應指標的年超越概率曲線是不受地震動輸入選擇影響的。要實現這一點，就要保證地震動輸入盡可能“真實”地反映當地可能遭受地震的“危險性水平”。這樣可以極大降低地震動輸入不確定性造成的響應結果差異，這就是危險一致地震動輸入的核心思想[2]。確定危險一致地震動的一般思路是：概率地震危險性分析—危險一致目標譜—記錄匹配—確定地震動輸入。可以看到，危險一致地震動輸入的核心環節是目標譜的構建與記錄匹配。

一致概率譜(Uniform hazard spectrum, UHS)本質上就是最早基于危險一致思想構造的目標譜，在國內外得到了廣泛應用，比如我國重大工程的地震安全性評價中就以UHS 為地震動輸入的目標譜[3]。其構建思路是，確定目標地震危險性水平下不同周期點的IM(如加速度反應譜值Sa等)，得到整體譜型具有相同超越概率的目標譜。UHS 具有三個理論缺陷：① UHS 的各個周期點的Sa值都是單獨通過PSHA 確定的，彼此相互獨立，但實際上某條天然地震動的反應譜不可能在所有周期下都有一致的超越概率；② UHS 無法找到對應的唯一的設定地震，因為不同Sa的最大貢獻設定地震事件并不相同；③ UHS 僅考慮了均值，沒有給出記錄間離散性的定義[4]。用UHS 作為目標反應譜選擇地震動用于結構的非線性動力分析，結果偏大。針對缺陷1 和缺陷2，BAKER和ALLIN[5]提出了條件均值譜(Conditional mean spectrum, CMS)的概念。CMS 以目標周期T*(一般選擇結構的基本振動周期)下的譜加速度Sa(T*)作為目標值，借助Sa的地震動預測方程和Sa相關系數矩陣確定其余周期點Sa在Sa(T*)條件下的取值。如果通過條件高斯分布將條件離散性也考慮進去，得到的結果為條件譜(Conditional spectrum)[6-7]。計算時，若使用平均或者最大貢獻設定地震和單一地震動預測方程，這樣得到的條件譜稱之為粗略條件譜。若將PSHA 過程中涉及的多個設定地震事件與不同地震動預測方程的邏輯樹權重都考慮進去，則稱之為完備條件譜。針對粗略條件譜我國近年來也有了較多研究成果，如韓建平等[8]針對CMS 對不同結構響應的離散性控制以及譜型參數在易損性分析的作用進行了研究；呂大剛等[9-10]銜接西安市地震危險性分析結果進行了CMS 構建；以及冀昆等[11-12]提出針對重大工程地震安全性評價產出的狹義CMS/CS 構建流程。但是上述研究主要針對粗略條件譜，關于完備條件譜的研究尚未充分開展。在作者的前期研究中，采用我國五代區劃圖相同的潛源分布與地震動衰減關系，進行了中國主要城市的危險性分析與設定地震解耦[13]，為本文計算完備條件譜提供了基礎。

除了構建危險一致目標譜外，另一個需要考慮的問題就是，如何實現強震動記錄與目標譜的匹配。對于服從多元高斯分布的“粗略”條件譜，可以通過拉丁超立方抽樣方法等手段實現，由均值和協方差矩陣得到服從目標分布的模擬反應譜，進而逐一匹配模擬譜實現記錄的選取。借助貪心優化算法等思路[14]，可實現對CS 目標均值與標準差的高效匹配。但是，對于完備條件譜來說，其不再滿足多元高斯分布，由于無法定義高斯混合分布的協方差矩陣，只能采用兩步蒙特卡羅抽樣的思路生成模擬譜，進而采用假設檢驗直接對Sa指標的累積概率分布是否“接近”目標分布作為記錄選取依據[15]。這種記錄選取方法雖然保證了Sa指標分布與目標分布接近，但是實踐中發現無法保證工程更感興趣的均值與標準差的較好匹配，而且過程較為繁瑣[13]，需要生成數百條模擬譜才可以保證與完備條件譜的理論分布接近。由于我國的條件譜在構建過程中并不存在多個衰減關系邏輯加權，高斯混合分布的協方差矩陣理論上和多元高斯分布之間差異性有限。如果將高斯混合分布的協方差矩陣進行近似，那么就可以采用粗略條件譜的匹配思路進行記錄選取，本文將提出適用于我國完備條件譜的記錄匹配思路。

本文利用前期研究中給出的我國主要城市的地震概率危險性分析結果，分別給出了基于二維設定地震解耦結果的“粗略”條件譜，和基于三維設定地震結果的完備條件譜。之后以北京近郊某城市為例，進行了兩種條件譜的對比討論，探討了加速度反應譜相關系數對條件譜的影響，最后給出了適用于我國完備條件譜的高效記錄匹配方法。基于完備條件譜選取的地震動記錄與場址的地震危險性一致，可服務于新一代的基于性態的地震工程(performance-based earthquake engineering,PBEE)[16]中的結構需求指標概率危險性計算[17]。作為全概率PBEE 方法中連接概率地震危險性分析和結構易損性分析[18-19]的橋梁，基于完備條件譜選取地震動輸入有著承上啟下的作用。

1 完備條件譜構建方法

1.1 銜接我國五代區劃圖的設定地震解耦

筆者在前期工作[13]中，采用與我國五代地震參數區劃圖一致的地震動三級潛源劃分與衰減關系，在OpenQuake[20]平臺上進行了中國大陸的地震概率危險性分析，進一步給出了各個主要城市的設定地震解耦結果。對于中國大陸的34 個主要城市，研究得到的峰值地面加速度值基本位于第五代地震危險圖給出的區間范圍內，驗證了結果與我國現行地震動參數區劃圖[21]是基本一致的。同時給出了平均重現期為475 年和2475 年的Pga和Sa值在周期為0.2 s、0.3 s、0.5 s、0.7 s、1.0 s、1.5 s 和2.0 s 時的超越概率曲線和設定地震解耦結果(https://github.com/JIKUN1990/China-Seismic-Haz ard-Deaggregation-34cities)。后文將要用到的北京近郊某城市的二維(震級-距離)設定地震解耦和三維(震級-經緯度)解耦結果如圖1 所示。圖中方柱的不同高度代表重現期為2475 年周期為1.0 s 下各個設定地震事件微元的貢獻率，其中，圖1(a)中的方柱表示的是每個震級-距離微元的貢獻率，圖1(b)中不同邊框線型的方柱表示的是該城市研究區域內(120 km 內)的各個潛源中不同經緯度柵格點在各震級下的貢獻率。

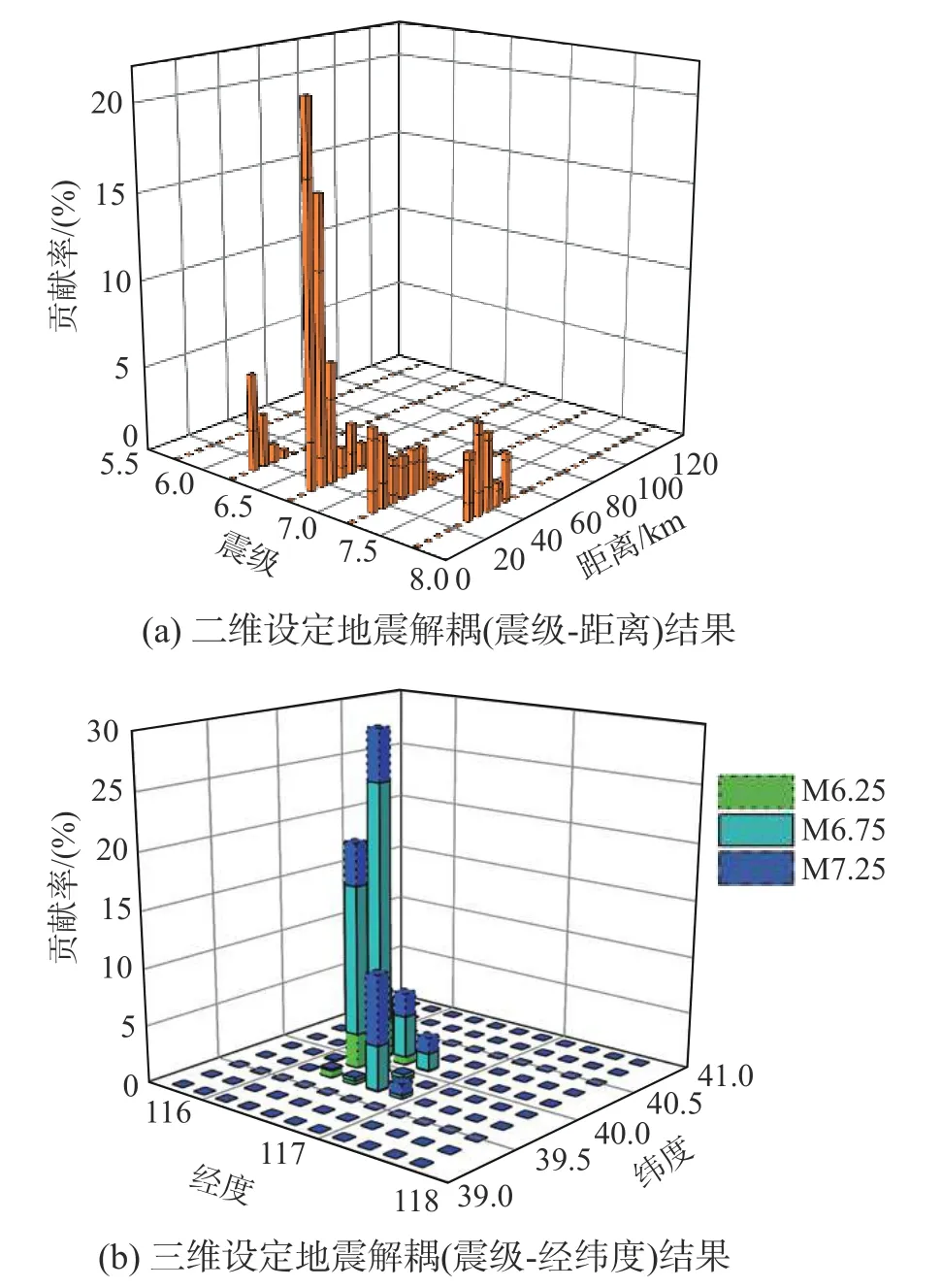
圖1 重現期2475 年下周期1.0 s 的設定地震解耦結果Fig.1 Disaggregation of earthquakes with a period of 1.0 s under the return period of 2475 years

1.2 粗略與完備條件目標譜構建

1) 銜接二維設定地震的粗略條件目標譜構建

首先，在給定危險性水平下，基于二維設定地震解耦結果得到不同震級-距離(M,R)地震事件的貢獻率。通過對貢獻率進行加權平均或者采用最大貢獻率可以得到單個具有代表性的設定地震事件(M,R)，基于這個設定地震事件來構建的條件目標譜就是“粗略”條件譜。假設這里的目標地震動強度指標為周期T*處的譜加速度，Sa(T*)。使用譜加速度的地震動衰減關系獲得Sa在所有周期Ti的對數平均值和標準差，表示為μlnSa(M,R,Ti)和σlnSa(M,R,Ti)。我國地震區劃圖采用的地震動衰減關系[22]包括長軸衰減關系和短軸衰減關系，計算的粗略條件譜包括長軸和短軸的計算結果。對于目標譜加速度值Sa(T*)，計算其與目標周期T*處μlnSa(M,R,Ti)的差值ε(T*)。

依據條件概率公式，得到任意周期Ti處的粗略條件反應譜的譜加速度對數值的條件均值μlnSa(Ti)|lnSa(T*)為：

式中：μlnSa(M,R,Ti)和σlnSa(M,R,Ti)為衰減關系給出的周期點Ti的對數均值和對數標準差；ρ(Ti,T*)為兩個周期點Sa值的皮爾遜相關系數，該系數一般利用強震動記錄數據庫進行統計得到。

任意周期Ti處的粗略條件反應譜的譜加速度對數值的條件標準差σlnSa(Ti)|lnSa(T*)為：

在給定設定地震的情況下，多個周期的對數譜加速度值服從多元高斯分布[23]，該分布可通過lnSa值的均值和協方差矩陣確定，協方差矩陣為：

式中：ΣTi,Tj=ρ(Ti,Tj)σlnSa(Ti)σlnSa(Tj)為lnSa在周期Ti和周期Tj間的協方差；p為所計算的周期的個數。條件譜是在給定條件周期T*處譜加速度值下的對數譜加速度值的概率分布，可通過條件均值和條件協方差矩陣來表達，條件均值由式(2)給出，條件協方差矩陣可通過式(5)得出：

式中：Σcross是p×1的向量，表示lnSa在周期Ti和條件周期T*間的協方差，Σcross=[ΣT1,T*ΣT2,T*··· ΣTp,T*]。

2) 銜接三維設定地震的完備條件目標譜構建

在我國第五代地震參數區劃圖中，為了考慮斷層走向的影響，定義了方向性函數來表示不同軸向的概率(如圖2 所示)，結合俞言祥等[22]給出的長短軸衰減關系進行地震動參數計算。三維設定地震解耦結果描述了不同震級-經緯度微元對目標危險性水平的貢獻概率。如果對每一個震級-經緯度微元都進行條件譜的構建，然后，將所在潛源的方向性函數作為概率進行加權組合，最后，通過高斯混合分布就可以得到考慮所有潛源貢獻與方向性概率的完備條件譜。

圖2 潛源走向示意圖Fig.2 Schematic diagram of strike directions of the source area

在目標危險性水平下，假設三維設定地震解耦得到的微元k的貢獻率為Pk，該值基于三維設定地震解耦給出。則通過與微元所在潛源走向的概率相乘，即可得到微元k在走向s上的概率，記作Pk,s。將震級、距離和方位角代入俞言祥的長短軸衰減關系[22]后，則該微元k在走向s下的條件均值μlnSa(Ti)|lnSa(T*),k,s和條件標準差σlnSa(Ti)|lnSa(T*),k,s定義如下：

微元k在各走向s下的條件均值和條件標準差均服從高斯分布(正態分布)，且微元k在各走向s下具有相同的條件標準差：

那么考慮了各個潛源的可能方向后，微元k的條件均值μlnSa(Ti)|lnSa(T*),k和條件標準差σlnSa(Ti)|lnSa(T*),k為：

最后，將所有設定地震微元的條件均值和標準差進行相加后就得到了考慮所有設定地震微元與可能方向性貢獻的完備條件譜，其均值和標準差為：

由于完備條件譜依據高斯混合分布構建，協方差矩陣并沒有解析表達。

1.3 案例城市條件目標譜構建實例

銜接圖2 的二維和三維解耦設定地震解耦結果，采用1.2 節中介紹的構建方法，分別構建50 年超越概率2%下條件周期T*=1.0 s 的粗略條件譜和完備條件譜。其中粗略條件譜分別采用了俞言祥等[22]衰減關系長軸，短軸，以及長短軸平均值三種方式計算。對比粗略條件譜與完備條件譜的條件均值和對數標準差如圖3(a)和圖3(b)所示。

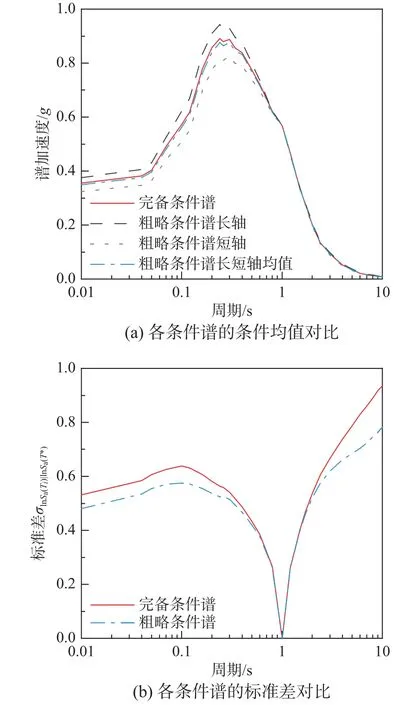
圖3 50 年超越概率2%下，條件周期為1.0 s 的條件譜Fig.3 Condition spectrum with conditional period of 1.0 s under the 50-year excess probability of 2%

從圖3(a)可以看到，完備條件譜的均值介于使用長短軸衰減關系的粗略條件譜的結果之間。圖3(a)的均值譜對比結果表明，就案例城市而言，采用衰減關系長短軸幾何平均值構建的粗略條件譜，相較單獨采用長軸或者短軸的結果要更接近完備條件譜。由于完備條件譜考慮了目標場址周圍潛源所有柵格點的貢獻，而不是單一設定地震，所以其包含了更多潛源信息。但是由于本案例城市的設定地震并不是二極分布類型(即在遠場和近場均存在影響較大的控制潛源或設定地震事件)，所以采用加權平均貢獻設定地震事件得到的粗略條件譜與完備譜基本一致。在進行震級-經緯度三維設定地震解耦比較困難，或者其他構建完備條件譜存在障礙的情況下，可以直接采用這種近似方式來估計條件目標譜的均值。圖3(b)的標準差對比結果表明，完備條件譜的條件標準差要大于粗略條件譜。從式(12)也可以看出，完備條件譜的條件標準差除了包含與粗略條件譜一樣的條件標準差外，還包含了潛源走向不確定性帶來的離散性。值得指出的是，本研究僅考慮了潛源走向的不確定性，當不止一個地震動預測方程通過邏輯樹權重參與了PSHA 計算時，則預測方程的權重需要在高斯混合分布中一并考慮進去。

2 加速度譜相關系數矩陣的區域性影響分析

在上述目標譜構建的過程中的相關系數ρ(Ti,T*)采用了BAKER 和JAYARAM[23]提出的BJ08 模型，此相關模型基于美國西部下一代衰減關系項目(Next Generation Attenuation-west Project, NGAwest)數據庫和衰減關系擬合得到，周期范圍為0.01 s～10.0 s。有學者基于不同的數據集來驗證BJ08相關模型在不同地區的適用性：① JAYARAM等[24]針對日本臺網的記錄(包括俯沖帶地震)；② CIMELLARO[25]使用來自歐洲地震數據庫的記錄；③ DANESHVAR 等[26]使用北美東部的典型記錄；④ JI 等[27]選用了來自中國2007 年-2014 年的強震動記錄數據集，震級從MS5.5 到MS7.0，震中距小于200 km。

圖4 比較了JI 等[27]基于中國2007 年-2014 年地震記錄集的獲得相關系數，基于NGA-west1數據集的BJ08 相關系數，以及基于NGA-west2 數據集擬合的相關系數結果。

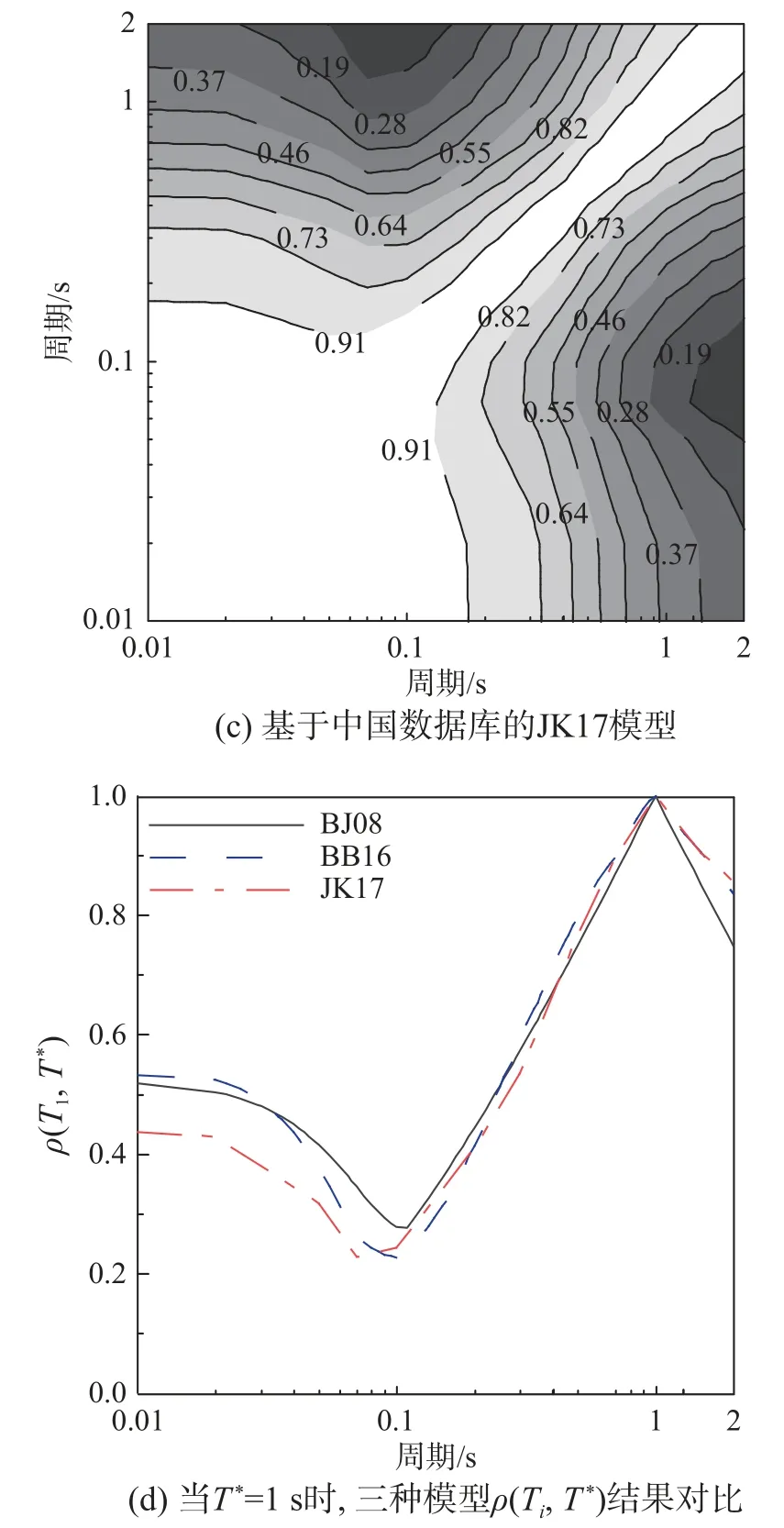
圖4 相關系數對比Fig.4 Comparison of correlation coefficients

比較圖4 中的相關系數結果可知，BAKER等[28]基于NGA-West2 擬合的相關系數結果、JI 等[27]基于中國記錄擬合的相關系數結果和BJ08 相關系數模型趨勢基本一致。當Ti接近Tj時，相關系數ρ(Ti,Tj)接近1；當Ti遠離Tj時，相關系數ρ(Ti,Tj)減小。

為了進一步比較這些結果，圖4(d)給出了條件周期T*=1.0 s 時，基于BJ08、BB16 和JK17 模型預測得到的反應譜相關系數ρ(Ti,T*)。可以看到，相關系數曲線形狀是基本一致的，尤其是在0.1 s～2.0 s 之間，但是在相關系數較低的0.01 s～0.1 s 之間，基于中國數據擬合得到的JK17 模型下的相關系數值是顯著低于其余兩個模型的。以本研究的算例城市為例，分別建立了基于三種不同相關系數模型的條件周期為1.0 s 的完備條件譜和粗略條件譜，其條件均值和對數標準差對比結果見圖5 和圖6。其中粗略條件譜包括基于衰減關系長軸、短軸，以及二者幾何平均值三種目標譜。可以看到，三種相關系數下的完備條件譜、粗略條件譜的條件均值以及條件標準差具有一致的變化趨勢。但是基于我國JK17 模型得到的目標譜在0.5 s 附近區段是高于其他相關系數模型的結果的，條件標準差結果反而要低于其他模型。當選取記錄數據集完全來自中國強震記錄數據庫時，相關系數模型的這一差異是需要考慮的，建議采用基于中國數據擬合的JK17 模型體現中國區域的地震動特征。

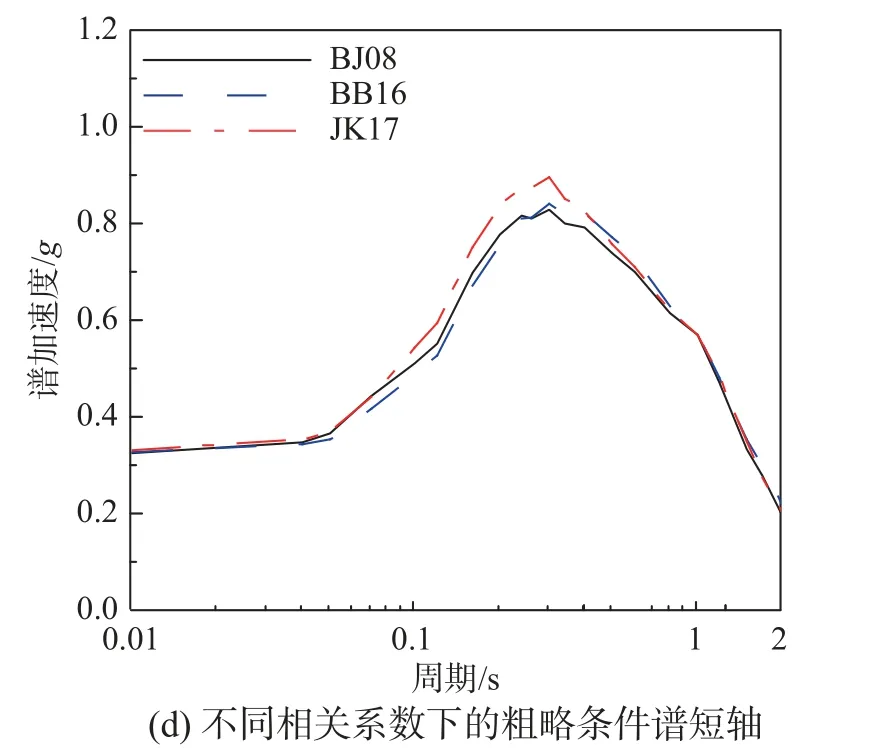
圖5 三種相關系數下周期0 s～2 s 條件均值對比Fig.5 Condition mean spectrum of 0 s～2 s under three kinds of correlation coefficients

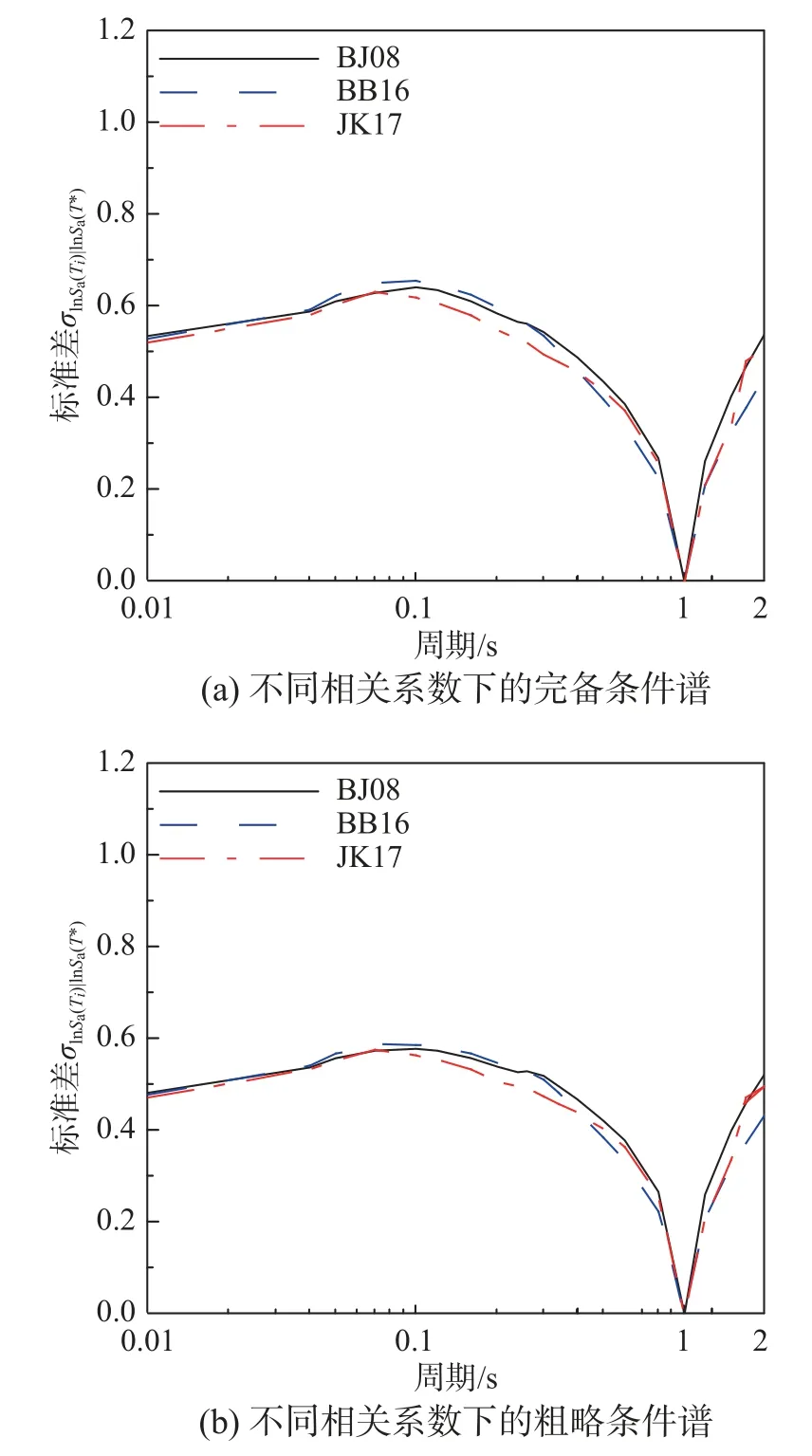
圖6 三種相關系數下周期0 s～2 s 標準差對比Fig.6 Standard deviation of 0 s～2 s under three kinds of correlation coefficients

3 面向完備條件譜的記錄選取方案

和單純的匹配條件目標譜的均值不同，同時匹配目標條件譜分布是一個多維優化問題，即從一個大的記錄數據庫中搜尋N條記錄，使其地震動強度指標(Sa)的分布情況與目標分布一致。對于粗略條件譜來說，其嚴格滿足多元高斯分布，且均值、協方差矩陣都有直接的數學解析表達，因此可以通過拉丁超立方抽樣方法直接得到符合分布的模擬譜。進而通過逐一匹配模擬譜實現最終的記錄選取，采用貪心優化的思路逐一替換模擬譜記錄搜尋具有較好匹配效果的記錄[14]，記錄匹配的思路見圖7 的流程圖。但是作為完備條件譜，其采用了高斯混合分布構造，綜合考慮了目標場址所有潛源設定地震事件的權重，雖然條件均值和條件標準差可以求出解析表達，但是無法直接計算得出協方差矩陣，因而無法直接通過拉丁超立方抽樣得到與選波數量相同的模擬譜作為目標來匹配。

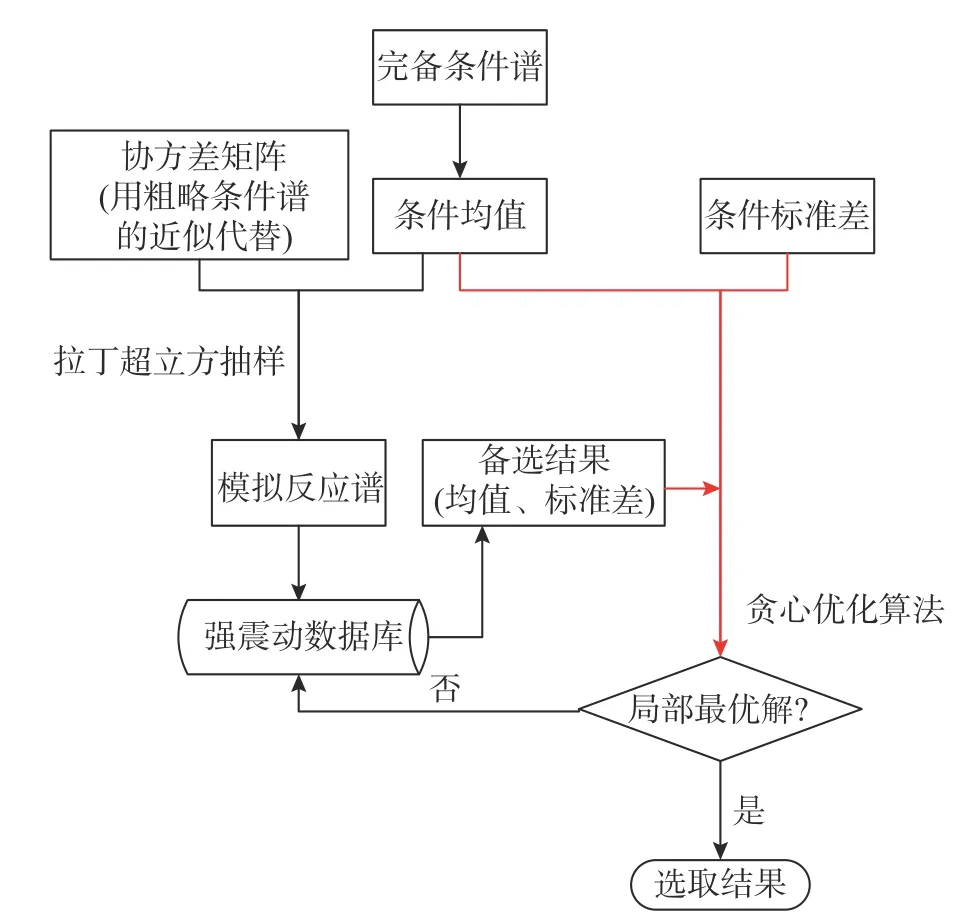
圖7 服從高斯混合分布的完備條件譜的天然地震動記錄選取流程Fig.7 Flow diagram of ground motion selection of exact conditional target spectrum obeying gaussian mixture distribution

BRADLEY[29-30]提出通過兩步蒙特卡羅抽樣的方式來獲得模擬譜：首先，通過潛源微元貢獻率進行蒙特卡羅抽樣得到隨機的潛源微元；然后，計算得到隨機潛源微元下的條件譜作為模擬譜。這樣做雖然可以得到滿足完備條件譜高斯混合分布的結果，但是存在以下弊端：① 由于采用的是蒙特卡羅模擬技術，模擬譜的數量一般需要遠超最終在后續時程分析中用的記錄數量，才可以保證模擬譜的均值與標準差與目標分布一致。由圖8的不同工況下的對比算例可以看到，采用模擬譜的均值和方差與模擬反應譜的條數有很大的關系。當模擬次數達到100 或者更多時，才能得到與目標譜的均值和標準差一致的一組模擬反應譜。同時，由于其基于三維設定地震解耦結果進行模擬譜的構建，當潛源出現二極類型(即近場和遠場同時存在貢獻率較大的設定地震事件)時，會導致模擬譜出現較大偏差，可能出現譜型截然不同的兩簇模擬譜。② 由于記錄選取時并非逐條匹配模擬譜，而是通過匹配地震動強度指標的累積概率分布曲線，因此無法很好地控制最后選取結果的均值和標準差[13]，這會影響后續結構響應的計算結果。

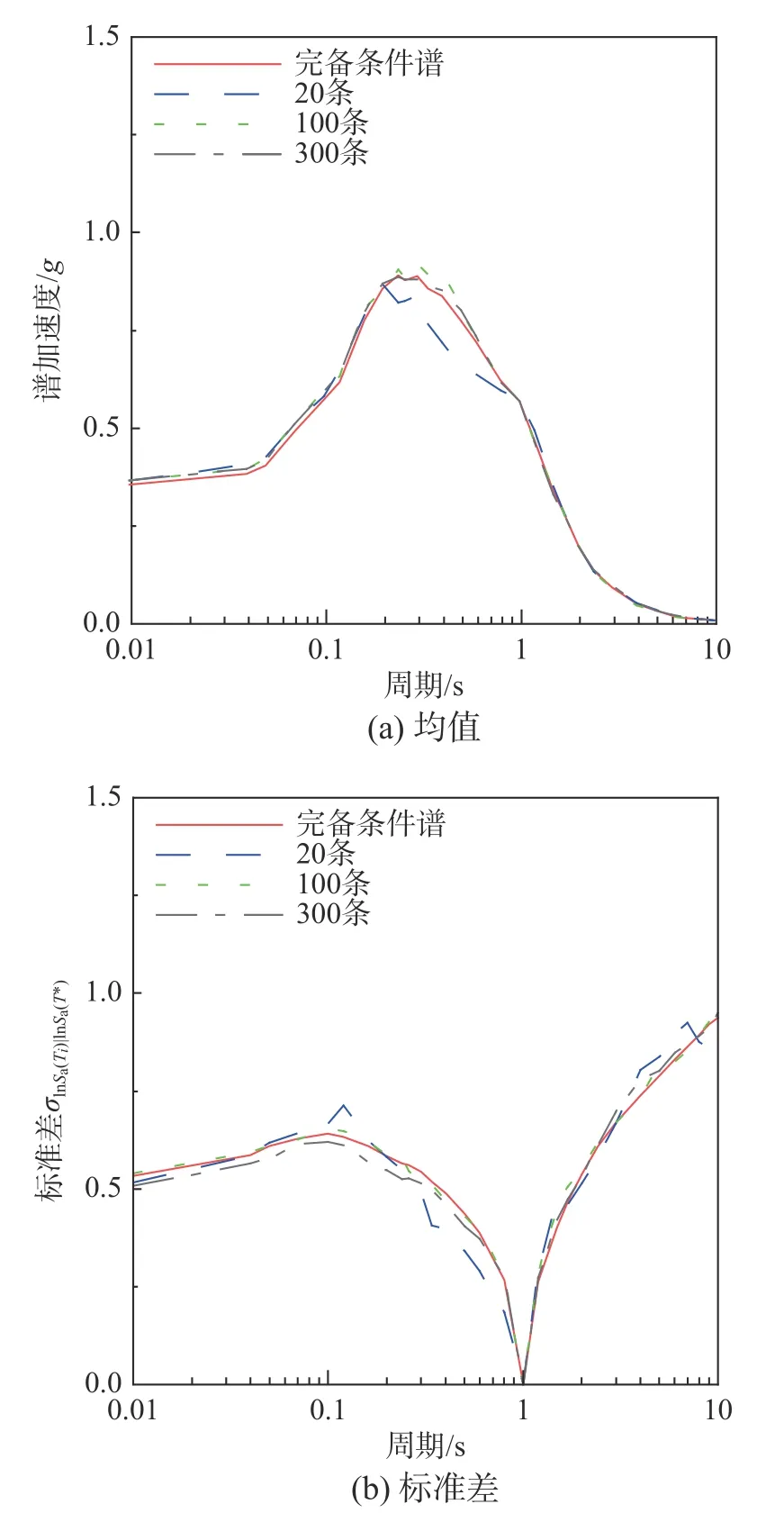
圖8 隨機模擬方法生成不同數量模擬反應譜的均值及標準差Fig.8 Mean and standard deviation of different numbers of simulated response spectra generated by stochastic simulation method

考慮到中國完備條件譜在構建過程中并不涉及多個衰減關系的邏輯權重，且采用的衰減關系本身形式較為簡單，本研究提出一種簡化的匹配思路，即采用多元高斯分布下的協方差矩陣(式(5))來替代沒有解析式的高斯混合分布協方差矩陣，后面就可以直接銜接拉丁超立方抽樣技術來生成與目標記錄選取數量相同的模擬譜，抽樣采用的均值目標譜采用完備條件譜的條件均值(式(11))。簡化算法的計算流程如圖7 所示。這樣做雖然犧牲了協方差矩陣的構造精度，進而導致生成的模擬譜與目標理論分布存在一些差異，但是可以有效避免采用Bradley 兩步蒙特卡羅模擬方法需要生成大量模擬譜才能逼近目標分布的弊端。由圖9的算例可以看出，此方法所得到的模擬反應譜的均值、標準差與完備條件譜的目標基本一致。

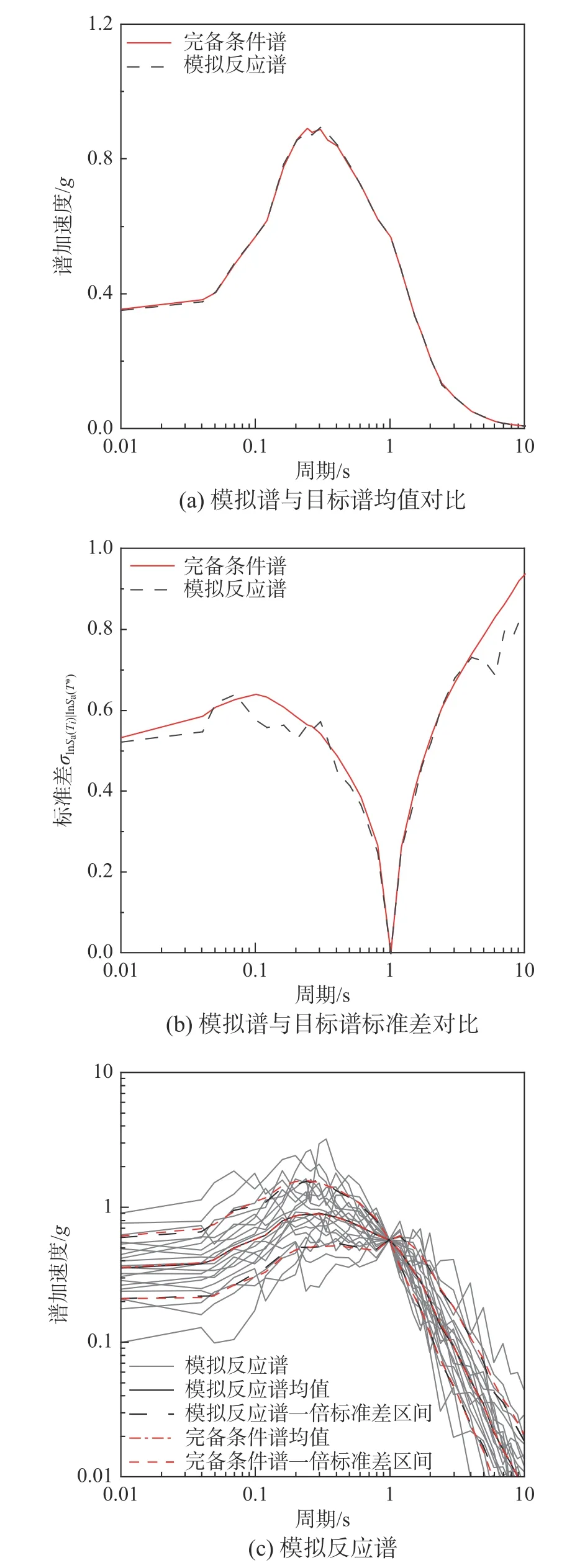
圖9 生成的模擬譜與完備條件譜對比Fig.9 Comparison of the simulated spectrum with exact conditional target spectrum

得到了模擬譜后，就可以采用貪心優化算法[14]做進一步的記錄優選，最終得到滿足條件的強震動記錄集。貪心優化算法的步驟如下，對于模擬反應譜中的每一條反應譜，計算其與強震動記錄庫中的天然地震動記錄反應譜在所考慮的全部周期譜加速度的誤差值之和SSE，從強震記錄數據庫中選取與其最接近的一條，最終獲得一個天然地震動記錄集：

式中：lnSa(Ti)為所選記錄周期Ti處譜加速度的對數值；(Ti)為模擬反應譜在周期Ti處的譜加速度的對數值；p為所考慮的振動周期點的個數；SSE為平方誤差的總和。

當選取的地震動數量較少時，通過最小SSE得到記錄的均值和標準差可能與目標譜略有偏差。因此，使用貪心優化算法來提高所選樣本與目標譜之間的匹配度。貪心優化算法通過在迭代中不斷地量化記錄選取結果與目標之間的誤差來得到一個局部的最優解。在初選得到的樣本中，對每一條地震動進行替換，如果沒有新的地震動使得SSEs改進，則保留樣本中原來所選的地震動。記錄選取結果與目標分布的誤差SSEs如式(14)所示：

式中：SSEs為模擬反應譜與完備條件譜的誤差總和；為選取記錄反應譜周期Ti處譜加速度的對數值的均值；為選取記錄反應譜周期Ti處譜加速度的對數值的標準差；μlnSa(Ti)|lnSa(T*)和σlnSa(Ti)|lnSa(T*)為周期Ti處目標條件譜的均值與條件標準差；w1、w2為控制各IM 指標權重的系數。

采用上述方法，針對前文構建的目標完備目標譜，數據庫為NGA-west1，從7038 條記錄中選取了20 條水平分量天然強震記錄，權重設置為w1=1、w2=2。均值和標準差的匹配結果如圖10 所示。可以看到經過貪心優化算法的優選之后，均值和標準差與目標基本一致，表明實現了較好的匹配效果。但是需要注意的是存在若干條記錄具有較大離散性，該問題可以在記錄選取初期設置上、下限值時進行初步篩選。

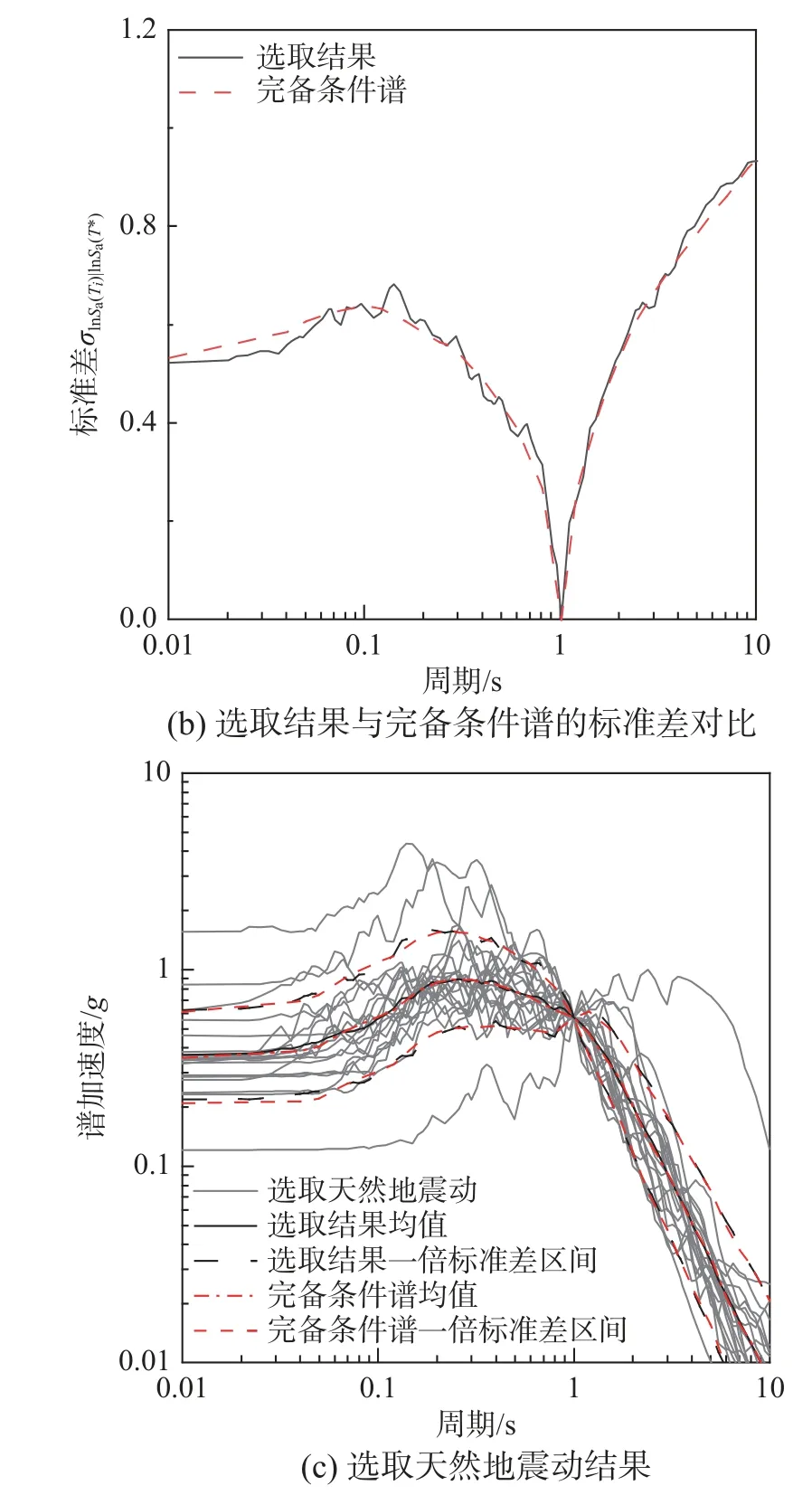
圖10 匹配完備條件譜的天然強震動記錄選取結果Fig.10 Results of selected ground motion matching exact conditional target spectrum

雖然本研究提出的簡化算法可以實現均值與標準差的良好匹配，但仍然需要進一步衡量記錄選取結果的反應譜分布與完備條件譜目標分布之間的差異。Kolmogorov-Smirnov 檢驗方法能夠利用樣本數據，推斷樣本來自的總體是否服從某一理論分布，通過比較選取的天然地震動記錄的多個周期點Sa值的累積經驗概率分布(Cumulative distribution function, CDF)曲線與目標之間的差異判斷所選結果是否可靠。對于所選的天然地震動結果，如果CDF 曲線之間的偏差大于置信區間下的范圍，則認為選取結果不可靠。天然地震動記錄的選取結果在周期0.1 s、0.5 s、2.0 s 和5.0 s 的Sa的CDF 曲線如圖11 所示。可以看出，除了Sa(5.0 s)外，在給定的顯著性水平α=0.1 下，選取結果的Sa值分布基本都落在接受域中。因此，本研究提出的簡化記錄選取算法，雖然并沒有以CDF作為記錄選取的依據，但是同樣實現了與目標分布較好的匹配效果。

圖11 選取結果在周期0.1 s、0.5 s、2.0 s 和5.0 s 與目標分布對比Fig.11 Comparison of the distribution in periods of 0.1 s,0.5 s, 2.0 s and 5.0 s with target

4 結論

本文與我國概率地震危險性分析的設定地震解耦結果相銜接，構造了考慮所有設定地震微元權重和潛源走向的完備條件目標譜，可以為場址危險一致地震動輸入提供記錄選取依據。相關工作與結論如下：

(1) 以北京近郊某城市為算例，構造了粗略條件目標譜與完備條件譜，對比結果表明：完備條件譜的均值介于分別使用長、短軸預測方程的粗略條件目標譜之間；完備條件譜的目標條件標準差要高于粗略條件譜。完備條件譜可以很好地體現潛源的空間分布特征與場址地震危險性之間差異。

(2) 對比了基于不同強震動記錄數據庫擬合得到的加速度反應譜相關系數模型對條件譜構造的影響。對比結果表明，不同相關系數模型下的精確條件譜以及粗略條件譜具有類似的譜型，但是基于我國JK17 模型得到的目標譜在0.5 s 附近區段是要略高于其他相關系數模型的結果的，而條件標準差結果反而要低于其他模型。當后續記錄選取希望準確體現中國區域的地震動特征的時候，相關系數模型的這一差異是需要考慮的，建議采用基于中國數據擬合的JK17 模型計算。

(3) 針對中國完備條件目標譜的構造特點，給出了一種簡化的天然強震動記錄選取方案。采取多元高斯分布的協方差矩陣進行近似替換高斯混合分布的協方差矩陣，結合貪心優化算法進行記錄優選，最終在實現均值、標準差的高效匹配的同時，在Sa指標分布方面也有較好的效果。較好實現了針對中國完備條件譜的記錄選取。