基于LSTM的北斗三號衛星差分碼偏差分析及預測

劉曉文

( 山東廣源巖土工程勘察有限公司, 山東 煙臺 264000 )

0 引言

GNSS差分碼偏差(differential code bias，DCB)，是由不同類型的GNSS信號之間的差異產生的時延差異，按照硬件是設備分為衛星端差分碼偏差和接收機端差分碼偏差，按照頻率相同或不同又分頻內偏差和頻間偏差[1]. DCB作為電離層建模的必須要分離的重要誤差，其精度對電離層總電子含量(total electron content，TEC)具有非常大的影響，嚴重的可以達到30電離層TECU左右的偏差[2]，從而進一步影響到導航定位的精度. 2020年6月，北斗三號(BeiDou-3 Navigation Satellite System，BDS-3)組網成功，BDS-3在繼承北斗二號(BeiDou-2 Navigation Satellite System，BDS-2)的頻率基礎上，增加了兩個新頻點B1C和B2a，且同一頻點具有多個支路，由此產生的新偏差[3].目前能夠連續提供穩定的北斗衛星導航系統(BeiDou Navigation Satellite System，BDS) DCB產品的機構有德國宇航中心(Deutsches Zentrum für Luft- und Raumfahrt，DLR)和中國科學院(Chinese Academy of Science，CAS)，其中DLR采用全球電離層格網模型確定電離層延遲，進而實現DCB參數的確定[4]. 作為電離層的副產品，DCB的精度會受到不同的電離層模型、等效高度、投影函數、插值擬合等因素的影響，太陽活動、地磁活動、天氣環境等因素產生的電離層TEC 變化也會引起DCB的精度和穩定性[5-6]. 在解算DCB參數的時候，通常采用零基準約束進行分離衛星DCB和接收機DCB[7-9]，即所有的衛星或測站DCB為零. 當衛星數目發生改變時，需要重新調整基準，會使得所有DCB參數產生偏差[10-11].

為了解決DLR和CAS發布的DCB產品時延問題、缺失衛星差分碼偏差及其導致的衛星基準變換引起的偏差問題. 本文通過采用機器學習的方法，即長短時記憶(long short-term memory，LSTM)神經網絡來研究和分析BDS-3新頻點長期和短期變化特性，對衛星DCB參數進行預測，以預測值代替真實值，實現了短期預報.

1 BDS-3 DCB 預測方法

1.1 DCB估值基準統一

由于在分離衛星DCB與接收機DCB時，衛星和接收機端DCB線性相關，會造成法方程秩虧[1]，因此我們通常將所有衛星DCB之和約束為0進行參數分離. 當分析一段時間內的DCB值時，可能會存在某幾天的衛星DCB參數缺失或者新的衛星參與計算的情況，會導致基準發生變化，從而使得衛星DCB值產生偏差，因此需要將每一天的基準轉換到統一的基準上面，只有基準統一了才能準確有效的對衛星DCB進行評價. 假設A基準有uA顆衛星，采用所有的衛星DCB和為0，其約束方程為

式中：IuA為系數陣；為A基準下的衛星端DCB參數；uA為衛星數量.

假設統一A基準和B基準，其中A采用了uA顆衛星，B采用了uB顆衛星(uB＜uA)，通常選擇衛星少的一方構建新的基準，即A基準的衛星包含了B基準的衛星，需要將A基準的調整至與B相同的基準.其約束方程有

1.2 多項式擬合法

利用多項式擬合的方式，基于最小二乘法法則，生成N階多項式函數，表達式如下

式中：n為多項式的階數；pn(x) 為擬合出的多項式函數；x為輸入的變量.

通過多項式函數對已有的數據進行擬合或者插值. 本文采用最小二乘法對各衛星頻間偏差參數進行二階多項式擬合，并將擬合出的函數對差分碼偏差預測.

1.3 LSTM神經網絡模型

LSTM是一種時間循環神經網絡，相較于循環神經網絡(recurrent neural network，RNN)，LSTM能夠在長序列訓練當中避免梯度消失和梯度爆炸的問題[12-13]. LSTM模型神經元結構如圖1所示.

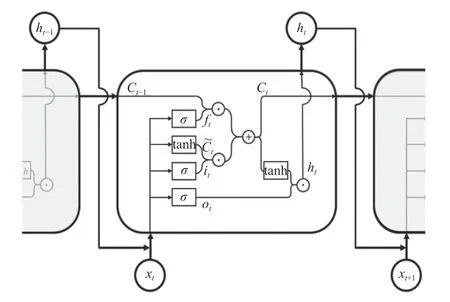
圖1 LSTM神經網絡的內部結構

LSTM 神經網絡單元通過遺忘門、輸入門和輸出門來替換原有的RNN神經網絡單元，而LSTM之所以能夠解決RNN的長期依賴問題，是因為LSTM引入了門(gate)機制用于控制特征的流通和損失[14-16].遺忘門決定了上一時刻的細胞狀態ct-1中的那些信息被遺忘，遺忘門ft公式為

在輸入門中，激活函數使用了 tanh 函數來進行更新當前時刻的單元狀態，再通過遺忘門留下的信息ft、上一時刻的信息Ct-1和更新后的候選值得到新的值，從而實現了當前記憶和長期記憶的結合[17]. 具體公式為

式中：it為輸入門輸出；wi為輸入門的權重；bi為輸入門的偏置項；C為候選信息；wC為候選單元的權重；bC為候選單元的偏置項；Ct為得到的新單元的信息；其余參數同式(5).

在輸出門中的輸出ot和t時刻單元的輸出ht公式如下：

式中：wo為輸出門的權重；bo為輸出門的偏置項.

通過對大量樣本數據的學習，反復更新LSTM內部的權陣以及參數，即可完成LSTM的訓練，從而實現對數據進行分類、預測等處理.

1.4 評價指標

為了有效的評價LSTM神經網絡的預測效果，本文將預測出來的結果與CAS發布的值進行比較，并采用平均絕對誤差(mean absolute deviation，MAE)、均方根誤差(root mean squared error，RMSE)和精確度P三個性能指標來評估模型的性能. 三個性能指標[17]的定義分別為：

2 數據處理與結果分析

2.1 太陽風暴以及地磁指數分析

2020年6月23日之后BDS-3正式開通，時至2021年底組網完成僅一年半左右的時間，因此本文選取采用的是德國地學中心(Helmholtz-Centre Potsdam-German Research Centre for Geosciences，GFZ)

發布的2021年的太陽輻射指數數據和地磁指數數據進行分析[18]. 表1和表2為太陽輻射通量和地磁指數AP指數的等級劃分，圖2表示太陽輻射指數F10.7和平均地磁AP指數的2021年的時間變化序列，由圖2可知，太陽活動水平和地磁擾動強度都處于比較活躍的狀態，其中太陽輻射通量幅值有116 d大于90 d，地磁指數幅值有137 d大于7 d，這表明地球磁場處于擾動和活躍狀態. 尤其是在下半年，太陽輻射通量和地磁指數都發生比較大的變化，其中在2021年5月13日和11月4至5日發生了大地磁暴事件. 這意味著電離層同樣也會產生比較大的擾動.與此同時，對于北斗衛星的DCB產品的穩定性會產生一定的影響，因此如何準確的預報的帶衛星的DCB在不同空間天氣狀態下的是非常有必要的.

表1 太陽輻射通量等級劃分

表2 地磁活動AP指數等級劃分

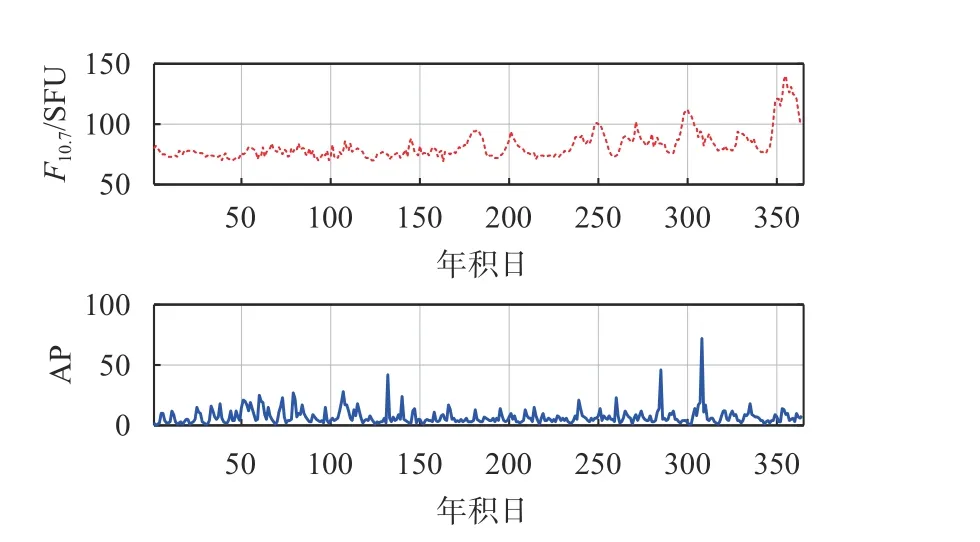
圖2 2021年太陽輻射通量F10.7和地磁指數AP時序變化

2.2 BDS-3 DCB時序分析

CAS發布的DCB產品包括八種，本文主要對BDS-3新信號的C1X-C5X，C1X-C6I，C1X-C7Z，C1XC8X四個頻間偏差進行分析. 本文選取的是CAS發布的2021年的年積日001—359中BDS-3未發生跳變時的DCB日產品，其時間序列繪圖如圖3所示. 不難看出，大部分時間BDS-3 DCB值變化不大，都在±0.3 ns內. 但是當衛星數目發生變化的時候，由于約束條件發生了改變，衛星DCB的值會出現較大的波動. 這是由于在分離衛星和接收機端的DCB，通常采用“零均值”約束，即所有衛星端的DCB之和為0[19-20]. 不同時間的DCB會受到衛星數量變化的影響，當某一天的衛星由于一些原因不參與解算而舍棄時，其衛星約束基準會發生變化，因此需要將不同時間的DCB的基準進行統一. 重新實現零基準繼續約束后，將其中缺失的衛星DCB值被看作0，實際上這樣的值是不符合邏輯的和實際情況的，會對導航定位產生較大的誤差. 因此在衛星未出現失效、更新和加入新的衛星時，實現對已有產品中缺失的情況進行改進，精確估計缺失的衛星DCB值，具有重要意義.

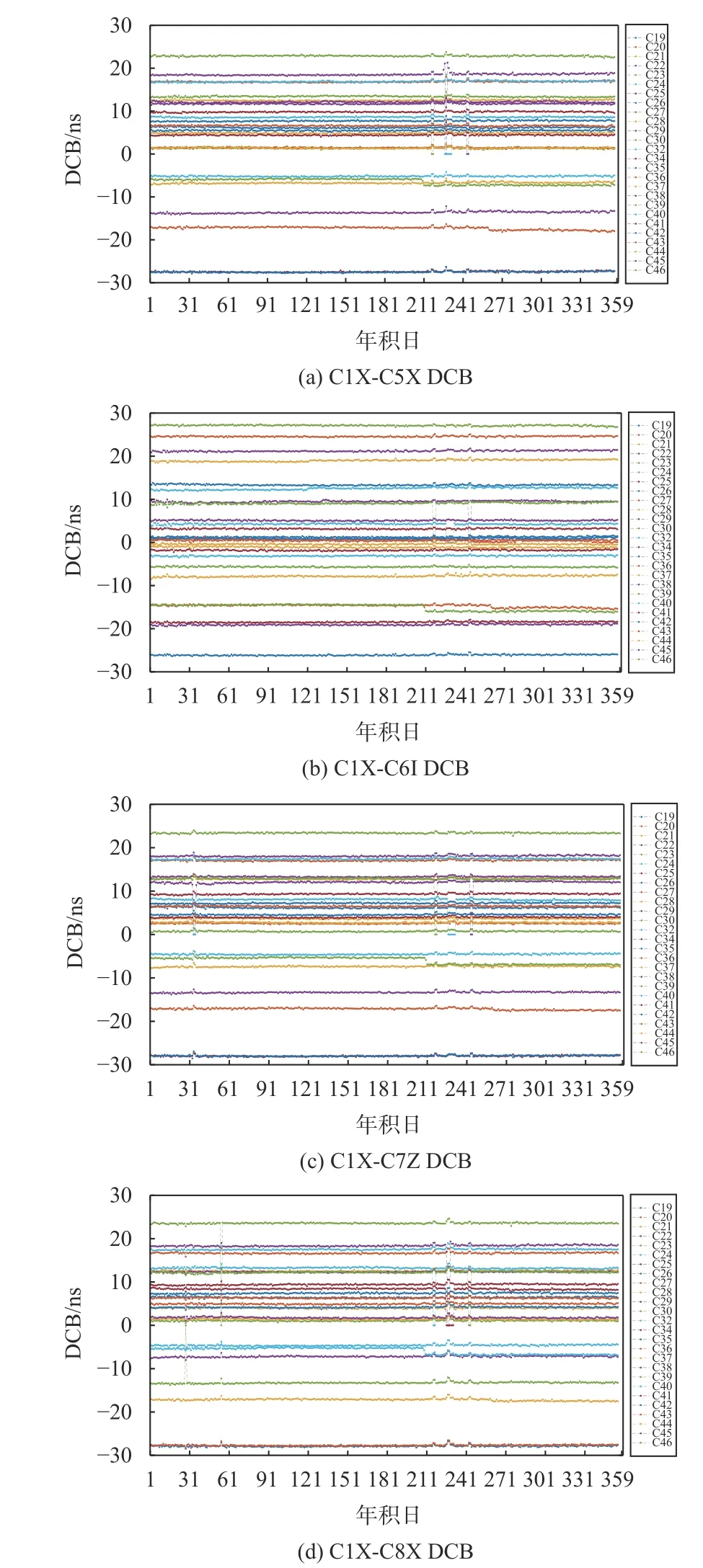
圖3 2021年的年積日001—359 BDS-3 DCB的時間序列

2.3 BDS-3DCB的預測

2.3.1 LSTM-多項式插值法

為了分析LSTM神經網絡的預測效果，本文以BDS-3 C1X-C7Z頻間偏差為例. 以2021年年積日001—310 d的CAS發布的DCB產品和GFZ發布的太陽輻射通量和地磁指數作為實驗數據. 因此需要設置兩個輸入層，設置5個隱含層和1個輸出層，訓練次數選擇100次，采用自適應學習率，其中選取310 d的數據作為訓練樣本，預測7 d的數據并將與多項式預測模型進行對比.

由圖4和圖5可知，LSTM和多項式擬合法兩種模型對BDS-3 DCB的預測都有比較好的效果，MAE均小于0.2 ns，RMSE均小于0.5 ns. LSTM神經網絡的預測效果總體要優于多項式擬合法，LSTM的MAE相較多項式擬合法要小約0.04 ns，RMSE要小約0.22 ns. 傾斜地球同步軌道(inclined geosynchronous orbit，IGSO)衛星的誤差相較于中地球軌道(medium earth orbit，MEO)衛星保持在比較低的水平上，這是由于訓練的樣本的值較為穩定，此外還應該得益于IGSO衛星的信號抗干擾遮擋能力強、穩定性最好的結果.

圖4 LSTM預測結果與多項式擬合法預測結果MAE比較

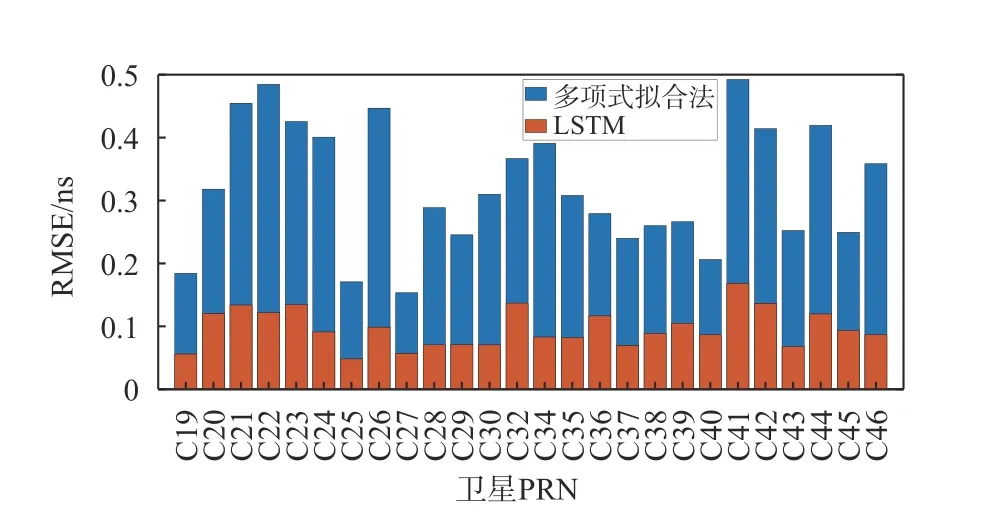
圖5 LSTM預測結果與多項式擬合法預測結果RMSE比較

2.3.2 不同時長的LSTM預測

此外為了進一步驗證時間對LSTM神經網絡的預測效果影響，本文調整預測時長，分別預測7 d、15 d和30 d衛星DCB值，圖6為使用LSTM神經網絡進行預測7 d、15 d和30 d的MAE和RMSE. 由圖6可知，不同天數的預報效果，MAE均小于0.15 ns，RMSE小于0.2 ns，其誤差并沒有隨著天數的增加而發生較大的變動. 其中IGSO衛星的預測效果較其他衛星相對穩定. C41號衛星的預測誤差較大，效果相對不理想，圖3時間序列中可以看到C41號衛星DCB的值相對較大，在27 ns左右，其數值變化較其他衛星較大，因此在預測時的效果相對較弱. 訓練樣本的差異過大對未來的數值進行預測時會同樣會產生較大誤差，因此訓練樣本的穩定性也會預測效果產生比較大影響.

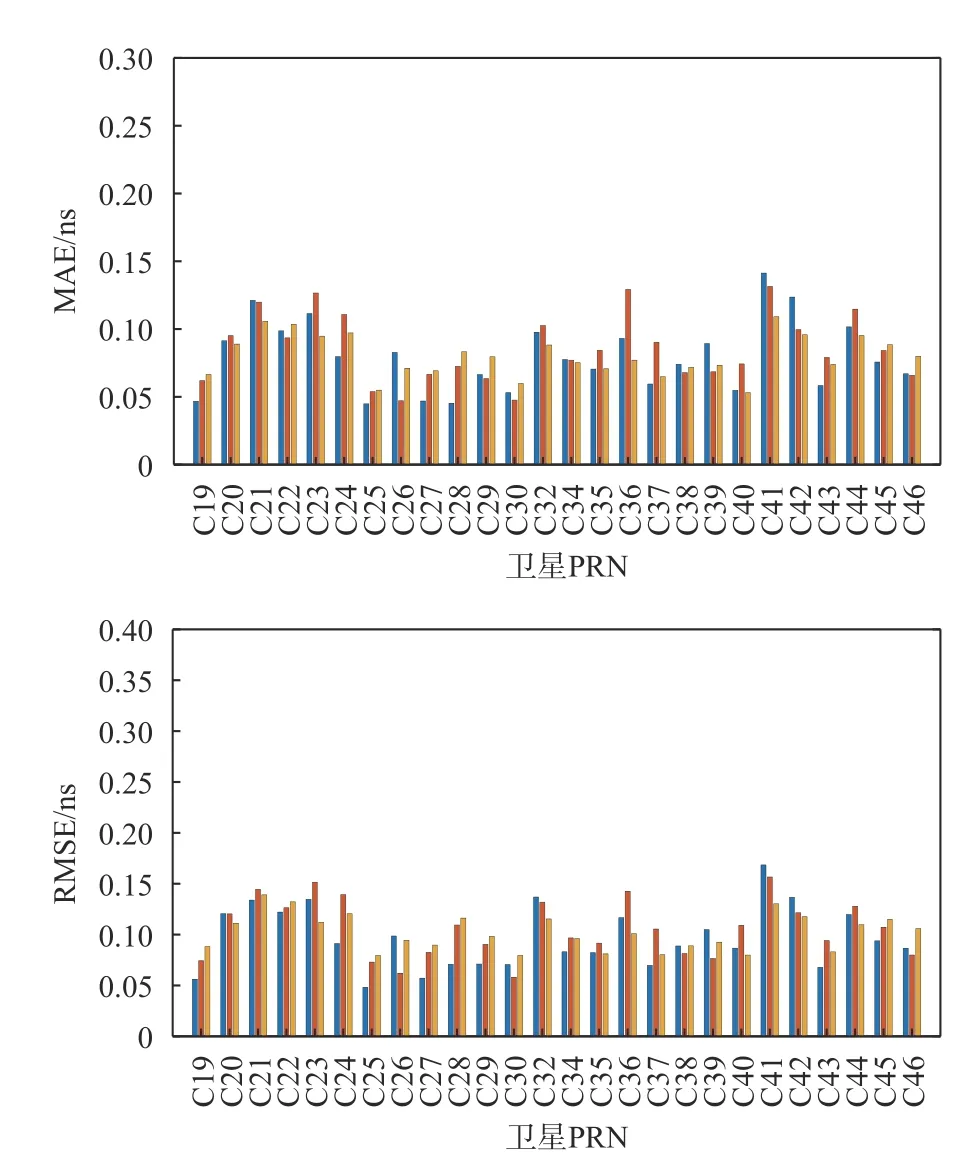
圖6 LSTM模型預報不同天數結果對比

選取BDS-3中MEO衛星C25、IGSO衛星C40的四個頻率不同天的預測結果進行對比，其精確度結果如表3所示. 可以看到相同頻率下，IGSO衛星的精確度較MEO衛星稍低，但精確度均保持在95%以上；不同天數的預測精確度相似，較為穩定. 同一衛星的不同頻率的精確度相差較小. 總上所述，LSTM對于不同衛星軌道，不同頻率的DCB均有較高的預測精度.

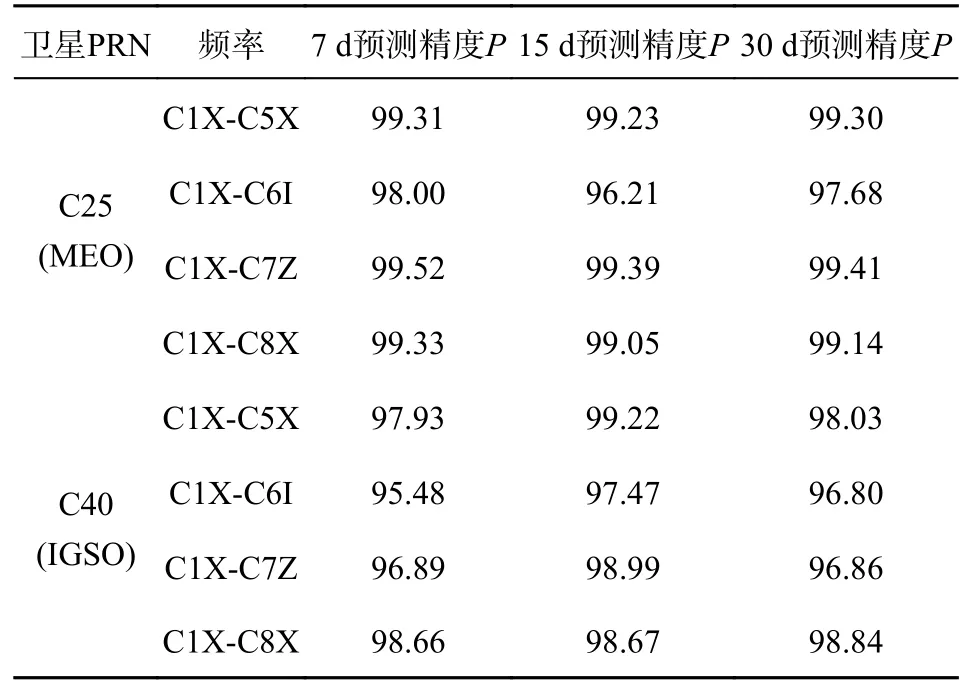
表3 不同軌道衛星DCB預測精度對比%

3 結束語

本文通過CAS發布的2021年的年積日001—310 d的DCB產品作為訓練樣本，采用LSTM神經網絡BDS-3 DCB進行預報和分析. 實驗結果表明，通過LSTM神經網絡進行預測，效果優于多項式擬合的方法，可以有效的對衛星DCB實現多天的預測. 盡管2021年太陽和地球磁場都比較活躍，LSTM神經網絡模型對衛星DCB仍然可以實現比較好的預測效果. 當衛星DCB產品缺失，基準發生改變而引起的DCB值得波動時，LSTM神經網絡預測的結果與CAS發布的產品值的MAE與RMSE均保持較低的水平，擬合效果精度高.