顆粒間碰撞對槽道湍流中顆粒聚集效應的影響研究1)

崔元凱 張 歡

(蘭州大學湍流-顆粒研究中心,蘭州 730000)

(蘭州大學西部災害與環境力學教育部重點實驗室,蘭州 730000)

(蘭州大學土木工程與力學學院,蘭州 730000)

引言

顆粒兩相湍流,即攜帶有慣性顆粒 (響應時間不為0 的顆粒) 的湍流,廣泛存在于自然現象和工業界中.例如,沙塵暴、暴風雪、火山噴發等自然現象[1-3],以及工業界的流化床和顆粒的起動傳輸等[4].這些流動展現出極度的復雜性,主要體現在超高的流動雷諾數[5-6],湍流、顆粒、電場之間的多場強耦合作用[7],以及在大量控制參數中反映出的巨大尺度差異等[8],使得這些顆粒兩相湍流的研究對研究人員構成了巨大挑戰.

已有絕大多數研究主要關注攜帶單分散顆粒的兩相湍流.然而,在幾乎所有實際系統中,例如自然界中的沙塵暴[9]以及工業中的流化床[4]等,顆粒都是多分散的.通常情況下,在沙塵暴等自然系統中,由于顆粒的體積分數較低,通常僅發生顆粒的二元碰撞.而且顆粒在流體中的混合和分散通常通過考慮顆粒對的相對運動來進行分析.因此,在這種情況下,多分散顆粒兩相湍流可簡化為雙分散體系[10].

目前,顆粒兩相流的研究手段主要為實驗測量和數值模擬.多數實驗測量基于粒子圖像測速法(particle image velocimetry,PIV) 或粒子追蹤測速法(particle tracking velocimetry,PTV) 分別獲得粒子場(包含連續相的示蹤粒子和分散相) 的歐拉信息和拉格朗日信息[8].當前直接數值模擬主要分為顆粒分辨直接數值模擬 (particle-resolved direct numerical simulations,PR-DNS) 和點顆粒直接數值模擬 (pointparticle direct numerical simulations,PP-DNS)[11].PRDNS 采用浸入邊界法和直接力法等完全解析顆粒周圍流動的細節.當顆粒小于湍流的最小尺度,PPDNS 將每個顆粒視為流動中的一個點,并通過理論模型或經驗關系確定顆粒所受的流體力.基于以上方法,國內學者在顆粒兩相湍流研究中做出了突出貢獻.例如,Zheng 等[12]開創性地在蘭州大學多功能環境風洞實驗室,使用PIV/PTV同步測量了流場和顆粒相,開展了風洞底部直接起沙和風洞頂部投沙兩種情況下顆粒-壁面過程對流場超大尺度結構的影響研究.結果表明在沒有顆粒-壁面過程的區域,顆粒的存在可以增大超大尺度結構,而在具有顆粒-壁面過程的區域,超大尺度結構的尺寸會顯著減小甚至破壞.Li 等[13]在摩擦雷諾數為430 的水平槽道中進行了氣固兩相流的PIV 測量.該研究發現,顆粒增強 (減弱) 流場內區 (外區) 速度脈動,同時減小近壁流向渦結構的尺度.Wang 等[14]提出了一種新的流體動力應力模型,可以準確重建作用在浸沒單元上的力,可用于模擬有限尺寸顆粒在湍流中的相互作用.數值結果表明,該模型在邊界層內大約需要一個或兩個網格點來準確重構流體力學力分布,顯著降低了解析顆粒周圍流場的成本.Jie 等[15]使用PP-DNS 模擬了摩擦雷諾數600～ 2000 的顆粒兩相槽道流,揭示了在高雷諾數下形成的多尺度顆粒近壁條帶結構.Li 等[16]使用PP-DNS 研究了慣性顆粒對平板發展湍流邊界層調制的影響.他們發現顆粒-流體相互作用導致額外的能量耗散,這在湍流調制中起著關鍵作用.Shao 等[17]提出了一種基于虛擬區域的直接力方法,對水平顆粒槽道湍流進行了全面解析的數值模擬.結果表明當顆粒沉降效應可以忽略時,顆粒的存在通過削弱大尺度流向渦旋的強度減小靠近壁面的流向速度脈動的最大均方根值;當顆粒沉降效應顯著時,大多數顆粒沉降到底壁形成顆粒沉積層并起到粗糙壁的作用,從沉積層脫落的部分渦旋結構上升到核心區域,顯著增加了該處的湍流強度.

實驗測量和數值模擬均表明在顆粒兩相壁面湍流中,顆粒有向壁面 (即湍流強度的負梯度方向)遷移的趨勢,導致顆粒的平均濃度在黏性底層內出現峰值,該現象被稱為湍泳 (turbophoresis).這是由Caporaloni 等[18]和Reeks[19]在同一時期發現的.當顆粒對湍流響應的時間尺度與湍流緩沖層的特征時間尺度相匹配時,湍泳現象被證實是最顯著的[20].另一方面,慣性顆粒通常傾向于優先聚集在近壁的低速區 (即瞬時速度低于平均速度的區域),被稱為傾向性或優先聚集 (preferential concentration),從而形成條帶狀的顆粒團聚[21].通常,當顆粒對湍流響應的時間為湍流的最小時間尺度 (即Kolmogorov 時間尺度) 的量級時,這種條帶狀的團聚是最明顯的.然而,對于小慣性和大慣性的顆粒 (即顆粒響應時間尺度遠小于或大于Kolmogorov 時間尺度),它們不能形成團聚,因為前者完全跟隨流體,而后者的運動幾乎與流動完全無關.

上述現象均局限于顆粒間的碰撞 (即顆粒-顆粒碰撞) 可忽略的情形,可以預見,當顆粒間的碰撞較為顯著時顆粒的聚集行為會被改變,但其具體規律尚不完全清楚.例如,Wang 等[22]通過顆粒兩相均勻各向同性湍流的直接數值模擬發現,顆粒間的碰撞概率受到兩種機制的影響,即引起顆粒間相對運動的湍流脈動 (湍流輸運效應) 和導致平均碰撞概率額外增強的傾向性聚集效應 (因為引起了較高的顆粒局部濃度).同時,Yamamoto 等[23]通過顆粒兩相豎直槽道湍流的大渦模擬研究發現,顆粒間的碰撞促進了顆粒的橫向混合,混合效應使得顆粒速度和顆粒濃度的分布即使在非常稀薄的條件下 (顆粒體積分數～ 10-4) 也變得更加平坦.考慮了顆粒間碰撞的數值結果比沒有碰撞的結果更好地接近實驗結果,因此顆粒間碰撞是不容忽視的.他們進一步通過可視化瞬時流場的空間結構發現,在忽略顆粒間碰撞的情況下,小斯托克斯數顆粒受湍流結構影響,形成了顆粒云 (即傾向性聚集).然而,一旦顆粒云形成,單向耦合和雙向耦合的結果會有所不同,因為顆粒云會影響湍流結構.顆粒間碰撞引起顆粒在橫向方向上的分布更加分散,導致有和無碰撞的與壁面平行的平面上顆粒分布結構在近壁區存在很大的差異.通過考慮顆粒間碰撞,所觀察到的槽道中心區域的顆粒云形狀和尺度與實驗觀測非常吻合,因此顆粒間碰撞極大地影響了顆粒的傾向性聚集效應.總之,顆粒間碰撞對顆粒分布和聚集的顯著影響已經被廣泛地證實,然而已有結果大多針對均勻各向同性湍流或采用大渦模擬手段,尚缺少關于顆粒兩相槽道湍流的直接數值模擬研究,顆粒間碰撞對顆粒聚集程度和形態影響的定量規律仍不清楚.

本文基于歐拉-拉格朗日點顆粒框架,在摩擦雷諾數為Reτ=180 的條件下,采用PP-DNS方法探討了有/無顆粒間碰撞時水平槽道湍流中雙分散顆粒聚集程度和聚集模式的差異.算例的顆粒平均體積分數設置為,此時顆粒間的碰撞不可忽略,其對應的顆粒平均質量分數為～O(1),因此模型中還考慮了顆粒對流場的反饋.

1 數值方法

1.1 控制方程

本文基于歐拉-拉格朗日點顆粒框架,采用湍流-顆粒雙向耦合模型模擬顆粒兩相水平槽道湍流.我們考慮的是懸浮的顆粒,其直徑遠小于湍流的Kolmogorov 尺度,此時不可壓縮的牛頓載流體受質量和動量平衡方程的控制[24-26]

其中,u=(u,v,w) 為流體速度,x=(x,y,z) 為空間坐標;u,v,w和x,y,z分別代表流向、壁法向和展向的速度和坐標.此外,t為物理時間,ρf為流體密度,p為壓強,ν 為流體運動黏度.附加源項f代表顆粒對流體的反饋作用,可以表示為[26]

對于顆粒相,本文考慮的是懸浮在槽道湍流中的剛性的球形顆粒.顆粒密度比 ρp/ρf?1,因此點顆粒的近似是相當合理的,且斯托克斯拖曳力在流體對顆粒的作用中占主導[28-29].與眾多研究一樣,為了突出顆粒慣性的影響,本文不考慮顆粒的重力沉降[15,24-26].因此,在拉格朗日描述中每個顆粒被單獨地跟蹤

顆粒動力學行為受無量綱參數-黏性(或Kolmogorov)斯托克斯數S t+=τp/τν(或S tk=τp/τη)控制,它被定義為顆粒慣性響應時間 τp與黏性時間尺度 τν(或Kolmogorov 時間尺度 τη) 的比值.該參數權衡了顆粒慣性的重要性.當斯托克斯數遠大于1 時,顆粒將如彈道般運動,但當斯托克斯數遠小于1 時,顆粒將跟隨流體運動[32].

除了顆粒與壁面的碰撞,我們還考慮了顆粒間的碰撞,這是因為顆粒的傾向性聚集和湍泳導致了非常高的局部顆粒濃度[22-23].顆粒-壁面和顆粒間的碰撞包含了完全彈性和非完全彈性碰撞兩種情形,并使用“硬球”模型進行描述 (即不計算顆粒的碰撞過程),這與大量已有的研究一致[26,32-33].由于顆粒相是稀疏的,只涉及顆粒間的二元碰撞.因此,考慮兩個標記為1 和2,速度為up,1和up,2的顆粒相互碰撞,顆粒1 碰撞后速度由以下公式給出

其中,mp,1和mp,2分別是顆粒1 和2 的質量;e是碰撞恢復系數,其定義為碰撞前后兩顆粒沿接觸點法線方向上的分離速度與接近速度之比.顆粒2 碰撞后的速度可通過指數1 和2 的互換得到.

本文的槽道湍流是由均勻壓力梯度驅動的,從而保持恒定的體平均速度.無量綱控制參數摩擦雷諾數定義為Reτ=uτδ/ν,其中uτ是摩擦速度,δ 是半槽高度.在本文中,上標“+”表示以黏性尺度為單位進行度量的物理量.水平方向 (即流向和展向) 采用周期性邊界條件,壁面為無滑移邊界條件.類似地,對水平方向上的顆粒施加周期性邊界條件,而對頂部和底部壁面上的顆粒施加反射性的邊界條件 (即顆粒的流向和展向速度不變,壁法向速度等值反向).顆粒間的碰撞是通過基于歐拉網格的方法來檢測的,其中潛在的碰撞顆粒對是在目標及其鄰近單元中被搜索的[34].

1.2 模擬設置

本文所有的模擬均在摩擦雷諾數Reτ=180 下進行,計算域大小為Lx×Ly×Lz=2πδ×2δ×πδ,其中半槽高度 δ=1 m .計算域被離散為Nx×Ny×Nz=256×192×128個網格點,網格在水平方向上是均勻的(即網格流向間距 Δ和展向間距 Δ約為4.42),但在壁法向被拉伸加密 (因此壁法向網格間距 Δ大約在0.52～2.46 的范圍內).詳細的網格參數請見表1.圖1 描繪了本文模擬的示意圖,其中灰色 (黑色) 圓球表示了小 (大) 顆粒的瞬時位置 (僅yp＜0.5 m 且每300 個顆粒被顯示),下壁面附著的湍流漩渦通過Q準則展示 (Q=0.6 等值面),且用u′+染色.上下邊界為流體無滑移和顆粒反射的壁面,水平方向的流體和顆粒均為周期邊界條件.

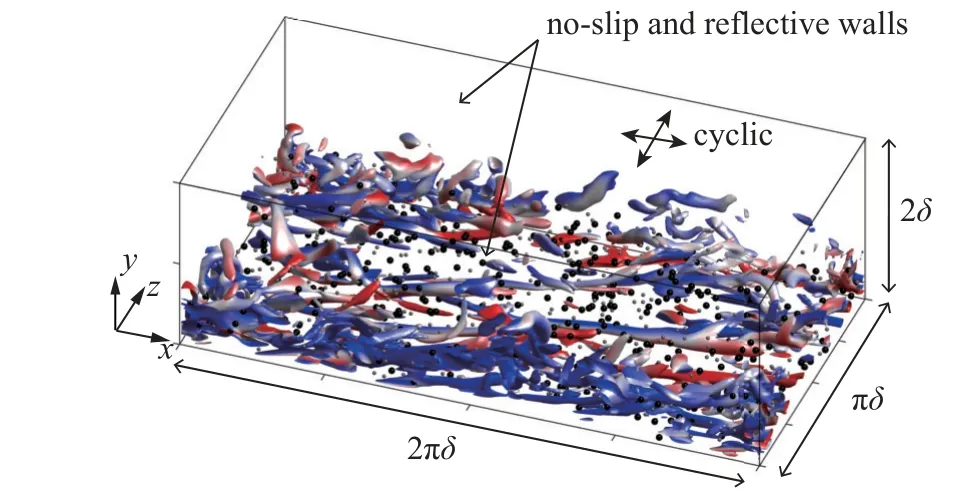
圖1 直接數值模擬的計算域和邊界條件示意圖: 其中流場和顆粒相在流向和展向為周期 (cyclic) 邊界條件,而在上下壁面分別為無滑移(no-slip) 和反射 (reflective) 邊界條件Fig.1 Schematic diagram of the computational domain and boundary conditions for direct numerical simulation: the flow field and particulate phase have cyclic boundary conditions in the streamwise and spanwise directions,while the upper and lower walls have no-slip and reflective boundary conditions respectively

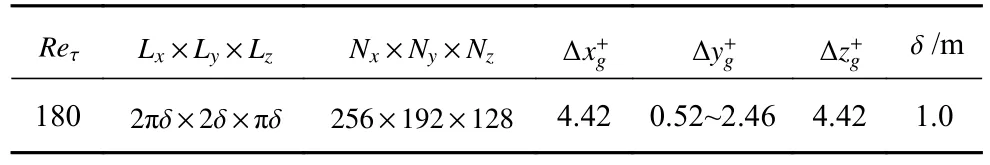
表1 DNS 的網格參數Table 1 Grid parameters of DNS

本文考慮了攜帶雙分散顆粒的水平槽道湍流,總共設置了5 個算例,如表2 所示.算例I 為單相槽道湍流 (single-phase flow),通過將其與標準湍流數據集對比完成程序的驗證,如圖2 所示.在圖2 中,線條表示本文的計算結果,而符號表示Lee 等[35]的模擬結果.平均流向速度和速度脈動均方根都吻合較好,確保了本文的數值模型能很好地再現槽道湍流.算例II 和III 分別為考慮完全彈性顆粒間碰撞和不考慮顆粒間碰撞 (without coll.) 的顆粒兩相流.算例Ⅳ和Ⅴ為恢復系數e=0.8 和e=0.6 的非完全彈性碰撞的情況.在本文中,我們考察了兩種類型的顆粒,即St+=20 的小顆粒和St+=60 的大顆粒.與之對應的Kolmogorov 斯托克斯數Stk在壁面處最大 (小顆粒S tk=4.48,大顆粒Stk=13.4) 而在槽道中心處最小 (小顆粒Stk=1.03,大顆粒S tk=3.11).兩種顆粒的數目被平均分配,即每種5×105個.顆粒與流體的密度比與自然界中沙粒與空氣的密度比相同,即ρp/ρf=2200,因此小顆粒的直徑為=0.4 (dp=2.2 mm),大顆粒的直徑為=0.7 (dp=3.8 mm),均小于流場的Kolmogorov 尺度,保證了點顆粒方法的適用性[36].

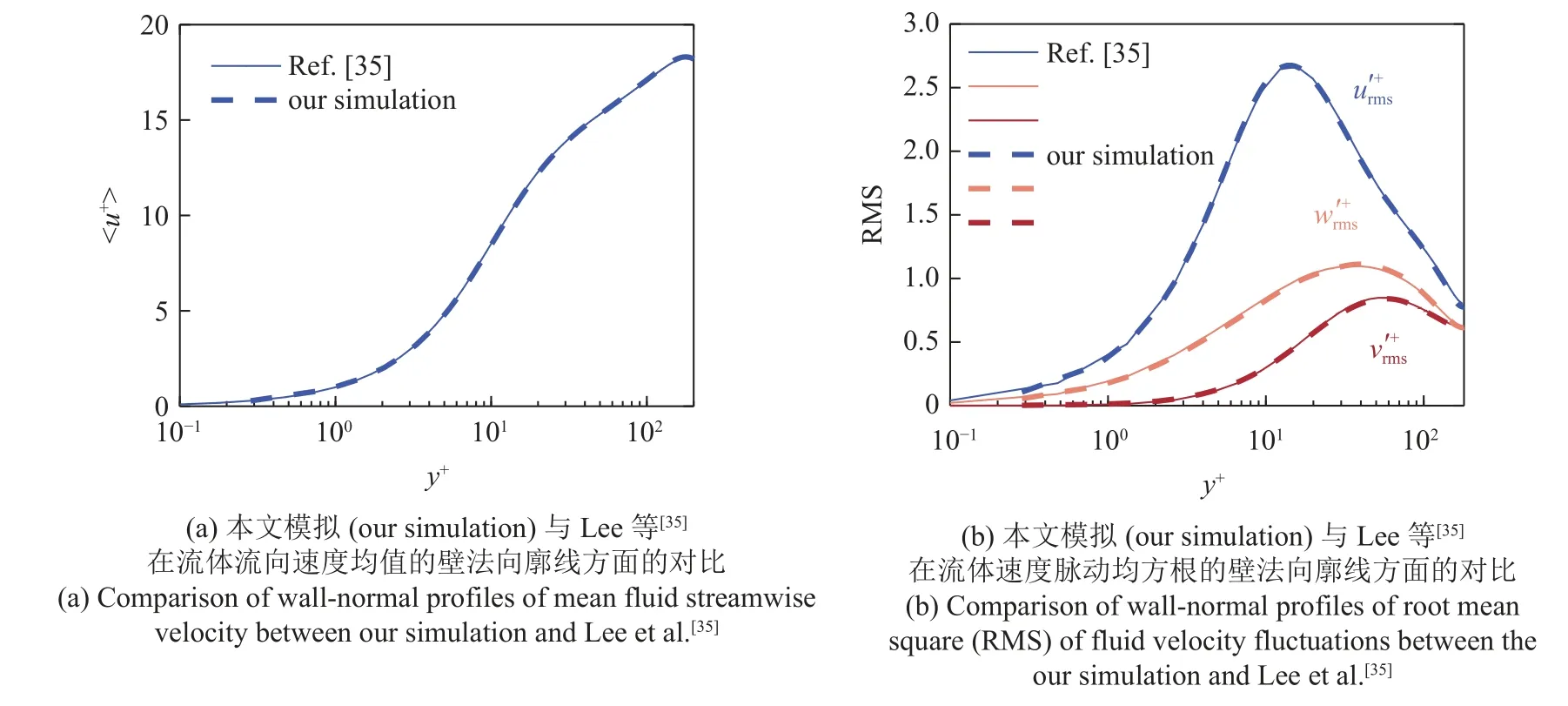
圖2 數值程序的驗證Fig.2 Verification of the numerical program

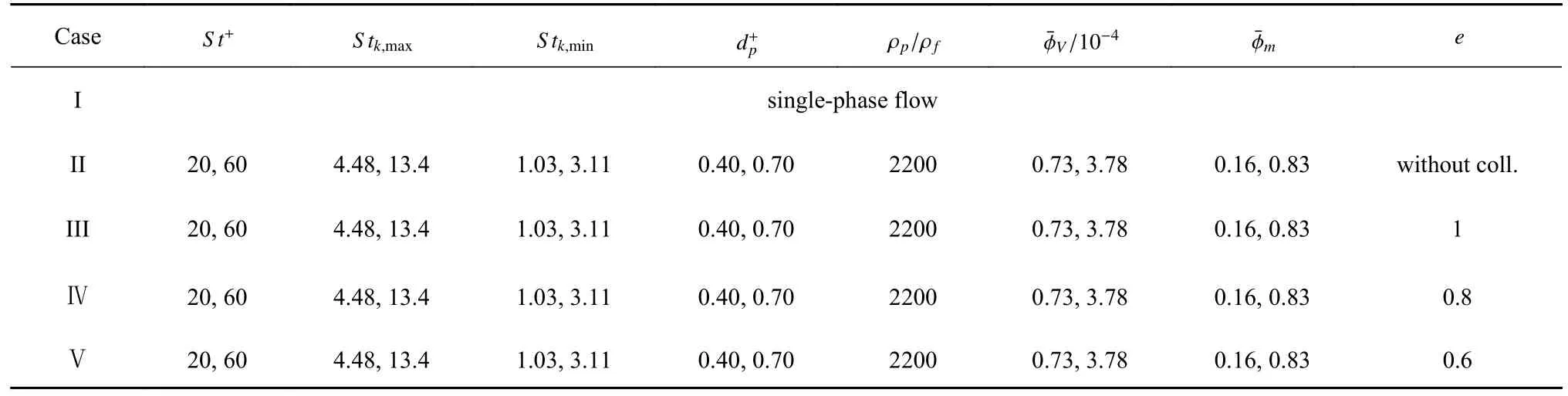
表2 算例設置匯總Table 2 Summary of the computational cases

每個算例都是從無量綱時間t+=0 (t+≡t/τν,其中 τν為黏性時間尺度) 時充分發展的水平槽道湍流開始模擬的,并在t+=2.84×104時終止.長時間的模擬保證了顆粒達到了最終統計上的穩定狀態[37].顆粒在t+=0 時被隨機地釋放到整個計算域中,每個顆粒的初始速度被設定為顆粒位置處的流體速度.對于所有的統計數據,用尖括號 〈〉 代表系綜平均,在實際統計過程中表示了在與壁面平行的水平面內的空間平均和多個時刻的時間平均.

2 結果與討論

本節通過顆粒平均濃度的壁法向廓線,以及與壁面平行的薄層內顆粒的瞬時分布、顆粒Vorono?分析和角分布函數,分別探討顆粒間碰撞對顆粒的湍泳和傾向性聚集現象的影響.

2.1 顆粒的分布

首先,為了評估顆粒間碰撞對顆粒湍泳現象的影響,圖3 給出了顆粒平均濃度的壁法向廓線.其中,顆粒濃度用槽道的體平均濃度n0無量綱化.如圖3 所示,當不考慮顆粒間碰撞時,大/小顆粒的濃度在壁面附近達到最大值,并隨著y+的增大而迅速地降低,表明顆粒有向壁面遷移的趨勢,即前文所述的湍泳現象.相比于小顆粒,大顆粒在壁面附近的濃度更高而在外區的濃度更低,意味著大顆粒的湍泳現象更強.當考慮顆粒間碰撞時,顆粒的濃度廓線變得十分平坦,僅隨著y+的增大而輕微地改變.這表明在流動的發展過程中,顆粒首先在湍泳作用下向壁面聚集,隨后近壁面處高頻率的顆粒間碰撞驅使顆粒向槽道中心遷移,最終導致顆粒濃度表現出平坦的壁法向廓線.因此,在槽道湍流中顆粒間碰撞顯著抑制了顆粒的湍泳現象.此外,與Johnson 等[38]的結論類似,隨著碰撞恢復系數e的降低,顆粒濃度在槽道內區 (外區) 有輕微的增加 (降低).但是,非完全彈性碰撞與完全彈性碰撞情形之間沒有顯著差異.因此下文僅對比完全彈性碰撞與無碰撞的情況.

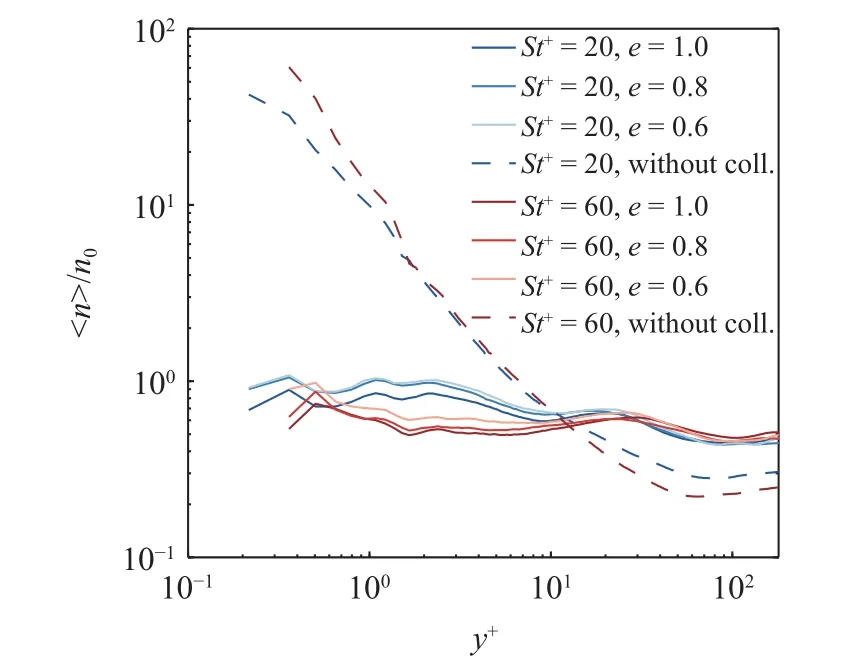
圖3 顆粒平均濃度的壁法向廓線: 藍色和紅色實線 (虛線) 分別對應考慮 (不考慮) 顆粒間碰撞時的小顆粒和大顆粒Fig.3 Wall-normal profiles of mean particle concentration: the blue and red solid lines (dashed lines) correspond to the small and large particles,respectively,with (without) considering inter-particle collisions

其次,為了探索顆粒間碰撞是否對顆粒的傾向性聚集產生顯著影響,我們展示了顆粒在不同水平面內的瞬時分布.圖4(a)～圖4(c)分別展示了t+=2.84×104時算例II 和III 在黏性底層、緩沖層和槽道中心的瞬時流場分布和顆粒位置分布.圖4(a)對應的速度脈動為y+=3.72 處,顆粒位置處于y+∈[2.64,4.82];圖4(b)對應的速度脈動為y+=18.10 處,顆粒位置處于y+∈[15.52,20.75];圖4(c)對應的速度脈動在y+=168.93 處,顆粒位置處于y+∈[161.57,176.31] .在圖4中,左側表示不考慮顆粒間碰撞的情形,右側表示考慮了顆粒間碰撞的情形;灰色點和黑色點分別代表了小顆粒和大顆粒.

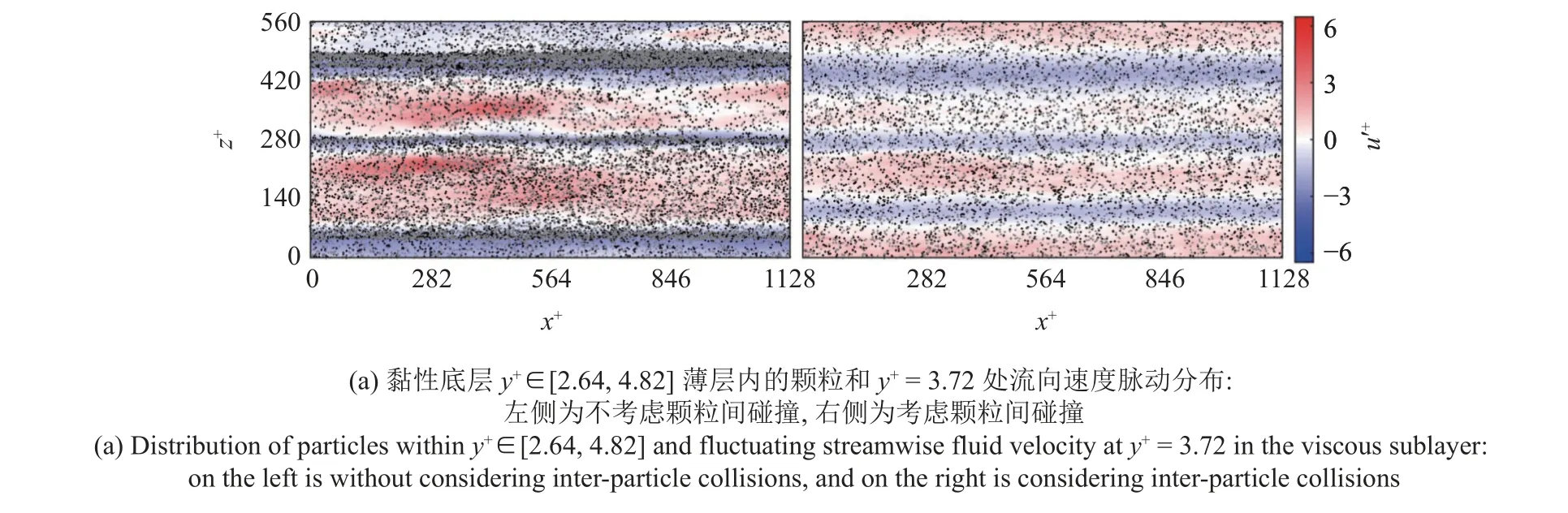
圖4 顆粒 (流體速度脈動) 在與壁面平行薄層 (平面) 內的瞬時分布Fig.4 Instantaneous distribution of particles (fluid fluctuating velocity) within a thin layer (plane) parallel to the wall

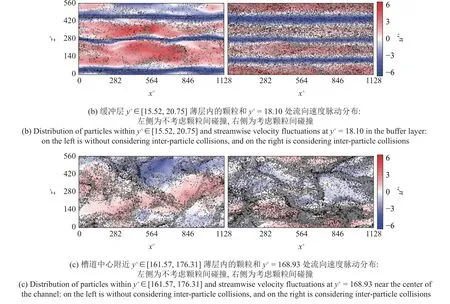
圖4 顆粒 (流體速度脈動) 在與壁面平行薄層 (平面) 內的瞬時分布 (續)Fig.4 Instantaneous distribution of particles (fluid fluctuating velocity) within a thin layer (plane) parallel to the wall (continued)

如圖4 所示,因為小顆粒和大顆粒的St數十分相近,兩者的聚集模式沒有顯著差別.另外,從圖4(a)和圖4(b)中可以看出,在近壁區,當不考慮顆粒間碰撞時,顆粒傾向于聚集在流場的低速區 (即u′+＜0),形成了流向長度達l+約等于或大于1000 的條帶狀結構.而當考慮顆粒間碰撞時,顆粒的分布變得非常均勻,表明顆粒間碰撞傾向于驅使顆粒更加均勻地分布,從而抑制顆粒在湍流場中的傾向性聚集.在圖4(c)中,與不考慮顆粒間碰撞相比,考慮顆粒間碰撞后槽道中心顆粒的聚集僅有非常輕微的增強,但兩種情況均表現為絲帶狀結構.這是因為在槽道中心處顆粒的濃度較小,顆粒間碰撞發生的頻率非常低.此外,值得注意的是,因為顆粒在近壁區的濃度和水平面內的分布被顯著改變,因此其對湍流的調制作用也非常不同.如圖4(a)和圖4(b)所示,當不考慮顆粒間碰撞時,流場低速條帶沿展向分布不均勻,展向間距約為220 δν(δν為黏性長度尺度).而當考慮顆粒間碰撞后,流場低速條帶沿展向分布變得較為均勻,且展向間距減小約為140 δν.

2.2 顆粒的聚集

接下來,為了定量刻畫顆粒間碰撞對顆粒聚集程度的影響,對不同壁法向處水平薄層內的顆粒進行二維Vorono?分析.在Vorono?分析中,水平面根據顆粒的位置被分解成有限數量的Vorono?單元,其中每個單元都包含了比其他任何顆粒更接近該顆粒的點的集合[39].作為示例,圖5 展示了不考慮顆粒間碰撞時y+∈[170,180] 薄層內根據顆粒位置劃分的Vorono? 視圖.從圖5 可以看出,Vorono?單元的面積與當地的顆粒濃度成反比,因此Vorono?單元面積的概率分布可以被視為一個恰當的衡量顆粒聚集程度的物理量.

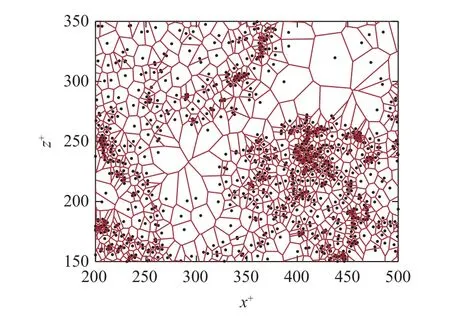
圖5 水平薄層 y+∈[170,180] 內顆粒Vorono? 分析的示例Fig.5 Example of Vorono? analysis of particles within a horizontal thin layer in the range y+∈[170,180]

此外,圖6(a)和圖6(b)分別呈現了小顆粒和大顆粒在黏性底層y+∈[2.64,4.82],緩沖層y+∈ [15.52,20.75],槽道中心附近y+∈[161.57,176.31] 3 個薄層內Vorono單元面積A的概率密度函數 (probability density function,PDF).其中,紅色和黑色曲線分別代表了不考慮和考慮顆粒間碰撞的情形,Vorono?單元面積A被其平均值 〈A〉 無量綱化.為了方便比較,圖中還用虛線顯示了均勻隨機分布顆粒的無量綱Vorono?面積的PDF,理論分析表明它服從 Γ 分布[40].

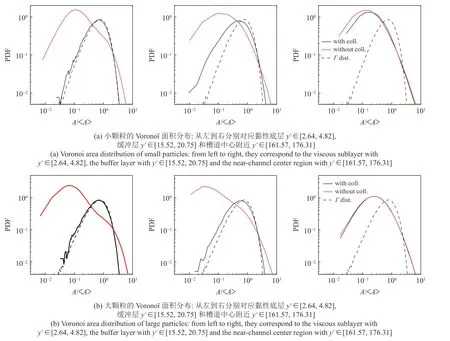
圖6 不同壁法向位置處顆粒的Vorono?面積分布Fig.6 Vorono? area distribution of particles at different wall-normal positions

對于考慮/不考慮顆粒間碰撞的算例和不同壁法向位置的薄層,Vorono?面積分布和隨機 Γ 分布之間均存在兩個交點.對于所有情況,因為Vorono面積小于左側第一個交點的概率密度大于隨機 Γ 分布(實線高于虛線),即小Vorono面積 (高濃度) 出現的概率高于均勻分布,因此對應的位置可以被認為是一個顆粒團.同理,因為Vorono面積大于右側第2 個交點的概率密度大于均勻隨機 Γ 分布 (實線高于虛線),即大Vorono?面積 (低濃度) 出現的概率高于均勻隨機分布,因此對應的位置可以被認為是一個空隙.

從圖6(a)可以看出,對于小顆粒而言,不考慮顆粒間碰撞時黏性底層和緩沖層內Vorono?面積的PDF 與均勻隨機 Γ 分布差異較大,左右兩側均顯著高于 Γ 分布,表明顆粒存在大范圍的高濃度和低濃度區域,即顆粒處于聚集狀態.當考慮顆粒碰撞時,黏性底層和緩沖層內Vorono?面積的PDF 與均勻隨機 Γ 分布之間的差異顯著減小.這意味著顆粒間碰撞的確降低了顆粒的非均勻分布程度.特別是在黏性底層內,Vorono?面積的PDF 幾乎完全服從 Γ 分布,表明考慮顆粒間碰撞時黏性底層的顆粒變成了均勻分布的狀態,這與瞬時圖4 一致.對于大顆粒而言,顆粒間碰撞對Vorono?面積分布的影響與小顆粒的情況相似,但是此時顆粒間碰撞的影響在緩沖層內更強.

值得注意的是,在槽道中心附近,考慮顆粒間碰撞后Vorono?面積的PDF 也表現出朝均勻分布輕微靠近的趨勢,表明顆粒分布變得更加均勻,這與圖4(c) 的顆粒瞬時分布結果不符.這是因為不同Vorono?單元面積差異巨大 (見圖5),無量綱化之后可能會損失兩端極值點的細節,造成Vorono?面積PDF 的不光滑波動 (見圖6).因此導致槽道中心處小樣本情況下不合理的結果.

為此,Liu 等[41]基于Vorono?劃分定義了局部顆粒空隙率 ε (local voidage),其能較好地解決該問題(見圖7).對于顆粒i,其空隙率可表示為

圖7 不同壁法向位置處顆粒的局部空隙率分布Fig.7 Local voidage distribution of particles at different wall-normal positions

其中,Ai表示顆粒i所處Vorono?單元的面積,為顆粒i的水平投影面積,因此Ai-表示顆粒i的局部流體面積.圖7(a)和圖7(b)分別呈現了小顆粒和大顆粒在黏性底層y+∈[2.64,4.82],緩沖層y+∈[15.52,20.75],槽道中心附近y+∈[161.57,176.31] 3 個薄層內顆粒局部空隙率的PDF.其中,紅色和黑色曲線分別代表了不考慮和考慮顆粒間碰撞的情形.從圖7(a)和圖7(b)中清楚地觀察到,顆粒局部空隙率主要分布在 ε ＞0.95 的區間,這是因為本文算例中顆粒的體積分數僅為～10-4量級.此外,與不考慮顆粒間碰撞相比,考慮顆粒間碰撞后局部空隙率PDF 曲線在黏性底層和緩沖層內變得更加平坦 (即小空隙率的概率增加而大空隙率的概率減小),表明顆粒分布更加均勻.相反,對于槽道中心,空隙率PDF 曲線變得更加陡峭,表明顆粒更加聚集,與圖4(c)的瞬時分布一致.

進一步,為了明確顆粒間碰撞對顆粒聚集形態的影響,采用二維角分布函數 (angular distribution function,ADF) 對其進行量化,ADF被定義為[42-43]

其中 δNi(r,θ) 是顆粒i位于中心的徑向 [r,r+δr] 和角度方向 [θ,θ+δθ] 范圍內包含的顆粒數,N是水平薄層區域內的顆粒總數,平均 〈〉 是對薄層內所有顆粒上實施的.這里,θ=0?和 θ=90?分別對應于展向和流向.對于流向和展向上靠近邊界的顆粒,使用了周期性的邊界條件.ADF表征了顆粒在水平面上統計平均的聚集結構,提供了顆粒聚集在距離和方向上各向異性的度量.

圖8(a)和圖8(b)分別展示了不考慮和考慮顆粒碰撞時小顆粒在黏性底層y+∈[2.64,4.82],緩沖層y+∈[15.52,20.75],槽道中心y+∈[161.57,176.31] 3 個薄層內的ADF結果.因為對稱性,圖中僅展示了第一象限的結果.從圖8(a)可以看出,當不考慮顆粒間碰撞時,在黏性底層和緩沖層內小顆粒的ADF表現為沿x軸的細長條狀,表明顆粒聚集的平均結構是各向異性的流向條帶狀結構,其長度超過了 1.5δ .在槽道中心,顆粒的ADF表現為近似的圓形,表明顆粒的平均結構是各向同性的.這也可以從圖4(c)的顆粒瞬時分布中觀察到,雖然顆粒為絲帶狀結構,但是其朝向為完全隨機的,在統計平均后表現為各向同性.如圖8(b)所示,當考慮顆粒間碰撞時,黏性底層的平均各向異性條帶狀結構完全消失,小顆粒的ADF不存在任何清晰的結構.緩沖區的各向異性條帶被顯著抑制,其流向長度僅為 0.5δ 左右.槽道中心的顆粒ADF變化并不顯著,僅輕微地向流向拉伸,與圖4(c)的顆粒瞬時分布一致.同樣,這是因為該區域顆粒的濃度較低,顆粒間碰撞發生的頻率非常小.類似的ADF結論也適用于大顆粒,如圖9 所示.唯一的區別是大顆粒ADF的條帶結構在緩沖層內也被完全破壞,表明此時大顆粒均勻地分布.需要強調的是,顆粒在低速條帶中的聚集,通常是顆粒受到近壁流向渦的作用在槽道展向產生定向運動造成的.當考慮顆粒間碰撞時,顆粒間碰撞會促進顆粒的展向混合,這種混合效應使得顆粒近壁處位置分布變得更加均勻 (見圖6～圖9),整體濃度分布也更加平坦 (見圖3).

圖8 小顆粒的ADFFig.8 ADF of small particles

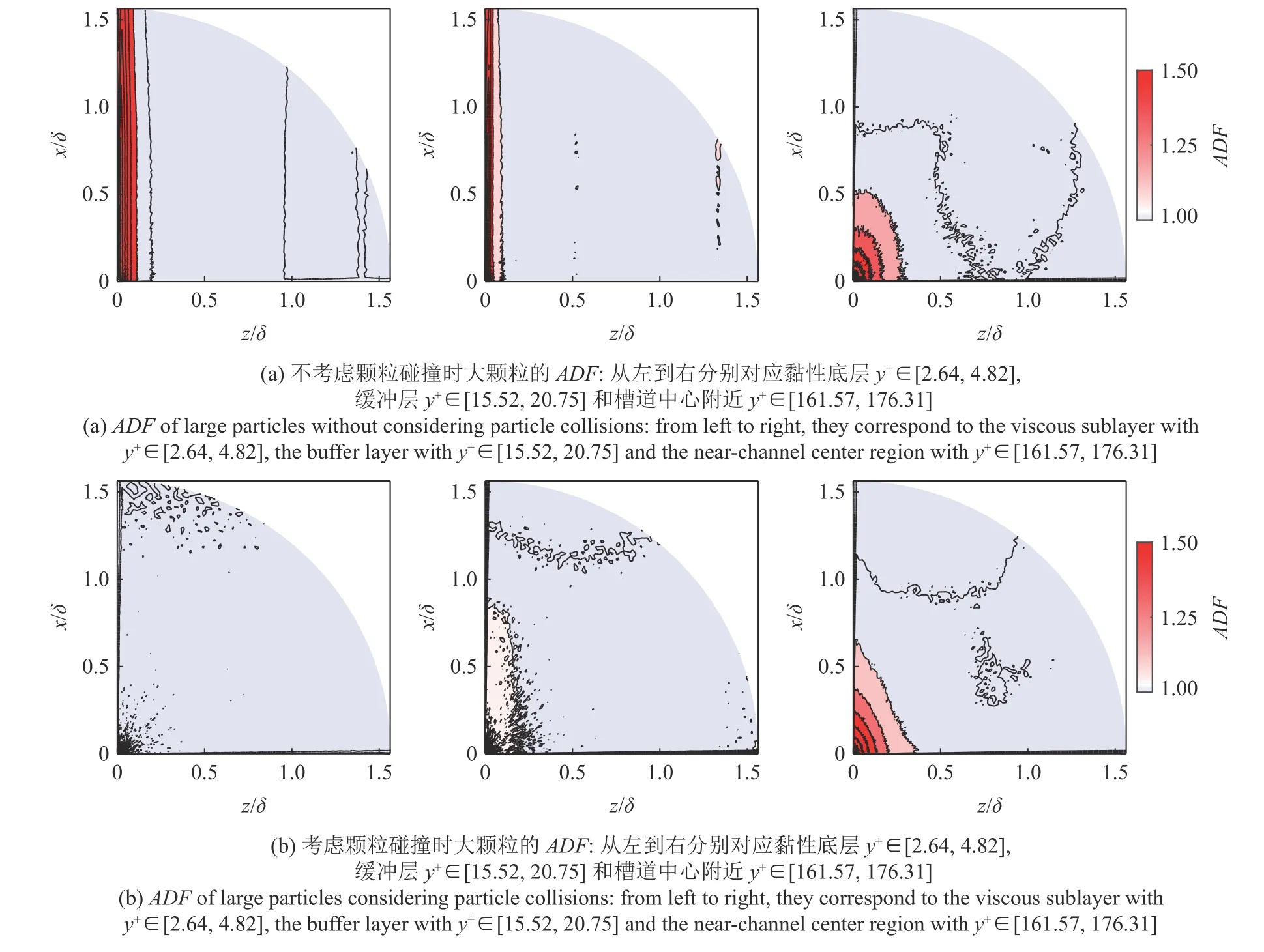
圖9 大顆粒的ADFFig.9 ADF of large particles

3 結論

本文基于歐拉-拉格朗日點顆粒框架,在顆粒的平均體積分數和質量分數分別為的條件下,采用直接數值模擬方法,考慮顆粒-湍流雙向耦合作用以及顆粒間的碰撞,通過不同壁法向位置處水平薄層內顆粒的Vorono?面積概率分布及其角分布函數分析,系統地研究了攜雙分散顆粒的水平槽道湍流中顆粒間碰撞對顆粒聚集程度和聚集模式的影響.本文得到主要結論如下.

(1) 當不考慮顆粒間碰撞時,顆粒有向壁面移動的趨勢,導致顆粒的濃度在壁面附近最大且隨高度的增加而迅速地降低,即湍泳現象.同時,在黏性底層和緩沖層中,顆粒傾向于聚集在流場的低速區,形成條帶狀顆粒團聚,即傾向性聚集現象.

(2) 當考慮顆粒間碰撞時,顆粒間碰撞引起顆粒向槽道中心遷移,顆粒濃度的壁法向廓線變得非常平坦,意味著顆粒間碰撞顯著抑制了顆粒的湍泳現象.

(3) 另一方面,顆粒間碰撞導致顆粒在黏性底層和緩沖層的條帶狀結構完全消失,這是因為傾向性聚集引起的局部高濃度顆粒條帶被顆粒間碰撞破壞,表明顆粒間碰撞同時也極大地抑制了顆粒的傾向性聚集現象.