解題教學:關注學生“五見”意識的培養和強化

楊利剛

(江蘇省蘇州中學 215007)

解題教學是數學教學中的一個重要組成部分,是教師最為熟悉、最為常用的教學形式之一．數學解題教學是解題活動的教學,解題活動是一種有意識的思維活動,既要有結果也要有過程．解題思路的探求和解答過程的呈現主要反映了思維活動的過程,解題答案主要反映了解題活動的結果．解題教學不僅要獲得解題活動的結果(答案),更要呈現解題活動的必要過程,即暴露數學解題的思維活動過程[1],并且讓學生積極主動地參與其中、感受其中．

本文中的“五見”是指:思考有主見、審題有預見、答題有遠見、卡題有另見、答畢有回見．通過具體的教學實踐,筆者以為,在數學解題教學活動中教師是學生思考的引領者、啟發者,是學生思維的評價者、調控者;學生是積極主動的思考參與者,是知識內容、數學方法的習得者．教學的本質不僅僅在于傳授更在于激勵、喚醒、鼓舞,關注學生解題思考中“五見”意識的培養,使學生在解題思考中自發、自覺地領悟,進一步提高數學解題的水平和能力,提升數學素養,促進個體的思維發展．

1 在數學解題思考中,樹立主見意識

“學之道,在于悟”,學好數學的關鍵在于對學習內容和方法的內化與領悟,而不是簡單模仿和機械做題．學生應該具有自己的想法、自己的主見(盡管是不太成熟的)．

數學學習強調學生的獨立思考和智力參與,形成自己的思考主見.學習的自主性尤為重要,可以說,真正深入、高質量的數學學習必然含有探究的成分[2]．立足于學生的日常學習,教學方法的設計中要特別關注學生的自主性、能動性和創造性,使學生擁有更多的主見和信心．

因此,解題教學中,教學素材要能夠自然地吸引全體學生,問題思考能讓所有的學生主動參與,學生的學習過程是獨立思考基礎上的合作交流和相互啟發,教學節奏是教師有備而來、張弛適度的科學調控從而漸入佳境．

下面結合一道涉及函數導數不等式恒成立以及求解參數最值的習題教學過程,談些體會,以期與讀者交流切磋．

(2)若關于x的不等式F(x)≤mx-1對任意的x>0恒成立,求整數m的最小值．

2 在數學審題中,喚起預見意識

題目條件提示我們解題應從何處下手、預示“可知”,并啟發解題手段．弄清條件就等于弄清行動的起點、明確解題行動的方向．題目的求解結論暗示著求解結果,便于我們在解題過程中進行調整和優化．

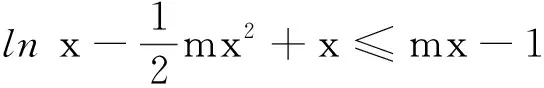
課堂教學中,教師首先引導學生讀題分析,明確題意,并且開始初步的獨立思考．接下來了解學生的解題想法,得到了如下的初步解題思路．

預見瞭望解答過程中避免了對參數m的分類討論,但回顧以往的解題經歷,此做法未必能得到預期結果,最終可能無功而返,比如函數h(x)在區間(0,+∞)上是單調函數(讓學生回想之前做過的相關問題,起到預警的作用)．

(1)若m≤0時,φ′(x)>0,則函數φ(x)是(0,+∞)上的單調增函數,且當x→+∞時,φ(x)→+∞,所以不滿足φ(x)max≤0.

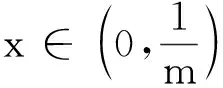
說明在數學審題中,打開學生的思路,引導學生自覺預見解題的方向,初步確定解題的基本程序、可能用到的數學方法,強化對問題處理的理性決策意識,進而逐步提升對問題解決的整體駕馭能力．

3 在問題作答中,提升遠見能力

課堂教學中停頓一定的時間,提醒學生思考,鼓勵學生去體會和感悟:

說明題目的結論告訴我們向何方前進、預告“需知”,并引導解題方向．弄清了結論就等于弄清了行動的目標,也隨身帶上了糾正偏差的指南針．解答過程中的遠見是在審題預見的基礎上、在解題推進中的積極思維監控,針對出現的結果而采取的應對策略,避免了走彎路和錯路,提高了解題的正確率和解題效率．

4 在解答受困時,誘發另見靈感

解題思考時會受到以往經驗的遷移和影響,但面對變化了的問題,可能需要另辟蹊徑,靈活應對,采取新辦法才能突破困局,使問題獲解．

圖1

如果待證不等式lnx≤x2+x-1變形為 lnx-x2≤x-1的話,則由函數圖象可以直觀地感受(圖2)．

5 在解題完成后,養成回見習慣

歷經上述問題的思考作答過程后,教師應趁熱打鐵,引導學生作解題回顧,體會、鞏固解題成果,培養學生自覺的解題回見習慣．具體地說:回見解題方法,領會數學思想;梳理解題過程,體悟解題策略;重溫難點突破,培養意志品質．

(1)回顧解題的通性通法,如題解中的參變分離、整體構造函數的帶參討論(預見2的思路方法),使學生扎實掌握相應的解題方法．

(2)對比解題方法和策略,體會面對具體受阻問題時的靈活應變．如先控制參數m的取值范圍,而后猜想、確定相應的值,再進行充分性的證明,豐富解題經驗,拓展解題視野,優化思維品質．

(3)感悟數學學習應該具備堅韌不拔的頑強意志,敢于發表自己的主見,發揚勇于探索的科學精神,進一步激發、強化對數學學習的興趣和熱情．

解題教學實踐表明:分析典型例題的解題過程是學生學會解題的有效途徑,解題教學中的例子應盡可能是范例,具有典型性、教育性,少而精,學生才能記得住,才容易領悟．解題教學是師生再發現與再創造的過程,不僅要把“題”作為研究的對象,把“解”作為研究的目標,而且要把“解題活動”作為對象,把學會“數學地思維”、促進“人的思維發展”作為目標．