高動態(tài)條件下的自行高炮穩(wěn)定跟蹤力矩分析

江騰耀,李 偉,曹瑩星,王偉偉,耿曉虎

(西北機(jī)電工程研究所, 陜西 咸陽 712000)

0 引言

自行高炮作為將火力與機(jī)動合二為一的防空武器,是野戰(zhàn)陸軍伴隨防空的重要裝備,隨著戰(zhàn)場形勢的快速變化,自行高炮具備行進(jìn)間射擊能力已成為其適應(yīng)作戰(zhàn)條件的迫切需求。穩(wěn)定跟蹤系統(tǒng)是自行高炮實現(xiàn)行進(jìn)間射擊的關(guān)鍵部件,通過方位軸和俯仰軸伺服電機(jī)驅(qū)動高炮指向射擊諸元跟蹤目標(biāo)并隔離車體姿態(tài)擾動。目前的自行高炮在行進(jìn)間射擊時必須有合理的車速及較好的路況條件[1],當(dāng)車體處于高速機(jī)動和復(fù)雜路面的高動態(tài)條件下,火炮所受的擾動力矩的幅值和頻率都會有明顯的增加[2-4],尤其是高射角情況下,雙軸電機(jī)的輸出力矩會產(chǎn)生巨大變化,影響穩(wěn)定跟蹤系統(tǒng)效能的有效發(fā)揮。由于高炮射角高,且為了降低火線高,目前自行高炮的俯仰部分大部分采用質(zhì)量偏心配置,利用平衡機(jī)抵消質(zhì)量偏心產(chǎn)生的靜態(tài)重力偏心力矩,同時減小伺服系統(tǒng)的功率,但各俯仰角下抵消后的殘余力矩仍會給系統(tǒng)帶來擾動[5-6]。此外,質(zhì)量偏心會導(dǎo)致在載體運動狀態(tài)下產(chǎn)生額外的動載荷干擾力矩,對穩(wěn)定跟蹤精度產(chǎn)生嚴(yán)重的影響。

目前,國內(nèi)外火炮指向穩(wěn)定方面已取得了一些研究成果。文獻(xiàn)[7]初步建立了直驅(qū)式自行高炮射擊線穩(wěn)定系統(tǒng)的動力學(xué)模型,分析了不同俯仰角下干擾力矩的影響。文獻(xiàn)[8]定量分析了搖擺角及目標(biāo)運動對船載轉(zhuǎn)塔隨動系統(tǒng)隨動力矩的影響,對搖擺角的幅值、周期和相位造成的影響進(jìn)行了詳細(xì)的分析。文獻(xiàn)[9]提出了基于大地坐標(biāo)系下速率陀螺閉環(huán)的火炮自穩(wěn)定控制方法,有效地克服了較高頻帶的車體姿態(tài)干擾。但上述文獻(xiàn)側(cè)重于分析載體姿態(tài)對干擾力矩的影響,并未將載體的平動速度考慮到力矩的分析中,文獻(xiàn)[13-14]中的建模包含了由車體由平動產(chǎn)生的干擾力矩,但尚未對該力矩產(chǎn)生的影響作系統(tǒng)性的分析。

目前,未查到存在質(zhì)量偏心且處于平動與搖擺條件下的自行高炮穩(wěn)定跟蹤系統(tǒng)動力學(xué)建模與力矩分析,為此有必要建立完整的高動態(tài)自行高炮穩(wěn)定跟蹤系統(tǒng)動力學(xué)模型,對擾動力矩的主要成分進(jìn)行分析,并建立其與伺服電機(jī)等效輸出力矩(下文簡稱“輸出力矩”)的聯(lián)系,為支持行進(jìn)間射擊的自行高炮炮控系統(tǒng)設(shè)計提供理論依據(jù)。在載體旋轉(zhuǎn)運動過程中,干擾力矩可分為對轉(zhuǎn)軸動不平衡旋轉(zhuǎn)慣性力矩和由于原點不在重心而導(dǎo)致的偏心力矩[15],一般情況下對軸轉(zhuǎn)動不平衡旋轉(zhuǎn)慣性力矩的影響極小,偏心力矩主要包括由重力產(chǎn)生的靜態(tài)偏心力矩和由運動產(chǎn)生的動載荷干擾力矩。本文中根據(jù)自行高炮穩(wěn)定跟蹤系統(tǒng)的結(jié)構(gòu)特點,建立了雙軸歐拉動力學(xué)方程并對該系統(tǒng)進(jìn)行了數(shù)值仿真,系統(tǒng)分析了影響動載荷干擾力矩大小的因素,定量分析了動載荷干擾力矩與輸出力矩之間的關(guān)系。

1 坐標(biāo)系定義

自行高炮穩(wěn)定跟蹤控制系統(tǒng)涉及多個坐標(biāo)系,通過坐標(biāo)系間的變換來描述車體、炮塔與自行高炮身管之間的相對運動關(guān)系。

本文中所取坐標(biāo)系包含了慣性坐標(biāo)系Onxnynzn(簡稱n系)、車體坐標(biāo)系Obxbybzb(簡稱b系)、炮塔坐標(biāo)系Ohxhyhzh(簡稱h系)、身管坐標(biāo)系Opxpypzp(簡稱p系),各個坐標(biāo)系均符合右手定則,其建立方法參考文獻(xiàn)[13],自行高炮指向結(jié)構(gòu)及各坐標(biāo)系的關(guān)系如圖1所示。

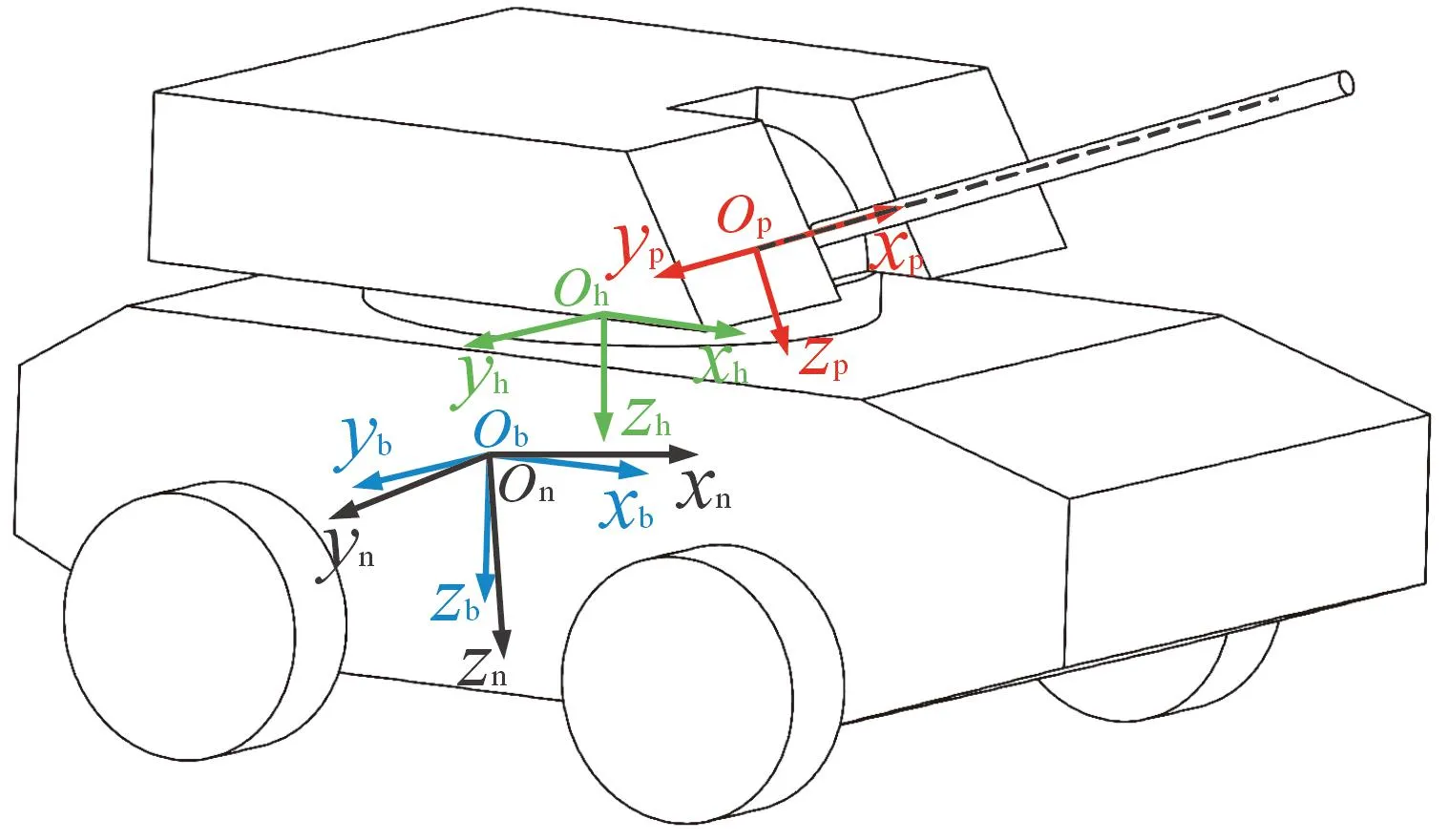
圖1 自行高炮指向結(jié)構(gòu)及其坐標(biāo)示意圖

車體坐標(biāo)系和慣性坐標(biāo)系之間的轉(zhuǎn)換關(guān)系可用3個歐拉角來描述,φ、θ、ψ分別為車體橫滾角、俯仰角、航向角。以慣性坐標(biāo)系為基準(zhǔn),為了分析簡單且接近實際,采用ψ→θ→φ的順序分別繞對應(yīng)軸進(jìn)行3次旋轉(zhuǎn)可得到車體坐標(biāo)系Obxbybzb,其對應(yīng)的變換矩陣為

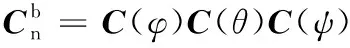
(1)

式(1)中:

βb為炮塔相對于車體的方位向姿態(tài)角,則車體坐標(biāo)系轉(zhuǎn)換為炮塔坐標(biāo)系的變換矩陣為

(2)

則由慣性坐標(biāo)系到炮塔坐標(biāo)系的變換矩陣為

(3)

εb為自行高炮身管相對于炮塔的俯仰姿態(tài)角,等同于自行高炮身管相對于車體的俯仰姿態(tài)角,炮塔坐標(biāo)系轉(zhuǎn)換為身管坐標(biāo)系的變換矩陣為

(4)

則由慣性坐標(biāo)系到身管坐標(biāo)系的變換矩陣為

(5)

2 穩(wěn)定跟蹤系統(tǒng)雙軸動力學(xué)模型

2.1 運動學(xué)模型

(6)

(7)

(8)

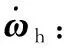
(9)

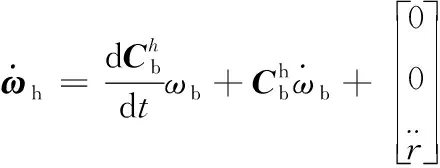
(10)

(11)

(12)

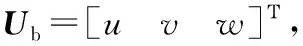
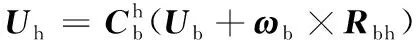
(13)

(14)

(15)

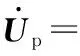
(16)

2.2 動力學(xué)模型

根據(jù)剛體旋轉(zhuǎn)運動的歐拉動力學(xué)方程[15]:

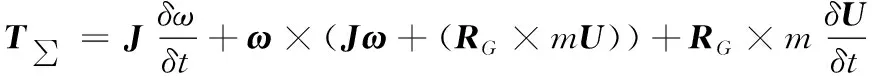
(17)

式(17)中:T∑為合外力矩;J為剛體對運動坐標(biāo)系原點的慣性張量;m為剛體的質(zhì)量;ω為運動坐標(biāo)系下剛體轉(zhuǎn)動角速度,δω/δt為角速度在運動坐標(biāo)系下的相對變化率;RG為運動坐標(biāo)系原點指向質(zhì)心的向量;U為運動坐標(biāo)系下原點的速度,δU/δt為原點平動速度在運動坐標(biāo)系下的相對變化率。

方位軸合力矩ThΣ和俯仰軸合力矩TpΣ可表示為

(18)

聯(lián)立式(16)和式(17)可得到方位軸電機(jī)等效輸出力矩Th和俯仰軸電機(jī)等效輸出力矩Tp的表達(dá)式

(19)

(20)

重力偏心力矩、平衡機(jī)力矩、補(bǔ)償力矩殘差與εb的關(guān)系如圖2、圖3所示。

圖2 不同俯仰角下的重力偏心力矩與平衡機(jī)力矩

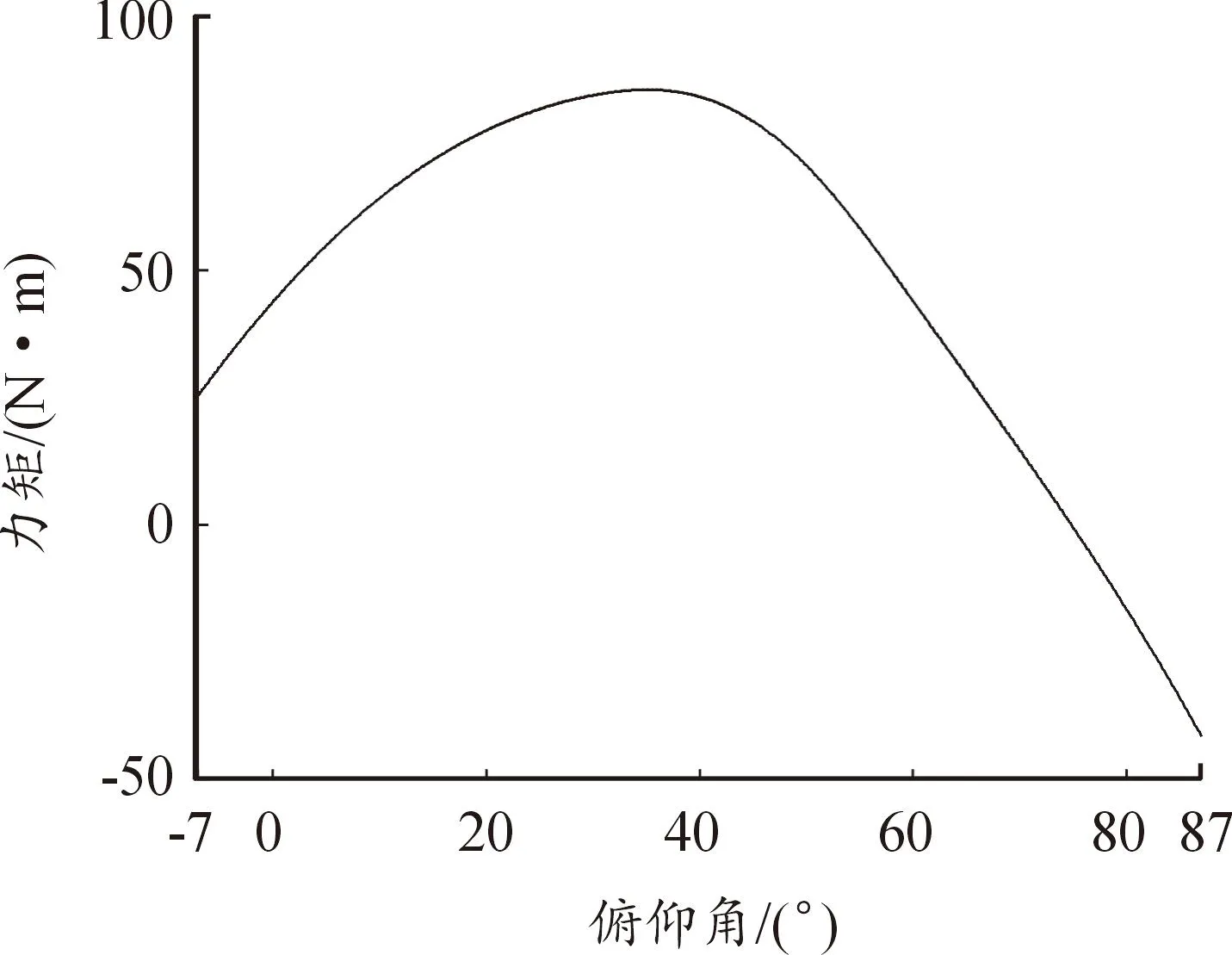
圖3 不同俯仰角下的力矩殘差

令方位軸總偏心力矩為Thr,俯仰軸總偏心力矩為Tpr

(21)

則雙軸電機(jī)等效輸出力矩可簡化表示為

(22)

3 仿真分析

3.1 仿真條件

自行高炮穩(wěn)定指向動力學(xué)模型主要輸入包括車體姿態(tài)信息、n系目標(biāo)指向信息、b系原點平動信息,根據(jù)建立的動力學(xué)模型進(jìn)行仿真,分別分析車體搖擺但無平動、車體平動但無搖擺、車體同時做平動和搖擺這3種情況下的自行高炮執(zhí)行穩(wěn)定跟蹤所具有的動載荷偏心力矩和輸出力矩,仿真流程如圖4所示。由于自行高炮穩(wěn)定跟蹤系統(tǒng)的物理結(jié)構(gòu)特性,只需考慮方位軸力矩在zh軸的有效分量和俯仰軸力矩在yp軸的有效分量。

圖4 自行高炮穩(wěn)定跟蹤系統(tǒng)動力學(xué)仿真流程圖

不考慮靜摩擦轉(zhuǎn)矩,自行高炮穩(wěn)定指向系統(tǒng)的主要機(jī)械結(jié)構(gòu)參數(shù)為:mh=4 000 kg,mp=1 100 kg;xbh=0 m,ybh=0 m,zbh=-1 m;xhG=0.25 m,yhG=0 m,zhG=-0.1 m;xhp=0.3 m,yhp=0 m,zhp=-0.2 m;xpG=0.4 m,ypG=0 m,zpG=0 m;bhz=-90 N·m/rad,bpy=-40 N·m/rad;方位炮塔與自行高炮身管在各自旋轉(zhuǎn)中心下的慣性張量為

文獻(xiàn)[6]已詳細(xì)討論了車體姿態(tài)角變化幅值、車體姿態(tài)角變化頻率,以及不同相位條件下分別對自行高炮高低軸和方位軸輸出力矩的影響,得到了載體姿態(tài)角變化幅值越大,頻率越大,雙軸輸出力矩也越大的結(jié)論。如無特殊說明,本文引入的車體姿態(tài)角干擾均滿足以下條件:車體姿態(tài)角φ、θ、ψ的變化周期為2 s,變化幅值為7°,無相位差(即φ=θ=ψ=7sin(πt))。

3.2 車體搖擺但無平動時的力矩分析

3.2.1穩(wěn)定時俯仰指向角對雙軸力矩的影響

假設(shè)車體坐標(biāo)系原點的平動速度恒為零,給定慣性坐標(biāo)系下的方位指向角為0°(βn=0°),俯仰指向角分別為15°(即εn=15°,下同)、30°、45°、60°時,所得的方位和俯仰軸力矩分別見圖5、圖6,其中Thr為方位軸動載荷干擾力矩,Th為方位軸電機(jī)等效輸出力矩,Tpr為俯仰軸動載荷干擾力矩,Tp為俯仰軸電機(jī)等效輸出力矩。由圖5、圖6可知,當(dāng)俯仰指向角分別為15°、30°、45°、60°時,方位軸動載荷峰值分別為1 515、1 550、1 596、1 663 N·m,約為對應(yīng)輸出力矩峰值的45%、75%、120%、33%;俯仰軸動載荷峰值分別為290、481、646、778 N·m,約為對應(yīng)輸出力矩峰值的82%、86%、89%、92%。

圖5 不同俯仰指向角下的方位軸力矩

圖6 不同俯仰指向角下的俯仰軸力矩

隨著俯仰指向角的增加,方位軸和俯仰軸的動載荷峰值均有所增加,方位軸動載荷受俯仰指向角影響較小,在車體僅做搖擺運動時對輸出力矩的影響有限,隨著俯仰指向角的增大,炮塔坐標(biāo)系的角速度及角加速度會急劇變大,使得方位軸的旋轉(zhuǎn)運動慣性力矩成為輸出力矩的主導(dǎo)項之一,總偏心力矩與旋轉(zhuǎn)運動慣性力矩抵消,改變了輸出力矩峰值的大小以及出現(xiàn)的時間。俯仰軸的平衡機(jī)抵消了大部分由重力產(chǎn)生的靜態(tài)偏心力矩,且穩(wěn)定指向時旋轉(zhuǎn)運動慣性力矩接近0,輸出力矩主要由動載荷主導(dǎo),故動載荷和輸出力矩大致呈現(xiàn)同樣的變化趨勢,兩者的峰值較為接近。

3.2.2動態(tài)跟蹤時雙軸力矩的變化

當(dāng)方位指向角變化幅值為60°,俯仰指向角變化幅值為30°,周期為2π s,所得的方位和俯仰軸力矩分別見圖7、圖8。由圖7、圖8可知,當(dāng)方位角和俯仰角指向均隨時間變化時,方位軸動載荷峰值約為輸出力矩峰值的25%,俯仰軸的動載荷峰值約為輸出力矩峰值的62%。

圖7 動態(tài)跟蹤時的方位軸力矩

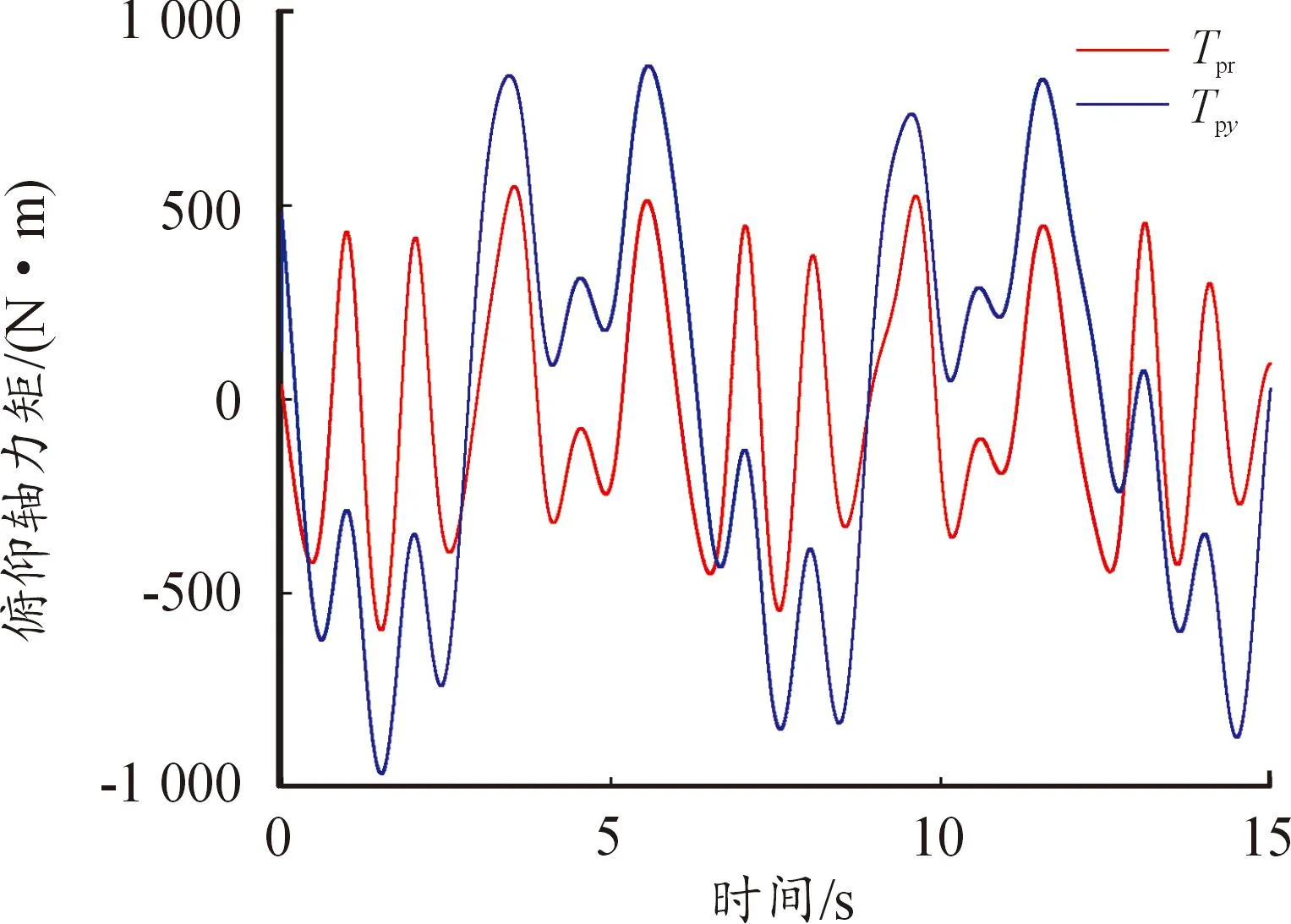
圖8 動態(tài)跟蹤時的俯仰軸力矩

動態(tài)跟蹤指向時,俯仰軸的動載荷、靜態(tài)偏心力矩以及旋轉(zhuǎn)運動慣性力矩共同影響了輸出力矩,動載荷峰值與靜態(tài)指向時基本相同;俯仰軸的平動慣性力矩增加明顯,動載荷峰值相較于靜態(tài)指向時有一定增大。俯仰軸和方位軸的旋轉(zhuǎn)角速度及角加速度相對于靜態(tài)指向時變化幅值更大,導(dǎo)致雙軸旋轉(zhuǎn)運動慣性力矩大幅增加,疊加上雙軸各自的動載荷和靜態(tài)偏心力矩后,方位軸和俯仰軸的輸出力矩都有了明顯的增加。

3.3 車體平動但無搖擺時的力矩分析

3.3.1無姿態(tài)擾動時車體平動對雙軸力矩的影響

車體在無姿態(tài)擾動條件下做水平運動,在車體無側(cè)滑的情況下(車體坐標(biāo)系原點平動速度在yb、zb軸的分量為0),給定俯仰指向角為45°,方位指向角分別為15°,車體的初始平動速度為10 m/s,疊加周期為2 s,幅值分別為0、2、4、6 m/s2的余弦加速度信號,得到圖9、圖10所示的雙軸力矩曲線。由圖9可知,當(dāng)方位角指向為15°時,加速度幅值每增加2 m/s2,方位軸輸出力矩峰值增加約679 N·m,動載荷峰值增加約518 N·m,動載荷峰值約為輸出力矩峰值的76%;加速度幅值每增加2 m/s2,俯仰軸的動載荷與輸出力矩峰值增加約622 N·m,動載荷峰值約為輸出力矩峰值的95%。

圖9 車體僅做平動時的方位軸力矩

圖10 車體僅做平動時的俯仰軸力矩

當(dāng)車體僅做勻速運動時,俯仰軸的總偏心力矩和輸出力矩皆為身管重力偏心力矩被平衡機(jī)補(bǔ)償后的殘差,恒為-75 N·m。引入車體加速度干擾后,聯(lián)立式(15)、式(19)可知,俯仰軸力矩中的有效項僅為動載荷和重力偏心力矩殘差,且動載荷和加速度大小呈正比。當(dāng)方位指向角為0°時,上述情況下俯仰軸對方位軸的反作用力矩-Tp在zh軸的有效分量恒為0,故方位軸的動載荷和輸出力矩恒為0。當(dāng)方位指向角為15°時,此時炮塔偏心坐標(biāo)和加速度方向不位于同一直線,同時受到來自俯仰軸的反作用力,故方位軸的動載荷峰值和輸出力矩峰值均與加速度幅值呈正比。

3.3.2動態(tài)跟蹤時雙軸力矩的變化

車體在無姿態(tài)擾動條件下做水平運動,在車體無側(cè)滑的情況下,車體的初始平動速度為10 m/s,疊加周期為2 s,幅值為2π m/s2的余弦加速度信號,當(dāng)方位指向角變化幅值為60°,俯仰指向角變化幅值為30°,周期為2π s時,所得的方位和俯仰軸力矩分別見圖11、圖12。由圖11、圖12可知,當(dāng)方位角和俯仰角指向均隨時間變化時,方位軸動載荷峰值約為輸出力矩峰值的72%,俯仰軸動載荷峰值約為輸出力矩峰值的95%。相比車體只做搖擺的情況,方位軸的動載荷峰值和輸出力矩峰值分別增加了約1.6倍、7.1倍,俯仰軸的動載荷峰值和輸出力矩峰值分別增加了約3.3倍、6.4倍

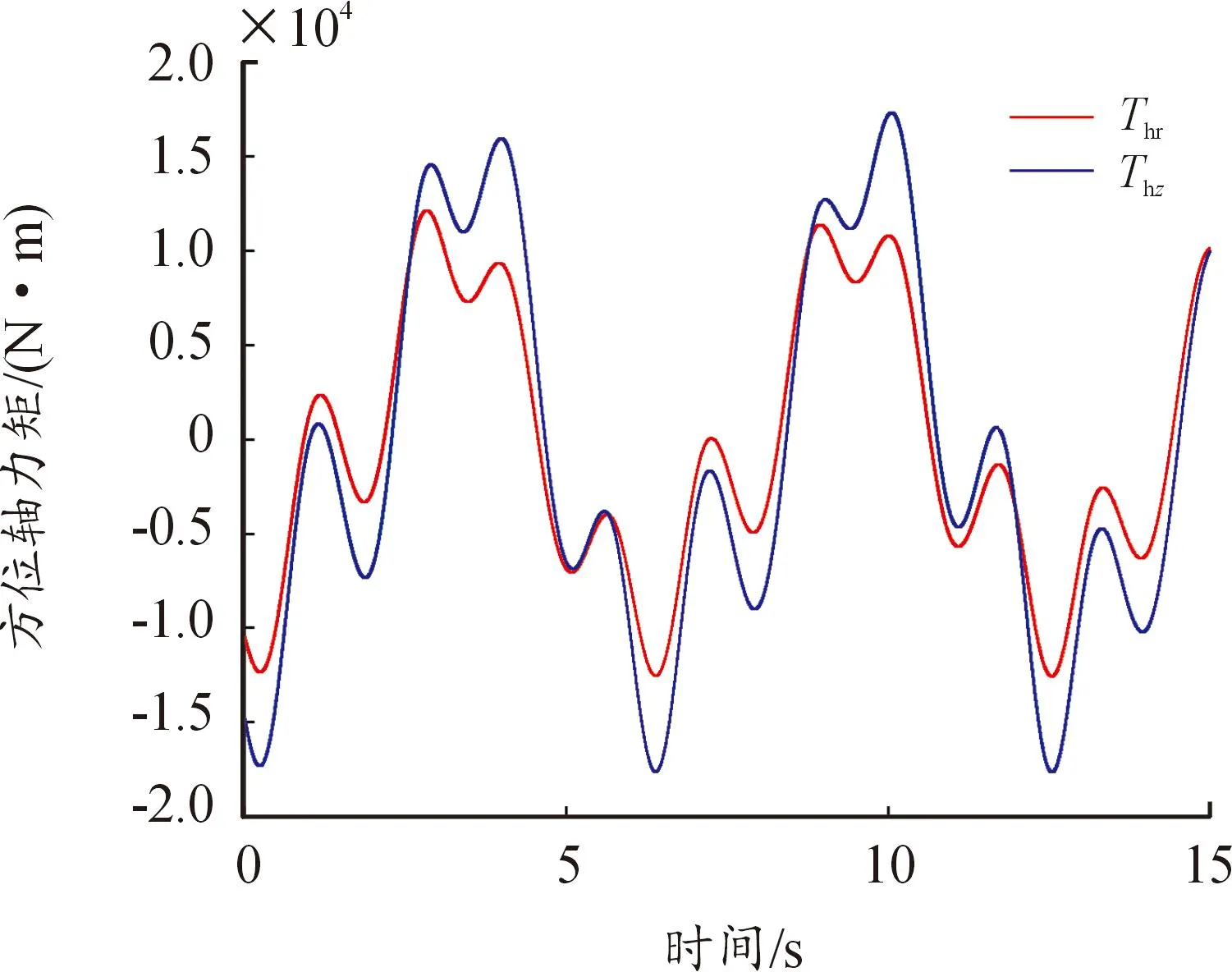
圖11 動態(tài)跟蹤時的方位軸力矩

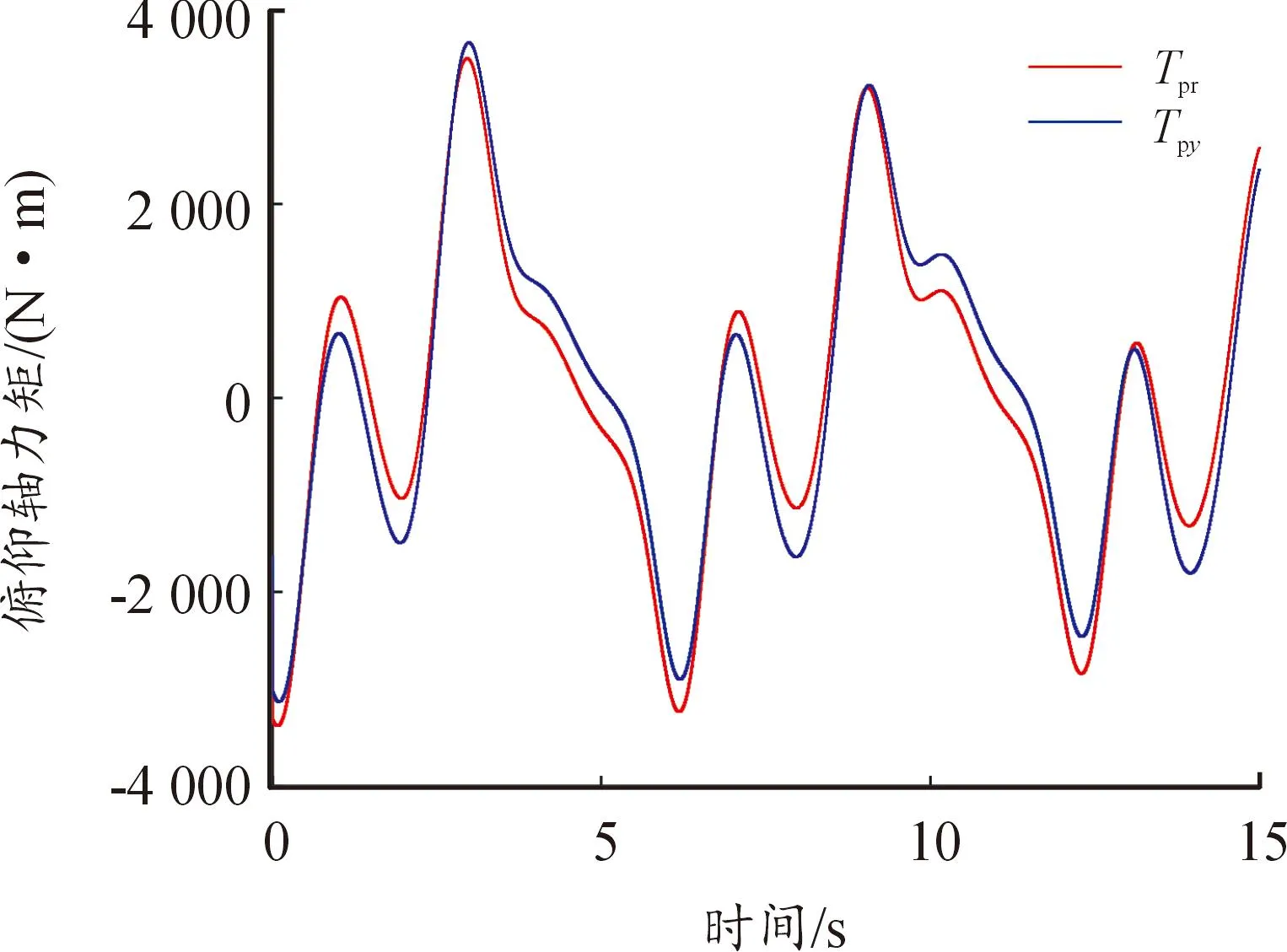
圖12 動態(tài)跟蹤時的俯仰軸力矩

在車體僅做平動運動時進(jìn)行動態(tài)跟蹤指向,方位軸由重力產(chǎn)生的靜態(tài)偏心力矩恒為0,僅有旋轉(zhuǎn)運動慣性力矩和動載荷影響輸出力矩,該情況下俯仰軸的動載荷增幅明顯,主導(dǎo)了輸出力矩的變化,俯仰軸動載荷對輸出力矩的影響更大,峰值與其輸出力矩更為接近。

3.4 車體復(fù)合運動時的力矩分析

3.4.1存在姿態(tài)擾動時車體平動對雙軸力矩的影響

車體存在姿態(tài)角擾動,無側(cè)滑且無下墜,給定俯仰指向角為45°,方位指向角為0°,車體的平動速度分別為5、10、15 m/s時,所得的力矩見圖13、圖14。可知,方位軸動載荷峰值分別約為輸出力矩峰值的68%、71%、74%,俯仰軸動載荷峰值分別約為輸出力矩峰值的91%、94%、96%。平動速度每提高5 m/s,方位軸動載荷峰值和輸出力矩峰值分別增加約2 350、3 100 N·m,俯仰軸動載荷峰值和輸出力矩峰值增加約580 N·m。

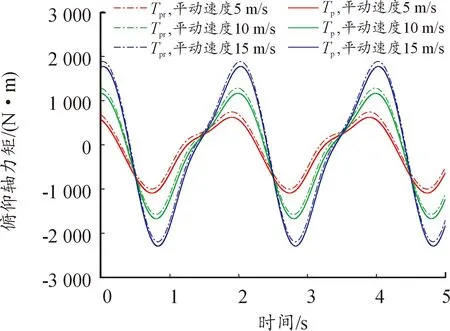
圖14 不同車體平動速度下的俯仰軸力矩

由運動產(chǎn)生的動載荷大小直接受車體平動速度大小的影響,平動速度越大,雙軸的動載荷和輸出力矩的峰值越大,并且由于在穩(wěn)定條件下俯仰軸的旋轉(zhuǎn)運動慣性力矩極小,平動狀態(tài)下俯仰軸的輸出力矩完全由動載荷所主導(dǎo)。

3.4.2車體加速度幅值對雙軸力矩的影響

車體存在姿態(tài)角擾動,無側(cè)滑且無下墜,給定俯仰指向角為45°,方位指向角為0°,車體的初始平動速度為10 m/s,給以周期為2 s,幅值分別為2、4、6 m/s2的余弦加速度信號,得到如圖15、圖16所示的雙軸力矩曲線。可知,方位軸的動載荷峰值分別約為對應(yīng)輸出力矩峰值的68%、70%、71%,俯仰軸的動載荷峰值分別約為對應(yīng)輸出力矩峰值的93%、92%、91%。

相對于車體無加速度的情況,僅雙軸力矩各自的動載荷發(fā)生了變化,由于動載荷同時受雙軸角速度與車體坐標(biāo)系原點速度的影響,在不同相位的車體平動加速度干擾下,方位軸的動載荷和輸出力矩的峰值會有較大差別,文中采取的僅為其中的一種情況,相位的影響較為復(fù)雜,此處不做深入探討。

圖15 不同車體加速度幅值下的方位軸力矩

圖16 不同車體加速度幅值下的俯仰軸力矩

3.4.3行進(jìn)間跟蹤動態(tài)目標(biāo)時雙軸力矩的變化

車體存在姿態(tài)角擾動,無側(cè)滑且無下墜,車體的初始平動速度為10 m/s,給以周期為2 s,幅值為2π m/s2的余弦加速度信號,當(dāng)方位指向角變化幅值為60°,俯仰指向角變化幅值為30°,周期均為2π s時,所得的方位和俯仰軸力矩分別見圖17、圖18。可知,在自行高炮行進(jìn)間跟蹤動態(tài)目標(biāo)時,方位軸動載荷峰值約為輸出力矩峰值的76%,俯仰軸的動載荷峰值約為輸出力矩峰值的92%;相比車體只做搖擺的情況,方位軸的動載荷峰值和輸出力矩峰值分別增加了約2.5倍、6.9倍,俯仰軸的動載荷峰值和輸出力矩峰值分別增加了約3.2倍、6.3倍。

在行進(jìn)間跟蹤且車體存在姿態(tài)干擾的情況下,雙軸的動載荷主導(dǎo)了各自輸出力矩的變化,且相對于車體無平動時的情況,雙軸的動載荷和輸出力矩均有極為明顯的增幅。

圖17 行進(jìn)間保持動態(tài)跟蹤時的方位軸力矩

圖18 行進(jìn)間保持動態(tài)跟蹤時的俯仰軸力矩

4 結(jié)論

對自行高炮穩(wěn)定跟蹤系統(tǒng)雙軸力矩進(jìn)行了系統(tǒng)分析,建立了雙軸穩(wěn)定跟蹤系統(tǒng)歐拉動力學(xué)方程,結(jié)合典型系統(tǒng)結(jié)構(gòu)參數(shù)進(jìn)行了動力學(xué)仿真,分析了帶有平衡機(jī)情況下的自行高炮車體姿態(tài)角與平動速度對雙軸的動載荷和輸出力矩的影響,得到了以下結(jié)論:

1) 車體僅做搖擺運動且指向角穩(wěn)定時,俯仰指向角的大小對雙軸力矩有直接影響,雙軸的動載荷隨著俯仰角增大而變大,俯仰軸的輸出力矩由其動載荷主導(dǎo),方位軸的動載荷對方位軸輸出力矩的影響較為有限;

2) 車體僅做平動運動且指向角穩(wěn)定時,雙軸的動載荷均與車體加速度的大小呈正比,俯仰軸的輸出力矩與其動載荷近似,方位軸的輸出力矩僅受俯仰軸的反作用力以及自身動載荷的影響;

3) 車體平動且搖擺時,雙軸的動載荷和輸出力矩都隨平動速度增大而明顯增大,雙軸的動載荷主導(dǎo)了各自輸出力矩的變化;

4) 無論是否存在車體姿態(tài)擾動,自行高炮行進(jìn)間跟蹤相比無平動條件下跟蹤,其雙軸的總偏心力矩和輸出力矩都有極大幅度的增加,且行進(jìn)過程中動載荷對輸出力矩的影響更為明顯。

5) 質(zhì)量偏心與運動耦合產(chǎn)生的動載荷干擾力矩會給自行高炮行進(jìn)間穩(wěn)定跟蹤帶來極大的負(fù)面影響,影響穩(wěn)定跟蹤系統(tǒng)的精度,在設(shè)計時應(yīng)當(dāng)盡量減少質(zhì)量偏心。

6) 雙軸力矩的量化分析對電機(jī)的匹配選型有重要的參考價值,可考慮引入力矩補(bǔ)償來提高穩(wěn)定跟蹤閉環(huán)系統(tǒng)的性能,這對設(shè)計和優(yōu)化自行高炮穩(wěn)定跟蹤系統(tǒng)控制器具有重要的研究意義。