基于預(yù)測校正法的迫擊炮外彈道模型解算方法

羅超元,王雙川,許 錦

(陸軍步兵學(xué)院, 南昌 330103)

0 引言

隨著模擬訓(xùn)練的逐步推開,炮兵模擬訓(xùn)練系統(tǒng)的運用也更加廣泛。在系統(tǒng)研發(fā)過程中,要根據(jù)裝定諸元在虛擬場景中模擬出較為準確的彈道軌跡,從而確定彈著點的位置,以滿足用戶對仿真精度的要求。

為準確復(fù)現(xiàn)出迫擊炮彈丸的運行軌跡,需要對外彈道進行準確的模型構(gòu)建和解算。目前關(guān)于提升外彈道仿真精度的研究主要思路是對外彈道模型進行細化。主要有3類模型:質(zhì)點外彈道模型、剛體外彈道模型、準剛體外彈道模型。質(zhì)點外彈道模型參數(shù)少、解算速度快,但由于模型簡單,精度難以有較大的提升。因此,相關(guān)研究開始綜合考慮同時對內(nèi)、外彈道仿真進行優(yōu)化從而提升仿真精度[1]。剛體外彈道模型、準剛體外彈道模型通過將更多的影響因素納入到模型中對模型進行細化,以提升仿真精度。但與此同時模型參數(shù)也隨之增加,尤其是剛體外彈道模型較為復(fù)雜,解算需要更多的時間[2-3]。因此,以解算方法為切入點提升外彈道仿真的精度具有一定的必要性。

在現(xiàn)有的普通迫擊炮外彈道仿真研究中,解算方法以常規(guī)的微分方程數(shù)值解法為主[4]。吳晉等[5]采用歐拉法對外彈道模型解算,對虛擬場景中的外彈道可視化建模與仿真,但由于歐拉法是二階方法,精度較低。張進強等[6]將歐拉法、改進的歐拉法、龍格庫塔法(R-K)運用到外彈道可視化仿真中,從多種方法中進行擇優(yōu),結(jié)果表明,龍格庫塔法最為精確。董理贏等[7]運用變步長的4階龍格庫塔法對122 mm榴彈炮外彈道進行了解算,得到了更為準確的結(jié)果。近年來解算方法研究的開始轉(zhuǎn)向數(shù)值穩(wěn)定性較高的迭代修正方法[8]。從現(xiàn)有的研究來看,龍格庫塔法是最常用的方法,目前已經(jīng)有較多的相關(guān)研究[9-14],精度難以有進一步的提升。此外,關(guān)于其他方法的研究較少,實際應(yīng)用過程中缺少可供選擇的替代方法。

基于上述研究需求和研究現(xiàn)狀,本文中擬采用預(yù)測校正法探究提升外彈道模型解算精度的有效途徑,在現(xiàn)有的彈丸質(zhì)心運動模型基礎(chǔ)之上,對模型進行進一步調(diào)整,并結(jié)合阿達姆斯(Adams)線性多步法中的巴什福思法(Adams-Bashforth)與莫爾頓法(Adams-Moulton)設(shè)計一種預(yù)測校正的解算方法,并與同階精度的龍格庫塔法與線性多步法的解算結(jié)果進行對比分析,以驗證預(yù)測校正方法的有效性。

1 數(shù)學(xué)模型

1.1 問題描述

在迫擊炮模擬訓(xùn)練中,裝定諸元后系統(tǒng)需要根據(jù)初始表尺來對彈道軌跡進行仿真,從而確定虛擬場景中彈著點位置,射擊指揮再根據(jù)彈著點位置進行口令修正。準確找出彈丸落點,才能保證修正口令的正確性。因此,構(gòu)建準確的彈道模型,需要復(fù)現(xiàn)出準確的彈道軌跡。

1.2 基本假設(shè)

虛擬場景中重構(gòu)了迫擊炮的射擊條件,包括地形條件、彈道條件、氣象條件、地球條件,彈丸在飛行中主要受上述條件的影響。為建立更為細化的外彈道模型,這里在文獻[12]的基礎(chǔ)上,對迫擊炮外彈道的模型基本假設(shè)和參數(shù)進行調(diào)整,具體假設(shè)如下:

1) 假定炮口和彈著點在同一個水平面上,即炮目高低角為0;

2) 假定彈丸為軸對稱體,不考慮剛體運動,運動過程中攻角始終為0,將彈丸運動看作質(zhì)點運動;

3) 假定任意高度上風(fēng)速均為零,氣溫、氣壓為標準值,彈丸會受空氣阻力影響;

4) 假定裝藥溫度+15 ℃,空氣密度1.206 kg/m3,音速340 m/s,氣壓846.3 Pa,地面虛溫288.9 K;

5) 假定科氏重力加速度為零,地表面為平面,地球表面標準重力加速度9.8 m/s2,重力加速度會受射高影響;

在上述假設(shè)基礎(chǔ)上,彈丸在空氣中的飛行相當(dāng)于在二維空間中只受到空氣阻力和重力的質(zhì)點運動。

1.3 外彈道方程

在基本假設(shè)下,以炮口為原點建立二維直角坐標系,將橫縱速度進行分解,則經(jīng)典的外彈道微分方程組可轉(zhuǎn)換為式(1)的形式:

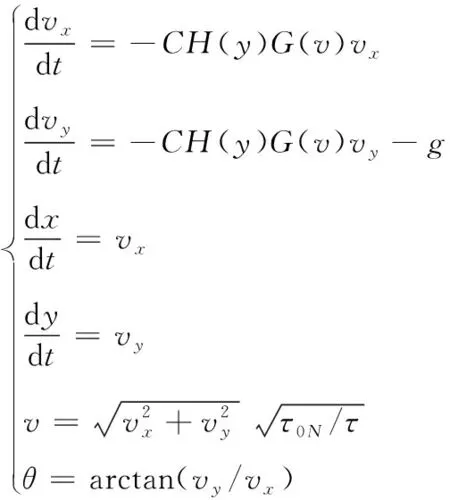
(1)

式(1)中:H(y)為空氣密度函數(shù),G(v)為空氣阻力函數(shù)。因為常規(guī)迫擊炮射擊距離不遠,彈道和射速也不高,所以空氣密度函數(shù)和阻力函數(shù)采用文獻[12]中的經(jīng)驗公式,在一定程度上可以保證模型的精度,如式(2)、式(3)所示:

H(y)=(1-2.190 4×10-5y)4.399

(2)

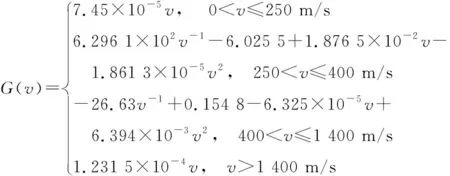
(3)

重力加速度g隨射高變化的函數(shù)如式(4)所示,其中g(shù)為實時重力加速度,地面標準重力加速度g0=9.8 m/s2,R為地球半徑,y為射高:

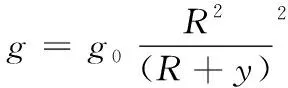
(4)

虛溫與射高的關(guān)系如式(5)所示,其中地面虛溫τ0=288.9 K。

τ=τ0-6.328×10-3y,y<9 300 m

(5)

2 解算方法設(shè)計

目前,關(guān)于外彈道仿真的研究是使用龍格庫塔法進行彈道微分方程的解算,解算方法的階數(shù)越大,仿真的精度越高,同時計算量也隨之增加。為兼顧解算效率,研究主要采用4階的龍格庫塔法,但精度依然有待提升。因此,可以將Adams線性多步法中的Adams-Bashforth方法和Adams-Moulton方法相結(jié)合,采用預(yù)測校正的方法來降低解算的誤差,提升彈道解算精度。

2.1 線性多步法

與龍格庫塔法不同的是,線性多步法在解算微分方程時期望利用前面已經(jīng)求得更多函數(shù)值來計算當(dāng)前得函數(shù)值,如果利用前k步的函數(shù)值,則線性多步法的一般形式,如式(6)所示:

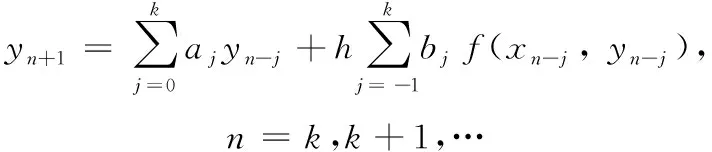
(6)

為使得解算結(jié)果具備可比性,采用理論上與4階龍格庫塔法同精度的線性多步法公式:Adams-Bashforth采用4步4階公式,Adams-Moulton采用3步4階公式,依托數(shù)值積分法可以得出Adams線性多步法公式。其中,4步4階Adams-Bashforth方法是顯式方法,如式(7)所示,截斷誤差為251h5y(5)(ξn)/729。3步4階Adams-Moulton方法為隱式方法,如式(8)所示,截斷誤差為-19h5y(5)(ξn)/720。

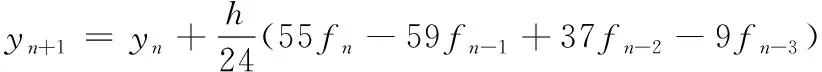
(7)

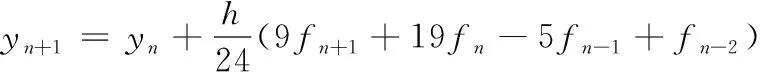
(8)

2.2 預(yù)測校正設(shè)計

對于一般的線性多步法,相同階數(shù)的隱式方法比顯示方法的數(shù)值穩(wěn)定性更好,結(jié)果更為精確[15-16]。但僅利用隱式方法很難求出某一點yn+1的函數(shù)值,因此先利用Adams-Bashforth顯示公式求解(預(yù)測)每一步的函數(shù)值,再利用Adams-Moulton隱式方法進行校正,結(jié)合2種方法的優(yōu)勢來提升解算精度。此外,如果每次預(yù)測矯正的迭代次數(shù)過多會造成額外的時間開銷,所以本文中對迭代次數(shù)進行了限制。具體的迭代過程如下:

1) 初始化條件:vx,vy,θ,x,y;

2) 用4階R-K方法計算vx,vy前4步的函數(shù)值;

3) isStop=False;

4) while not isStop do;

5) 用Adams-Bashforth公式預(yù)測vx,vy;

6)vx,vy代入Adams-Moulton公式進行校正;

7) 更新vx,vy;

8) 更新θ,x,y,τ,g,Hy,Gv;

9) 判斷是否滿足停止條件(y<0),滿足則令isStop=True。

其中,由于4階線性多步法顯示公式在初始時要利用前4步的值,因此,先用4級4階龍格庫塔方法分別求出彈丸運動過程中前4步2個方向的速度值,4級4階龍格庫塔法方法如式(9)所示。在迭代時,僅對2個方向的速度值進行一次預(yù)測和校正,在這個過程中,先利用Adams-Bashforth法計算初始預(yù)測值,如式(10)所示;再利用Adams-Moulton法進行迭代校正,將初值預(yù)測值代入式(11)右側(cè),得到一個校正函數(shù)值。其他變量的值根據(jù)2個方向上速度的變化進行更新。

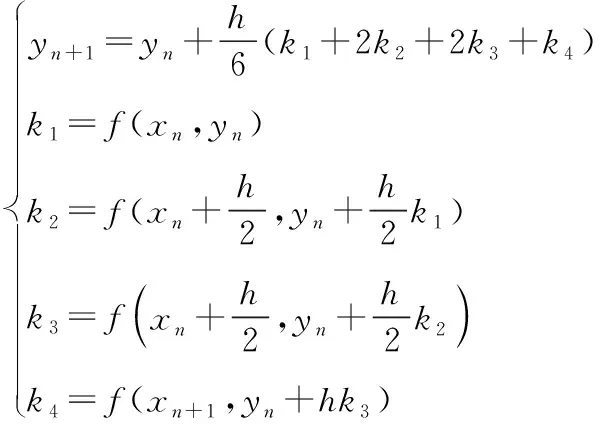
(9)

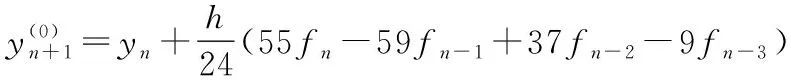
(10)

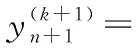
(11)

3 模型解算與分析

為檢驗第2節(jié)中設(shè)計的預(yù)測校正方法的有效性,分別用4階經(jīng)典龍格庫塔法(R-K)、Adams-Bashforth線性多步法(A-B)和預(yù)測校正法(PE)進行解算彈道模型,對解算結(jié)果的精度進行對比分析。彈道解算軟件環(huán)境采用Matlab 2010b,根據(jù)第2節(jié)的解算方法設(shè)計自行編寫解算程序,運行程序的計算機核心處理器為AMD Ryzen5 3500U,內(nèi)存12 G。

仿真初始條件設(shè)置如下:以82迫擊炮遠程殺傷榴彈4號裝藥為例,取表尺為1 000和716時的初始條件代入模型,經(jīng)換算初始傾角為45°和62.04°,設(shè)時間步長s為0.01 s,則初始條件為

t0=0 m/s,x0=0 m,y0=0 m,v0=238 m/s,θ0=45°/62.04°,g0=9.8 m/s,τ0=288.9 K,s=0.01 s。

代入初始條件進行模型解算,結(jié)果如下表所示,其中表1為射表真值、表2為仿真值、表3為仿真誤差百分比。

從表1—表3的解算結(jié)果中可以看出,2種初始傾角情況下,同階精度的龍格庫塔法和Adams-Bashforth線性多步法在射距、射擊最大高程、飛行時間、落角上的解算結(jié)果比較接近,Adams-Bashforth方法比龍格庫塔方法的解算精度低,但差距并不明顯。在3種解算方法中,預(yù)測校正的方法解算出的結(jié)果在精確度上具有明顯的優(yōu)勢。

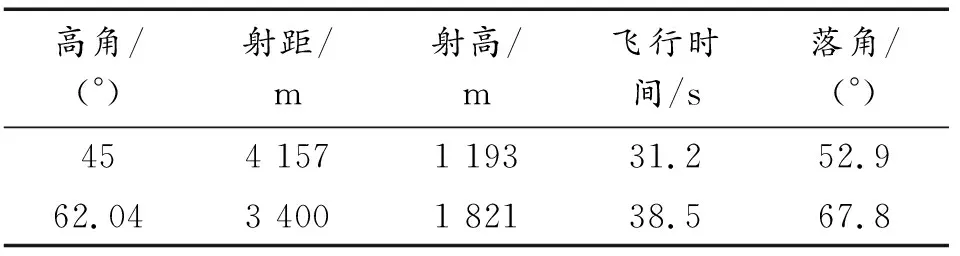
表1 射表真值

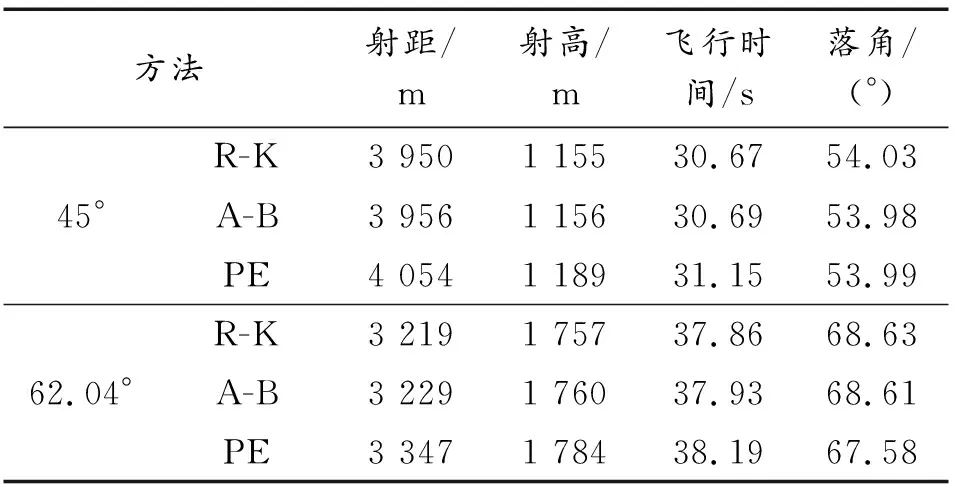
表2 仿真值

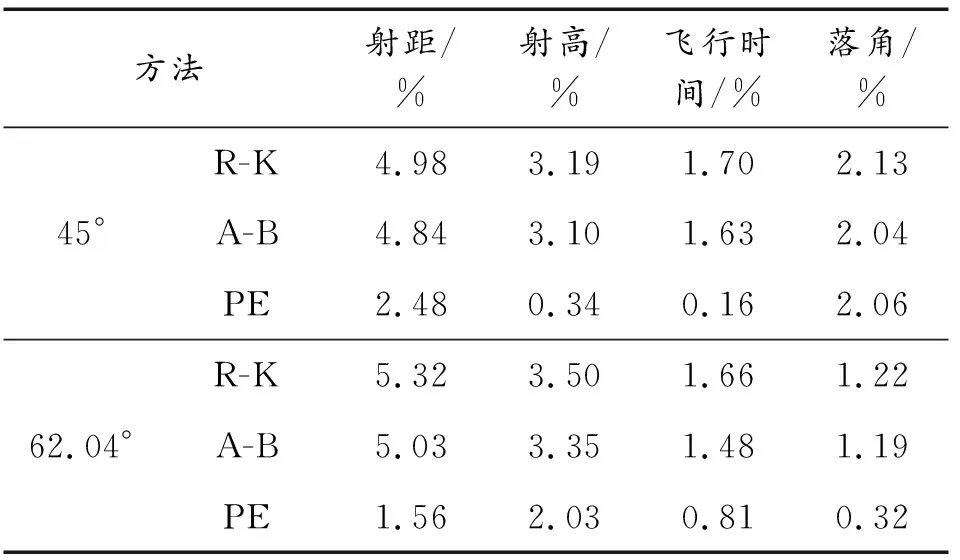
表3 仿真誤差百分比

初始傾角為45°時,解算時間如表4所示,表中為10次解算的平均時間和標準差。從時間代價來看,Adams-Bashforth線性多步法耗時最短,預(yù)測校正法解算時間較長,但相差不超過1倍,對預(yù)測校正方法的實用性的影響較小。

表4 解算時間

圖1—圖3分別為45°出射角時,外彈道的軌跡曲線、時間-速度曲線、時間-傾角曲線。從圖1中的外彈道軌跡可以看出,隨著彈丸飛行距離的增加,3種不同方法解算出的彈道軌跡逐漸分離,預(yù)測校正法解算的彈道軌跡飛行高度最高、飛行最遠,也最接近射表。圖2時間-速度曲線和圖3的時間-傾角曲線可以解釋這一現(xiàn)象,隨著時間的增加,預(yù)測校正方法解算出的彈丸速度始終比其他2種方法的解算結(jié)果大,彈丸傾角減少較慢,故此飛行高度和距離較遠。

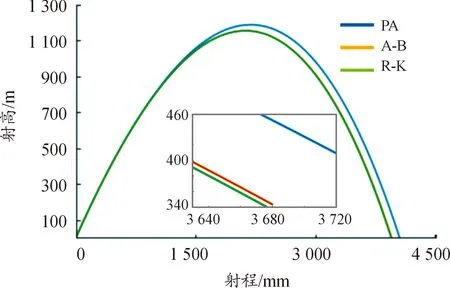
圖1 外彈道軌跡

圖2 時間-速度曲線

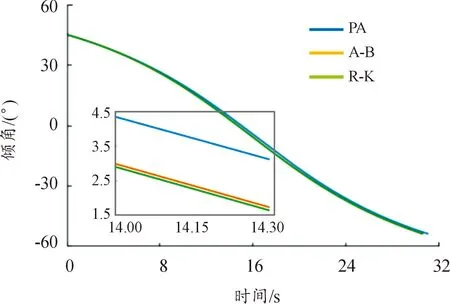
圖3 時間-傾角曲線

經(jīng)分析,主要有以下2點原因:一是研究的重點在于解算方法精度的提升,因此在構(gòu)建模型時,為簡化模型,采用了較為簡單的質(zhì)點運動模型,忽略了剛體運動等因素的影響,模型本身存在一定的誤差;二是微分方程的數(shù)值計算方法本身存在截斷誤差,隨著計算次數(shù)的增加累計誤差會逐漸增大,從彈道曲線、時間-速度、時間-傾角曲線的走勢來看龍格庫塔法和線性多步法解算精度小于預(yù)測校正法。

4 結(jié)論

為提升迫擊炮外彈道模型解算精度,設(shè)計了一種基于預(yù)測校正的解算方法,并構(gòu)建了外彈道模型對方法的有效性進行了驗證,結(jié)果表明:

1) 基于Adams-Bashforth和Adams-Moulton的預(yù)測校正方法在質(zhì)心外彈道模型解算精度上有一定的提升。

2) 設(shè)計的預(yù)測校正方法與傳統(tǒng)的龍格庫塔法和線性多步法相比具有明顯的優(yōu)勢,具備較高的實用性。

3) 研究成果為模擬訓(xùn)練系統(tǒng)中虛擬火炮的外彈道仿真提供了一種參考的解算方法,并啟發(fā)了后續(xù)的研究思路,后續(xù)的研究可以轉(zhuǎn)向?qū)⒎椒ㄟ\用到參數(shù)更多的剛體外彈道模型上,進一步提升仿真精確度。