飛行器軌跡的半參數估計方法

李振興,李 冬,劉 學

(中國人民解放軍91550部隊, 遼寧 大連 116023)

0 引言

飛行器試驗鑒定一般采用光學、雷達等多臺套精密測量設備對飛行器跟蹤測量,然后對所有設備的測量數據作融合處理,獲得飛行器軌跡的高精度估計,用于分離飛行器的制導工具誤差,進而評定飛行器的命中精度[1-3]。隨著飛行器制導元器件精密度的不斷提高,為保證制導工具誤差的有效分離,對軌跡估計的精度要求越來越高。設備測量誤差導致軌跡的估計值偏離真實值,是影響軌跡估計精度的關鍵因素,研究能夠最大限度抑制測量誤差的軌跡估計方法對于提高飛行器軌跡的估計精度有著重要意義。

飛行器軌跡估計的精度主要受2種測量誤差影響,第1種誤差是由設備內部熱噪聲、環境擾動等引起的隨機誤差,在零值附近隨機波動,一般根據統計規律融合多個測量數據對其作補償抑制。第2種誤差是系統誤差,是由設備標校不準確、時間不同步、大氣折射修正殘差等引起的測量偏差。飛行器軌跡估計通常根據系統誤差的變化規律進行參數化建模,例如建立常值模型、線性模型、周期模型等,采用參數估計方法同時估計軌跡和分離系統誤差,從而降低系統誤差對軌跡估計精度的影響[4-6]。然而,在實際測量中,受多種復雜誤差源的綜合影響,系統誤差往往不具有規律性,無法用參數模型對其進行建模描述,而如果不考慮這種不可參數建模的系統誤差,勢必會降低軌跡估計的精度。

針對無法利用參數估計方法分離不可參數建模系統誤差的問題,統計學界提出了半參數估計方法[7-9],用參數模型表示待估計的真實信號,用非參數表示不可參數建模的系統誤差,建立既含有參數又含有非參數的半參數回歸模型,采用半參數估計方法同時獲得參數分量和非參數分量的估計,可實現真實信號與系統誤差的有效分離,從而提高真實信號的估計精度。許多學者將半參數估計方法應用于人造衛星的軌道確定[10-12]。文獻[10]建立基于補償最小二乘的半參數聯合定軌模型,同時估計衛星軌道參數和模型誤差。文獻[11]針對天基測量確定初軌問題,提出了基于半參數模型的廣義正則化最小二乘估計方法,既有效抑制了不可參數建模系統誤差,又提高了初軌確定的穩定性。文獻[12]理論上證明了半參數回歸補償最小二乘估計法優于經典最小二乘法。文獻[13]將半參數估計方法應用于慣導離心機試驗中的加速度計誤差模型辨識,可同時辨識加速度計誤差模型參數和系統誤差。目前將半參數估計方法應用于飛行器軌跡估計問題的研究較少,文獻[14]利用多項式調制函數表示系統誤差,由軌跡估計后的殘差來估計多項式調制函數的系數,該方法本質上仍然是參數估計方法,多項式調制函數很難對實際應用中的復雜系統誤差進行精確表示,因此該方法對軌跡估計精度的提升效果有限。

文中針對飛行器軌跡估計的不可參數建模測量系統誤差的抑制問題,提出一種半參數估計方法。該方法建立既包含參數待估量又包含非參數待估量的半參數回歸模型,參數待估量為飛行器軌跡的樣條表示系數,非參數待估量為測量系統誤差,采用參數估計和非參數估計交替迭代的方式求解半參數回歸模型,參數估計利用非線性最小二乘法估計軌跡的樣條表示系數,非參數估計利用小波分析方法從殘差數據中分離系統誤差。最后從理論上分析了半參數估計方法的精度,并通過仿真實驗對文中方法的估計精度進行了驗證。

1 飛行器軌跡的參數估計

1.1 軌跡建模

(1)

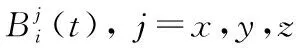
根據式(1),飛行器軌跡的樣條表示模型為

x(t)=B(t)α

(2)

1.2 測量模型

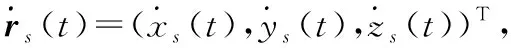
(3)

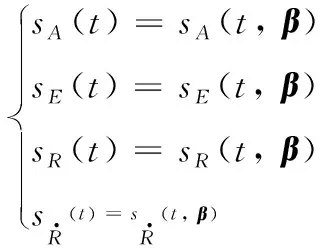
(4)

式(4)中:β=(β1,β2,…,βp)T為p維系統誤差參數向量。

發射坐標系向地心坐標系的旋轉矩陣記為C,地心坐標系向測站坐標系的旋轉矩陣記為G,測站和發射原點在地心坐標系下的矢量分別記為rs0=(xs0,ys0,zs0)T和rf0=(xf0,yf0,zf0)T,則飛行器的位置和速度從發射坐標系到測站坐標系的轉換關系表示為[1]

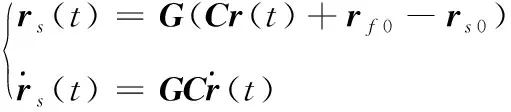
(5)

令y(t)為t時刻的所有測量參數組成的向量;根據式(3)和式(5),y(t)可表示為軌跡x(t)的函數:

y(t)=f(x(t))+s(t)+ε(t)

(6)

式(6)中:s(t)為測量的系統誤差向量,ε(t)為測量的隨機誤差向量,其協方差矩陣記為Σ(t)。將軌跡的參數模型(2)、系統誤差的參數模型(4)代入測量模型(6),可得到如下以樣條系數α和系統誤差參數β為未知參數的測量模型:

y(t)=z(t,α,β)+ε(t)

其中,z(t,α,β)=f(B(t)α)+s(t,β)。

1.3 參數估計

飛行器軌跡測量的采樣時刻記為t1,t2,…,tn,軌跡估計是根據所有采樣時刻測量數據y(t1),y(t2),…,y(tn)的融合值給出軌跡X=(x(t1),x(t2),…,x(tn))T的最優估計,從而獲得飛行器高精度的位置和速度。考慮到不同測站測量精度不一致,需利用測量隨機誤差的協方差矩陣對測量模型作歸一化處理[6],以實現不同測站多源數據的最佳融合:

Y=(Σ-1/2(t1)y(t1),…,Σ-1/2(tn)y(tn))T

Z(α,β)=(Σ-1/2(t1)z(t1,α,β),…,Σ-1/2(tn)z(tn,α,β))T

E=(Σ-1/2(t1)ε(t1),…,Σ-1/2(tn)ε(tn))T

其中,E服從均值為零協方差矩陣為單位矩陣的高斯分布,這樣便可建立以樣條系數和系統誤差參數為待估參數的非線性回歸模型:

Y=Z(α,β)+E

采用非線性最小二乘法估計樣條系數和系統誤差參數:

可采用高斯牛頓迭代法[1]求解上述非線性最小二乘問題。飛行器軌跡的估計為

其中,B=(B(t1),B(t2),…,B(tn))T。

2 飛行器軌跡的半參數估計

2.1 半參數估計

受測量設備狀態、環境因素的影響,測量系統誤差往往呈現復雜特性。例如圖1所示的某型光學設備俯仰角測量的系統誤差,對于這種復雜的系統誤差無法建立常值模型、線性模型、周期模型等參數模型,因此不能采用參數估計方法同時估計軌跡的樣條表示系數和分離系統誤差。以下將不可參數建模的系統誤差用非參數表示,建立既包含軌跡表示參數又包括非參數的半參數回歸模型,采用半參數估計方法求解半參數回歸模型,同時獲得軌跡和系統誤差的估計結果。

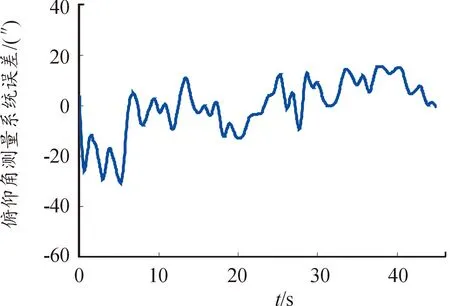
圖1 光學設備俯仰角測量的系統誤差

考慮不可參數建模系統誤差的影響,建立如下測量模型:

y(t)=f(B(t)α)+s(t)+ε(t)

利用采樣時刻t1,t2,…,tn的測量數據建立歸一化的半參數回歸模型:

Y=F(Bα)+S+E

(7)

其中

F(Bα)=(Σ-1/2(t1)f(B(t1)α),…,Σ-1/2(tn)f(B(tn)α))T

S=(Σ-1/2(t1)s(t1),…,Σ-1/2(tn)s(tn))T

模型(7)的待估量除了包括參數α,還包括非參數S,半參數估計方法需同時獲得參數α和非參數S的估計。

測量隨機誤差和系統誤差會在軌跡估計后的殘差數據中有所體現。其中,系統誤差通常表現為變化平緩的低頻信號,而隨機誤差為變化劇烈的高頻信號,可根據2種誤差的不同頻率特性采用小波分析方法[16]將兩者進行分離,從而提取殘差中的低頻信號,將其作為系統誤差的近似值,再將扣除系統誤差后的測量數據用于軌跡估計,可進一步改善軌跡估計的精度。

半參數估計采用軌跡估計和系統誤差分離交替迭代的方式實現,軌跡估計采用非線性最小二乘法,軌跡估計完成后,采用小波分析方法對殘差數據作系統誤差分離,利用分離結果對測量數據作修正,由修正后的測量數據再進行軌跡估計,進一步修正軌跡估計結果,這一過程反復迭代,直到殘差數據中不含系統誤差為止。半參數估計方法的原理如圖2所示。

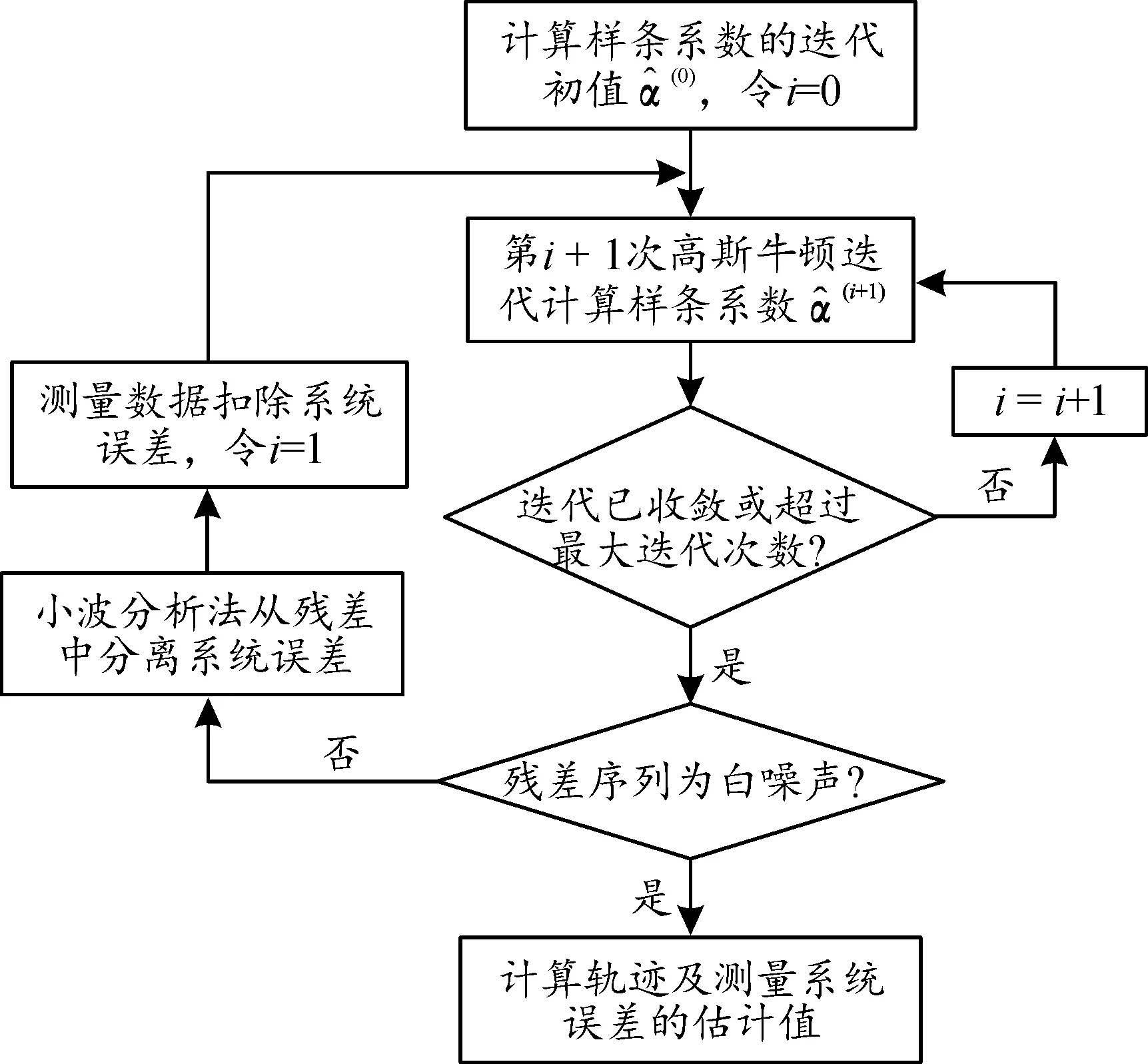
圖2 半參數估計方法的原理圖

具體步驟如下:

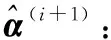
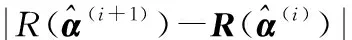
步驟4檢驗殘差ΔY是否為白噪聲,如果是,則轉到步驟6,否則,令j=j+1,轉到步驟5。

步驟5利用Daubechies7小波從殘差ΔY中分離出系統誤差ΔS(j)和測量噪聲,令Y=Y-ΔS(j),i=0,ω=1,轉到步驟2,重新利用高斯牛頓迭代法估計α。

2.2 估計精度分析

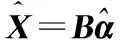
于是

即

BTAT(Y-F(Bαp))=0

(8)

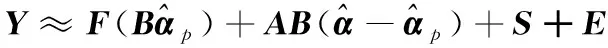
(9)

由式(8)和式(9)可得:

于是,參數估計方法的軌跡估計精度為

B(BTATAB)-1BT+QQT

(10)

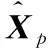
同理可得:

B(BTATAB)-1BT

(11)

即半參數估計方法得到的軌跡精度優于忽略系統誤差的參數估計方法的精度。

3 仿真實驗與結果分析

利用仿真實驗檢驗半參數估計方法的性能。飛行器的真實軌跡由6自由動力學仿真模型產生,時長為94 s,采樣率為20 Hz。5臺雷達(測量數據為距離和距離變化率)和2臺光學設備(測量數據為方位角和俯仰角)對飛行器跟蹤測量。利用測量設備的站址和飛行器的軌跡真值生成測量真值,在測量真值的基礎上通過疊加測量誤差生成仿真測量數據,其中,距離、方位角和俯仰角的測量誤差含有不可參數建模系統誤差的實測值,距離變化率測量誤差為均方根為0.05 m/s的隨機誤差。

分別采用參數估計方法和半參數估計方法對飛行器軌跡進行估計,其中,參數估計方法忽略距離、方位角和俯仰角的不可參數建模系統誤差的影響,而半參數估計方法對系統誤差進行分離。

通過比較軌跡估計值與真實值的差異得到軌跡的估計誤差,由估計誤差的大小分析估計方法的精度。t時刻的位置和速度估計誤差分別定義為

圖3和圖4分別是位置和速度估計誤差隨時間變化的曲線圖。可見,半參數估計方法相對參數估計方法關于位置和速度的估計精度都有較大幅度提高,參數估計方法對位置和速度估計的平均誤差分別為1.29 m和0.095 m/s,而半參數估計方法對位置和速度估計的平均誤差分別為0.62 m和0.055 m/s,與參數估計方法相比,半參數估計方法關于位置和速度的估計誤差分別減少了51.9%和42.1%。

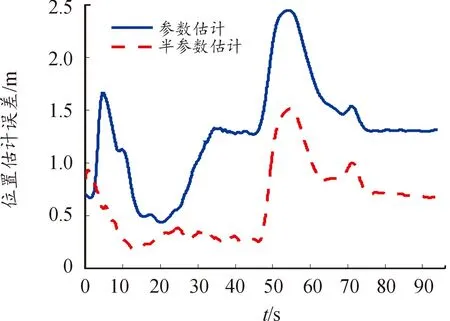
圖3 位置估計誤差

圖4 速度估計誤差

圖5是其中1臺雷達的距離測量誤差及半參數估計方法獲得的系統誤差估計結果。圖6是半參數估計方法分離出的隨機誤差。可見,系統誤差估計值的變化平緩,頻率較低,與測量誤差的變化趨勢相吻合,分離出的隨機誤差頻率較高,接近于白噪聲。圖7是其中1臺光學設備的俯仰角測量誤差及系統誤差估計結果。圖8是對應的隨機誤差分離結果,可見,半參數估計方法對光學設備系統誤差的分離效果也較好。圖7和圖8中的誤差曲線在45～75 s出現空白,這是因為該時段飛行器進入云層,光學設備丟失目標,沒有獲得測量數據。

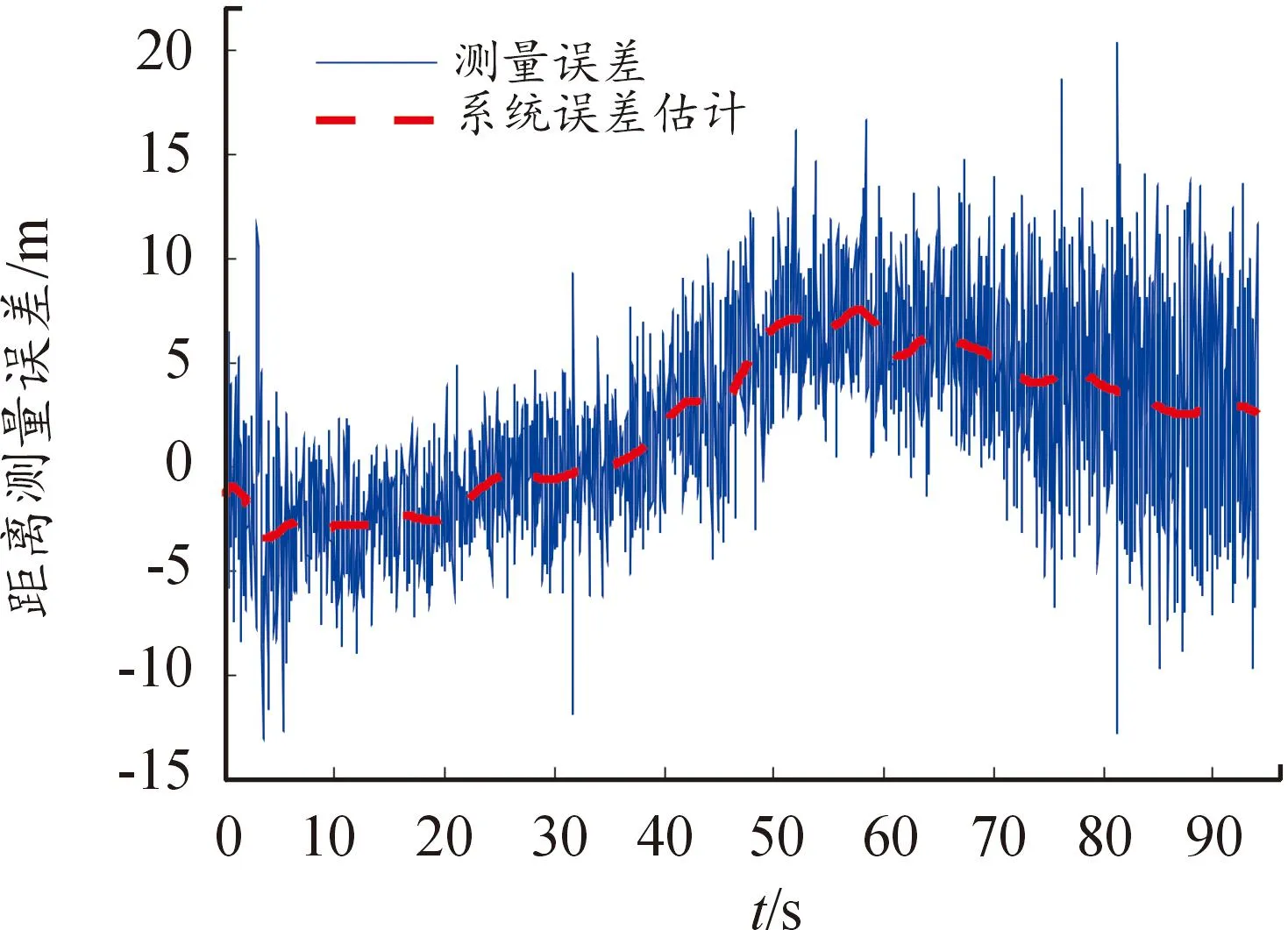
圖5 雷達距離測量誤差及系統誤差估計結果

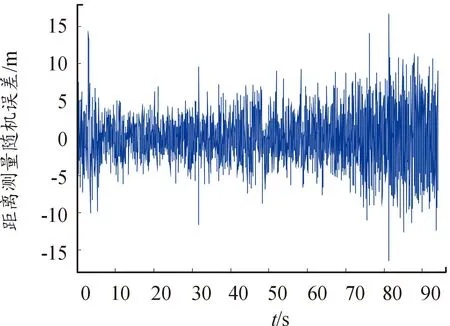
圖6 雷達距離測量隨機誤差的分離結果

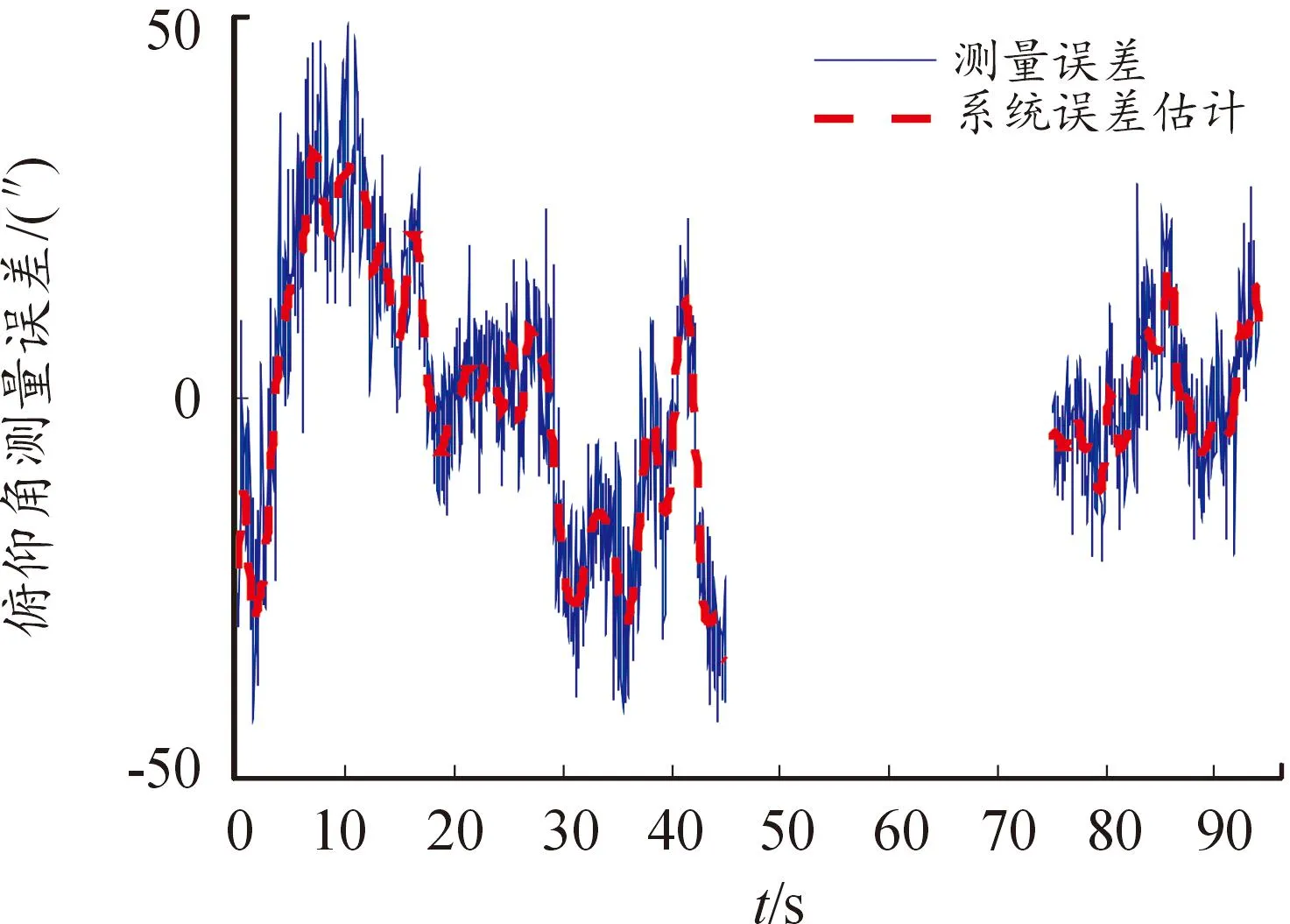
圖7 光學設備俯仰角測量誤差及系統誤差估計結果

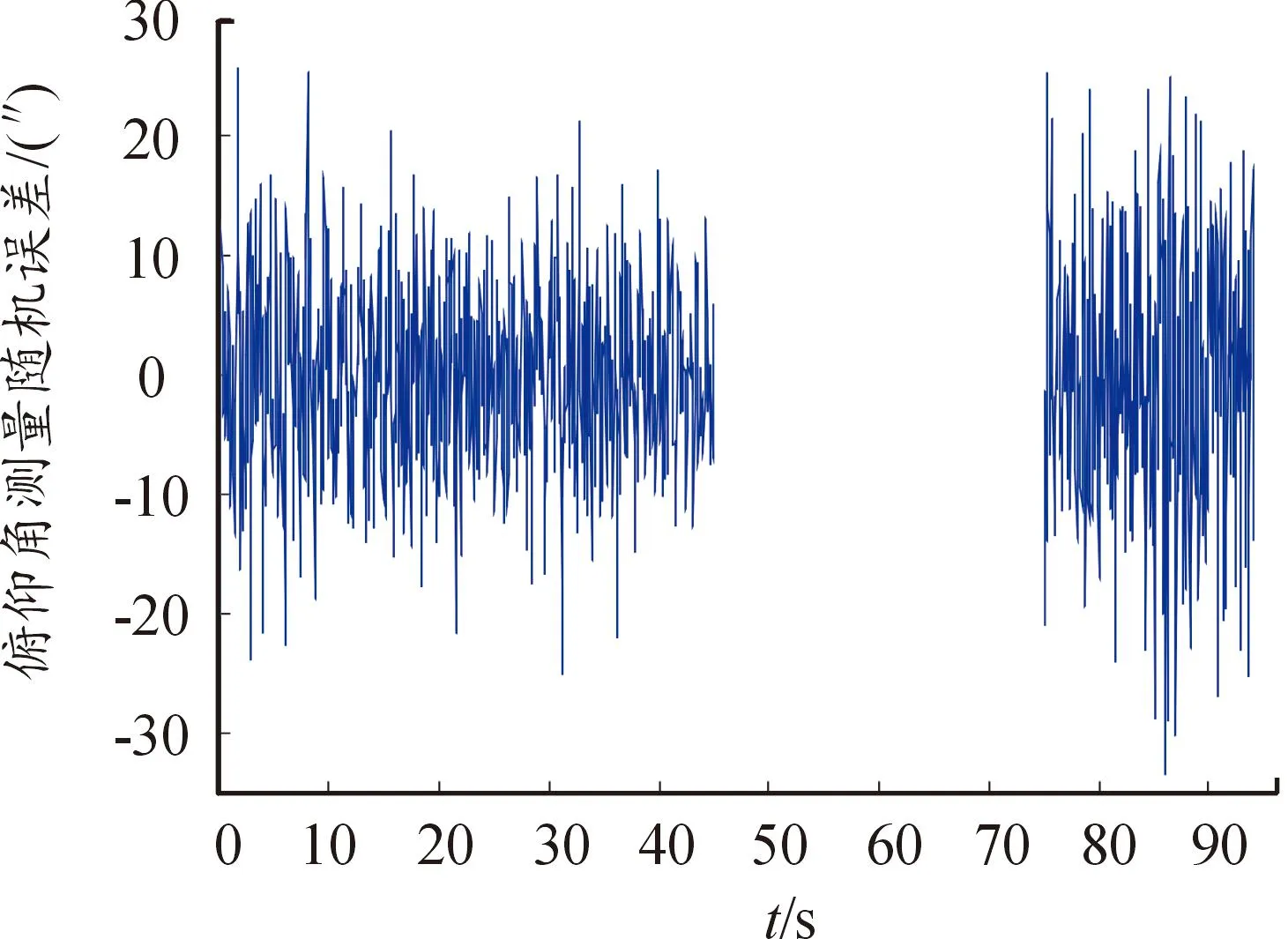
圖8 光學設備俯仰角測量隨機誤差的分離結果

4 結論

1) 提出了一種基于半參數回歸的飛行器軌跡估計新方法,可同時估計軌跡參數和分離不可參數建模的測量系統誤差,有效抑制了測量系統誤差對軌跡估計的影響,提高了軌跡估計精度。

2) 得到了半參數估計方法估計精度的理論公式,從理論上證明了半參數估計方法的精度優于傳統的參數估計方法。

3) 通過仿真實驗檢驗了半參數估計方法的軌跡估計精度,結果表明,半參數估計方法對飛行器位置和速度的估計精度相對參數估計方法都有大幅度的提高,系統誤差分離結果準確可靠,有效解決了不可參數建模系統誤差的處理難題,在飛行器試驗鑒定領域有重要應用價值。