水體透射光譜結(jié)合主成分分析(PCA)改進化學需氧量(COD)含量估算研究

王彩玲 位欣欣

(西安石油大學 計算機學院,西安 710065)

化學需氧量(Chemical Oxygen Demand,COD)是表征水體被還原性物質(zhì)污染程度的指標,該指標作為有機物相對含量的綜合指標之一,列入我國主要污染物總量控制指標,根據(jù)其排放濃度衡量水體污染程度[1]。傳統(tǒng)的COD測量方法主要是基于化學分析,耗時較長,操作專業(yè)性高,不利于快速、實時地獲取水體中COD的信息[2]。而高光譜技術(shù)結(jié)合人工神經(jīng)網(wǎng)絡模型可以快速、準確地估算水體中的COD含量,從而為環(huán)境監(jiān)測和水質(zhì)調(diào)控提供了有效手段。

近年來,關(guān)于利用高光譜遙感技術(shù)評價和監(jiān)測水資源水質(zhì)信息狀況方面的研究愈發(fā)深入[3]。高光譜技術(shù)是一種通過對目標物體光譜信息的收集和分析,實現(xiàn)對目標物體性質(zhì)的識別和定量測量的技術(shù)。利用高光譜技術(shù),可以實現(xiàn)對水體中COD含量的快速、無損檢測。國內(nèi)外學者利用高光譜技術(shù)結(jié)合各種算法進行了大量水質(zhì)檢測技術(shù)的研究。YES等[4]應用UVE-SPA-LS-SUV的方法實現(xiàn)了對COD的建模預測;KIMBERLY等[5]構(gòu)建出偏最小二乘最佳高光譜 Chl-a 濃度估算模型;ORTIZ等[6]利用高光譜技術(shù)檢測出水體總懸浮固體濃度;曹引等[7]建立偏最小二乘水體濁度高光譜反演模型,為水體濁度大面積遙感檢測提供了技術(shù)支持;張賢龍等[8]提出高光譜技術(shù)水質(zhì)參數(shù)濃度反演模型;蔡建楠等[9]采用 GA 遺傳算法實現(xiàn)了基于偏最小二乘法高光譜 COD 檢測模型的優(yōu)化。

本文以水體COD含量為研究對象,通過多元散射校正(MSC)、標準正態(tài)變換(SNV)、最大最小歸一化(MMN)三種不同的高光譜數(shù)據(jù)預處理方法對采集到的高光譜數(shù)據(jù)進行預處理,建立相應的高斯過程回歸模型(Gaussian Process Regression,GPR)和BP神經(jīng)網(wǎng)絡模型,并對模型進行改進。結(jié)合主成分分析(Principal Component Analysis,PCA)方法對預處理后的數(shù)據(jù)進行主成分分析,通過數(shù)據(jù)降維,保留足以解釋90% 的方差的成分,從預處理后的光譜數(shù)據(jù)中提取22個主成分,篩選出相關(guān)性較好的波段,建立改進的GPR水體COD含量估算模型和BP神經(jīng)網(wǎng)絡模型水體COD含量估算模型。實驗結(jié)果表明,基于PCA改進的模型的預測精度均明顯提高,其中標準正態(tài)變量變換特征PCA-BP神經(jīng)網(wǎng)絡模型的R2高達0.994 0,均方根誤差為0.022 540,模型性能最優(yōu),能夠?qū)崿F(xiàn)水體中COD含量的檢測。

1 實驗部分

1.1 光譜儀

實驗用儀器為 Ocean Optics 公司出品的 OCEAN-HDXXR 微型光纖光譜儀,該光譜儀采用高清晰度光學系統(tǒng),具有高通量、低雜散光和高熱穩(wěn)定性的特點,適用于精確測量溶液中的分析物,具有體積小,容易集成到許多工業(yè)應用的生產(chǎn)過程環(huán)境的優(yōu)勢。

1.2 透射光譜數(shù)據(jù)獲取

選擇配比溶液為 0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9、1.0 mg/L的 COD標準溶液,更換光譜儀的狹縫為 10 μm,相同時間間隔各自重復采集10次上述標準溶液200～1 030 nm的高光譜透射率數(shù)據(jù),共得到100條數(shù)據(jù)。

采用白板校正分別得到所采集的三種高光譜數(shù)據(jù)的光譜透射率值[10],如式(1)所示:

(1)

其中:Ro為原始光譜數(shù)據(jù),RW為白板數(shù)據(jù)。

2 實驗結(jié)果

2.1 COD原始透射光譜

圖1(a)為10種濃度COD原始透射光譜,從圖1中可以看出,不同濃度溶液的COD光譜曲線的趨勢類似,在紫外線波段180.1～400 nm,COD光譜曲線呈先下降后上升的趨勢,這說明隨著有機物含量的增加,水體COD含量越低,其光譜曲線特征越發(fā)明顯。

圖1 透射光譜圖Figure 1 Transmission spectrograms.

2.2 數(shù)據(jù)預處理

對于高光譜數(shù)據(jù),除了COD的特征信息外,還可能有光譜采集過程中產(chǎn)生的背景噪聲輻射以及信號轉(zhuǎn)換過程中產(chǎn)生的附加噪聲[11],分別采用不同的預處理方法進行處理,如圖1(b)～1(d)所示。其中,采用多元散射校正有效消除由于散射水平不同導致的光譜數(shù)據(jù)的差異,增強光譜與數(shù)據(jù)之間的相關(guān)性[12];采用標準正態(tài)變量變換降低固體顆粒大小、表面散射以及光源變換等對光譜信息的影響[13];采用最大最小歸一化在不同程度上消除了光譜散射和背景干擾的影響[13]。

2.3 模型的建立

采用高斯過程回歸模型和BP神經(jīng)網(wǎng)絡模型以上述預處理后的高光譜數(shù)據(jù)為自變量,將不同濃度的COD樣本與光譜數(shù)據(jù)進行擬合,為了防止在模型的訓練過程中出現(xiàn)過擬合的現(xiàn)象,采用五折交叉驗證方法。輸入為光譜數(shù)據(jù),輸出為COD樣本的濃度。然后分別建立各類自變量的高斯過程回歸模型和BP神經(jīng)網(wǎng)絡模型。

2.3.1 高斯過程回歸模型建立

高斯過程回歸(GPR)是一種建立在貝葉斯框架下的統(tǒng)計學習方法,模型性質(zhì)完全由均值函數(shù)和協(xié)方差函數(shù)確定[14]。它有嚴格的統(tǒng)計學理論基礎(chǔ),對處理高維數(shù)、小樣本、非線性等復雜回歸問題具有良好的適應性[14];該算法還具有容易實現(xiàn),參數(shù)自適應獲取,輸出結(jié)果具有概率意義等優(yōu)點[14]。

將預處理后的透射光譜數(shù)據(jù)作為模型的輸入,建立高斯過程回歸模型。使用MATLAB中自帶的 Quadratic Rational Gaussian Process Regression算法對高斯過程回歸模型進行學習訓練。本次實驗中將該算法的基函數(shù)設置為常量,核函數(shù)選用二次有理函數(shù),同時在訓練過程中對高光譜數(shù)據(jù)進行標準化,優(yōu)化數(shù)值參數(shù),以達到最優(yōu)效果。模型輸出結(jié)果如圖2所示。

圖2 高斯過程回歸模型預測結(jié)果Figure 2 The prediction results of Gaussian process regression model.

2.3.2 BP神經(jīng)網(wǎng)絡模型建立

使用MATLAB中自帶的 Scaled Conjugate Gradient Backpropagation算法對 BP 模型進行學習訓練。該算法根據(jù)縮放共軛梯度法更新權(quán)重和偏差值,同時占用更少的內(nèi)存,適用于高光譜數(shù)據(jù),選擇三層神經(jīng)網(wǎng)絡模型進行訓練,第一層神經(jīng)元個數(shù)設置為20,第二、三層設置為10,該算法中迭代次數(shù)(Epoch)閾值為 1 000,激活函數(shù)設置選用Sigmoid函數(shù),探究不同預處理方法對BP網(wǎng)絡模型回歸準確率影響。模型輸出結(jié)果如圖3所示。

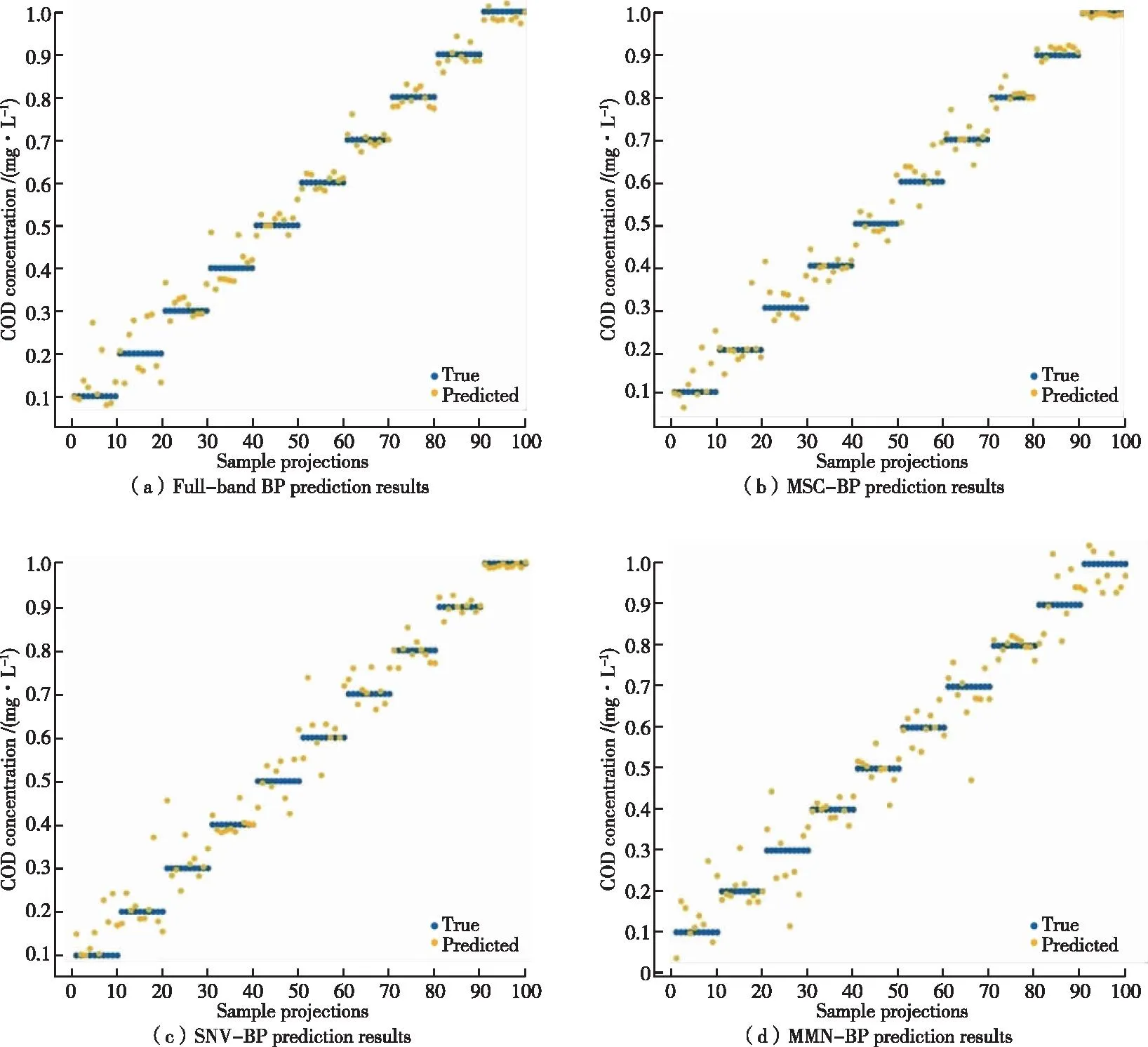
圖3 BP神經(jīng)網(wǎng)絡模型預測結(jié)果Figure 3 The prediction results of BP neural network model.

2.3.3 模型結(jié)果評估

以均方根誤差RMSE和決定系數(shù)R2為標準對所建立的各個模型進行精度檢驗與比較。其中:均方根誤差RMSE越小,說明模型選擇和擬合更好;決定系數(shù)R2越接近1,說明模型擬合的效果越好。檢驗結(jié)果如表1所示。

表1 未改進模型精度檢驗結(jié)果Table 1 Testing results of unimproved model accuracy

由表1可知,與全波段的模型相比,經(jīng)過預處理后的二次有理GPR模型和BP神經(jīng)網(wǎng)絡模型的性能均有所提高。其中,預處理后的二次有理GPR模型其R2最高達0.982 6;其RMSE最低為0.038 168;預處理后的BP神經(jīng)網(wǎng)絡其R2最高達0.979 3,比全波段R2高出0.039 2,其RMSE最低為0.041 567;與全波段的模型相比,預測精度均比原數(shù)據(jù)較高。說明采用預處理方法對數(shù)據(jù)進行處理可以有效提取有效光譜信息,排除干擾信息,從而提高光譜數(shù)據(jù)與 COD濃度之間的相關(guān)性,使得模型的性能提高,預測效果更好。

2.4 基于PCA改進模型的建立

利用主成分分析法(PCA)對模型進行改進,建立基于PCA的BP神經(jīng)網(wǎng)絡定量估算模型以及二次有理GPR的定量估算模型。PCA是一種使用最廣泛的基于線性映射的特征提取技術(shù),該算法通過一定的變換將高維數(shù)據(jù)映射到一個新的低維空間,使得任何數(shù)據(jù)投影的第一大方差在第一個坐標(稱為第一主成分)上,第二大方差在第二個坐標(第二主成分)上,依此類推,這些主成分能夠反映絕大部分的變量信息[15]。本文實驗中設置PCA保留足以解釋90% 方差的成分。模型訓練后,提取22個主成分。每成分的解釋方差(順序排列):37.0%、 18.4%、9.1%、4.3%、3.0%、2.0%、1.7%、1.5%、1.4%、1.3%(隱藏最不重要成分的方差)。

2.4.1 基于PCA改進的高斯回歸模型

將 COD數(shù)據(jù)集作為PCA-二次有理GPR模型的輸入。模型輸出結(jié)果如圖4所示。

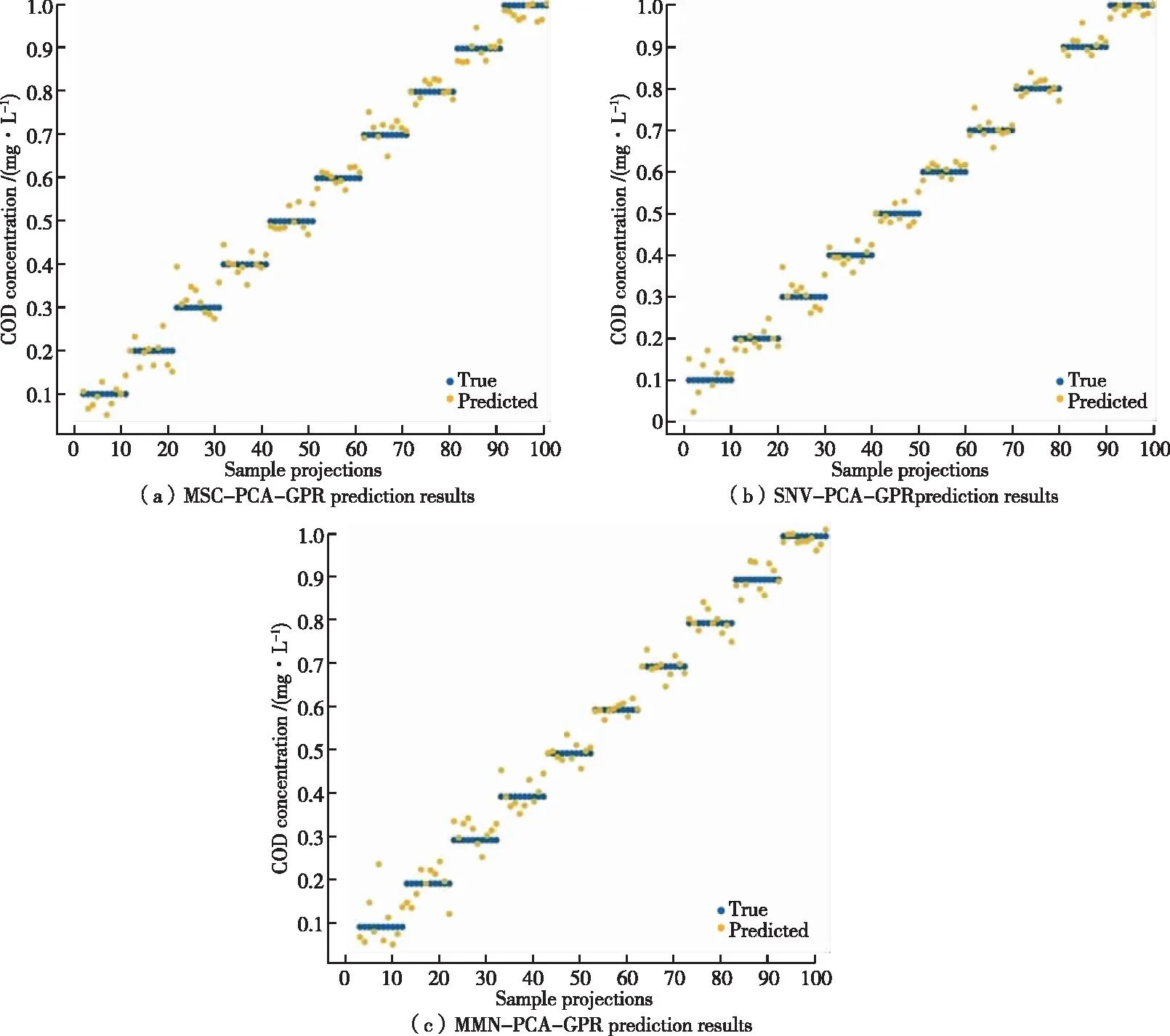
圖4 改進的高斯回歸模型預測結(jié)果Figure 4 The prediction results of improved Gaussian regression model.

2.4.2 基于PCA改進的BP神經(jīng)網(wǎng)絡模型

將 COD數(shù)據(jù)集作為PCA-BP神經(jīng)網(wǎng)絡模型的輸入。模型輸出結(jié)果如圖5所示。

圖5 改進的BP神經(jīng)網(wǎng)絡預測結(jié)果Figure 5 The prediction results of improved BP neural network model.

2.4.3 基于PCA改進的模型結(jié)果評估

從輸出的結(jié)果可以看出,預測值與真實值差異較小,具有很好的相關(guān)性。對所建立的各個改進的二次有理GPR模型以及 BP神經(jīng)網(wǎng)絡模型進行精度檢驗并進行比較。改進模型檢驗結(jié)果如表2所示。

表2 改進的模型精度檢驗表Table 2 Testing results of improved model accuracy

由表2可知,與未改進的模型相比,基于PCA改進模型的預測精度均有所提高。其中,多元散射校正特征PCA-二次有理GPR模型的R2增長為0.990 9,多元散射校正特征PCA-BP神經(jīng)網(wǎng)絡模型的R2增長為0.990 8,其RMSE均有所減少;標準正態(tài)變換特征PCA-二次有理GPR模型的R2增長為0.992 0,標準正態(tài)變量變換特征PCA-BP神經(jīng)網(wǎng)絡模型的R2增長為0.994 0,可以發(fā)現(xiàn)改進后的標準正態(tài)變量變換的R2更接近于1,且RMSE均明顯減少,精度較為提高;最大最小歸一化特征PCA-二次有理GPR模型和最大最小歸一化特征PCA-BP神經(jīng)網(wǎng)絡模型的R2增長為0.988 3和0.984 4;其RMSE減少為0.031 195和0.036 048,預測精度相比未改進的模型也有所提升。說明采用 PCA對預處理后的數(shù)據(jù)進行數(shù)據(jù)降維,可以實現(xiàn) COD含量估算模型的優(yōu)化。

3 結(jié)論

分別采用多元散射校正、標準正態(tài)變量變換、最大最小歸一化對光譜透射率數(shù)據(jù)進行預處理,并建立二次有理高斯回歸模型和BP神經(jīng)網(wǎng)絡模型,對于不同的模型,探究不同特征輸入對模型精度的影響,結(jié)果表明:3種預處理方法可以有效降低噪音對數(shù)據(jù)的干擾,且二次有理GPR模型相比BP神經(jīng)網(wǎng)絡模型有較好的預測精度;基于PCA對各預處理后的透射光譜數(shù)據(jù)進行數(shù)據(jù)降維,篩選出相關(guān)性較好的波段,從而建立改進的二次有理GPR模型和BP神經(jīng)網(wǎng)絡模型。其中,標準正態(tài)變量變換特征PCA-BP神經(jīng)網(wǎng)絡模型決定系數(shù)達到了0.994 0,均方根誤差為0.022 540,依據(jù)R2最大、RMSE最小原則,采用PCA改進的標準正態(tài)變量變換特征BP神經(jīng)網(wǎng)絡模型可以建立精度較好的COD定量估算模型。