基于反步法控制器的雙缸液壓系統同步運動控制研究

劉海星， 劉凱磊，，3， 強紅賓，， 康紹鵬， 殷鵬龍

（1.江蘇理工學院機械工程學院， 江蘇常州 213001； 2.國機重工集團常林有限公司，江蘇常州 213136； 3.江蘇大學流體機械工程技術研究中心， 江蘇鎮江 212013）

0 前言

大型鍛件在冶金機械、 電力設備、 兵器、 航空航天工業、 石油化工、 艦船制造、 重型車輛等裝備中有著廣泛應用［1］。 隨著鍛造液壓機加工精度的提高，對鍛造液壓機雙缸同步控制精度的要求也不斷提高，目前， 已有許多學者開展了相關的研究工作［2－4］。 李勝永［5］設計了誤差反饋的同步控制結構， 提高了同步控制精度。 李海軍等［6］設計了灰色預測前饋控制器，該控制器能夠控制雙液壓缸的同步誤差保持在15 mm內。 張兵等人［7］針對強非線性和強耦合作用嚴重影響雙缸同步系統控制精度的問題， 提出基于內力補償和位置補償的自由度控制策略， 通過仿真分析驗證了該策略的有效性。 吳娜、 袁名偉［8］使用模糊－單神經元PID 控制算法， 通過仿真與實驗驗證了該算法的可行性。 薛召等人［9］針對傳統PID 控制器同步控制穩定性不高的問題， 提出一種基于模糊單神經元PID 復合算法的雙缸耦合同步控制策略， 通過仿真與實驗證明該控制策略的合理性。 劉愛玲等［10］針對雙液壓缸同步控制的問題， 基于模糊控制理論提出了模糊前饋控制器。

然而， 鍛造液壓機液壓系統存在活塞摩擦、 液控元件等因素會造成液壓損失［6］； 再者， 鍛件位置、 形狀、 大小、 溫度等因素會導致兩液壓缸受力不一致［11］， 這些內在和外在因素會導致雙缸同步控制精度降低， 不能滿足鍛造液壓機工況的需求。

因此， 針對鍛造液壓機雙缸同步控制精度不足的問題， 本文作者以傳統雙缸同步控制系統為研究對象， 建立液壓缸位置控制系統運動學模型， 結合Lya?punov 穩定性理論， 設計基于模型的反步法控制器，并將該控制器應用到并聯型同步控制結構中， 同時采用AMESim 和Simulink 構建雙缸同步控制仿真模型，并將反步法控制器與PID 控制器進行仿真比較分析，為后續試驗研究提供理論依據。

1 雙缸同步控制系統組成

傳統的鍛造液壓機雙缸同步系統是由油源、 兩個三位四通比例閥、 兩個液壓缸、 活動橫梁組成。 文中對傳統的大型液壓機雙缸同步系統進行改動， 在液壓缸1 與液壓缸2 左端右端各增加壓力傳感器， 在液壓缸1 與液壓缸2 活塞桿處各增加速度傳感器、 力傳感器、 位移傳感器， 如圖1 所示。

根據圖1 對控制過程進行簡要說明： 首先油源對該系統提供壓力， 在對液壓缸1 和2 提供指定位移信號后， 控制器將收集到位移傳感器1 和2 的位移信號、 速度傳感器1 與2 的速度信號、 力傳感器1 與2的力信號、 無桿腔壓力傳感器1 與2 的壓力信號、 有桿腔壓力傳感器1 與2 的壓力信號， 隨后控制器會控制三位四通比例換向閥1 和2 動作， 對液壓缸1 和2進行油液補充和減少， 從而調整液壓缸1 和2 活塞桿位移， 實現同步控制［5］。 控制的關鍵在于控制信號與傳感器信號之間建立一種閉環反饋機制， 能夠實現實時的液壓系統變量調控， 以保障同步運行的精確度［12］。

2 位置控制系統運動學模型建立

液壓缸位置控制系統運動學模型建立以液壓缸1為例， 對其簡化如圖2 所示。 圖中：ps為三位四通比例閥進口壓力；pr為系統回油壓力（一般設為0）；p1為液壓缸無桿腔壓力；p2為液壓缸有桿腔壓力；Q1、Q2分別為流入和流出三位四通換向閥的流量；FL是液壓缸承受的外負載力。

對該系統做以下假設：

（1） 假設ps是恒壓源， 以ps的壓力為系統供油；

（2） 系統中采用的比例方向閥為理想對稱滑閥且具有零遮蓋窗口；

（3） 比例方向閥的節流面積和節流閥口大小呈線性關系。

結合文獻［13］的研究可建立電液伺服系統運動學模型為

式中：m為系統負載質量， kg；x1為液壓缸輸出位移， m；x2為液壓缸輸出速度， m/s；A1為液壓缸無桿腔工作面積， m2；A2為液壓缸有桿腔工作面積，m2；V01為液壓缸無桿腔初始容積， m3；V02為液壓缸有桿腔初始容積， m3；Ct為執行器泄漏系數；βe為液壓油彈性模量；G為系統負載重力， N。

根據文獻［13］可知比例閥動態方程可近似為

式中：τv、ki、u分別為比例閥時間常數、 閥芯電流增益及控制輸入。 為了減小推導的復雜性， 簡化比例閥動態環節， 即

為了使伸出或者縮回工況的流量方程合并成為一個方程， 定義變量s， 根據式（4） 可以通過輸入值的正負對變量s的值做出調整， 即：

結合式（3） （4）， 根據文獻［13］可以列出流量方程如下所示：

式中：xv為閥芯位移；kq為流量系數， 展開為

式中：Cd為比例閥節流孔流量系數；w1、w2分別為比例閥閥芯節流孔左右兩端面積梯度；ρ為液壓油密度。 由于該三位四通比例閥是對稱滑閥，kq1＝kq2＝kq， 同時也是一個定值。

令

先將式（10） 進行求導， 將式 （11） — （14）代入式（1） 中可以簡化運動學模型為

從推導過程可以看出， 液壓缸位移受到該運動學模型參數的影響， 從式（15） 中可以發現輸入u控制x3的變化，x3控制x2的變化，x2控制x1的變化， 于是可以將式（15） 看成是從u至x1的3 個積分組成的串聯積分系統。 所以作者從式 （15） 入手， 結合Lyapunov 穩定性理論， 研究基于模型的反步法控制器。

3 反步法控制器的建立

反步設計法是交叉選擇Lyapunov 函數與反饋控制的遞歸過程， 是將整個系統的設計問題分解為一系列低階子系統的設計方法［14］。

首先定義：

其中：x1d是指定位移；x2d與x3d是虛擬控制量。

第一步， 為了使誤差e1趨近于0， 定義一個半正定Lyapunov 函數為

第二步， 為了使得e2趨近于0， 需要找到一個Lyapunov 函數包括e1和e2， 只有這2 個參數全部趨近于0， 系統才穩定。 定義半正定Lyapunov 函數：

第三步， 為了使得e3趨近于0， 需要找到一個Lyapunov 函數包括e1、e2和e3， 只有這3 個參數全部趨近于0， 系統才穩定。 定義半正定Lyapunov 函數：

從式（21） （28） （35） 可以看出控制輸入量u由模型參數、 指令變量以及參數k1、k2、k3決定， 控制輸入量u能夠根據模型參數的變化實時調整， 可以通過調整參數k1、k2、k3對活塞桿位移屬性進行控制。

4 雙缸同步控制系統策略制定

目前， 串聯型與并聯型同步控制結構在同步控制中較為常用［5］， 考慮到文中控制算法的獨立性， 采用并聯型雙缸同步控制結構， 如圖3 所示。

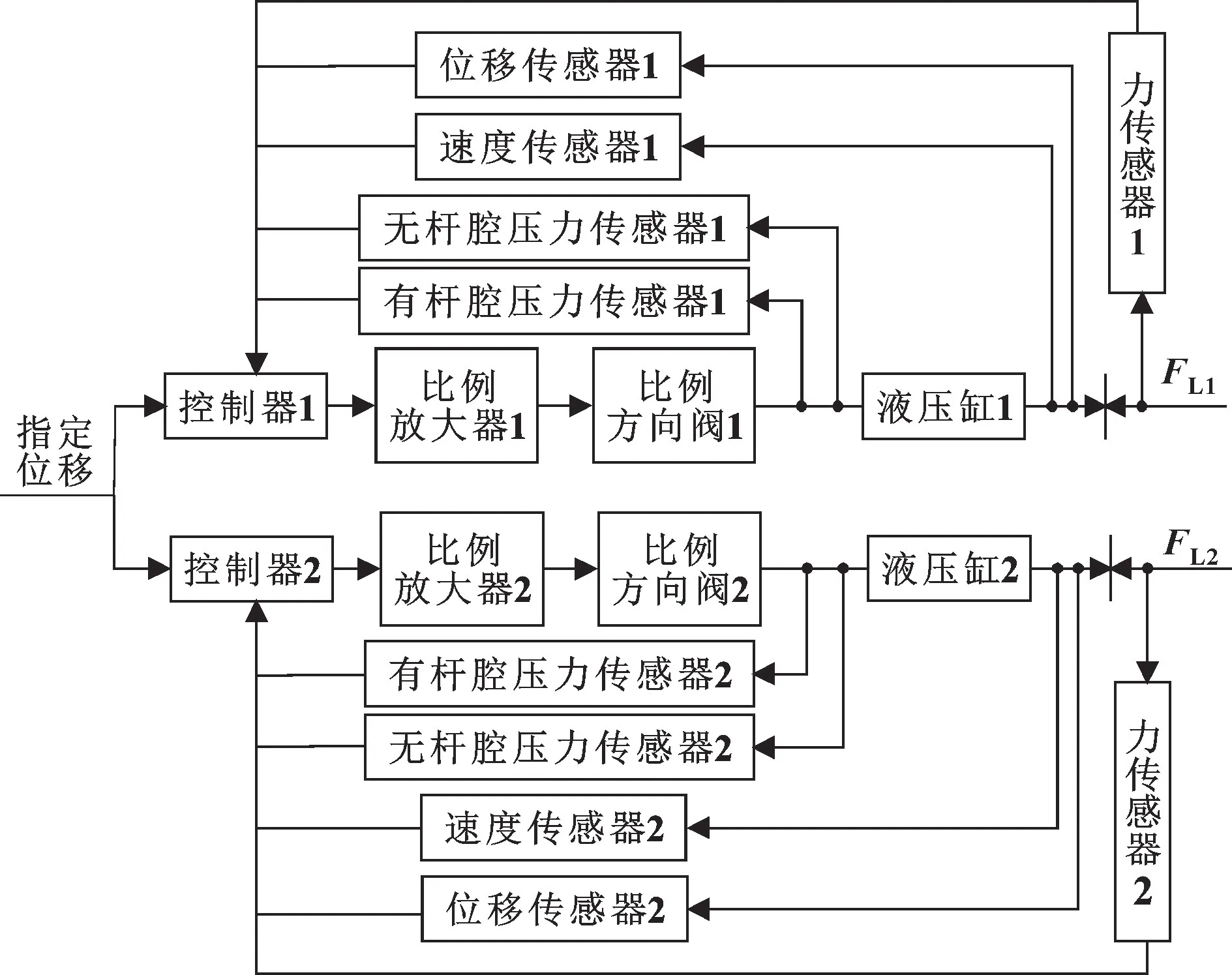
圖3 雙缸同步控制結構Fig.3 Double－cylinder synchronous control structure

從圖3 中可以看出， 給定控制器1 與2 位移信號， 控制器1 與2 將采集力傳感器1 與2、 速度傳感器1 與2、 位移傳感器1 與2、 無桿腔壓力傳感器1與2、 有桿腔壓力傳感器1 與2 的信號。 經過反步法計算， 向比例放大器1 與2 施加控制信號， 比例放大器1 與2 將控制信號放大控制比例方向閥1 與2 的動作， 補充或減少液壓缸1 與2 油液。

5 聯合仿真模型建立

5.1 設置前準備

在建立聯合仿真前， 首先需要確定相關設置， 確保聯合仿真能夠順利完成［15］， 具體如下：

（1） 模型搭建。 根據圖1 采用AMESim 軟件搭建液壓系統模型， 采用Simulink 軟件搭建控制器模型，采用S－function 模塊將算法封裝。

（2） 仿真接口搭建。 根據前面所述， 可以確定液壓系統向控制器反饋10 個信號變量， 控制器對液壓系統輸出2 個控制信號， 根據輸入輸出信號數量搭建聯合接口。

5.2 AMESim－Simulink 聯合仿真模型

將設置好的聯合仿真接口與AMESim 雙缸液壓模型和Simulink 控制器模型進行連接， 完成最終的鍛造液壓機雙缸同步控制系統聯合仿真模型， 如圖4 和圖5 所示， 聯合仿真主要參數如表1 所示。

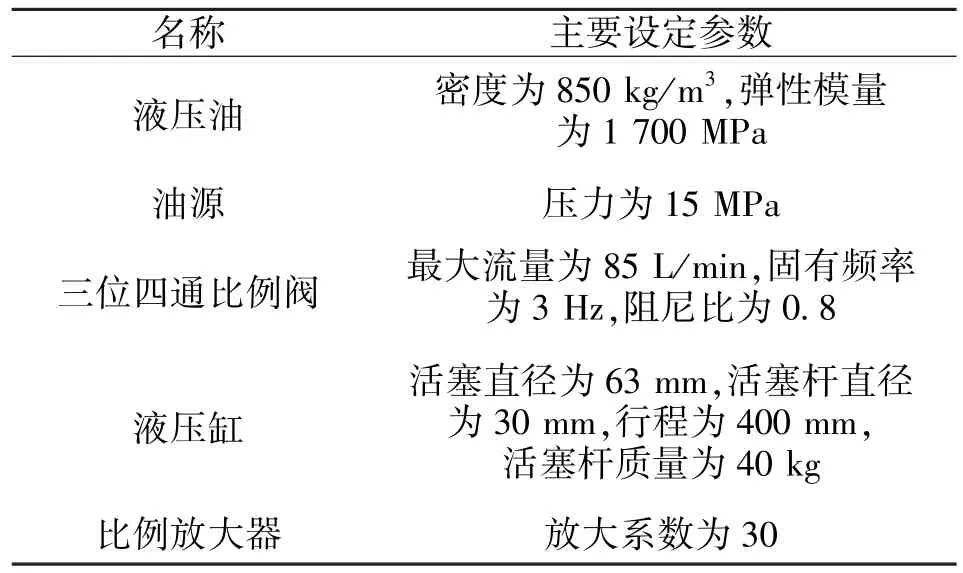
表1 聯合仿真主要參數Tab.1 Main parameters of joint simulation

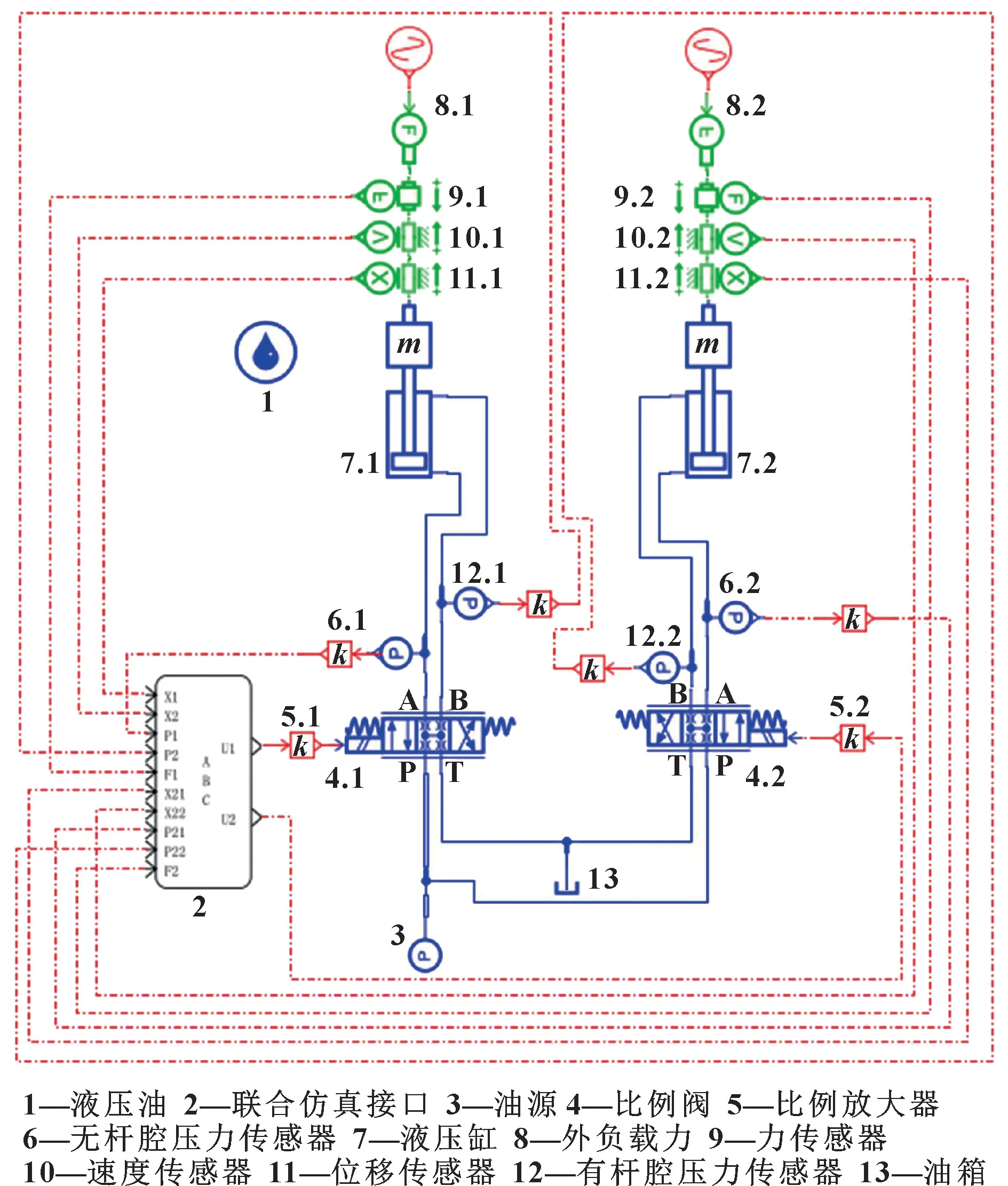
圖4 AMESim 仿真模型Fig.4 AMESim simulation model

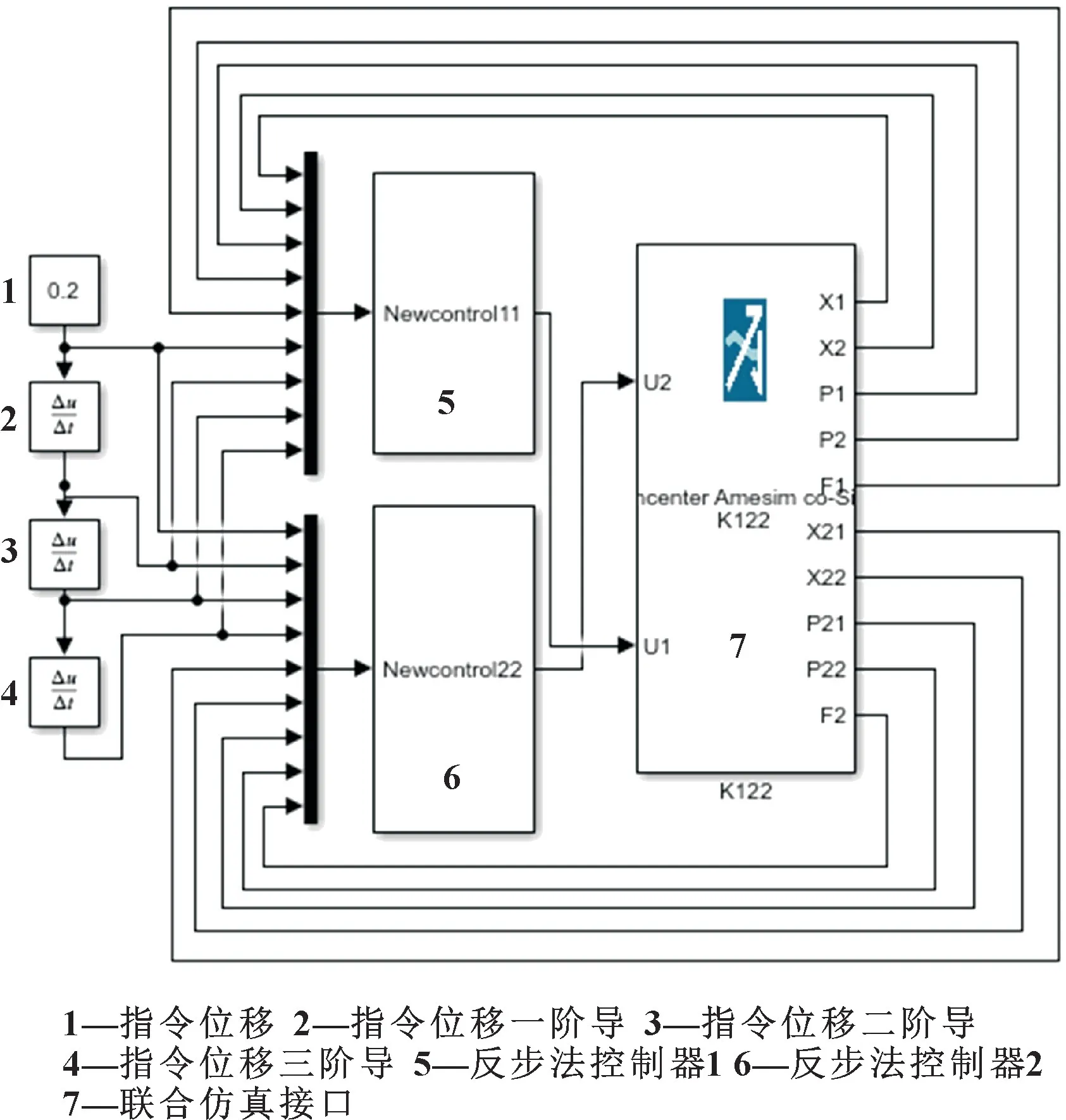
圖5 Simulink 仿真模型Fig.5 Simulink simulation model

6 聯合仿真

6.1 液壓缸位置控制系統數學模型辨識

為了驗證反步法控制器的性能， 采用PID 控制器進行對比， 為此需要建立系統輸入與輸出的數學模型以整定PID 控制器的3 個參數。

采用閉環辨識的方式辨識活塞桿移動至0.2 m 的傳遞函數， 因仿真軟件中獲得輸入與輸出的數據難度較低， 可以采用直接辨識方式， 采集活塞桿0 ～0.2 m、 0.2～0.4 m 內辨識對象輸入與輸出值， 采集時間為0.001 s。

已知比例放大器放大系數為30， 可以直接得出比例放大器數學模型為

式中：i為電流， A； Δu為輸入電壓， V。

（1） 比例換向閥傳遞函數辨識

采集0 ～0.2 m 內輸入電流與閥芯位移數據， 將它導入至MATLAB 系統辨識工具箱中進行辨識， 根據文獻［4］列舉的傳遞函數結構， 可選擇分母階次為2、 分子階次為0 的傳遞函數類型， 運行工具箱得到傳遞函數為

（2） 比例閥芯位移與液壓缸活塞桿傳遞函數辨識

采集0～0.2 m 內閥芯位移與活塞桿移動速度數據， 將其導入MATLAB 系統辨識工具箱中進行辨識，根據文獻［4］列舉的傳遞函數結構， 可選擇分母階次為2、 分子階次為0 的傳遞函數類型， 運行工具箱得到閥芯位移與活塞桿速度傳遞函數， 再乘以積分的時域函數， 得到閥芯位移與活塞桿位移傳遞函數為

對于液壓缸縮回工況， 設置液壓缸初始位置為0.4 m， 指令位移給定0.2 m， 采集活塞桿在0.2～0.4 m 內的輸入輸出值， 辨識方式與活塞桿伸出工況辨識方式相同， 得閥芯位移與活塞桿位移傳遞函數為

6.2 控制參數設定

首先采用粒子群算法對PID 控制器參數進行整定， 式（36） （37） （38） （39） 參與整定。 系統采用種群規模m＝200， 迭代次數n＝20， 慣性權重值w＝1， 學習因子c1＝2， 學習因子c2＝2。 以時間誤差絕對值積分性能作為參數尋優的適應度函數， 如式（40） 所示：

經過200 粒子的20 次迭代， 可獲得液壓缸活塞桿2 種狀態下參數整定結果， 如表2 所示。

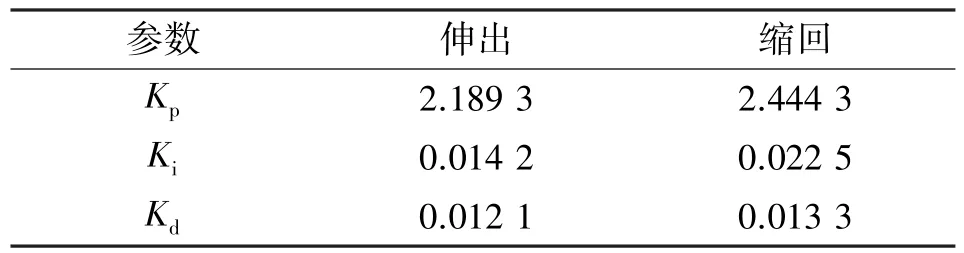
表2 PID 控制器整定參數Tab.2 PID controller tuning parameters

目前對于反步法參數整定的研究較少， 所以此次采用多次調試的方式得出反步法參數， 如表3 所示。

表3 反步法控制器參數Tab.3 Parameters of backstepping controller

6.3 仿真對比

為了驗證反步法控制器在雙缸同步控制中的性能， 從階躍響應和正弦響應入手進行仿真測試。

為了測試反步法控制器階躍響應性能， 給定位移信號0.2 m， 液壓缸1 處無外負載力， 對液壓缸2 施加4 600 N 的外負載力， 與PID 控制器控制的雙缸同步控制仿真模型進行對比， 運行結果如圖6—9 所示，仿真結果如表4 所示。

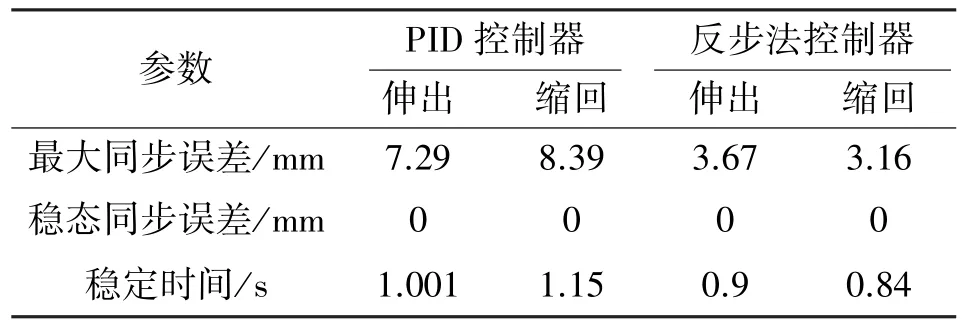
表4 同步控制仿真結果對比Tab.4 Comparison of simulation results for synchronous control

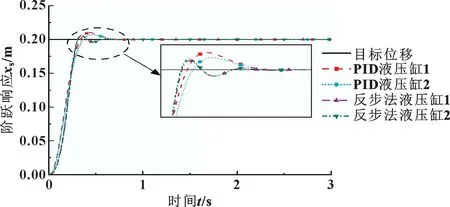
圖6 伸出工況階躍響應曲線Fig.6 Step response curves under extended operating condition

從圖6 和圖8 中可以看出： 從雙缸的超調量與到達指定位置的速度方面講， 反步法控制器均優于PID控制器； 從同步控制方面講， 結合圖7 與表4 可以得出， 在伸出工況中， 使用反步法控制器的雙缸同步控制最大誤差比PID 控制器減小了49.7%， 穩定時間減少了10.1%； 結合圖9 與表4 可以得出， 在縮回工況中， 使用反步法控制器的雙缸同步控制最大誤差比PID 控制器減小了62.3%， 穩定時間減少了26.96%，2 種控制器都能將穩態誤差控制在0 mm。

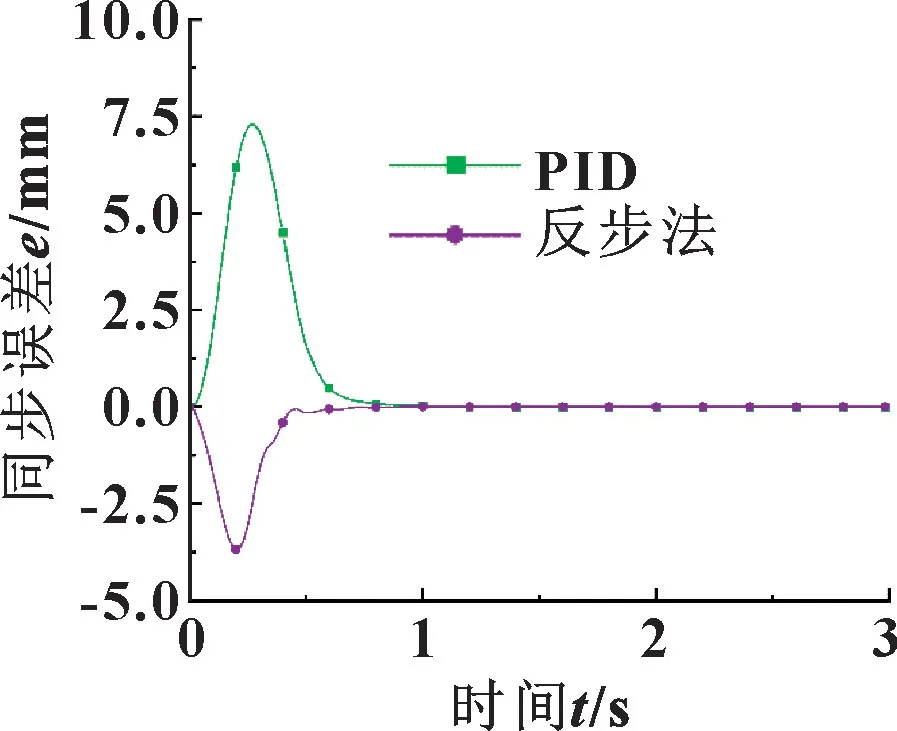
圖7 伸出工況同步誤差曲線Fig.7 Synchronous error curves under extended operating condition

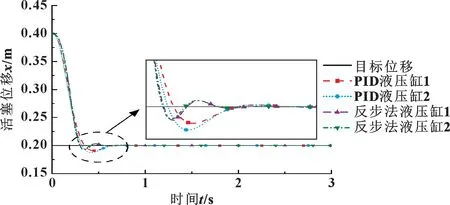
圖8 縮回工況階躍響應曲線Fig.8 Step response curves under retraction condition

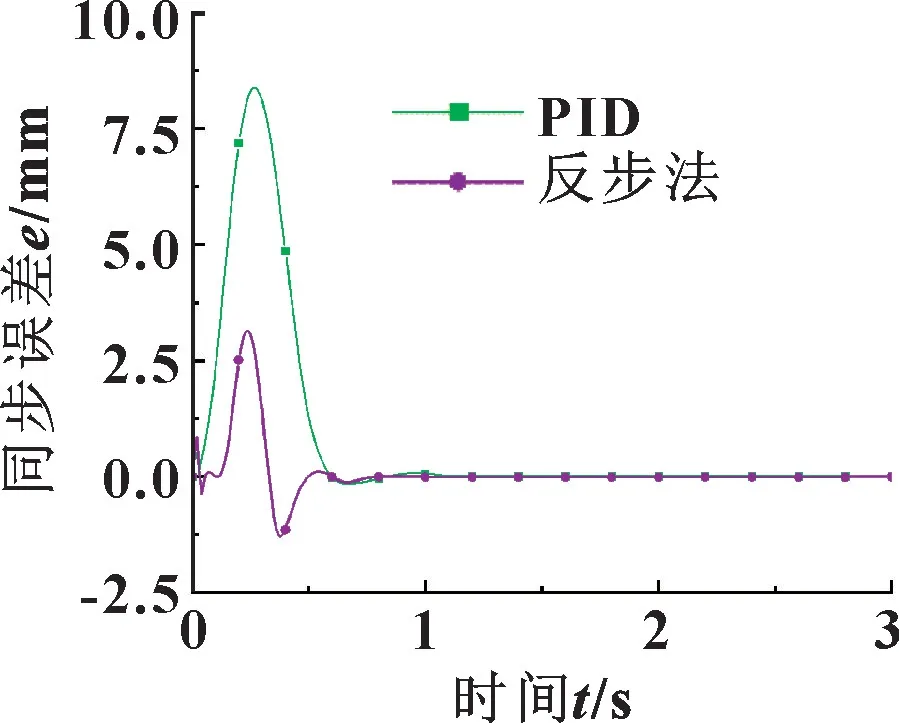
圖9 縮回工況同步誤差曲線Fig.9 Synchronization error curves of retraction condition

為了測試反步法控制器雙缸同步正弦響應性能，給定一個正弦的位置信號， 幅值為0.1 m， 在0.2 m處上下波動， 設定缸1 無外負載力， 缸2 外負載力為4 600 N， 與PID 控制器參與的雙缸同步控制仿真模型進行對比， 得出運行結果圖10 所示。 可以看出：反步法控制器控制的雙缸具有優越的跟蹤能力， 其滯后性遠遠低于PID 控制器。

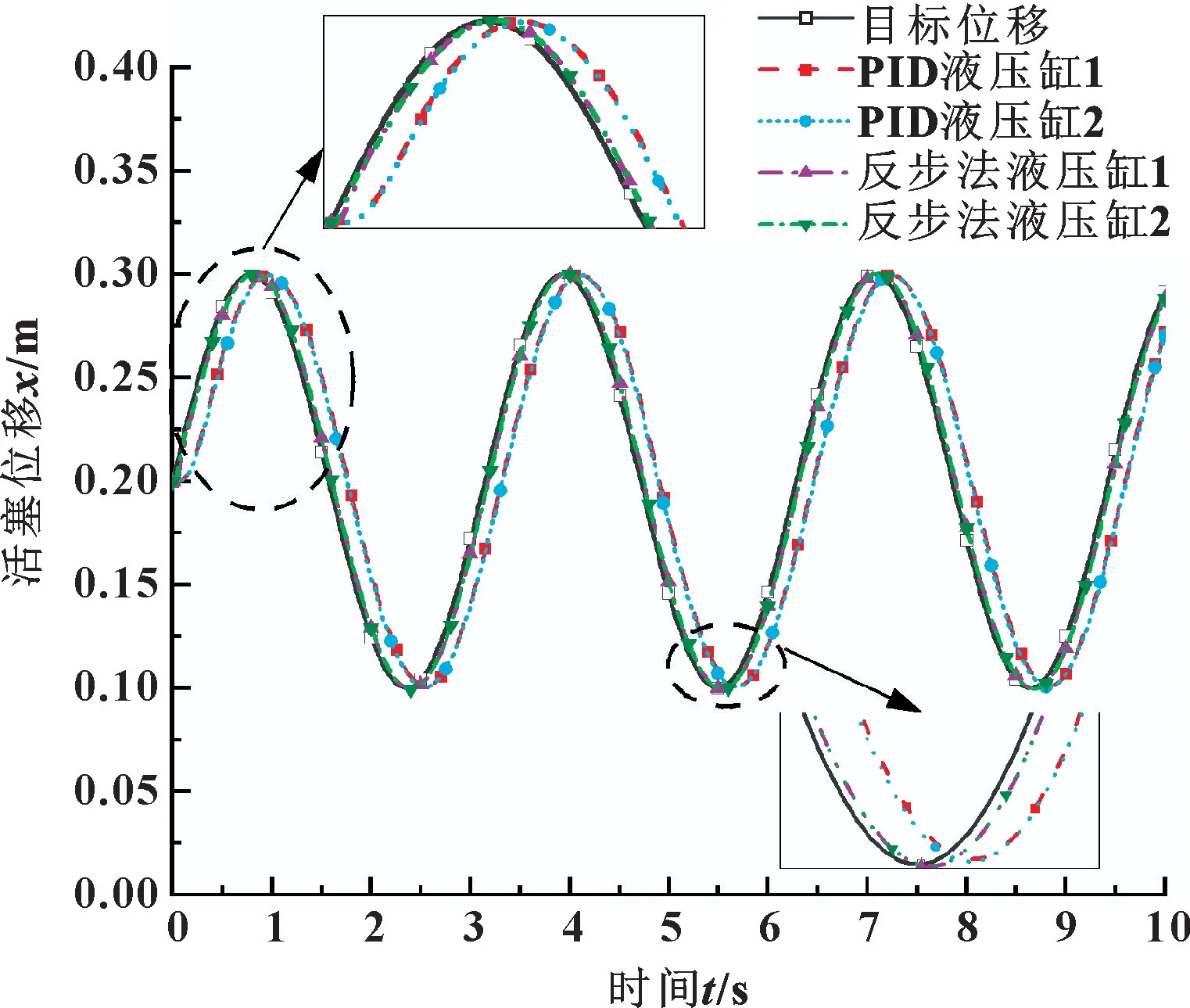
圖10 正弦響應曲線Fig.10 Sine response curves

7 結論

為了提高鍛造液壓機雙缸同步控制控制精度， 基于傳統雙缸同步控制系統， 分析了液壓缸位置控制系統運動學模型， 結合Lyapunov 穩定性理論， 設計了基于模型的反步法控制器， 并且應用于并聯同步控制結構中， 使用AMESim 與Simlink 聯合仿真的方式對反步法控制器與PID 控制器在雙缸同步控制中的性能進行對比， 主要得出以下結論： 反步法控制器在雙缸同步控制中的表現從階躍響應方面看， 活塞桿伸出時， 反步法控制器的最大同步誤差比PID 控制器最大同步誤差減小了49.7%， 調定時間減少了10.1%；在活塞桿縮回時， 反步法控制器的最大誤差比PID控制器最大誤差減小了62.3%， 調定時間減少了26.96%； 從正弦跟蹤能力來看， 相較于PID 控制器，雙液壓缸滯后性明顯降低。 從以上分析對比可以看出， 反步法控制器能夠滿足雙缸同步控制要求。