中學數列的數學思想及其教學啟示

歐慧謀，黃紅梅，曹廣福

中學數列的數學思想及其教學啟示

歐慧謀1，2，黃紅梅1，曹廣福1

（1．廣州大學 數學與信息科學學院，廣東 廣州 510006；2．韓山師范學院 數學與統計學院，廣東 潮州 521041）

數學思想對學生的數學學習與未來發展具有深遠影響．數學教學應在強調知識的同時，充分挖掘蘊藏在知識背后的數學思想，并在教學中通過針對性問題促使學生領會．中學數列的數學思想包括函數思想、遞歸思想、由特殊到一般、數學歸納法、消項求和思想以及極限思想等方面．基于中學數列的數學思想，提出如下教學啟示：問題驅動概念教學，促進數列概念本質理解；從函數的角度審視數列，揭示兩者的內在關系；重視遞推公式教學，培養遞歸思維與發現能力；強化數學歸納法，拓展數學論證能力；誘發數列求和“好念頭”，滲透消項求和思想．

數列；數學思想；教學啟示

1 研究背景

什么是教育？愛因斯坦認為：“把在學校里學到的所有東西全部忘光之后留下來的東西才叫教育．”他的意思是，教育的核心價值并非知識的傳授，而在于思想與方法的領悟以及觀念與能力的提升．愛因斯坦的觀點在數學教育領域有極大的共鳴，R·柯朗在批評過分強調數學公理化風氣時曾指出：“創造發明的要素以及起指導和推進作用的直觀要素，雖然常常不能用簡單的公式來表述，但是它們卻是任何數學成就的核心．”[1]米山國藏則認為：“作為知識的數學出校門不到兩年就忘了，唯有深深銘記在頭腦中的數學精神、數學思想、研究方法和著眼點等，這些會隨時隨地發生作用，使人終身受益．”[2]中國學者鄭毓信持類似觀點，認為：“數學教學應當努力提升學生的思維品質，由理性思維逐步培養學生的理性精神．”[3]這些觀點無不說明，數學教學不能一味地追求數學知識，而應在強調數學知識的同時，促使學生獲得相應的、對未來數學學習與自我發展影響深遠的數學思想．

作為數學的重要概念，數列在現代數學的發展過程中發揮了重要作用．它既是數的拓展，又與函數關聯；既是極限的載體，又是級數的基礎；既在微積分中具有舉足輕重的作用，又對實分析與泛函分析產生了深遠的影響．弗賴登塔爾曾言：“無論從歷史的、發生的還是從系統的角度看，數的序列都是數學的基石，沒有數的序列就沒有數學．”[4]數列“基石”的意義不僅體現在知識層面，還應包括蘊含在知識背后的數學思想．中學數列主要涉及等差數列與等比數列兩類重要數列，內容雖然不多，但它們及其蘊含的數學思想，卻是研究一般數列、級數以及大學相關數學知識的基礎，也是進一步提升學生數學核心素養的重要載體．因此，教師不僅要關注數列知識，更要深刻認識數列的數學思想，這樣才能批判性地分析教材，合理設計教學．

2 中學數列內容的編排特點

《普通高中數學課程標準（2017年版2020年修訂）》（簡稱《課標》）將數列內容安排在選擇性必修課程“函數主題”部分．《課標》要求[5]，教學應幫助學生通過對日常生活中實際問題的分析，了解數列的概念；探索并掌握等差數列和等比數列的變化規律，建立通項公式和前項和公式；能運用等差數列、等比數列解決簡單的實際問題和數學問題，感受數學模型的現實意義與應用；了解等差數列與一元一次函數、等比數列與指數函數的聯系，感受數列與函數的共性與差異，體會數學的整體性．至于數學歸納法，《課標》則降低要求，僅把其列為選學不考內容．

各個版本教材根據《課標》要求編寫，體現較大共性，這里僅以人教版為例分析[6]．在內容安排上，教材首先介紹數列的概念及其表示方法，接著把重點放在等差數列與等比數列，最后介紹數學歸納法，體現由特殊到一般、循序漸進、主次分明的編排特點．在情境創設上，教材在概念的學習中創設了豐富的生活實例，包括年齡身高、月亮可見數、天壇石板、衣服尺碼、海拔氣溫、細胞分裂、銀行貸款等，這為學生認識數列提供了良好的條件．在邏輯推導上，非特殊數列（即非等差數列或者等比數列）的通項公式與遞推公式主要由特殊到一般地觀察發現，而特殊數列（即等差數列與等比數列）的通項公式與求和公式則通過推導得到．特別地，教材尤其注重從函數角度認識數列，不僅從離散函數的角度介紹數列，甚至通過解析式（即通項公式）、列表以及圖象等方式表征數列；在等差數列與等比數列章節，教材還分別詳細介紹了各自通項公式與一次函數、指數函數的關系．數學歸納法則作為證明數列命題的工具被引入，安排在數列最后一節．

顯然，《課標》作為教學指導性文件，側重數列知識的目標要求與教學指導，沒有明確提出數列知識蘊含哪些數學思想，更沒有告訴教師教學中如何滲透這些思想．而教材出于知識系統性、嚴謹性以及簡潔性的考量，同樣沒有告知數學思想．例如教材在推導數列通項公式時，盡管遵循“由特殊到一般”的發現路徑，但教材對此沒有明說；類似地，教材雖然介紹了遞推公式，但僅是蜻蜓點水，學生難以體會蘊含其中的遞推思想．《課標》與教材的分析無不說明，與顯性的數列知識相比，數列蘊含的數學思想具有隱性特征．這意味著，教師在備課與教學過程中，不應局限于《課標》，更不應把教材奉為“圣書”，而要深入數列知識的本質與來龍去脈，精準挖掘相關的數學思想，并在教學中加以滲透，這是實現真正數學教育的條件．

3 中學數列蘊含的數學思想

在梳理數列發展歷史的基礎上，綜合分析數列概念、遞歸特點、通項推導、求和思維、變化趨勢以及這些因素的內在邏輯關系，歸納出如下6個數列數學思想：函數思想、遞歸思想、由特殊到一般、數學歸納法、消項求和思想以及極限思想．

3.1 函數思想

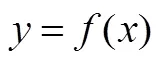
3.2 遞歸思想

遞歸思想指在某個推導過程中，后續的每一步都需要前一步或前幾步的信息與結果，這是一個從初始值開始，按照某種規律推導任意項的基本方法．遞歸思想并不遙遠，項武義曾指出：“自然數系的本質就是一個按順序排列的體系，起始者為1，往后每個數比其前一個數多加1，如此逐個加1以至于無窮；自然數系的加、乘和乘方運算都是由最原始的‘+1’運算逐步復合得到的．”[8]

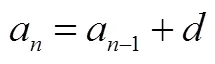
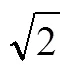
3.3 由特殊到一般

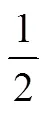
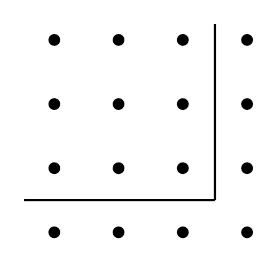
圖1 正方形數

伽利略曾在長期觀察行星運行的基礎上，依靠天文數據近似得到橢圓運動定律．牛頓與萊布尼茲所創立的微積分則是前人關于切線、最值、速度以及面積等具體問題的一般化結果．凸多面體的歐拉定理、費馬大定理、哥德巴赫猜想等同樣源于對特殊情況的考察．正如拉普拉斯所言：“即使在數學里，發現真理的主要工具也是歸納和類比．”由特殊到一般甚至可以延伸到日常生活，所謂經驗無非是在多次實踐后的反思性認識．從這個角度看，由特殊到一般的思維方法是每個人必備的基本素養．

3.4 數學歸納法

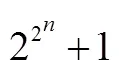
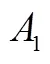
數學歸納法從其誕生起就與數列命題結下不解之緣．前述“正方形數”的研究可看成數學歸納法思想的源泉，但其本質上屬于不完全歸納，缺乏嚴謹性．1575年，莫羅利科巧妙利用遞推關系證明“正方形數”，即

并總結出證明類似命題的步驟．因這種方法與通常的歸納程序相似，且主要用于證明數學命題，后來奧古斯塔斯·德摩根把其稱為數學歸納法．

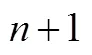
數學歸納法源于數列但超越數列，它在證明恒等式、不等式、數的整除、楊輝三角數、凸多邊形內角和公式、凸多面體歐拉定理等與正整數有關的命題時，發揮著無可代替的作用，因而是一種重要的數學論證方法．正如R·柯朗所言：“與亞里士多德的基本邏輯規則（即演繹推理‘三段論’）那樣，數學歸納法是數學的基本邏輯原則，每個學習數學的人，都應該掌握這種證明方法．”[1]這充分說明，新版教材增加數學歸納法是正確的．

3.5 消項求和

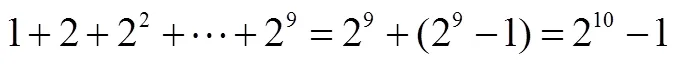
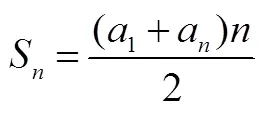
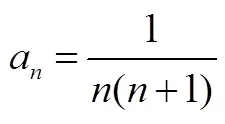
“消項求和”實際上是“降維思想”的一種具體形式，后者指把高維空間、高次方程、多元方程組、高維數據問題分別轉化為低維空間、低次方程、一元方程、低維數據問題從而解決問題的一種基本思想．“降維思想”在高維、多元、多變量等復雜問題中具有重要意義．以數據分析領域為例，人們經常要在不改變高維數據結構的前提下對數據作降維處理，以建構更具擴展性、通用性的數據模型．在數列教學中，教師應通過“消項求和”的學習促使學生進一步認識“降維思想”．

當然，數列求和的途徑并不是唯一的，還有其它途徑可循，“數形結合”就是其中之一．前述畢達哥拉斯學派利用“形數”求解數列之和就是其中代表，中國數學家沈括、楊輝、朱世杰同樣通過“垛積術”得到了諸如

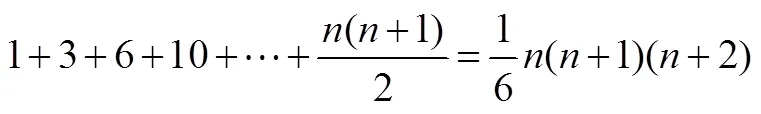
等數列求和公式[12]．因為“數形結合”不是中學數列求和的主流，這里暫且不做過多討論．

3.6 極限思想

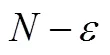
4 教學啟示

數學思想具有潛在的、隱性的特征，把這種潛在的、隱性的數學思想轉化為學生內在的個性素質還需要通過教與學活動來實現[14]．而問題是溝通數學知識與數學思想的橋梁，在數列教學中，教師應立足數列教學思想，設計針對性問題，激發學生數學思考，促使學生領會數學思想魅力．

4.1 問題驅動概念教學 促進數列概念本質理解

教材在引入數列、等差數列與等比數列概念時，雖然創設了豐富的生活實例，但缺乏具體的、指向性的問題．以數列的概念為例，教材提供了表1所示3個情境，但情境并沒有嵌入任何具體問題，而是給出各自數據的關鍵信息——按照確定順序排列，供學生分析學習，并通過問題“上述例子的共同特征是什么”引導學生抽象概括，得到數列的概念．從概念抽象的角度看，這種安排具有一定的合理性．但是，教材直接羅列與分析數據，替代了本可以由教師在課堂上引導學生進行的分析與思考，這將削弱培養學生數學思維能力的效率，不利于學生深度認識數列概念的函數本質．類似的情況同樣存在于等差數列與等比數列概念，例如教材雖然通過4個具體情境引入等差數列概念，卻沒有設計合適的問題引導讀者進一步思考其本質（等差遞推關系），而且某些數列有人為編造痕跡，缺少一定的真實性．

表1 數列概念學習情境

問題是數學概念與原理的源泉，應是數學概念與原理的教學起點．張奠宙認為：“問題驅動的本質是暴露數學的本質，把數學‘冰冷的美麗’轉化為‘火熱的思考’．教師在介紹基本概念、基本理論、基本定理時，不能滿足于形式地、演繹地給出，而要把數學本質用問題的形式揭露出來．”[15]在數列概念教學中，教師不妨結合數列歷史、本質以及學生經驗，尋找促使數列概念產生的本原性問題，以激發學生火熱的思考，促進數列概念本質的理解[16–17]．例如，在引入數列概念與等差數列概念時，教師可分別創設如下問題．

問題1 劉徽的割圓術是說用圓的內接正多邊形去逐步逼近圓，他從圓內接正六邊形出發，將邊數逐次加倍，邊數越多，正多邊形面積越接近圓面積．求半徑為的圓內接正6邊形的面積？當分別取1，2，3，…時，得到什么結論？

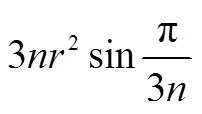
數學概念或原理的形成可以是源于現實生活、自然與工程或數學本身的問題，只要是具有啟發性、本原性、觸及數學本質、能夠在教學中起統帥作用的問題都是好問題、真問題[18]．既然學生在“數列的概念”一節已初步學習遞推公式，而它又是刻畫等差數列的工具，教師不妨在此基礎上創設數學情境，通過遞推公式引入等差數列．

當然，為豐富學生對數列概念的認識，教師可以在以上問題的基礎上，適當補充生活實例．

4.2 從函數的角度審視數列 揭示兩者的內在關系

教材通過解析式、圖象、表格等多元表征介紹了數列與函數、等差數列與一次函數以及等比數列與指數函數的內在關系，但缺乏深層次內在關系的探討，例題或者習題也甚少涉及函數思想．由此導致的可能結果是，學生盡管知道數列是一類特殊的函數，卻不清楚為什么要把數列看成函數，更不清楚尋找兩者關系的真正價值．事實上，連續函數離散化是從抽象到機械化實現的必經之路，數值計算的前提便是離散化．將數列看成特殊的函數以及在函數的定義域中取特殊的點從而形成一個數列（大多數情況下是根據節點數確定步長），進而將連續函數離散化以便機械化處理，此重要思想方法是人機對話得以實現的基礎．

從理論角度介紹數列與函數的內在關系是必要的，但理論有余、實踐缺乏的教學不利于學生深入認識二者關系．教師需要適時引導學生從函數的角度審視數列問題，尋找數列與函數之間的關系，進而借助函數模型的性質解決問題，體會函數思想在數列問題解決中的魅力．

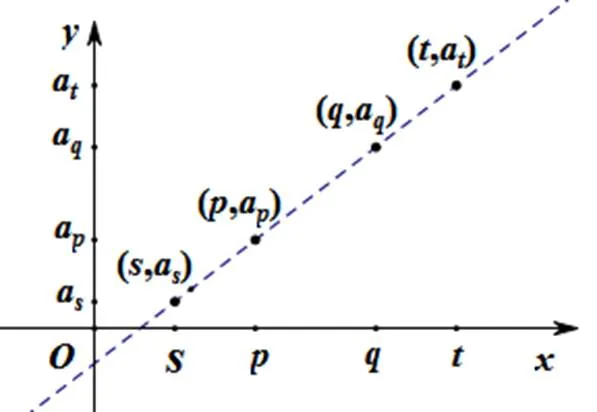
圖2 問題1函數圖象

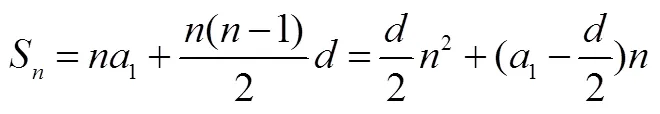
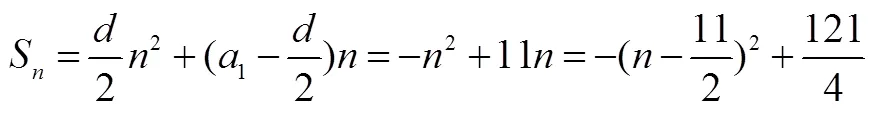
結合二次函數性質（如圖3所示），易可得的最大值為．

需要指出的是，教材從函數的角度介紹了數列的概念以及等差數列與等比數列的通項公式，但沒有明確等差數列與等比數列前項公式的函數屬性．數列求和是數列應用的焦點，數列和的最值、單調性等是人們經常需要解決的問題，這也是函數的重要問題，這些問題可以統一起來，利用函數的性質加以解決．因此，在介紹等差數列與等比數列前項公式時，教師不妨分別從二次函數與指數函數的角度加深認識．

4.3 重視遞推公式教學 培養遞歸思維與發現能力

但是，遞推公式是教學難點，教學很容易陷入復雜的細節與技巧的糾纏，導致學生產生恐懼心理．通項公式與遞推公式是表示數列的兩個重要工具，二者最大的不同在于，前者是數列的函數解析式，后者則是從遞推角度表示數列的模型．遞推公式本身具有很好的生活化情境認知基礎，教師給出遞推公式定義后，可以適當創設生活情境，豐富學生對遞推公式的認識，體會遞歸思想．由遞推公式推導通項公式時，宜引導學生學會由特殊到一般地發現規律，提升歸納與猜想的數學能力．

問題1 階梯形劇場第一排有20個座椅，后面每排比前排多1個座椅，劇場共有20排座椅，劇場各排座椅數構成的數列能否用遞推公式表示？

問題2 數學家斐波那契在觀察兔子繁殖時，提出一個有趣的問題：如果1對兔子每月生1對小兔子（一雄一雌），而每對小兔子在它出生后的第3個月里，又生1對小兔子，假定在不發生死亡的情況下，由1對初生的小兔子開始，50個月后會有多少對兔子？

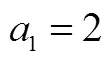
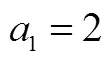
當然，依據遞推公式推導通項公式，除由特殊到一般途徑外，還有其它方法．例如，由斐波那契數列的遞推公式推導其通項公式的方法有多種，而適合中學生的初等方法是利用遞推關系構造一個新的等比數列[20]．

4.4 強化數學歸納法 拓展數學論證能力

數學歸納法屬于選修不考內容，但鑒于它的重要性，高中生學習數學歸納法是必要的．一方面，高中生無論是辯證思維還是知識儲備都有了長足的發展，完全有能力學好、用好數學歸納法．另一方面，介紹數學歸納法是國際數學課程的普遍要求[21]，新加坡H2數學考試（相當于中國理科高考數學）甚至經常考查學生利用數學歸納法證明數列命題的能力[22]．中國雖然對此沒有考試要求，但如果學生了解數學歸納法，在遇到數列等與正整數有關的問題時，至少可以減少直覺錯誤，甚至多一種求解選擇．

與其探討要不要介紹數學歸納法，不如探討怎么教授數學歸納法．教材在給出等差數列通項公式后，沒有直接證明公式，而是通過分析多米諾骨牌游戲類比介紹數學歸納法，最后才回頭利用數學歸納法進行證明．數學歸納法主要源于數學問題，而不是多米諾骨牌游戲，教材通過多米諾骨牌游戲直接介紹數學歸納法是否合理，有待商榷．弗賴登塔爾在批評數學歸納法教學時就曾指出：“學習數學歸納法的正確途徑是向學生提出一些必須用數學歸納法才能解決的問題，迫使學生直觀地使用這個方法，從而發現這個方法．”[4]依其觀點，通過數列問題介紹數學歸納法或許更合適．當然，這并非否定多米諾骨牌游戲的意義，事實上，給出數學歸納法定義后，教師有必要把其基本步驟與多米諾骨牌游戲進行類比．

問題2 數學歸納法可靠嗎？你能否類比多米諾骨牌游戲說一說其可靠性？

問題3 歸納推理與數學歸納法有何異同與關聯？

以上問題層層遞進，共同促進學生發現、認識、應用數學歸納法．其中，問題1可以促使學生在通項公式的證明中發現數學歸納法，同時揭示學習數學歸納法的緣由．問題2意在引導學生類比多米諾骨牌游戲，直觀認識數學歸納法，消除可靠性疑慮．問題3有助于啟發學生厘清歸納推理與數學歸納法的關系，凸顯數學歸納法的演繹推理屬性．另外，教材關于數學歸納法的應用僅限于數列命題，這容易使學生產生“數學歸納法只能證明與數列有關命題”的錯覺，問題4恰好可以彌補教材遺憾．

4.5 誘發數列求和“好念頭” 滲透消項求和思想

教材分別通過“倒序相加法”與“錯位相減法”推導等差數列與等比數列前項和公式，從純數學推導的角度看，學生對這些方法不存在認知上的困難，他們甚至對方法之巧妙贊嘆不已[24]．但這樣的方法是如何想到的？學生往往不明所以．在他們眼里，這些方法猶如從帽子里跳出來的兔子，突兀得讓人不知所以然．如果教師對此沒有足夠的思考與措施，教學容易糾纏于技巧與細節．波利亞認為，數學解題的關鍵在于誘發“好念頭”[25]．教師不妨從數列求和的矛盾與思想出發，誘發學生對數列求和產生“好念頭”．

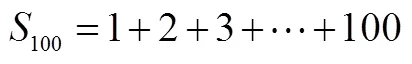
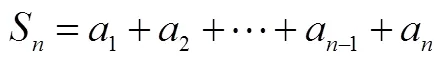
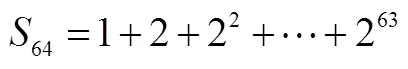
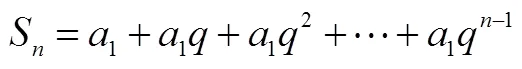
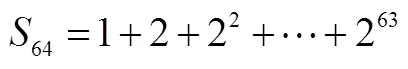
問題1 這是一個什么問題？怎么求解？

問題2 前面用什么方法推導等差數列的前項求和公式？它可以用來計算該問題嗎？

問題3 雖然“倒序相加法”無法直接計算該問題，但從中能否得到什么啟發？

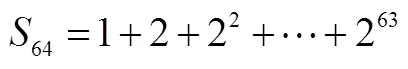
5 結束語

教育的全部目的就是使人具有活躍的智慧[26]．數學知識并非不重要，事實上它是學生發展必不可少的基礎．然而，停留在數學知識傳授的教學不是真正的數學教育，那種只灌輸數學知識、忽略數學思想的教學，既不利于學生理解數學的本質，也無法激發對數學火熱的思考，更無助于學生的自我發展．數學教學應揭示發現、建構數學知識的一般策略與方法，增強學生主動建構、創造數學知識的意識與能力，這樣才能使數學核心素養落到實處[27]．

但是，數學思想的隱性特征要求教師深入認識數學知識的本質與來龍去脈，精準挖掘數學知識背后的數學思想，這樣才能設計科學合理的教學方案，引導學生在數學知識的形成與發展過程中領會相關的數學思想．另一方面，學生對數學思想的領會是一個循序漸進的過程，不可能一蹴而就，教師需要通過不同數學知識的教學有意識地加以滲透．顯而易見，數學思想對學生數學學習與未來發展的影響是一個長期的、潛移默化的過程．

[1] R·柯朗，H·羅賓．什么是數學[M]．左平，張飴慈，譯．上海：復旦大學出版社，1995：3．

[2] 米山國藏．數學的精神、思想和方法[M]．毛正中，吳素華，譯．上海：華東師范大學出版社，2019：序1–2．

[3] 鄭毓信．數學思維教學的“兩階段理論”[J]．數學教育學報，2022，31（1）：1–6，78．

[4] 弗賴登塔爾．作為教育任務的數學[M]．陳昌平，唐瑞芬，譯．上海：上海教育出版社，1995：160．

[5] 中華人民共和國教育部．普通高中數學課程標準（2017年版2020年修訂）[M]．北京：人民教育出版社，2020：38．

[6] 人民教育出版社課程教材研究所．普通高中教科書·數學選擇性必修第二冊[M]．北京：人民教育出版社，2020：1–57．

[7] 莫里斯·克萊因．古今數學思想（第一冊）[M]．張理京，譯．上海：上海科學技術出版社，2014：308–309．

[8] 項武義．基礎代數學[M]．北京：人民教育出版社，2004：5–8．

[9] 李昌官．遞推：數列的靈魂[J]．數學通報，2018，57（10）：22–25．

[10] 胡國定．簡明數學詞典[M]．北京：科學出版社，2000：557．

[11] 涂榮豹．數學教學設計原理的建構——教學生學會思考[M]．北京：科學出版社，2018：130．

[12] 李文林．數學史概論[M]．3版．北京：高等教育出版社，2012：100–102．

[13] 卡茨．數學史通論[M]．李文林，譯．北京：高等教育出版社，2018：88–89．

[14] 王道俊．知識的教育價值及其實現方式問題初探——兼談對杜威教育思想的某些認識[J]．課程·教材·教法，2011，31（1）：14–32，43．

[15] 張奠宙，張蔭南．新概念：用問題驅動的數學教學[J]．高等數學研究，2004（3）：8–10．

[16] 曹廣福，張蜀青．論數學課堂教學與評價的核心要素——以高中導數概念課為例[J]．數學教育學報，2016，25（4）：17–20．

[17] 呂松濤，曹廣福．高中向量教學中數學思想的滲透[J]．數學教育學報，2021，30（4）：19–24．

[18] 王海青，曹廣福．問題驅動數學教學的基本原則與思想及其實施步驟[J]．數學教育學報，2022，31（1）：24–27．

[19] 李子瞻，胡典順．基于數學核心素養的新舊高考比較分析——以2021年新高考Ⅰ卷與2020年全國Ⅰ卷為例[J]．數學教育學報，2022，31（3）：26–31．

[20] 曹廣福，張蜀青，歐慧謀．問題驅動的中學數學課題教學（函數與微積分卷）[M]．北京：清華大學出版社，2022：35．

[21] 王科，汪曉勤．“中美日新”四國高中教材中的數學歸納法比較研究[J]．數學教育學報，2015，24（2）：40–45．

[22] Singapore ASIA Education. Past examination papers arranged by year 2011—2020: A level h2 mathematics yearly edition [M]. Singapore: Singapore Asia Publishers Pte Ltd, 2021: 不詳.

[23] 張雄，李得虎．數學方法論與解題研究[M]．2版．北京：高等教育出版社，2003：54．

[24] 張蜀青．數列教學中的數學思想之光[J]．數學通報，2021，60（2）：45–48．

[25] 涂榮豹．數學解題學習中的元認知[J]．數學教育學報，2002，11（4）：6–11．

[26] 懷海特．教育的目的[M]．徐汝舟，譯．北京：生活·讀書·新知三聯書店，2022：66．

[27] 李昌官．數學發現與發明關系新說[J]．數學教育學報，2022，31（1）：97–102．

The Mathematical Thoughts of Number of Sequence in Middle School and Its Teaching Enlightenment

OU Hui-mou1, 2, HUANG Hong-mei1, CAO Guang-fu1

(1. School of Mathematics and Information Science, Guangzhou University, Guangdong Guangzhou 510006, China;2. School of Mathematics and Statistics, Hanshan Normal University, Guangdong Chaozhou 521041, China)

Mathematical thoughts have a profound impact on students’ mathematical learning and future development. Mathematics teaching should not only emphasize knowledge, but also fully excavate the mathematical thoughts behind knowledge, and promote students’ understanding through targeted questions during teaching. The mathematical thoughts of number of sequence in middle school include function thought, recursion thought, from special to general, mathematical induction, elimination and summation thought, limit thought, etc. Based on the mathematical thoughts, the following teaching implications of number of sequence are proposed:problem-driven concept teaching promotes understanding of the essence of sequence concept; examines the sequence of numbers from the perspective of function to reveal the internal relationship between them; pays attention to the teaching of recursive formulas to cultivate recursive thinking and discovery abilities; emphasize mathematical induction to expand mathematical argumentation capabilities; and induces the good idea of summation of the sequence to infiltrate the elimination and summation thought.

sequence of number; mathematical thoughts; teaching enlightenment

G632.0

A

1004–9894（2024）01–0001–07

歐慧謀，黃紅梅，曹廣福．中學數列的數學思想及其教學啟示[J]．數學教育學報，2024，33（1）：1-7．

2023–10–02

國家“萬人計劃”人才項目——問題驅動的數學課堂教學理論與實踐；“粵港澳大亞灣國家應用數學中心”項目——問題驅動的中小學數學教育研究（2020B1515310020）；韓山師范學院教育教學改革項目——問題驅動視角下的數學教學研究（0006/E22110）

歐慧謀（1982—），男，廣西玉林人，講師，博士生，主要從事數學課程與教學論研究．曹廣福為本文通訊作者．

[責任編校：周學智、陳漢君]