山地城市互通式立體交叉同側相鄰匝道最小凈距計算研究

楊進, 龔華鳳,2, 趙聰霄,2

(1.林同棪國際工程咨詢(中國)有限公司, 重慶 401121; 2.重慶市山地城市可持續交通工程技術研究中心, 重慶 401121)

互通式立交作為城市交通系統中的重要交通節點,起著車流轉換和道路之間連接的作用。隨著道路里程和路網密度的增加及立交建設的復雜化,立交主線出現連續匝道出入口的情況越來越多。

相比于平原城市,山地城市地形高低起伏,道路縱坡大,除高速路與快速路外,在城市主、次干道上存在大量互通立交。該類互通立交的主線設計速度偏低,交通流量大,立交功能多樣,為滿足轉換需求,相鄰匝道間易形成短距離的連續匯入、匯出。作為山地城市路網規劃和立交布局的重要研究內容,連續合、分流點凈距直接影響立交的選型、規模、投資等,也影響互通式立交車輛運行狀態。匝道連續分流點凈距過大,則無法滿足交通轉換需求;匝道連續分流點凈距過小,則會影響互通立交的通行能力和交通安全水平。

1 研究現狀

美國等西方國家對互通式立交匝道間距與交織段的研究較早且成果較多,但因交通系統的復雜性,無法達成統一認知。1950年發布的《公路通行能力手冊》(HCM 1950)基于多個州的實測數據,首次提出了針對公路交織區運行與設計的分析方法[1]。1965年發布的HCM 1965根據Normann O. K.、Karl Moskowitz等的研究成果,進一步區分了不同服務水平下進出匝道與主線的交織分析,擴大了交織段長度與交織流量的選擇設計范圍,但未明確交織段和上下游服務水平的影響[2]。Denney R. W.等考慮不同交織構型對交織段的影響,將交織段進一步分為主線交織和匝道交織,認為交織車輛與非交織車輛在同一服務水平下的運行速度不同[3]。文獻[4]對交織區通行能力進行修改并形成了新的計算方法,但由于計算過程煩瑣,該方法未得到廣泛應用。1985年發布的HCM 1985對匝道端部通行能力分析方法進行修訂,并考慮了匝道變速車道長度對主線外側兩條車道交通流分布的影響[5]。2010年發布的HCM 2010對交織長度、寬度和構型等進行了全新定義,同時更新了交織區通行能力計算方法[6], 但計算僅針對高速公路環境,計算中無法考慮低速下交織段通行能力。Leisch J. E.等根據大量實測交通數據,通過統計學方法和數理學方法,得出了不同交織構型情況下服務水平、交織流量、交織密度及高峰小時系數等與車道數之間的關系[7],該方法被納入美國加利福尼亞州《公路設計手冊》(HDM)[8]并沿用至今。

國內目前對互通立交凈距的研究成果和設計標準多基于公路項目。賀玉龍等從駕駛員心理特征入手,建立了城市快速路互通立交最小間距計算模型[9],但預測結果基于最不利駕駛情況且假設較保守,導致預測間距過大。吳明先等分析了八車道高速公路小間距互通式立交間車輛的運行特性和變道行為,構建了最小凈距計算模型,并運用數理方法結合調查數據標定了八車道高速公路小間距互通式立交最小凈距模型的關鍵參數[10]。孫劍等對上海市60處快速路典型交織區進行調查,通過分析典型因素與交織區通行能力之間的關系,提出了城市快速路交織區通行能力模型[11]。徐俊軍通過交通仿真軟件模擬快速路出入口的交通運行狀況,以主路車道數、主路流量、出入口交織比等影響快速路出入口間距的因素作為外部條件,對不同建設條件下快速路出入口最小間距進行了細化,預測結果與實際結果擬合較好[12]。

現行設計標準、規范對匝道凈距的概念及范圍尚未形成統一,導致不同標準、規范的要求差異較大。JTG/T D21—2014《公路立體交叉設計細則》中,相鄰互通立交最小凈距根據主線設計速度和主線車道數確定,但未提供建議值的計算過程[13];CJJ 129—2009《城市快速路設計規程》對快速路上相鄰出入口間距(端部之間的距離)最小值的規定見表1[14];CJJ 152—2010《城市道路交叉口設計規程》根據不同相鄰匝道組合形式(見圖1)提出了相鄰匝道出入口凈距的一般值和極限值(見表2)[15]。

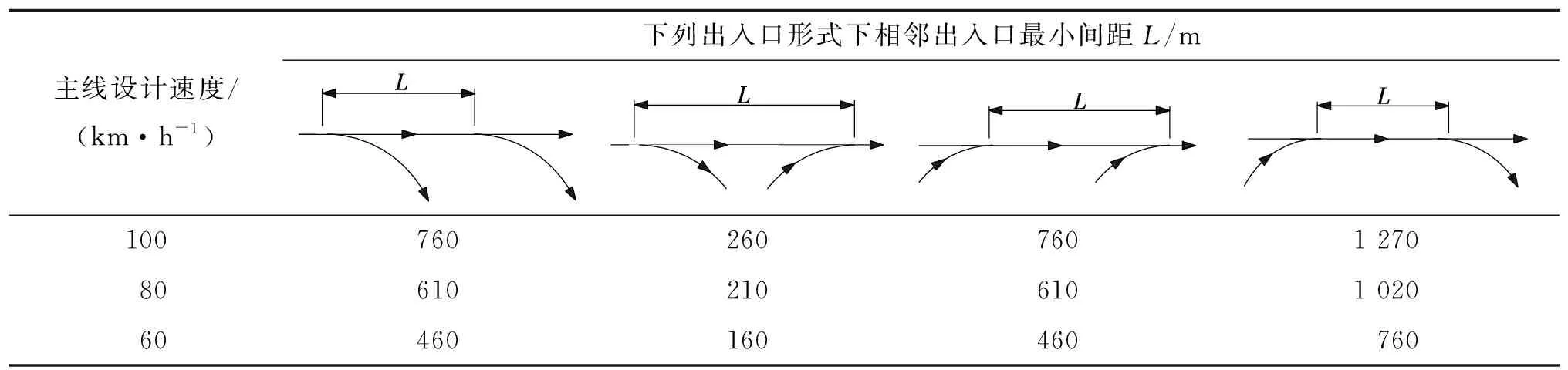
表1 CJJ 129—2009中相鄰出入口的最小間距L

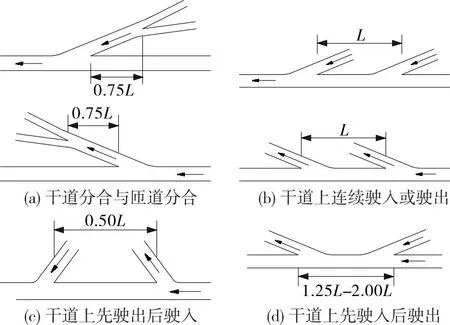
圖1 相鄰匝道組合形式

1.1 最小凈距的定義

最初對相鄰匝道距離L的界定源于美國的一系列研究成果。早期統一稱為匝道距離,后期逐漸對匝道細部進行了明確。AASHTO綠皮書(2004版)將相鄰匝道距離定義為相鄰匝道鼻端而非物理楔形端點之間的距離[16]。得克薩斯州《道路設計手冊》中建議值也指鼻端之間的距離[17]。

《公路立體交叉設計細則》定義立交相鄰匝道凈距為相鄰入、出口之間主線基本路段的最小長度,包括變速車道漸變段,但不包括變速車道長度。《城市快速路設計規程》明確相鄰出入口端部之間的距離為匝道間距,包含加減速車道長度。《城市道路交叉口設計規程》中未明確相鄰匝道凈距定義,但指出匝道出入口之間的間距應考慮變速車道長度,即凈距不包含加減速車道長度。

綜上,將匝道最小凈距定義為相鄰入、出口之間主線基本路段的最小長度(見圖2)。

圖2 相鄰立交匝道最小凈距示意圖

1.2 交織段長度的定義

根據Leisch J. E.的研究成果和HCM 2000,交織段長度指交織區入口處三角端寬度0.6 m 位置到出口處三角端寬度3.7 m 處的距離。后期研究中對交織段長度的定義出現爭議,HCM和美國得克薩斯州《道路設計手冊》[17]中共包含3種長度:1) 最短交織段長度LS,指相鄰入、出口之間主線基本路段的最小長度;2) 基本交織段長度LB,指相鄰匝道物理楔形端點之間的距離;3) 最長交織段長度LL,指相鄰匝道鼻端之間的距離。3種交織段長度見圖3。美國加利福尼亞州《公路設計手冊》(HDM)將交織段長度定義為相鄰匝道物理楔形端點之間的距離[8]。

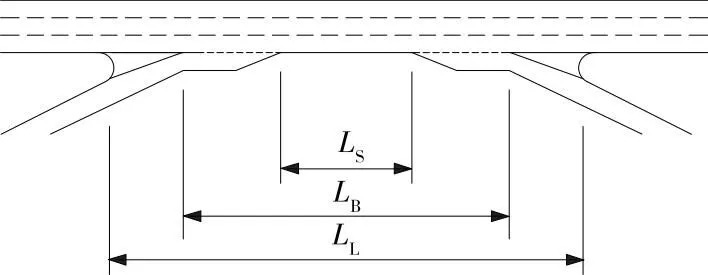
圖3 不同交織段長度定義示意圖

國內研究普遍認為交織段長度=減速車道長度+加速車道長度+漸變段長度×2+輔助車道長度[18-19]。

綜上,基于交織段為車輛完成車道變換提供空間的作用,經過對比國內外標準、規范的要求及相關研究成果,將同側先駛入、后駛出匝道之間合理的交織段長度定義為相鄰匝道凈距+漸變段長度×2,即相鄰匝道物理楔形端點之間的距離(LB)。

2 匝道凈距計算模型

HDM中使用Leisch法,通過圖表的形式考慮匝道構型(同側或雙側)和車道數配置(平衡或不平衡)進行交織段參數選擇,不同服務水平下可通過交織段流量確定交織長度建議值,具體關系見圖4。

1英尺≈ 0.305 m

2.1 確定服務水平

美國標準評價方法中將連續流條件下道路服務水平分為A～F 6個等級,CJJ 152—2010《城市道路交叉口設計規程》將道路服務水平分為一、二、三、四 4個等級,其對應關系見表 3。考慮到城市立交多為B類(一般立交),對立交主線與一般服務水平的匝道均建議采用Ⅱ2級服務水平(相當于美國標準中D級)下相關折減系數,針對D級服務水平(LOS D)計算對應交織段長度。

表3 中美標準、規范中立交服務水平的對應關系

2.2 確定交織段流量

HCM中將需要進行變換車道的交通量視為交織交通量。當車輛由匝道進入主路或離開主路進入匝道時,均需要進行車道變換。因此,可假設最大交織流量產生于所有入口匝道車輛都將匯入主線且出口匝道達到最大流量時。最大交織段流量為進匝道最大流量VRM和出匝道最大流量VMR之和。

按照不同匝道的交織構型(匝道車道數配置),匝道最大通行量可根據匝道基本路段通行能力C在不同立交服務水平下的比例αR進行折減。同時交織段因匝道和主線車輛有交織沖突,還應考慮主線在相對應服務水平下的折減αM。綜上,交織段流量計算公式為:

式中:N=進匝道車道數+出匝道車道數

匝道通行能力見表 4,Ⅱ2級服務水平下折減比例見表 5。

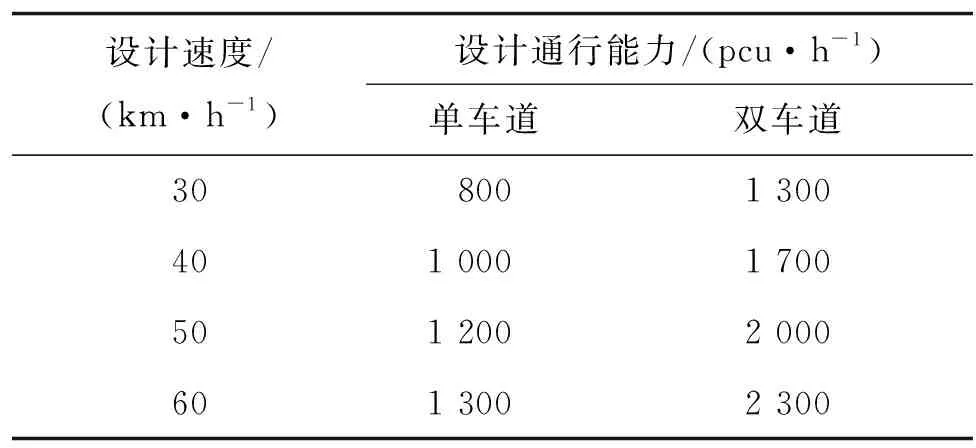
表4 匝道基本路段的設計通行能力

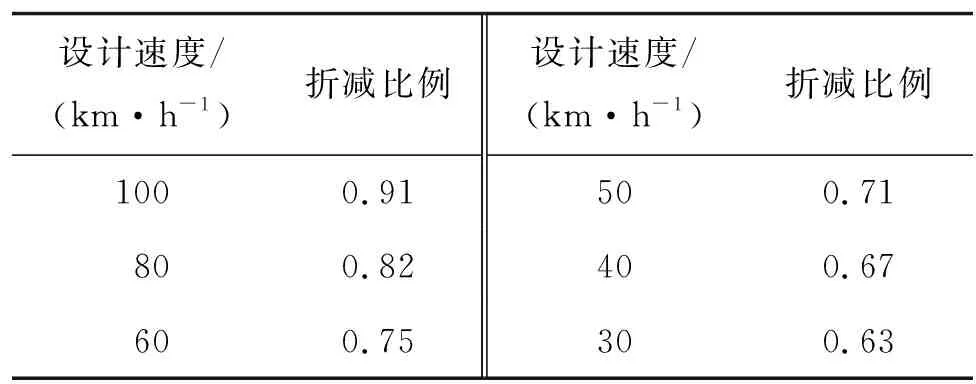
表5 Ⅱ2級服務水平下最大通行量折減比例V/C(CJJ 152—2010)

先根據D級服務水平下不同主線和匝道構型的最大交通量,計算得到預測交織流量Vw,然后根據HDM設計曲線得到交織段長度,最后根據CJJ 129—2010要求確定相鄰匝道入、出口兩端的漸變段長度,從而得到凈距長度計算值。

3 同側相鄰入、出口匝道最小凈距建議值比較

將HDM相鄰匝道最小凈距與JTG/T D21—2014、CJJ 129—2009、CJJ 152—2010及英國設計標準DMRB[20]、國內相關研究成果[12]中相鄰入口、出口匝道形式下最小凈距建議值進行比較。為了便于在同一維度進行比較,根據工程項目建設經驗,對標準中建議值做如下假設:1) JTG/T D21—2014對不同匝道速度和匝道數未作要求,但最小凈距隨著主線車道數的增加而增加,根據一般山地城市主線車道數,采用主線單向三車道情況下的凈距建議值。2) CJJ 152—2010規定在先駛入、后駛出的情況下最小凈距L所乘系數為1.25L～2.00L,根據不同匝道速度對系數進行選擇,假設60 km/h時采用2.00L、50 km/h時采用1.75L、40 km/h時采用1.50L、30 km/h時采用1.25L。3) CJJ 129—2009假設出入口最小凈距=最小間距-兩側匝道加減速過渡段長度。根據以上計算和假設,結合凈距與交織段的關系,對不同標準、規范及相關研究中最小凈距建議值進行比較,結果見表 6、圖5。

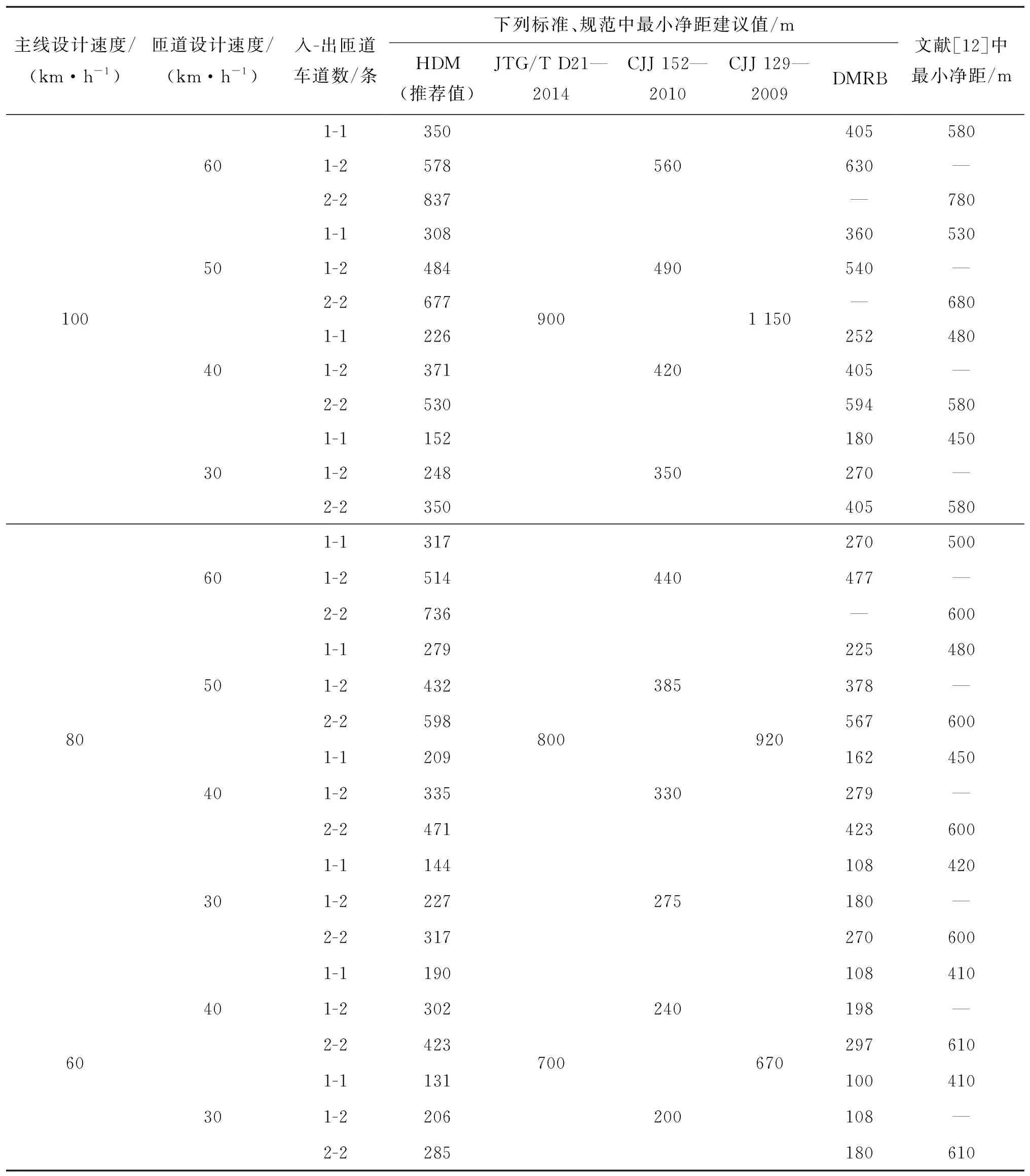
表6 不同標準、規范及相關研究中最小凈距建議值比較

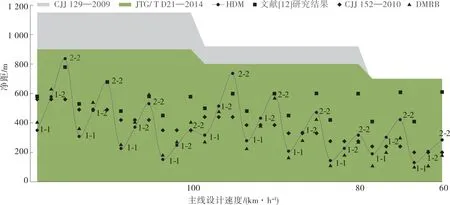
圖5 不同標準、規范與研究成果中最小凈距比較

從表 6、圖5可以看出:1) 在30種不同工況(不同入-出匝道車道數)下,CJJ 129—2009的最小凈距長度建議值均高于推薦值,平均偏差為61%。CJJ 129—2009未考慮不同匝道組合情況下交織流量對最小凈距的影響,其建議值僅與主線速度相關且最小凈距過長,在城市立交環境中可能較難實施。2) JTG/T D21—2014的最小凈距建議值均高于推薦值,平均偏差為55%。JTG/T D21—2014僅考慮不同主線車道數對交織段長度的影響,忽略了交織段長度即交織流量與匝道通行能力的直接關系,考慮到公路對速度和密度的要求更高,JTG/T D21—2014最小凈距建議值不適用于集約型城市立交。3) CJJ 152—2010的最小凈距建議值中50%大于推薦值,平均偏差為30%。這是由于CJJ 152—2010建議值僅考慮交織流量低(匝道≤二進一出)情況下的最小距離,雙進雙出情況則通過增加輔助車道另行設計。此外,CJJ 152—2010建議值是基于駕駛員辨認標志所需時間5～10 s確定的最小距離,未考慮車輛在交織段中的運行特征,在流量較大的情況下其取值偏小。4) 英國設計標準DMRB的最小凈距建議值中10%大于推薦值,平均偏差為25%。DMRB采用與HDM類似的系統,在不同主線密度和設計速度下考慮交織流量對最小凈距的影響。5) 文獻[12]的最小凈距建議值中53%大于推薦值,平均偏差為38%。文獻[12]通過建立VISSIM仿真模型,考慮交織過程中車輛組成、主線交通量、運行速度和優先通行權等因素的影響確定城市快速路出入口間距,由于模型中交通量和V/C比選擇范圍有限,未能給出交織流量較大情況下的最小凈距。

4 結論

本文針對中國規范對城市立交相鄰匝道凈距定義不明確、設置不合理的問題,通過對比國內外研究體系明確最小凈距和交織段的定義和構成,并基于美國加利福尼亞州《公路設計手冊》(HDM),考慮主線速度、匝道速度、車道數、組合形式、服務水平等因素,計算同側先入后出相鄰匝道間的最小交織長度推薦值。將該推薦值與JTG/T D21—2014、CJJ 129—2009、CJJ 152—2010及英國設計標準DMRB、文獻[12]中凈距建議值進行對比,推薦值介于上限值(JTG/T D21—2014與CJJ 129—2009)和下限值(CJJ 152—2010和文獻[12])之間,與 DMRB建議值的擬合度較高。

山地城市存在立交多、立交形式復雜且交通流量大等特點。根據工程項目建設經驗,山地立交相鄰匝道凈距如直接采用JTG/T D21—2014與CJJ 129—2009建議值則過于保守,而直接采用CJJ 152—2010建議值會導致凈距過小。HDM模型經過美國加利福尼亞州多個山地城市立交實踐證明其取值合理,同時該模型采用圖表查閱,簡單直觀,適用于山地城市新建、改建立交匝道的設計與評價。