結構參數變化對大跨度斜拉橋動力特性的影響分析

李云逸

(長沙理工大學 土木工程學院, 湖南 長沙 410114)

結構動力特性是結構本身的固有特性,它取決于結構剛度、質量、質量分布及支撐條件等[1]。斜拉橋的抗風性能、抗震性能及結構體系問題都與動力特性密切相關,因此對斜拉橋進行動力特性分析十分必要。針對大跨度斜拉橋動力特性的影響因素分析,Ni Y. Q.等采用SVM技術將溫度效應對汀九斜拉橋振動頻率的影響進行了量化[2];張志恒等以某大跨度雙塔雙索面斜拉橋為例,在對拉索彈性模量進行修正的前提下,分析了主梁剛度、主塔剛度及斜拉索截面積變化對斜拉橋動力特性的影響[3];吳興邦等分析了加勁梁彈性模量、橫向抗風支座及邊跨輔助墩等參數對三塔斜拉橋動力特性的影響[4];趙瀚瑋等基于黃岡公鐵兩用斜拉橋結構振動加速度與結構溫度的長期監測數據,研究了溫度對橋梁豎向動力特性的影響[5];楊志魁研究了自質量、剛度、有無縱向水平索、索力大小對西安富裕路灃河鋼拱塔斜拉橋動力特性的影響[6]。上述文獻主要對寬度較小的斜拉橋動力特性影響因素進行分析,對大跨度寬幅斜拉橋的研究較少。本文以武漢西四環漢江特大橋為研究對象,采用ANSYS有限元軟件建立斜拉橋有限元模型,分析二期恒載、拉索損傷和拉索斷裂等結構因素對大跨度斜拉橋動力特性的影響。

1 工程概況

武漢西四環漢江特大橋主橋為寬幅雙塔雙索面半漂浮體系混凝土斜拉橋,長度714 m,主跨分布為77 m+100 m+360 m+100 m+77 m,橋面寬度44 m。主梁為雙邊箱Π形梁,主塔為H形,每個索面有28對斜拉索。主要構件的材料參數見表1、表2,拉索編號規則見圖 1。

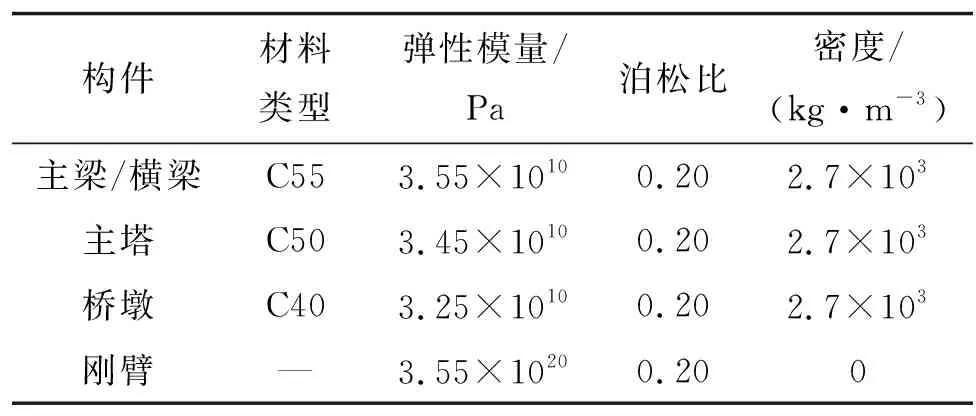
表1 斜拉橋主要構件的材料參數

2 斜拉橋有限元分析模型

為確保橋梁模型動力分析的準確性,在建立有限元模型時,結構質量、剛度及邊界條件的設置應與工程實際相符[7]。采用ANSYS有限元軟件建立漢江特大橋脊骨梁式空間桿系模型,主梁、剛臂(塔柱和塔柱間橫梁)和橋墩、橋塔均采用Beam 188單元模擬,拉索采用Link 10單元模擬,對主塔進行變截面處理。全橋共劃分為1 105個單元。全橋有限元模型見圖2。

表2 拉索的材料參數

圖1 漢江特大橋拉索編號示意圖

圖2 漢江特大橋有限元模型

該橋為半漂浮體系,主梁、主塔固結,橋墩、橋塔底部固結,主梁、橋墩施加橫向和豎向約束,對主梁、主塔處作耦合處理。

3 結構動力特性分析

漢江特大橋前20階振動頻率、振型見表3。根據表3,漢江特大橋的基頻為0.395 75 Hz,不屬于長周期(不超過5 s),對應振型為主梁和主纜的一階對稱豎彎;各階頻率差值較小,頻率出現集聚現象,與大跨度半漂浮體系斜拉橋動力特性的一般規律相符;主塔第3～6階模態出現橫彎,高聳空心塔柱的抗彎剛度較弱。

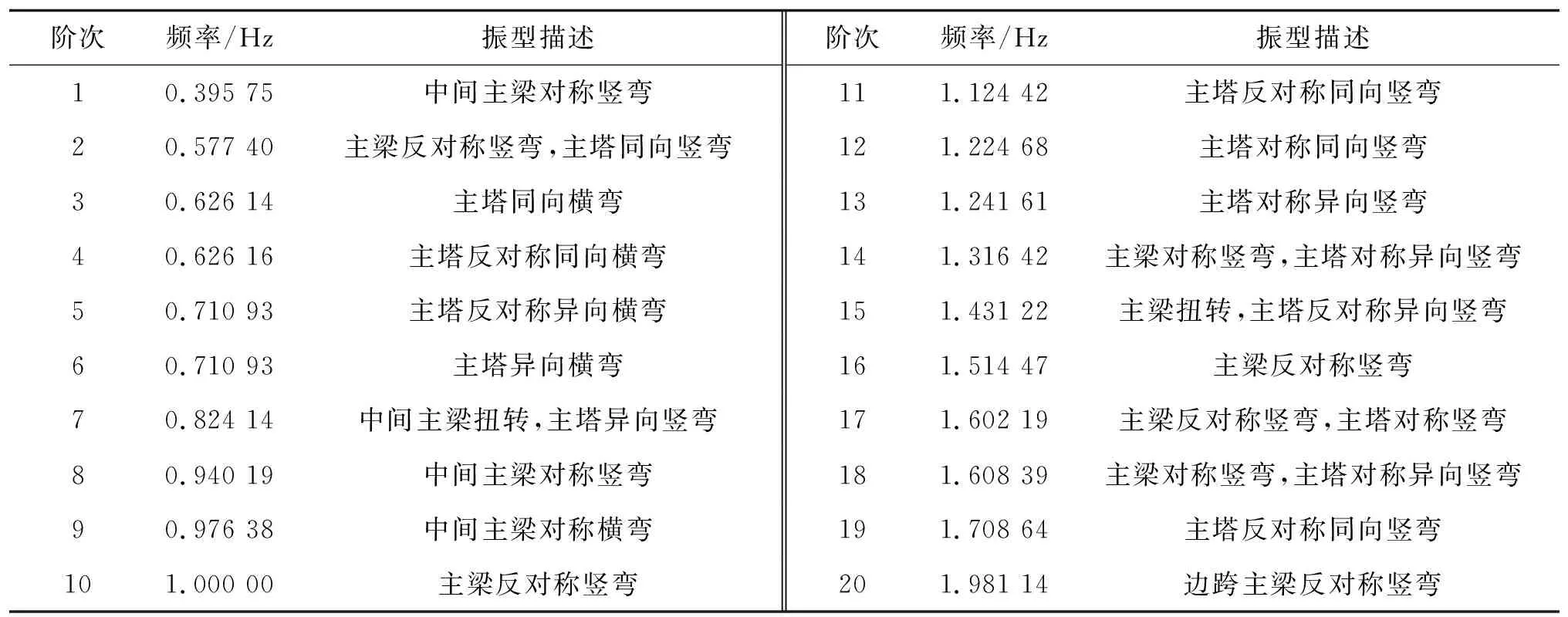
表3 漢江特大橋前20階自振頻率和振型描述

4 結構參數變化對動力特性的影響

斜拉橋自振頻率會受到斜拉橋結構質量和剛度的影響[1],橋面更換、斜拉橋二期恒載會因此產生變化。相關研究表明,二期恒載盡管在恒載質量中占比不大,但不可忽略,會改變大跨度斜拉橋的自振頻率[8];拉索損傷對橋梁動力性能存在影響[9-10],拉索受到損傷后其有效面積減小,彈性模量折減,拉索損傷程度越大,對動力特性的影響越大[11];拉索斷裂后斜拉橋結構內力重分布,會增大結構倒塌的風險,正確評估拉索斷裂情況下斜拉橋的動力性能是斜拉橋抗倒塌研究的重要內容[12]。結合漢江特大橋的實際情況,對不同二期恒載、拉索彈性模量及拉索斷裂時該橋的動力特性進行計算,分析結構參數變化對該橋動力特性的影響。

4.1 二期恒載變化對動力特性的影響

根據該橋可能維修的情況,將二期恒載分別降低和提高10%、20%進行動力特性計算,分析二期恒載變化對該橋動力特性的影響。不同二期恒載下該橋前10階振動頻率見表4。

由表4可知:正負20%以內二期恒載變化對該橋動力特性的影響較小,各階振動頻率變化率均小于0.1%;增大二期恒載,自振頻率降低;減小二期恒載,自振頻率增大。

表4 不同二期恒載下斜拉橋的振動頻率

4.2 拉索損傷對動力特性的影響

隨著橋梁服役時間的增長,拉索會出現損傷。拉索損傷主要包含拉索承載截面積減小和材料性能劣化引起拉索彈性模量改變兩方面[13-14]。拉索彈性模量變化是拉索剛度改變的可能因素之一。拉索未損傷時的彈性模量為1.95×1011Pa,考慮拉索性能劣化導致彈性模量分別減小5%和10%、拉索銹蝕等導致拉索有效截面積分別減小5%和10% 4種工況,分析拉索損傷對該橋動力特性的影響。各工況下該橋前20階振動頻率見表5。

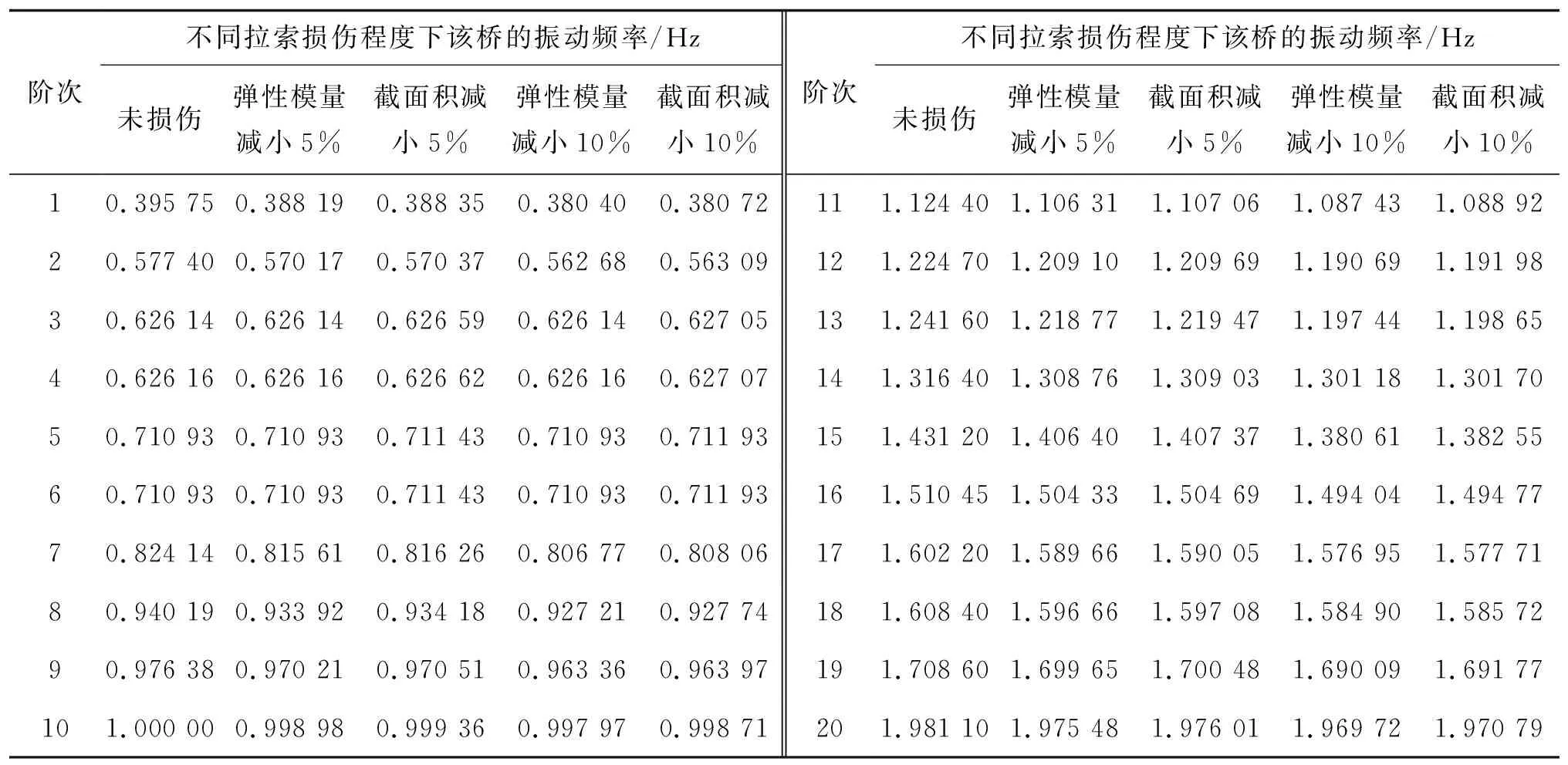
表5 拉索損傷對斜拉橋動力特性的影響

由表5可知:隨著拉索損傷程度的增大,該橋振動頻率減小,且振動頻率變化率增大,對橋梁動力特性的影響增大。拉索損傷對該橋第3～6階及第10階振動頻率幾乎沒有影響;對第7～9階、第14階及第17～20階振動頻率有影響,但改變率小于2.00%;對第1～2階、第11～13階及第15～16階振動頻率的影響較顯著,最大改變率約為3.95%。另外,拉索承載截面積變化對該橋動力特性的影響略大于彈性模量變化的影響。

4.3 拉索斷裂對動力特性的影響

斜拉橋按超靜定結構設計,通常可以經受某根拉索的斷裂,但各索力的重新分配會加速拉索的疲勞損傷甚至導致拉索發生斷裂。在該橋上游端選取9×4=36根拉索模擬拉索斷裂。根據相關研究成果,長索斷裂對斜拉橋動力特性的影響較明顯。因此,在長索區設置更多的拉索斷裂工況,每跨均勻選取9種拉索斷裂工況進行研究。不同拉索斷裂工況下該橋的動力特性變化見圖3～6。

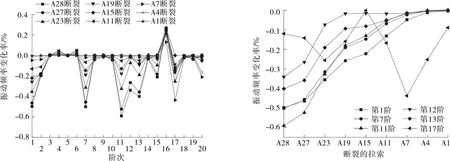
圖3 3#塔邊跨單根拉索斷裂工況下斜拉橋的振動頻率變化

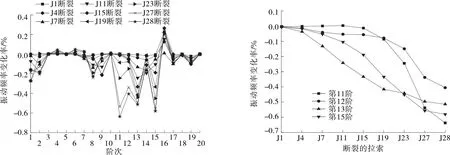
圖4 3#塔中跨單根拉索斷裂工況下斜拉橋的振動頻率變化

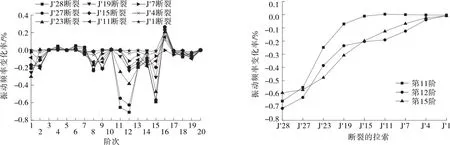
圖5 4#塔邊跨單根拉索斷裂工況下斜拉橋的振動頻率變化

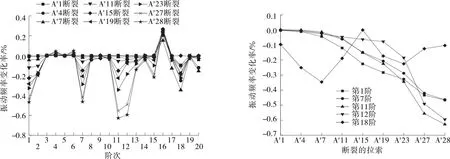
圖6 4#塔中跨單根拉索斷裂工況下斜拉橋的振動頻率變化

由圖3～6可知:邊跨發生拉索斷裂,該橋第1階、第7階、第11～12階振動頻率變化較明顯,變化率大于0.3%;中跨發生拉索斷裂,第11～12階、第15階振動頻率變化較明顯,變化率大于0.3%;拉索斷裂對第3～6階、第10階、第19階振動頻率幾乎沒有影響。整體來說,拉索斷裂后該橋的振動頻率減小。長索端發生拉索斷裂,橋梁動力特性變化尤其明顯,相鄰拉索發生斷裂,振動頻率變化率相差較大;短索端拉索斷裂,橋梁動力特性幾乎不發生變化。

5 結論

(1) 二期恒載變化對斜拉橋動力特性的影響很小,第3～6階振動頻率幾乎不受二期恒載變化的影響。二期恒載變化對斜拉橋動力特性的影響可不予考慮。

(2) 拉索損傷對斜拉橋動力特性的影響較大,最大振動頻率變化率為3.95%;拉索損傷程度越大,振動頻率越小;振動頻率變化率越大,對動力特性的影響越大;拉索有效截面積的改變對振動頻率的影響最突出。

(3) 單根拉索斷裂對斜拉橋動力特性的影響較小,其中長索斷裂時動力特性變化較明顯,短索斷裂時動力特性變化很小。拉索斷裂主要考慮長索發生斷裂的情況,以中跨長索發生斷裂對動力特性的影響最明顯。