基于粒子-人工蜂群算法的3RPUPc-UPS并聯(lián)機(jī)構(gòu)運(yùn)動(dòng)學(xué)正解研究*

常振振,張彥斌,張 雙,宋黎明,李耀光

(河南科技大學(xué) 機(jī)電工程學(xué)院,河南 洛陽(yáng) 471003)

0 引 言

并聯(lián)機(jī)構(gòu)具有精度高、累計(jì)誤差小、承載能力強(qiáng)、結(jié)構(gòu)緊湊等特點(diǎn)[1-4],已被廣泛應(yīng)用于醫(yī)療康復(fù)、航空航天、工業(yè)生產(chǎn)等領(lǐng)域。但并聯(lián)機(jī)構(gòu)具有強(qiáng)運(yùn)動(dòng)耦合性,導(dǎo)致其運(yùn)動(dòng)學(xué)求解十分困難,阻礙了并聯(lián)機(jī)構(gòu)的推廣應(yīng)用。

運(yùn)動(dòng)學(xué)分析包括運(yùn)動(dòng)學(xué)逆解和運(yùn)動(dòng)學(xué)正解分析,是機(jī)構(gòu)結(jié)構(gòu)優(yōu)化、性能分析和精確控制等理論研究的基礎(chǔ)。相比于運(yùn)動(dòng)學(xué)逆解,并聯(lián)機(jī)構(gòu)的正解計(jì)算更為復(fù)雜,其求解方法包括解析法和數(shù)值法。常用的解析法有幾何法[5-6]、矢量代數(shù)法[7]和四元數(shù)法[8]等,數(shù)值法有不動(dòng)點(diǎn)迭代法和牛頓迭代法等[9]。

NAZARI A A等人[10]根據(jù)機(jī)構(gòu)的幾何特征,將機(jī)構(gòu)的空間表達(dá)轉(zhuǎn)化為平面表達(dá),降低了運(yùn)動(dòng)學(xué)正解方程的復(fù)雜性。陳國(guó)旺等人[11]通過(guò)結(jié)構(gòu)降耦,得到了耦合度為0的機(jī)構(gòu),并采用幾何方法求解了其位置正解的顯式表達(dá)。

解析法雖能求取全部運(yùn)動(dòng)學(xué)正解,但對(duì)耦合度高的機(jī)構(gòu),其數(shù)學(xué)推導(dǎo)較為繁瑣。HAN Xiao-guo等人[12]采用不動(dòng)點(diǎn)迭代法分析了6SPS機(jī)構(gòu)的運(yùn)動(dòng)學(xué)正解,并證明該方法比牛頓迭代法更有優(yōu)勢(shì)。強(qiáng)紅賓等人[13]采用調(diào)整步長(zhǎng)牛頓法求解了Stewart并聯(lián)機(jī)構(gòu)的位置正解,解決了牛頓下山迭代法求解時(shí)間較長(zhǎng)的問(wèn)題。傳統(tǒng)優(yōu)化算法模型簡(jiǎn)單,但速度慢,且所求最優(yōu)解一般與初始迭代點(diǎn)有關(guān)。

近年來(lái),眾多學(xué)者將智能算法應(yīng)用于求解并聯(lián)機(jī)構(gòu)位置正解[14-17]。常用方法有神經(jīng)網(wǎng)絡(luò)法(neural network,NN)[18]、遺傳算法(genetic algorithm,GA)[19]、粒子群算法[20]等。NN算法性能好,但需要大量的訓(xùn)練樣本;GA算法具有可擴(kuò)展性,容易與其他算法結(jié)合,但收斂速度慢、局部搜索能力差;PSO算法收斂速度快,但全局尋優(yōu)性差,容易陷入局部最優(yōu)解。

人工蜂群算法[21]是一種模擬自然界蜂群行為的優(yōu)化算法。該算法參數(shù)設(shè)置少,對(duì)于連續(xù)函數(shù)的全局優(yōu)化具有很好的搜索特性;但其后期收斂速度慢。

筆者針對(duì)新型3RPUPc-UPS并聯(lián)機(jī)構(gòu)的運(yùn)動(dòng)學(xué)特性進(jìn)行研究,根據(jù)機(jī)構(gòu)幾何特征建立位置逆解方程,并構(gòu)建出位置正解求解模型;進(jìn)而提出一種基于粒子-人工蜂群算法的并聯(lián)機(jī)構(gòu)運(yùn)動(dòng)學(xué)求解方法;利用MATLAB的GUI模塊開發(fā)機(jī)構(gòu)運(yùn)動(dòng)學(xué)正解求解軟件,利用算例分析,驗(yàn)證該算法的有效性。

1 機(jī)構(gòu)的運(yùn)動(dòng)特性分析

1.1 機(jī)構(gòu)的結(jié)構(gòu)設(shè)計(jì)

新型3RPUPc-UPS并聯(lián)機(jī)構(gòu)的結(jié)構(gòu)簡(jiǎn)圖如圖1所示。

圖1 3RPUPc-UPS并聯(lián)機(jī)構(gòu)結(jié)構(gòu)簡(jiǎn)圖

由圖1可知:動(dòng)平臺(tái)與定平臺(tái)之間通過(guò)兩種不同結(jié)構(gòu)類型的支鏈連接。第一種支鏈結(jié)構(gòu)類型為RPUPc(Li,i=1～3),由轉(zhuǎn)動(dòng)副Ri、移動(dòng)副Pi、萬(wàn)向鉸Ui和環(huán)形移動(dòng)副Pci依次串聯(lián)組成,并由Pci副和Ri副分別與動(dòng)平臺(tái)、定平臺(tái)相連。

為方便表述,可以將Ui副用兩個(gè)垂直相交的轉(zhuǎn)動(dòng)副Ri1和Ri2代替。其中,Ri副的軸線與Ri1副的軸線相互平行,并垂直于Pi副的移動(dòng)方向;Ri2副的軸線在動(dòng)平臺(tái)平面內(nèi)指向動(dòng)平臺(tái)圓心點(diǎn)Q,并與Pci副的移動(dòng)方向垂直。Pci副與Ui副始終位于動(dòng)平臺(tái)平面內(nèi)。

第二種支鏈結(jié)構(gòu)類型為UPS(L4),由萬(wàn)向鉸U4、移動(dòng)副P4和球副S依次串聯(lián)組成。將U4副用兩個(gè)軸線垂直相交的轉(zhuǎn)動(dòng)副R41和R42表示,S副用三個(gè)軸線交于一點(diǎn)并兩兩垂直的轉(zhuǎn)動(dòng)副RS41、RS42和RS43表示。R41副的軸線垂直于定平臺(tái)平面,R42副的軸線與RS41副的軸線分別垂直于P4副的移動(dòng)方向,RS42副的軸線在動(dòng)平臺(tái)內(nèi)并指向點(diǎn)Q。

Ri副與U4副均勻分布在圓心點(diǎn)為O,半徑為R的圓OR上,Ri副軸線與圓OR相切,且R2副軸線與R1副和R3副軸線垂直。初始位置時(shí),R2副軸線與R42副軸線平行。

1.2 機(jī)構(gòu)的自由度與耦合度分析

1.2.1 自由度計(jì)算

第一種結(jié)構(gòu)類型的運(yùn)動(dòng)支鏈拓?fù)浣Y(jié)構(gòu)記為{-Ri(⊥Pi)//Ri1(⊥Ri2)//Pci-},第二種結(jié)構(gòu)類型則記為{-R41⊥R42(⊥P4)//RS41⊥RS42⊥RS43}。由于Pci副的作用效果可等效為一個(gè)轉(zhuǎn)動(dòng)軸與動(dòng)平臺(tái)中心線重合的轉(zhuǎn)動(dòng)副Rci,所以這兩種類型支鏈末端構(gòu)件的方位特征集[22]17-28(position and orientation characteristics,POC)分別為:

(1)

(2)

基于方位特征方程求解并聯(lián)機(jī)構(gòu)的自由度公式為:

(3)

由第1、2條支鏈構(gòu)成第一個(gè)獨(dú)立回路,可得:

(4)

而第1、2條支鏈構(gòu)成的子并聯(lián)機(jī)構(gòu)PM1的POC集為:

(5)

PM1與第3條分支構(gòu)成第2個(gè)回路,則有:

(6)

那么,子并聯(lián)機(jī)構(gòu)PM2的POC集為:

(7)

同理,PM2與支鏈4構(gòu)成第3個(gè)回路,則:

(8)

因此,并聯(lián)機(jī)構(gòu)的自由度和POC集分別為:

(9)

(10)

式(9)和式(10)表明:選取移動(dòng)副Pi(i=1～3)的線位移和U4副中R41的轉(zhuǎn)軸角位移為機(jī)構(gòu)的主動(dòng)輸入時(shí),該機(jī)構(gòu)為四自由度三轉(zhuǎn)動(dòng)一移動(dòng)并聯(lián)機(jī)構(gòu),對(duì)應(yīng)于人體腕關(guān)節(jié)掌屈/背伸、橈偏/尺偏、旋前/旋后和沿手臂方向的拉伸四種康復(fù)訓(xùn)練動(dòng)作,可將其應(yīng)用于腕關(guān)節(jié)康復(fù)訓(xùn)練機(jī)構(gòu)。

1.2.2 耦合度計(jì)算

由基于序單開鏈(single open chain,SOC)的機(jī)構(gòu)組成原理可知[22]107-115,任一機(jī)構(gòu)可分解為若干基本運(yùn)動(dòng)鏈,獨(dú)立回路數(shù)為v的基本運(yùn)動(dòng)鏈可分解為v個(gè)有序單開鏈SOCi(i=1～v),其中,第j個(gè)SOCj的約束度定義為:

(11)

式中:gj為第j個(gè)SOCj的運(yùn)動(dòng)副數(shù);Ij為第j個(gè)SOCj的驅(qū)動(dòng)副數(shù)。

機(jī)構(gòu)的耦合度定義為[23]:

(12)

3RPUPc-UPS機(jī)構(gòu)各有序單開鏈的約束度分別為:

(13)

(14)

(15)

將式(13)～式(15)代入式(12),得:

(16)

式(16)表明:該機(jī)構(gòu)的耦合度為2,建立其正解解析式十分復(fù)雜[24],而求取其數(shù)值解則相對(duì)簡(jiǎn)單。

由于運(yùn)動(dòng)學(xué)逆解方程是構(gòu)建數(shù)值解模型的理論基礎(chǔ),因此,需要先進(jìn)行機(jī)構(gòu)的逆解建模分析。

2 機(jī)構(gòu)的運(yùn)動(dòng)學(xué)逆解分析

設(shè)Ai點(diǎn)為環(huán)形移動(dòng)副Pci的中心點(diǎn),Ci點(diǎn)為Ui(i=1～3)副和S副的中心點(diǎn)。在動(dòng)平臺(tái)平面內(nèi),Ai點(diǎn)與Ci點(diǎn)分別在半徑為r的圓Qr和半徑為c的圓Qc上。Bi點(diǎn)為Ri副和U4副的中心點(diǎn)。

筆者以定平臺(tái)幾何中心點(diǎn)O為原點(diǎn),建立坐標(biāo)系O-XYZ,其中,X軸與OB3重合并指向B3點(diǎn),Y軸與OB4重合并指向B4點(diǎn),Z軸垂直定平臺(tái)平面向上。坐標(biāo)系Q-xyz的坐標(biāo)原點(diǎn)Q位于動(dòng)平臺(tái)幾何中心,y軸與QC4重合并指向C4點(diǎn),z軸垂直于動(dòng)平臺(tái)平面向上,x軸由右手法則確定。

2.1 逆解模型的建立

設(shè)CiBi的長(zhǎng)度為li,即前3條支鏈的驅(qū)動(dòng)桿長(zhǎng)度,δ表示轉(zhuǎn)軸R41的角位移(見圖1),則并聯(lián)機(jī)構(gòu)的運(yùn)動(dòng)學(xué)逆解為已知?jiǎng)悠脚_(tái)的位姿參數(shù)α、β、γ和z,需要求解機(jī)構(gòu)主動(dòng)輸入線位移li和輸入角位移δ。

動(dòng)平臺(tái)相對(duì)定平臺(tái)的姿態(tài)變換矩陣可表示為:

R=Rx(α)Ry(β)Rz(γ)=

(17)

式中:Rx(α),Ry(β),Rz(γ)為動(dòng)平臺(tái)繞x、y和z軸的坐標(biāo)變換矩陣;c*=cos*,s*=sin*。

設(shè)圓Qc上任一點(diǎn)CQ在xQy平面內(nèi)的坐標(biāo)為(x,y,0),則圓Qc在xQy平面內(nèi)的方程為:

x2+y2=c2

(18)

點(diǎn)CQ在坐標(biāo)系O-XYZ下的坐標(biāo)向量CO為:

CO=RCQ+Q

(19)

式中:CQ為點(diǎn)CQ在Q-xyz中的坐標(biāo)向量;Q為點(diǎn)Q在O-XYZ中的坐標(biāo)向量(0,0,z)。

由于動(dòng)平臺(tái)繞z軸的轉(zhuǎn)動(dòng)不影響圓Qc在XOY平面投影的形狀,將γ=0代入式(19),求點(diǎn)CQ在XOY平面上的投影坐標(biāo)(xO,yO)為:

(20)

將式(20)代入式(18),可得圓Qc在XOY平面上投影的解析式為:

(21)

式中:t*=tan*。

(22)

(23)

設(shè)θi(i=1～3)為QCi與水平面的夾角,易知θ2=α,θ1=θ3。θ3的瞬時(shí)位形圖如圖2所示。

圖2 θ3瞬時(shí)位形

若令θ1=θ3=θ,則:

(24)

根據(jù)分支伸縮桿的幾何約束條件可得:

(25)

(26)

(27)

而由式(19)可計(jì)算出點(diǎn)C4(0,c,0)在定坐標(biāo)系O-XYZ下的坐標(biāo),即:

(28)

(29)

可計(jì)算得:

(30)

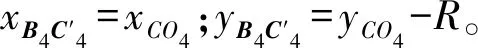
2.2 逆解驗(yàn)證

筆者給定結(jié)構(gòu)尺寸參數(shù)c=60 mm、R=120 mm,根據(jù)式(25)～式(27)、式(30),利用MATLAB對(duì)機(jī)構(gòu)逆解進(jìn)行數(shù)值仿真,并繪制各分支主動(dòng)關(guān)節(jié)的運(yùn)動(dòng)曲線,用虛線表示;同時(shí),利用SOLIDWORKS進(jìn)行虛擬樣機(jī)建模和運(yùn)動(dòng)學(xué)逆解仿真,并用點(diǎn)畫線表示。各軟件的仿真曲線為4條,仿真時(shí)間t為20 s。

仿真結(jié)果如圖3所示。

圖3 逆解仿真曲線

圖3中,對(duì)比兩種不同軟件做出的運(yùn)動(dòng)仿真曲線可知:每?jī)蓷l曲線重合,表明仿真結(jié)果一致,驗(yàn)證了機(jī)構(gòu)逆解理論分析的正確性。

3 基于P-ABC算法的正解分析

3.1 機(jī)構(gòu)運(yùn)動(dòng)學(xué)正解模型

由于直接建立機(jī)構(gòu)運(yùn)動(dòng)學(xué)正解的解析方程比較困難,因此,筆者根據(jù)機(jī)構(gòu)主動(dòng)輸入線位移li和角位移δ(用l4表示δ),求解同時(shí)滿足逆解方程式(25)～式(27)和式(30)的α、β、γ和z的值,以達(dá)到運(yùn)動(dòng)學(xué)正解的數(shù)值求解目的。

機(jī)構(gòu)的逆解方程可進(jìn)一步改寫為:

li-fi(α,β,γ,z)=0(i=1～4)

(31)

筆者將式(31)轉(zhuǎn)化為帶約束的多目標(biāo)非線性方程最小化問(wèn)題,建立機(jī)構(gòu)正解的求解模型,即:

(32)

(33)

式中:fPS為算法的適應(yīng)度,表示總體誤差,其值越小,求解精度越高。

3.2 粒子-人工蜂群算法的構(gòu)建

在實(shí)際應(yīng)用中,并聯(lián)機(jī)構(gòu)快速準(zhǔn)確的控制效果取決于運(yùn)動(dòng)學(xué)正解的求解精度和響應(yīng)時(shí)間。筆者融合ABC與PSO算法,提出了一種基于P-ABC算法的并聯(lián)機(jī)構(gòu)運(yùn)動(dòng)學(xué)正解求解方法。

3.2.1 ABC算法

ABC算法來(lái)源于自然界蜜蜂尋找蜜源采蜜的過(guò)程,如圖4所示。

圖4 蜜蜂采蜜過(guò)程

算法模型包括蜜源、引領(lǐng)蜂、觀察蜂和偵察蜂。引領(lǐng)蜂發(fā)現(xiàn)蜜源后返回蜂巢,在舞蹈區(qū)內(nèi)與觀察蜂交流蜜源信息,并以一定概率雇傭觀察蜂探索當(dāng)前蜜源或被雇傭去探索其他蜜源,概率由蜜源的質(zhì)量決定。若當(dāng)前蜜源被探索完畢,引領(lǐng)蜂將放棄當(dāng)前蜜源并轉(zhuǎn)化為偵察蜂,以偵察蜂巢附近的新蜜源。

3.2.2 PSO算法

PSO算法來(lái)源于對(duì)鳥群覓食行為的研究,并將鳥群中的個(gè)體簡(jiǎn)化為具有位置和速度的粒子。

鳥類覓食的過(guò)程如圖5所示。

圖5 鳥類覓食過(guò)程

鳥類覓食的方向受兩個(gè)因素的影響,一是自己曾經(jīng)發(fā)現(xiàn)最多食物的地方Pp,二是在交流中獲得的其他個(gè)體發(fā)現(xiàn)最多食物的地方Pg,最終在兩者之間選擇一個(gè)新方向。

3.2.3 P-ABC算法

PSO算法迭代速度快,但缺乏速度的動(dòng)態(tài)調(diào)節(jié),容易陷入局部最優(yōu),導(dǎo)致收斂精度低和不易收斂,其結(jié)果受到算法參數(shù)的影響。ABC算法雖迭代速度較慢,但每次迭代過(guò)程中都會(huì)進(jìn)行全局和局部的最優(yōu)解搜索,尋找最優(yōu)解的概率高。

為提高求解并聯(lián)機(jī)構(gòu)正解的速度和精度,筆者提出P-ABC算法,其可以有效克服PSO算法易陷入局部最優(yōu)解、求解精度低、ABC算法求解時(shí)間長(zhǎng)的缺陷。相比于同類研究[25],其參數(shù)設(shè)置更為簡(jiǎn)單,計(jì)算量也更小。

在該算法中,蜜源和Pp對(duì)應(yīng)優(yōu)化問(wèn)題中的可能解,其數(shù)量分別與引領(lǐng)蜂和粒子的數(shù)量相同,且一一對(duì)應(yīng)。P-ABC算法包含兩個(gè)階段,每個(gè)階段都以獲取fPS最小值為正解計(jì)算結(jié)果的選擇依據(jù)。

首先,在PSO算法中,在有N個(gè)粒子的D維搜索空間內(nèi),第i個(gè)粒子的位置和速度更新公式分別為:

(34)

(35)

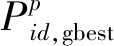
(36)

式中:xi,j為第i個(gè)蜜源的第j維值,i=1～N。

觀察蜂在舞蹈區(qū)內(nèi)獲取全部引領(lǐng)蜂的蜜源信息,并采用輪盤賭的方式選擇新蜜源,其選擇概率為:

(37)

其中,fitMi為第i個(gè)蜜源的適應(yīng)度,其表達(dá)式為:

(38)

引領(lǐng)蜂在舞蹈區(qū)進(jìn)行蜜源信息交流后,獲得新的蜜源為:

(39)

式中:φi,j為區(qū)間[-1,1]的隨機(jī)數(shù)。

引領(lǐng)蜂變成偵察蜂后,根據(jù)下式獲取新蜜源:

(40)

每只蜜蜂可通過(guò)貪婪法比較新舊蜜源的適應(yīng)度f(wàn)PS,并選擇優(yōu)勢(shì)解作為新蜜源。算法完成設(shè)定迭代次數(shù)后,最小適應(yīng)度f(wàn)PS對(duì)應(yīng)的蜜源為所求最優(yōu)解。

3.3 算例分析

筆者分別利用ABC、PSO和P-ABC算法對(duì)3RPUPc-UPS并聯(lián)機(jī)構(gòu)的運(yùn)動(dòng)學(xué)正解進(jìn)行數(shù)值求解,以驗(yàn)證P-ABC算法的優(yōu)越性。

假定對(duì)三種算法設(shè)置相同的迭代次數(shù),p值為總迭代次數(shù)的二分之一,其余算法參數(shù)選取常用數(shù)值。

為方便運(yùn)算和比較三種算法的性能,筆者使用MATLAB中的GUI模塊開發(fā)出基于三種算法的機(jī)構(gòu)正解求解軟件,其界面如圖6所示。

圖6 軟件初始界面

以求解動(dòng)平臺(tái)位姿α=25°、β=34°、γ=23°、z=360 mm的正解為例,設(shè)機(jī)構(gòu)的結(jié)構(gòu)參數(shù)R=120 mm、c=60 mm;最大迭代次數(shù)取300,群體個(gè)數(shù)取100,ω=0.8,c1=c2=2;以及運(yùn)動(dòng)學(xué)逆解的計(jì)算結(jié)果,l1=332.048 mm、l2=390.904 mm、l3=402.294 mm和l4=-14.438 9°。

筆者將所有參數(shù)分別輸入到軟件界面相應(yīng)的輸入框內(nèi),點(diǎn)擊正解計(jì)算,可得到三種算法的運(yùn)行時(shí)間、求解誤差、適應(yīng)度值和適應(yīng)度曲線,最后點(diǎn)擊下載即可保存該位姿下的適應(yīng)度曲線,如圖7所示。

圖7 適應(yīng)度曲線

由圖7可知:前150次迭代中,ABC算法收斂速度快于PSO和P-ABC算法的速度;150次迭代之后,ABC算法適應(yīng)度曲線處于穩(wěn)定狀態(tài),PSO算法處于緩慢收斂狀態(tài),而P-ABC算法加速收斂,并偏離PSO算法;在300次迭代終止時(shí),P-ABC算法適應(yīng)度值遠(yuǎn)小于ABC和PSO算法的值,該算法克服了ABC算法迭代中止和PSO算法求解精度低的缺陷。

軟件獨(dú)立運(yùn)行30次后的誤差均值如表1所示。

表1 算法獨(dú)立運(yùn)行30次的誤差均值

從表1可知:相比于ABC算法,P-ABC算法運(yùn)行時(shí)間縮短了50.02%,整體誤差等級(jí)從10-18變?yōu)?0-20;相比于PSO算法,其運(yùn)行時(shí)間雖長(zhǎng),但誤差等級(jí)從10-10降至10-20,降低了10個(gè)數(shù)量級(jí)。

為驗(yàn)證P-ABC算法的適用性,筆者選取50組不同位姿進(jìn)行300次迭代正解求解運(yùn)算,其中5組的計(jì)算結(jié)果如表2所示。

表2 P-ABC算法不同位姿下的運(yùn)算結(jié)果

表2計(jì)算結(jié)果表明:P-ABC算法單次求解時(shí)間在0.5 s內(nèi),求解誤差級(jí)別為10-20,能有效滿足實(shí)際應(yīng)用。

4 結(jié)束語(yǔ)

針對(duì)3RPUPc-UPS并聯(lián)機(jī)構(gòu)運(yùn)動(dòng)學(xué)正解求解困難的問(wèn)題,筆者分析了3RPUPc-UPS并聯(lián)機(jī)構(gòu)的運(yùn)動(dòng)輸出特性,并融合了PSO和ABC算法,提出了兼顧兩者優(yōu)點(diǎn)的P-ABC算法。

研究結(jié)論如下:

1)分析了機(jī)構(gòu)的拓?fù)浣Y(jié)構(gòu)和方位特征集,計(jì)算得出其自由度為4,運(yùn)動(dòng)耦合度為2,表明機(jī)構(gòu)具有較強(qiáng)的運(yùn)動(dòng)學(xué)耦合性;

2)利用機(jī)構(gòu)幾何特征建立了機(jī)構(gòu)運(yùn)動(dòng)學(xué)逆解方程,推導(dǎo)出其解析表達(dá)式,并利用MATLAB和SOLIDWORKS軟件仿真驗(yàn)證了逆解模型的正確性;

3)建立了機(jī)構(gòu)運(yùn)動(dòng)學(xué)正解的數(shù)值求解模型,將運(yùn)動(dòng)學(xué)正解求解轉(zhuǎn)化為含有約束的多目標(biāo)非線性方程的最小化問(wèn)題。算例分析結(jié)果表明,P-ABC算法不僅運(yùn)算快、運(yùn)行時(shí)間短,還具有求解精度高的優(yōu)點(diǎn)。相對(duì)于ABC算法,P-ABC算法的運(yùn)行時(shí)間縮短了50.02%;相對(duì)于POS算法,其求解精度提高了10個(gè)數(shù)量級(jí)。

在后續(xù)的研究工作中,筆者將對(duì)該算法參數(shù)進(jìn)行優(yōu)選,以獲取最佳的工作性能,并將其應(yīng)用于其他類型機(jī)構(gòu)的運(yùn)動(dòng)學(xué)求解中,以驗(yàn)證該算法的通用性。