關于“利用手機Phyphox軟件探究向心加速度公式”實驗的再思考
張明碩 黃致新
(華中師范大學物理科學與技術學院 湖北 武漢 430079)
智能手機的普及促進了手機傳感器在物理教學中的應用,在向心加速度的教學中,學生可以利用手機的加速度傳感器和陀螺儀分別測出圓周運動物體的向心加速度和角速度的大小,并通過Phyphox軟件將數據可視化并以XLS等表格格式導出,對數據進行分析可以有效得出向心加速度公式.
為了挖掘出“利用手機Phyphox軟件探究向心加速度公式”這一實驗更加豐富的教學功能,讓此實驗更好地應用于中學教學中,筆者結合具體實驗與相關文獻對其進行再思考,并就相關問題做進一步闡釋與澄清.
1 實驗驗證和探究的邏輯
為了找出向心加速度、轉動半徑、角速度三者的關系,探究或驗證向心加速度公式,我們一般會用到控制變量法對所需數據進行測量[1-3]:控制轉動半徑r大小不變,改變角速度ω大小,測得相應的向心加速度a,得出a-ω關系為a=k1ω2;同理,控制ω一定,得出a-r關系為a=k2r;然后從a=k1ω2和a=k2r推導出向心加速公式為a=rω2.
關于上述推導過程,筆者認為需要對其中的邏輯做進一步論述.根據a=k1ω2和a=k2r如何推導出a=rω2,以及推導過程所體現的邏輯是對公式a=rω2的驗證還是探究呢?
1.1 對公式進行“驗證”
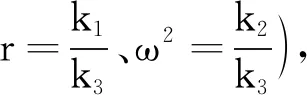
1.2 對公式進行“探究”
在未知向心加速度公式的情況下,從邏輯上講,a=k1ω2和a=k2r還不足以推斷出公式a=rω2,因為k1和k2為什么不可能是某個還未探討的物理量呢?但是從物理學研究的一般過程而言,物理學的探究也需要基于事實和有所根據的猜想,從a=k1ω2和a=k2r是可以猜想出公式a=rω2的.在教學中需要引導學生對斜率值進行觀察,發現a-ω2(a-r)圖像的斜率值與轉動半徑(角速度的平方)的大小在誤差允許范圍內相等,即k1=r、k2=ω2,環環相扣,進而順利猜想出a=rω2,再利用多組數據重復檢驗,最終確認向心加速度公式為a=rω2.這樣即強調了物理核心素養“科學探究”中的證據要素[4],又能讓學生從問題到猜想再到驗證,最終得出結論,加深學生對物理學研究過程的理解.
2 傳感器位置的確定方法
本文實驗需要用到手機中的加速度傳感器和陀螺儀.陀螺儀的位置難以確定,因為在同一轉速下,手機上任何地方的角速度大小均相等,換言之,陀螺儀的位置并不會對角速度的測量值產生影響.但是,手機上不同位置的加速度大小是不相等的,這使得確認加速度傳感器的位置成為必要.
筆者按圖1所示對器材進行組裝,將手機水平放置在圓盤上進行實驗,設計了兩種確認加速度傳感器位置的方法.

圖1 器材組裝圖
2.1 弧線相交法
如圖2所示,為弧線相交法找到的手機加速度傳感器位置.具體操作如下.
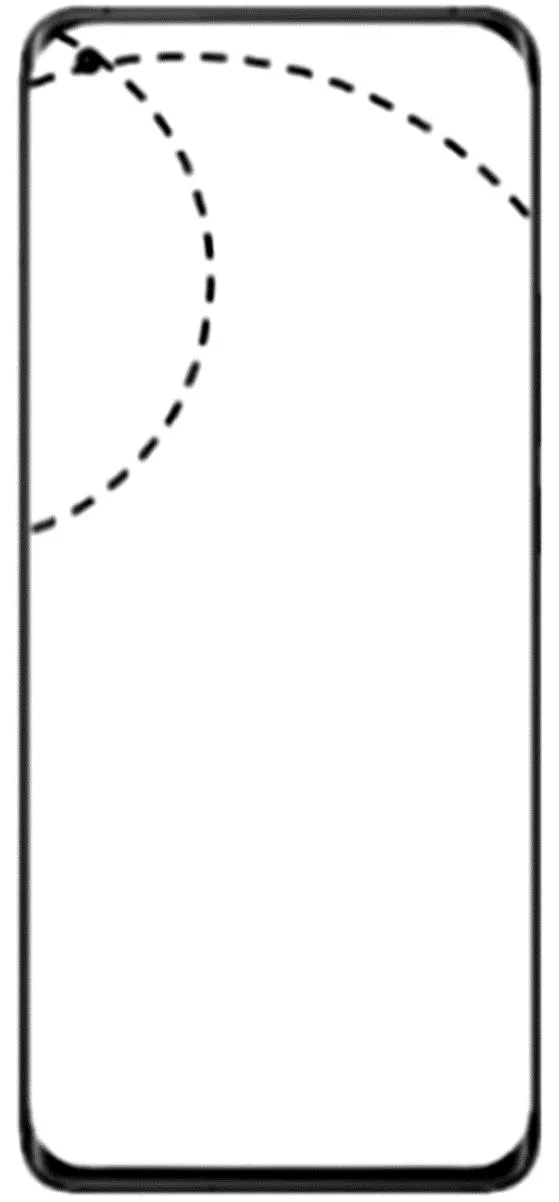
圖2 弧線相交法
將手機任意擺放在某一位置,改變角速度,繪制a-ω2圖像.圖像擬合出的斜率值,即為轉動半徑大小,也就是加速度傳感器到圓心的距離,記為r1,圍繞圓心以r1為半徑畫圓在手機上留下一段弧線;改變手機位置,重復操作,以r2為半徑在手機上留下另一段弧線;兩段弧線的交點即為加速度傳感器的位置.
由于長度測量工具的精度限制和人為操作的誤差,筆者只能大致確認實驗所用手機的加速度傳感器位置在前置攝像頭附近.
2.2 直線相交法
為了導出向心加速度大小的測量值,筆者和文獻中的實驗設計用到的多為圖3所示的“向心加速度”模塊.跳出思維定勢,向心加速度本質上仍然是加速度,我們不妨利用圖4所示原始傳感器中的“加速度(不含g)”模塊導出相關數據.

圖3 “向心加速度”模塊

圖4 “加速度(不含g)”模塊
“加速度(不含g)”模塊可以顯示x、y、z軸3個方向的分加速度以及合加速度的大小,手機的x、y、z軸如圖5所示.將手機平放在水平圓盤上轉動,忽略z軸方向的加速度,只考慮x軸與y軸方向的加速度.

圖5 Phyphox手機坐標系
實驗時任意擺放手機使其做勻速圓周運動,向心加速度為x軸與y軸兩個方向的加速度的矢量合成,向心加速度大小即為圖4中“加速度絕對值”的大小.
那么如何利用“加速度(不含g)”模塊確定加速度傳感器的位置呢?
我們知道,物體做勻速圓周運動時的加速度指向圓心,不存在沿切線方向的切向加速度.通過改變手機的擺放位置,使x軸方向的加速度為零(由于誤差的存在,確保x軸方向加速度值在零附近波動,平均值大致為零即可),這樣y軸指向圓心,y軸方向的加速度即為向心加速度,過圓心垂直手機x軸在手機上留下一段直線;同理,使y軸方向的加速度為零,x軸方向的加速度即為向心加速度,過圓心垂直手機y軸在手機上留下另一段直線,兩條直線的交點即為傳感器的位置.用此方法同樣確定所用手機的加速度傳感器位置在前置攝像頭附近,與“弧線相交法”得出的結果一致.
3 切向加速度對測量的影響
在文獻[1-3]中,根據控制變量法測量數據時,是讓手機做勻速圓周運動,待ω值穩定在某一數值附近時,才進行取值,并記為ω1,然后改變轉速,以同樣的方式依次得出ω2,ω3,ω4,…,根據數據繪制的a-ω圖像是一個個離散的點,每一個ω值對應的均是某次勻速圓周運動的角速度大小.因此,準確地講,文獻[1-3]利用測得的數據得出的公式a=rω2是勻速圓周運動的向心加速度公式.
那么,是否可以如勻速圓周運動一樣,對變速圓周運動的向心加速度公式進行探究呢?
文獻[5]利用Phyphox軟件探究向心加速度公式時,是從慢到快搖動自行車腳踏板,使固定在車輪上的手機做角速度不斷變大的圓周運動,測量出連續變化的角速度的值,因此得到的a-ω2圖像是一系列較為密集的點.考慮到Phyphox軟件數據采樣的時間間隔很短,我們可以將文獻[5]中a-ω2圖像近似看成是連續的.因此,文獻[5]根據數據探究的其實是變速圓周運動的向心加速度公式,得出的結論同樣為a=rω2.
從實驗結果來看,無論是變速圓周運動還是勻速圓周運動,利用各文獻所展示的數據得出的向心加速度公式均為a=rω2.
從物理意義上講,運用極限思想,變速圓周運動可以看成一系列勻速圓周運動的連續變化,所以變速圓周運動和勻速圓周運動的向心加速度公式是一致的.
但是,根據Phyphox軟件對“向心加速度”模塊的介紹,筆者發現,手機做變速圓周運動時,如何對向心加速度進行測量還需要進一步探討.
3.1 基于“向心加速度”模塊的測量
查看Phyphox軟件對“向心加速度”模塊的介紹,得知此模塊顯示的向心加速度大小其實是加速度計得到的“加速度絕對值”的大小.換言之,將手機水平放置在圓盤上進行實驗,“向心加速度”模塊顯示的加速度值其實是x軸與y軸兩個方向的分加速度經矢量合成后的合加速度的大小.
手機做勻速圓周運動時,傳感器沒有切向加速度,只有指向圓心的加速度,“向心加速度”模塊顯示的加速度值是真實的向心加速度的大小.
但是,手機做變速圓周運動時,傳感器存在切向加速度,如圖6所示.
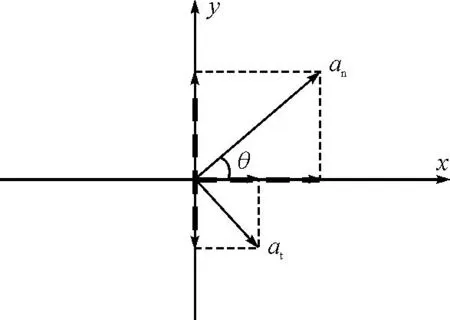
圖6 變速圓周運動的加速度
以傳感器位置為原點,建立直角坐標軸.根據
ax=ancosθ+atsinθ
和ay=ansinθ-atcosθ
不難計算出
從實驗效果來看,即使存在切向加速度,利用“向心加速度”模塊導出的數據也能很好地符合公式a=rω2.這可能是因為Phyphox軟件每次采集數據的時間間隔很短,切向加速度很小,對向心加速度大小的測量影響有限.同時,這也正好證明了“變速圓周運動是一系列勻速圓周運動的連續變化”這一物理事實.
在變速圓周運動中,切向加速度的存在會影響Phyphox軟件“向心加速度”模塊顯示的加速度值,那么是否可以消除切向加速度對向心加速度測量值的影響呢?換言之,手機做變速圓周運動時,如何顯示出真正的向心加速度?
3.2 基于“加速度(不含g)”模塊的測量
參考關于“直線相交法”的討論,我們可以通過調整手機的擺放位置,讓x軸(y軸)指向圓心,而y軸(x軸)指向圓周運動的切線方向.這樣即使是變速圓周運動,也能排除切向加速度對向心加速度測量值的影響,x軸或者y軸方向的加速度值即為向心加速度的大小.
4 結束語
利用智能手機傳感器開發的學生實驗,具有成本低、精度高等特點,將其應用于中學課堂之中,可以獲得良好的教學效果.在教師的引導下,學生能夠自主完成“利用手機Phyphox軟件探究向心加速度公式”實驗,得出向心加速度的公式.
除了完成知識的傳授、讓學生理解向心加速度公式之外,本文倡導應挖掘此實驗更加豐富的教學功能.
明晰驗證性實驗和探究性實驗的邏輯,可以培養學生對問題進行科學推理、科學論證的能力,尤其是將此實驗作為探究性實驗應用在教學中,可以讓學生對物理研究的一般過程有更加深入的理解.在探究過程中,基于證據提出猜想并嚴格地對猜想進行檢驗,明白物理學既是嚴謹的科學,同樣也是猜想的藝術.
確認加速度傳感器的位置,不僅能讓學生了解手機傳感器和Phyphox軟件工作的原理,還能讓學生對向心加速度公式進行應用,加深其對勻速圓周運動、向心加速度的方向和大小的理解,促進學生關于運動的物理觀念的構建.
討論切向加速度的存在,讓學生的認知從特殊的勻速圓周運動上升到更為一般的變速圓周運動.利用極限思想,在理論上可以認為變速圓周運動是一系列連續的勻速圓周運動的集合,但是學生不易理解變速圓周運動和勻速圓周運動的這一關系.利用手機傳感器和Phyphox軟件對變速圓周運動的向心加速度公式進行探究,得到了和勻速圓周運動一樣的結果,正好在實驗上為這一關系提供了事實證明.學生由此可以體會到物理知識在理論和實驗上的和諧統一,對實驗這一物理研究方法的理解也更為深刻.

