基于TEASER算法的空間非合作目標位姿估計

王世昌, 華寶成, 周依爾, 李小路*

1. 北京控制工程研究所 空間光電測量與感知實驗室, 北京 100094

2. 北京航空航天大學 儀器科學與光電工程學院, 北京 100191

0 引 言

在軌服務技術指一種為故障失效、燃料耗盡或者模塊更換的衛星、空間站等目標提供維修服務的技術[1]. 根據是否事先安裝可探測標記,空間目標可以分為合作目標與非合作目標[2]. 合作目標是指安裝有激光角反射器或光學標記,或者能夠主動與服務航天器通信的目標航天器. 而目前大多數在軌航天器都屬于非合作目標,它們無法與服務航天器通信,且自身結構、尺寸和運動信息完全未知或部分未知[3]. 非合作目標的相對位姿測量是未來航天器持續發展、空間交會對接的前提與重點[4].

針對非合作目標的位姿測量主要采用可見光相機作為傳感器,其測量結果直觀,相關位姿解算方法成熟. 最常見的方法是提取圖像中的特征點,再通過求解PnP問題即可得到目標位姿[5]. 但當空間光照或者目標位姿變化時,圖像容易出現過曝、模糊和失真等問題,使得特征定位不準甚至無法提取,很大程度上影響了位姿求解精度. 隨著主動式成像傳感器(如激光雷達)的快速發展,基于點云的位姿測量技術逐漸發展起來. 與可見光相機相比,激光雷達可以直接獲取目標的三維點云數據,包括空間坐標與紋理信息. 由于其主動式探測的特性使其不受光照影響,適合對目標的三維測量. 三維點云數據包含信息豐富,在空間非合作目標位姿估計方面具有獨特的優勢,是當前研究的熱點[6-9].

目前,非合作目標三維點云位姿估計已應用于火星著陸、月球車避障和交會對接等領域[10]. 2006年,TERUI等[11]采用雙目相機對左右圖像進行立體匹配從而獲取目標三維點云,并采用ICP算法將其與模型點云配準來估計目標位姿,三軸平移誤差小于1cm,旋轉誤差小于5°.2012年,RUEL等[12-13]開發的 TRIDAR系統包含了激光雷達與相機,并采用ICP算法將點云與航天器模型配準,完成相對位姿測量,用于非合作目標自主交會對接與相對導航.2016年,LIU等[14]使用Flash激光雷達獲取目標點云,進而采用ICP算法來完成位姿追蹤,在仿真實驗中平移誤差小于4 cm,旋轉誤差約為1°.2019年,LI等[15]提出了一種基于連續點云的狀態估計方法,利用擴展卡爾曼濾波估計目標的位姿參數. 最后,進行了半物理實驗研究,位置誤差小于5 cm,姿態角誤差小于3°.2020年,LI等[16]通過提取飛行時間(time of flight, TOF)相機獲取的衛星太陽翼平面點云進行粗配準,再進行ICP精配準,實現非合作衛星的位姿跟蹤,旋轉誤差小于0.1°,平移誤差小于2. 5 mm.

上述位姿估計方法大多以ICP算法為核心,但ICP的缺點是對初始值敏感. 同時,由于距離變化會使得目標點云空間離散程度不同,背景噪聲的存在也會導致點云存在誤差,不同傳感器所獲點云質量也有所不同. 上述問題都會影響最終的位姿估計結果,且不同實驗條件與算法下所得指標也無法評估. 針對點間距及噪聲變化對點云配準算法的影響,提出一種基于TEASER的位姿估計方法. 所提方法使用TEASER算法實現粗配準,可以降低誤匹配對初始位姿的影響,然后采用ICP對位姿進一步優化,實現非合作目標高精度位姿估計. TEASER算法是YANG等[17]于2021年提出的一種全局配準算法,其可以魯棒地求解含有大量外點的配準問題,使得位姿估計結果對誤匹配不敏感. 本文首先將TEASER算法與隨機采樣一致性(random sample consensus,RANSAC)算法作對比,討論點云噪聲對算法的影響,并將TEASER與ICP相結合,實現了連續幀位姿估計.

1 方 法

基于點云的位姿測量的關鍵是在已知目標三維點云的基礎上計算目標姿態,其核心問題是點云配準. 點云配準是求取兩組點集之間的旋轉與平移矩陣的過程,從配準過程而言,點云配準分為粗配準與精配準兩個過程. 粗配準是指在兩點云相對位姿完全未知的情況下對點云進行配準,主要用于兩片點云相距較遠、重合度較低的情形,可以獲得一個粗略的配準結果作為精配準的初始值. 精配準的目的是在粗配準的基礎上讓點云間的空間位置差別最小化,ICP及其變種是使用最為廣泛的算法. 基于點云的空間非合作目標位姿估計流程如圖1所示.

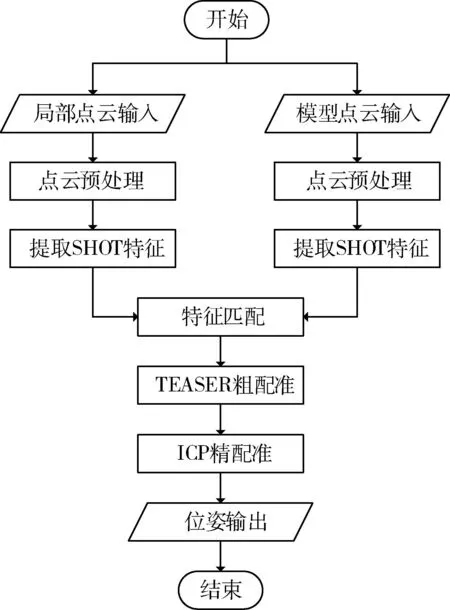
圖1 空間非合作目標位姿估計流程圖Fig.1 Flow chart of pose estimation for space non-cooperative target

首先是局部點云與模型點云讀取,對點云進行預處理,主要是為了降低計算量. 然后對預處理后點云的每一點計算SHOT,方便后續特征匹配,其過程是對于局部點云中的每一個點根據特征描述子的相似程度,找到其在模型點云中的對應點,形成匹配對.根據已有匹配對進行粗配準,得到初始變換矩陣,再將結果傳遞給精配準部分,最終得到局部點云與模型點云的位姿變換關系.

1.1 SHOT特征提取

點云特征類似于圖像特征,是對點云中某一點的鄰域幾何信息的描述或整體點云信息的描述,可以分為局部特征描述子與全局特征描述子[18].SHOT作為局部特征描述子的一種,具有旋轉及尺度不變性,容錯性較大,對于含有噪聲的點云數據有較強的魯棒性,常用于物體的位姿估計[19]. 基本思想是:對于點云中的每個查詢點,先構建點鄰域的協方差矩陣,再對協方差矩陣進行奇異值分解建立局部坐標系;以查詢點為球心,將球形鄰域按經線、緯線及徑向方向共劃分為32個子空間;計算每個子空間中的鄰域點法線與查詢點法線的夾角余弦值,再將每個子空間中的余弦值等分為11等份并進行直方圖編碼;最后將所有子空間的直方圖組合在一起,形成352維的特征描述子.

1.2 TEASER算法

現有的粗配準方法主要分為兩類:基于分支定界或點對點對應關系[20]. 基于點對點對應關系的配準方法具有更高效、穩定性更強等優點,是目前點云配準的一個標準方案. 該類算法大多是依賴基于點云局部特征描述與匹配建立的匹配對,也有一部分是基于二元或三元點對點對應關系. 而由于觀測噪聲的存在與點云結構的相似性,實際匹配中會有較多的誤匹配,如何減小誤匹配的影響成為粗配準中極其關鍵的一步.

六自由度的3D點云配準問題本質上是典型的非凸優化問題,其目標函數在六維可行域空間中具有多個波峰波谷,即優化求解過程中受初始變換矩陣影響,容易陷入局部最優解. TEASER算法將配準問題重新建模,采用半定松弛的方法求解了非線性、非凸優化問題. 假設兩組點云ai、bi之間存在尺度、平移和旋轉變換,則配準問題可以描述為

(1)

式中,s為尺度變換因子,R為旋轉變換,t為平移變換,σi為噪聲標準差. 實際匹配點對由于噪聲的存在會有許多外點,為了讓求解過程對誤匹配點對不敏感,采用截斷最小二乘(truncated least squares, TLS)為代價函數并改寫式為

(2)

如圖2所示,通過給具有較大殘差的測量值分配常數代價,最小化問題時的最優解不會出現在水平階段,從而使整個問題對外點不敏感.

圖2 截斷最小二乘估計Fig.2 Truncated least squares estimation

但是,這個問題仍是非線性最小二乘問題且非凸,窮舉搜索全局最優解的時間復雜度為O(2N).為了能在多項式時間內求解該問題,TEASER根據2個事實將式(2)分解為尺度、平移和旋轉變換3個獨立問題,并分別求解.

第一個事實是平移不變測量,即點云在平移過程中,其中任意兩點組成的向量的方向不變,如圖3所示.

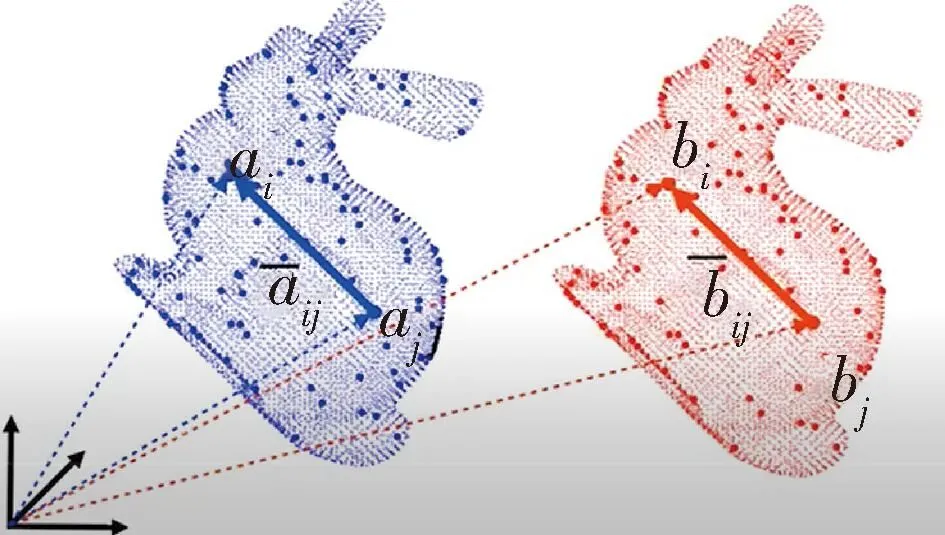
圖3 平移不變測量Fig.3 Translation invariant measurement

假設兩片待配準點云ai、bi符合以下模型:

bi=sRai+t+oi+εi

(3)

式中,εi為測量噪聲,假設噪聲服從高斯分布且有界.如果(ai,bi)構成內點,則oi為零向量,否則為任意值. 根據以上模型,令bj減去bi得

(4)

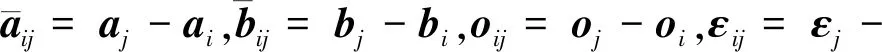
第二個事實是平移旋轉不變測量,即點云在平移與旋轉過程中,其中任意兩點組成的向量的模值不變,如圖4所示.

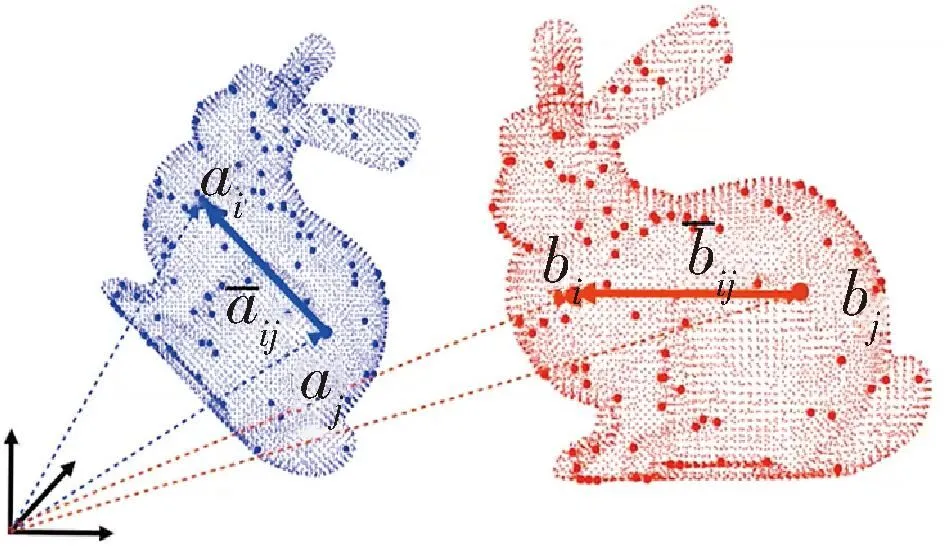
圖4 平移旋轉不變測量Fig.4 Translation and rotation invariant measurement

對式(4)取模可得

(5)

(6)

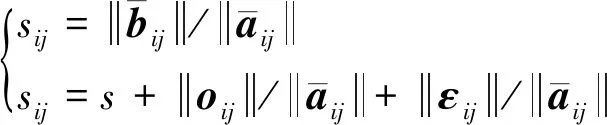
(7)

可知:利用平移旋轉不變測量后,式(3)只與尺度變換因子有關. TEASER算法需要先利用平移旋轉不變測量求出尺度變換估計值,然后根據平移不變測量與尺度變換估計值求得旋轉變換估計值,最后將尺度變換估計值與旋轉變換估計值代入式(2)即可求出平移變換估計值,從而完成基于截斷最小二乘的點云配準問題的求解.

1.3 ICP算法

ICP算法是點云配準中最為經典的精配準方法,自提出以來就受到人們的廣泛關注,后續的諸多精配準算法也是基于ICP進行改進[21]. 其基本思想是:分別在源點云與目標點云中,按照約束條件找出最近對應點,然后迭代計算變換矩陣直到誤差函數最小.

2 實驗驗證

對服務航天器來說,當其執行對接、捕獲等任務時,必然會逐漸靠近或遠離目標航天器. 由于傳感器分辨率有限,不同距離下所獲點云疏密程度不同,傳感器的觀測噪聲則會引入離群點與噪聲點,這些都會使特征提取和匹配環節出現錯誤. 如何保證配準算法對于點云分辨率變化與點云噪聲變化的魯棒性,是點云粗配準的關鍵. 為了驗證TEASER算法的魯棒性,本文將其與RANSAC算法作對比,開展不同噪聲水平與不同分辨率場景下的點云粗配準實驗,并結合ICP精配準實現精確位姿估計.

2.1 實驗描述

實驗中所用目標為北斗衛星,其長、寬和高分別為17.15 m、2.81 m和5.5 m.定義目標坐標系為:水平向右為X軸正方向,豎直向上為Y軸正方向,再根據右手準則即可確定Z軸正方向. 為了模擬不同距離、不同姿態下的目標點云,實驗中通過在Blensor仿真軟件中導入已有的模型文件,并預設目標距離虛擬相機5～15 m、姿態角為-90°～90°,共獲得15組不同位姿下的場景點云.

點云分辨率指的是點云中兩點之間的平均距離,反應了點云的密集程度,計算公式如下:

(8)

式中,n表示點云中點的數量,di表示點云中第i個點與其最近鄰點的距離.

為了獲得不同分辨率的點云,本文對原始模型點云進行了均勻降采樣,并經過隨機變換得到15組不同位姿的場景點云,每個場景均獲得8種不同分辨率的點云. 類似地,為了模擬傳感器獲得的實際場景點云中的噪聲,本文在場景點云中添加均值為0、標準差為σ=c×pr的高斯噪聲,測試點云噪聲變化對配準結果的影響. 其中c是調節因子.

為評估變換的估計值與真實值之間的差異,本文采用旋轉誤差與平移誤差兩個常用的點云配準評價指標. 對于給定的目標點云Ptgt,源點云Psrc與Ptgt之間的變換關系T可以由點云配準計算求得,Psrc與Ptgt之間的殘差變換ΔT定義為

(9)

式中,T為源點云Psrc到目標點云Ptgt變換的估計,Ttruth為二者之間的真實變換關系. 進而可求得Psrc到Ptgt的旋轉誤差erot、平移誤差etra為

(10)

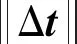
2.2 實驗結果與分析

2.2.1 點云粗配準算法評估

(1)點云分辨率變化分析

為了比較RANSAC和TEASER兩種粗配準算法對點云分辨率變化的魯棒性,本文開展了不同降采樣場景下的粗配準誤差對比實驗. 將降采樣后的場景點云與已有的模型點云進行配準,統計不同降采樣率場景的配準誤差,如圖5所示.

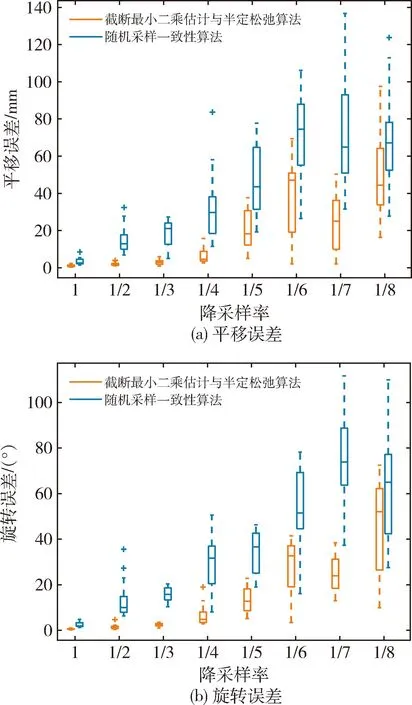
圖5 點云分辨率對粗配準的影響Fig.5 Effect of point cloud resolution on coarse registration

隨著降采樣網格半徑的增加,兩種算法的配準誤差均逐漸變大. 半徑越大,原始場景降采樣后的點云點數越少、點云分辨率越大,容易發生誤匹配. 同一降采樣網格半徑下,TEASER配準誤差的變化小于RANSAC. 當降采樣率不超過1/5時,TEASER配準誤差波動范圍更小,TEASER算法求得平移誤差最大為3.77 cm,旋轉誤差最大為22.1°,而RNASAC算法求得的平移誤差最大為8.36 cm,旋轉誤差最大為50.5°.

(2)點云噪聲變化分析

為了對比兩種算法對點云噪聲變化的魯棒性,本文通過在場景點云中添加均值為0、標準差為σ=c×pr的高斯噪聲,測試點云噪聲變化對配準結果的影響.統計不同噪聲場景下兩種算法的配準誤差,如圖6所示.

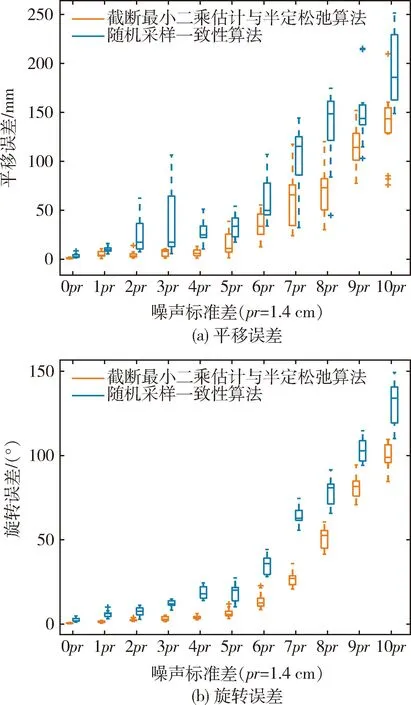
圖6 點云噪聲對粗配準影響Fig.6 Effect of point cloud noise on coarse registration

對于單一算法來說,旋轉誤差與平移誤差均隨著噪聲標準差的增加而增加. 對比不同算法在同一場景下的誤差,可以看出:噪聲一定時,采用TEASER算法求得的配準誤差總是小于RANSAC算法所求結果. 無噪聲時,TEASER的平移誤差最大為2.3 mm,旋轉誤差最大為0. 97°;當σ≤5pr時,TEASER的平移誤差最大為3. 88 cm,旋轉誤差最大為12. 1°. 噪聲標準差的增加對于TEASER算法影響較小,而RANSAC性能退化較快,這說明了TEASER比RANSAC的抗噪聲性能更好.

從以上實驗可以總結出:無論是點云分辨率還是點云噪聲變化,TEASER算法的配準結果要優于RANSAC,且在低噪聲場景下的誤差穩定性更好. 這是因為RANSAC基于窮舉搜索的思想,其假設每次選擇的隨機匹配對均是正確的,而在實際場景中,由于目標局部結構的相似性或者噪聲點的干擾會產生誤匹配,從而對求解結果造成較大影響.TEASER從配準問題的魯棒求解出發,針對配準中存在的大量外點,采用截斷最小二乘函數為代價函數,在一定程度上避免錯誤匹配對配準結果的影響.因此在面對由于環境噪聲或者點云稀疏形成的誤匹配時,TAESER算法比RANSAC算法更加魯棒.

RANSAC與TEASER兩種方法在無噪聲場景下配準結果如表1所示,可見,TEASER的配準精度優于RANSAC,運行效率也較高.

表1 無噪聲情況下RANSAC與TEASER的性能對比Tab.1 Comparison of RANSAC and TEASER without noise influencing

2.2.2 結合ICP精配準算法評估

為了進一步優化位姿估計結果,本文將TEASER粗配準結果輸入給ICP,最終得到目標精確位姿估計值,部分配準結果如圖7所示.

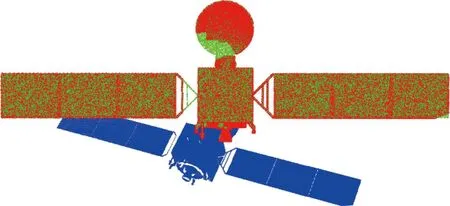
圖7 精配準(綠色為模型點云,藍色為仿真點云,紅色為配準結果)Fig.7 Fine registration (the green one is model point cloud, the blue one is simulation point cloud, and the red one is registration result)

統計不同噪聲標準差下的目標位姿估計誤差如圖8所示.從圖中分析可得:經過ICP算法優化后,位姿估計的平移與旋轉誤差均有所下降. 在無噪聲情況下,加入ICP精配準后的平移誤差小于1 mm,旋轉誤差小于0.5°;隨著高斯噪聲的加入,同一幀點云中點的位置產生變化,實際匹配對與真實對應關系相比會存在偏差,使得最終位姿估計誤差逐漸增大. 當添加的噪聲標準不超過5pr時,平移誤差最大為1.66 cm,旋轉誤差最大為2.67°,仍具有較高的精度;當噪聲繼續增加到10pr時,此時場景點云結構信息缺失,TEASER粗配準后無法提供精準初始位姿,ICP失去優化作用.

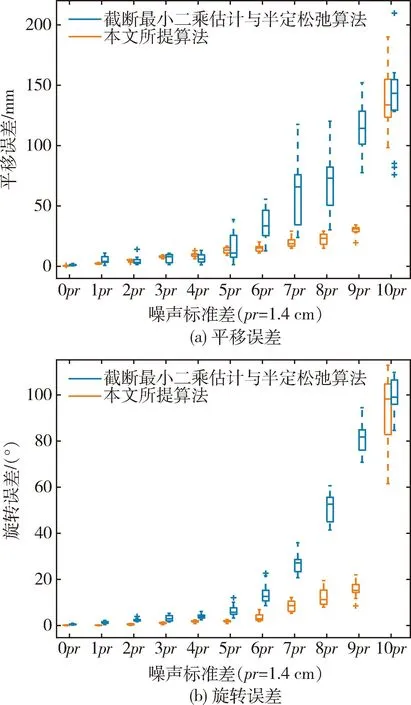
圖8 目標位姿估計誤差Fig.8 Target pose estimation errors

2.3 連續幀位姿估計

在服務航天器與目標航天器的相對運動過程中,需要不斷獲取目標位姿信息來引導自身運動. 由于相鄰時刻間運動幅度較小,目標局部點云重疊度高,因此可以直接利用ICP方法估計相鄰幀之間的運動. 為了實現目標的連續幀位姿估計,可以將整個過程分為兩部分:初始位姿估計與連續位姿估計. 以某時刻目標航天器所在位置為基準,通過將第一幀點云與已有模型點云配準即可計算出目標在服務航天器坐標系下的初始位姿,也即初始化過程. 之后,通過關聯相鄰時刻的點云數據進行位姿變換矩陣參數的傳遞,來完成航天器的運動跟蹤,最終解算出當前時刻目標航天器相對于服務航天器的絕對位姿,實現連續幀位姿估計.

隨著時間的增加,由于幀間配準誤差的不確定性,傳統ICP方法會存在累計誤差. 本文采用了周期關鍵幀配準方法,降低配準誤差隨時間增加而發生的漂移,其中本文中算法的關鍵幀為初始第一幀點云,如圖9所示. 所提算法為每隔一定周期將當前幀點云與第一幀點云配準,實現當前周期初始點云的位姿估計. 周期內的點云位姿仍基于臨幀ICP估計結果.

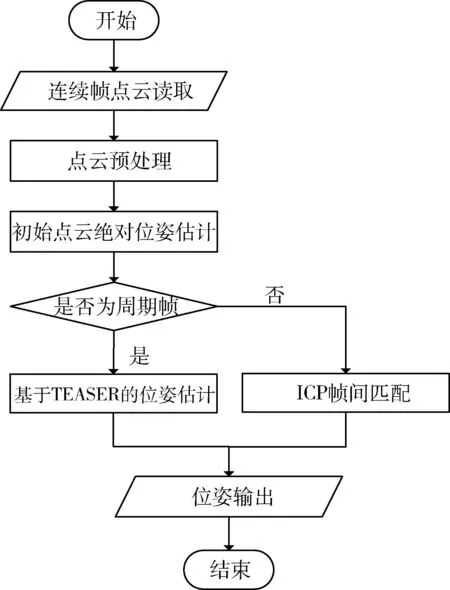
圖9 周期關鍵幀配準流程圖Fig.9 Flow chart of periodic keyframe registration

為了驗證上述方法的有效性,本文通過仿真軟件模擬目標運動過程中的連續幀點云,每隔10幀點云進行一次關鍵幀配準,實現了目標在平移與旋轉運動下的連續幀位姿估計.

(1)旋轉運動

旋轉是空間目標最常見的運動形式之一,實驗中規定目標做單軸旋轉運動. 假設目標繞其Z軸以5(°)/s的速率勻速旋轉,旋轉角從-50°～50°,虛擬相機幀率為10 Hz,則共得到201幀連續點云,部分幀點云數據如圖10所示.

圖10 部分幀點云Fig.10 Partial frame point cloud

根據仿真點云,分別采用傳統ICP幀間匹配與周期關鍵幀配準方法,解算得到每一幀點云的絕對位姿,統計估計誤差結果如圖11所示. 從兩幅圖中可以發現:隨著時間的增加,傳統ICP方法的估計誤差逐漸變大;而本文所提方法的平移誤差曲線維持在較低水平,有周期性變化趨勢. 在無噪聲情況下,所提方法平移誤差最大為1.39 cm,旋轉誤差最大為0.5°,平均平移誤差降低了85.7%,平均旋轉誤差降低了68.8%.

圖11 旋轉運動下連續幀位姿估計Fig.11 Pose estimation of continuous frames of rotation

(2)平移運動

為模擬服務航天器與目標航天器的相對平移運動過程,令目標沿其Z軸做勻速直線運動,速度為0.5 m/s,目標與相機的相對距離從20 m變至10 m,共得到201幀連續點云.同樣地,統計兩種方法計算所得每一幀目標航天器的絕對位姿估計誤差如圖12所示.

圖12 平移運動下連續幀位姿估計Fig.12 Pose estimation for continuous frames of translation

從圖中可知:傳統ICP方法所得的平移與旋轉誤差曲線均會隨時間發生漂移.在無噪聲情況下,本文所提方法的平移誤差最大為1.05 cm,旋轉誤差最大為0.1°,平均平移誤差降低了65%,平均旋轉誤差降低了89.3%.

(3)復合運動

一般情況下,平移與旋轉運動是耦合且相互影響的.為了驗證周期關鍵幀配準方法的有效性,本文開展了目標同時做平移與旋轉運動時的連續幀位姿估計實驗分析.

假設目標沿著其Z軸以0.5 m/s的速度做勻速直線運動,距相機從20 m運動至10 m,同時繞著其Y軸以5(°)/s的速率旋轉,旋轉角從-50°～50°,共獲取201幀點云.考慮到由于環境及傳感器引起的點云噪聲問題,實驗中為連續幀點云添加均值為0,標準差σ=3pr的高斯噪聲,對比傳統ICP方法與所提周期關鍵幀配準方法的位姿估計誤差結果如圖13所示.

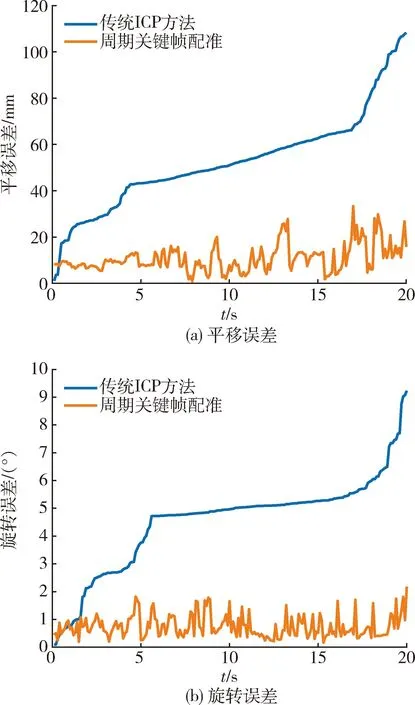
圖13 復合運動下連續幀位姿估計Fig.13 Pose estimation for continuous frames of compound motion

從圖中可以發現,隨著時間的推移,基于ICP所得的連續幀絕對位姿誤差逐漸變大,其中平移誤差最大達10.82 cm,旋轉誤差最大達9.23°.而周期關鍵幀配準方法所得的誤差曲線并未呈發散趨勢,有效減小了累計誤差,平移誤差最大為3.33 cm,旋轉誤差最大為2.18°.與傳統ICP方法相比,所提方法的平均平移誤差降低了79.6%,平均旋轉誤差降低了83.4%.平移與旋轉誤差變大是因為噪聲的加入導致了點的坐標發生偏差,導致根據特征匹配找到的對應點與真實對應點相比存在誤差,從而造成最終的求解誤差增大.實驗表明:當目標做復合運動且點云含有噪聲時,周期關鍵幀配準方法的平移與旋轉誤差變大,但仍可以有效降低傳統ICP方法的累計誤差.

實驗中同時發現,平移與復合運動連續幀位姿估計中,從第17 s開始誤差曲線有發散的跡象.為了分析這一現象的原因,利用局部點云表面積與模型點云表面積之比定義了點云局部率,并分析了連續幀點云局部率變化情況.平移運動實驗中,點云局部率從最大0.32逐步下降至0.005;而旋轉運動實驗中,點云局部率始終在0.3左右.這是因為旋轉時目標與相機間距不變,并始終保持在相機視場中;而目標發生平移時,目標與相機間距逐漸減小,目標只有部分出現在相機視場中.平移運動實驗中,當時間大于17 s時,目標點云局部率小于0.03,說明此時目標點云所含信息較少,部分結構信息缺失.在利用基于TEASER算法進行周期幀的位姿估計時,SHOT描述子計算不準確使得誤匹配增加,因此周期幀的位姿估計結果產生誤差,后續的ICP幀間匹配無法修正該誤差,故誤差曲線呈發散趨勢.

3 結 論

針對基于點云的空間非合作目標位姿估計問題,本文利用TEASER與ICP結合算法,實現目標位姿求解.同時提出一種周期關鍵幀配準方法,解決配準誤差隨時間發生漂移問題.實驗結果表明,與傳統RNASAC算法相比,采用TEASER與ICP相結合的算法實現位姿估計具有更高的精度.在連續幀位姿估計中,提出一種周期關鍵幀配準方法.與傳統ICP方法相比,所提方法的平均平移誤差與旋轉誤差均降低.其中,平移誤差小于3.33cm,旋轉誤差小于2.18°.上述方法可以為空間非合目標位姿估計提供算法理論基礎.

實際情況中,由于目標點云噪點過多使得目標幾何結構信息丟失導致誤匹配占比高,本文方法在嚴重噪聲干擾條件下仍具有提升空間.此外,本文采用傳統的最近鄰搜索尋找匹配對,效率較低.為進一步提高位姿估計的效率以及魯棒性,下一步工作將優化特征匹配環節,減少耗時,提高匹配對的準確性.